More Substitution Rule | Calculus - Mathematics PDF Download
More Substitution Rule
In order to allow these pages to be displayed on the web we’ve broken the substitution rule examples into two sections. The previous section contains the introduction to the substitution rule and some fairly basic examples. The examples in this section tend towards the slightly more difficult side. Also, we’ll not be putting quite as much explanation into the solutions here as we did in the previous section.
In the first couple of sets of problems in this section the difficulty is not with the actual integration itself, but with the set up for the integration. Most of the integrals are fairly simple and most of the substitutions are fairly simple. The problems arise in getting the integral set up properly for the substitution(s) to be done. Once you see how these are done it’s easy to see what you have to do, but the first time through these can cause problems if you aren’t on the lookout for potential problems.
Example 1: Evaluate each of the following integrals.
Ans: This first integral has two terms in it and both will require the same substitution. This means that we won’t have to do anything special to the integral. One of the more common “mistakes” here is to break the integral up and do a separate substitution on each part. This isn’t really mistake but will definitely increase the amount of work we’ll need to do. So, since both terms in the integral use the same substitution we’ll just do everything as a single integral using the following substitution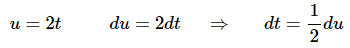
The integral is then,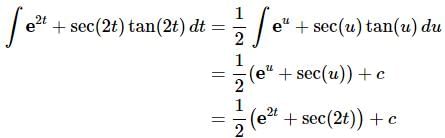
Often a substitution can be used multiple times in an integral so don’t get excited about that if it happens. Also note that since there was a 1/2 in front of the whole integral there must also be a 1/2 in front of the answer from the integral. 
Ans: This integral is similar to the previous one, but it might not look like it at first glance. Here is the substitution for this problem,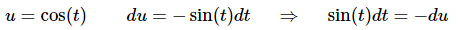
We’ll plug the substitution into the problem twice (since there are two cosines) and will only work because there is a sine multiplying everything. Without that sine in front we would not be able to use this substitution.
The integral in this case is,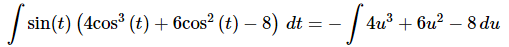
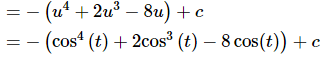
Again, be careful with the minus sign in front of the whole integral.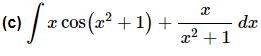
Ans: It should be fairly clear that each term in this integral will use the same substitution, but let’s rewrite things a little to make things really clear.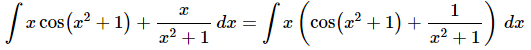
Since each term had an x in it and we’ll need that for the differential we factored that out of both terms to get it into the front. This integral is now very similar to the previous one. Here’s the substitution.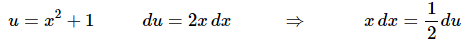
The integral is,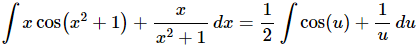
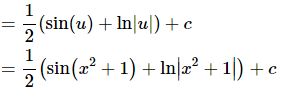
So, as we’ve seen in the previous set of examples sometimes we can use the same substitution more than once in an integral and doing so will simplify the work.
Example 2: Evaluate each of the following integrals.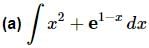
Ans: In this integral the first term does not need any substitution while the second term does need a substitution. So, to deal with that we’ll need to split the integral up as follows,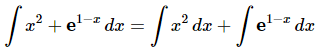
The substitution for the second integral is then,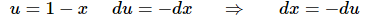
The integral is,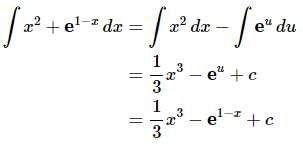
Be careful with this kind of integral. One of the more common mistakes here is do the following “shortcut”.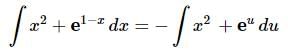
In other words, some students will try do the substitution just the second term without breaking up the integral. There are two issues with this. First, there is a “-” in front of the whole integral that shouldn’t be there. It should only be on the second term because that is the term getting the substitution. Secondly, and probably more importantly, there are xx’s in the integral and we have a dudu for the differential. We can’t mix variables like this. When we do integrals all the variables in the integrand must match the variable in the differential.
Ans: This integral looks very similar to Example 1c above, but it is different. In this integral we no longer have the xx in the numerator of the second term and that means that the substitution we’ll use for the first term will no longer work for the second term. In fact, the second term doesn’t need a substitution at all since it is just an inverse tangent.
The substitution for the first term is then,
Now let’s do the integral. Remember to first break it up into two terms before using the substitution.
In this set of examples we saw that sometimes one (or potentially more than one) term in the integrand will not require a substitution. In these cases we’ll need to break up the integral into two integrals, one involving the terms that don’t need a substitution and another with the term(s) that do need a substitution.
Example 3: Evaluate each of the following integrals.
Ans: In this integral, unlike any integrals that we’ve yet done, there are two terms and each will require a different substitution. So, to do this integral we’ll first need to split up the integral as follows,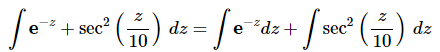
Here are the substitutions for each integral.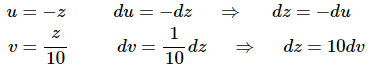
Notice that we used different letters for each substitution to avoid confusion when we go to plug back in for u and v.
Here is the integral.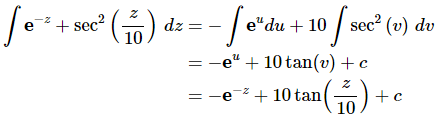
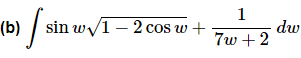
Ans: As with the last problem this integral will require two separate substitutions. Let’s first break up the integral.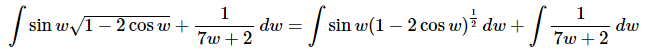
Here are the substitutions for this integral.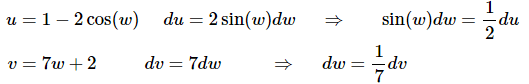
The integral is then,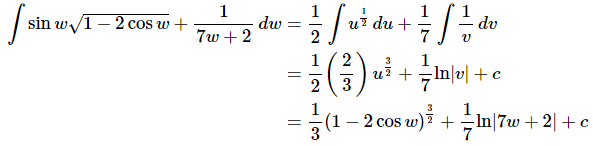
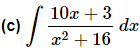
Ans: The last problem in this set can be tricky. If there was just an xx in the numerator we could do a quick substitution to get a natural logarithm. Likewise, if there wasn’t an xx in the numerator we would get an inverse tangent after a quick substitution.To get this integral into a form that we can work with we will first need to break it up as follows.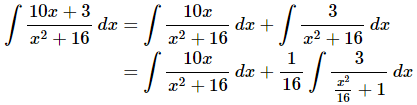
We now have two integrals each requiring a different substitution. The substitutions for each of the integrals above are,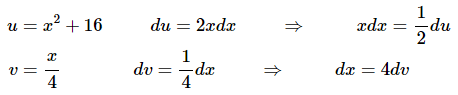
The integral is then,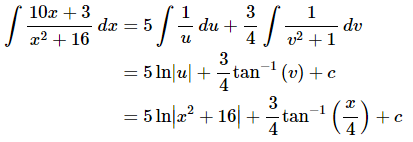
We’ve now seen a set of integrals in which we need to do more than one substitution. In these cases we will need to break up the integral into separate integrals and do separate substitutions for each.
We now need to move onto a different set of examples that can be a little tricky. Once you’ve seen how to do these they aren’t too bad but doing them for the first time can be difficult if you aren’t ready for them.
Example 4: Evaluate each of the following integrals.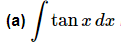
Ans: The first question about this problem is probably why is it here? Substitution rule problems generally require more than a single function. The key to this problem is to realize that there really are two functions here. All we need to do is remember the definition of tangent and we can write the integral as,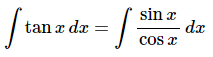
Written in this way we can see that the following substitution will work for us,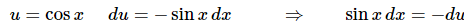
The integral is then,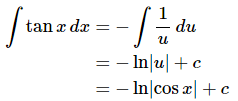
Now, while this is a perfectly serviceable answer that minus sign in front is liable to cause problems if we aren’t careful. So, let’s rewrite things a little. Recalling a property of logarithms we can move the minus sign in front to an exponent on the cosine and then do a little simplification.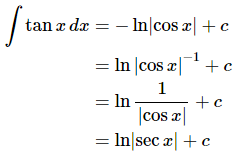
This is the formula that is typically given for the integral of tangent.
Note that we could integrate cotangent in a similar manner.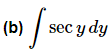
Ans: This problem also at first appears to not belong in the substitution rule problems. This is even more of a problem upon noticing that we can’t just use the definition of the secant function to write this in a form that will allow the use of the substitution rule.This problem is going to require a technique that isn’t used terribly often at this level but is a useful technique to be aware of. Sometimes we can make an integral doable by multiplying the top and bottom by a common term. This will not always work and even when it does it is not always clear what we should multiply by but when it works it is very useful.Here is how we’ll use this idea for this problem.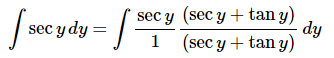
First, we will think of the secant as a fraction and then multiply the top and bottom of the fraction by the same term. It is probably not clear why one would want to do this here but doing this will actually allow us to use the substitution rule. To see how this will work let’s simplify the integrand somewhat.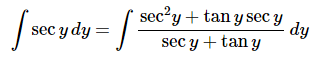
We can now use the following substitution.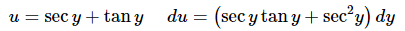
The integral is then,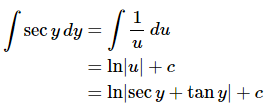
Sometimes multiplying the top and bottom of a fraction by a carefully chosen term will allow us to work a problem. It does however take some thought sometimes to determine just what the term should be.
We can use a similar process for integrating cosecant.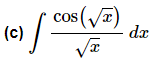
Ans: This next problem has a subtlety to it that can get us in trouble if we aren’t paying attention. Because of the root in the cosine it makes some sense to use the following substitution.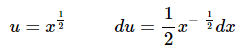
This is where we need to be careful. Upon rewriting the differential we get,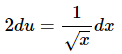
The root that is in the denominator will not become a uu as we might have been tempted to do. Instead it will get taken care of in the differential.
The integral is,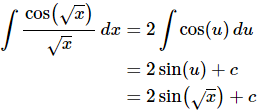
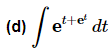
Ans: With this problem we need to very carefully pick our substitution. As the problem is written we might be tempted to use the following substitution,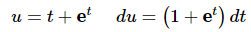
However, this won’t work as you can probably see. The differential doesn’t show up anywhere in the integrand and we just wouldn’t be able to eliminate all the t’s with this substitution.In order to work this problem we will need to rewrite the integrand as follows,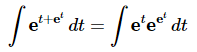
We will now use the substitution,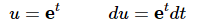
The integral is,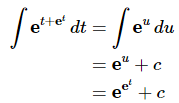
Some substitutions can be really tricky to see and it’s not unusual that you’ll need to do some simplification and/or rewriting to get a substitution to work.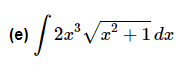
Ans: This last problem in this set is different from all the other substitution problems that we’ve worked to this point. Given the fact that we’ve got more than an x under the root it makes sense that the substitution pretty much has to be,
At first glance it looks like this might not work for the substitution because we have an x3 in front of the root. However, if we first rewrite 2x3=x2(2x) we could then move the 2xto the end of the integral so at least the dudu will show up explicitly in the integral. Doing this gives the following,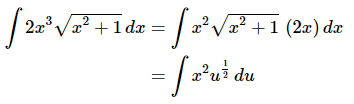
This is a real problem. Our integrals can’t have two variables in them. Normally this would mean that we chose our substitution incorrectly. However, in this case we can rewrite the substitution as follows,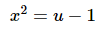
and now, we can eliminate the remaining x’s from our integral. Doing this gives,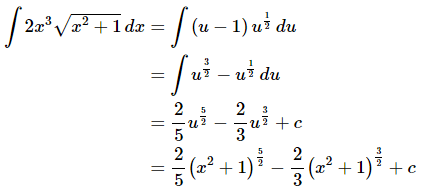
Sometimes, we will need to use a substitution more than once.
This kind of problem doesn’t arise all that often and when it does there will sometimes be alternate methods of doing the integral. However, it will often work out that the easiest method of doing the integral is to do what we just did here.
This final set of examples isn’t too bad once you see the substitutions and that is the point with this set of problems. These all involve substitutions that we’ve not seen prior to this and so we need to see some of these kinds of problems.
Example 5: Evaluate each of the following integrals.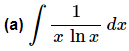
Ans: In this case we know that we can’t integrate a logarithm by itself and so it makes some sense (hopefully) that the logarithm will need to be in the substitution. Here is the substitution for this problem.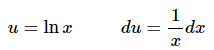
So, the x in the denominator of the integrand will get substituted away with the differential. Here is the integral for this problem.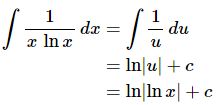
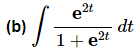
Ans: Again, the substitution here may seem a little tricky. In this case the substitution is,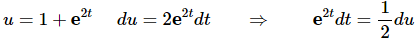
The integral is then,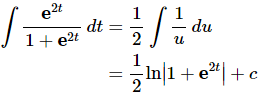
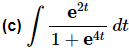
Ans: In this case we can’t use the same type of substitution that we used in the previous problem. In order to use the substitution in the previous example the exponential in the numerator and the denominator need to be the same and in this case they aren’t.
To see the correct substitution for this problem note that,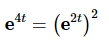
Using this, the integral can be written as follows,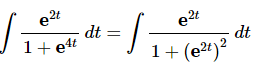
The integral is then,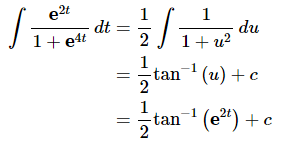
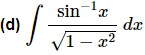
Ans: This integral is similar to the first problem in this set. Since we don’t know how to integrate inverse sine functions it seems likely that this will be our substitution. If we use this as our substitution we get,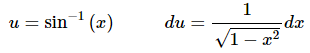
So, the root in the integral will get taken care of in the substitution process and this will eliminate all the xs from the integral. Therefore, this was the correct substitution.The integral is,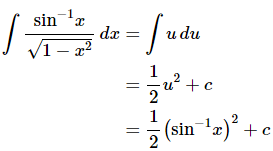
Over the last couple of sections we’ve seen a lot of substitution rule examples. There are a couple of general rules that we will need to remember when doing these problems. First, when doing a substitution remember that when the substitution is done all the x’s in the integral (or whatever variable is being used for that particular integral) should all be substituted away. This includes the x in the dx. After the substitution only u’s should be left in the integral. Also, sometimes the correct substitution is a little tricky to find and more often than not there will need to be some manipulation of the differential or integrand in order to actually do the substitution.
Also, many integrals will require us to break them up so we can do multiple substitutions so be on the lookout for those kinds of integrals/substitutions.
Practice problems: More Substitution Rule
Evaluate each of the following integrals.
Q.1. Evaluate 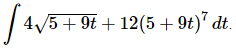
Ans: Don’t get too excited about the fact that there are two terms in this integrand. Each term requires the same substitution,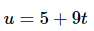
so we’ll simply use that in both terms.
If you aren’t comfortable with the basic substitution mechanics you should work some problems in the previous section as we’ll not be putting in as much detail with regards to the basics in this section. The problems in this section are intended for those that are fairly comfortable with the basic mechanics of substitutions and will involve some more “advanced” substitutions.
Here is the differential work for the substitution.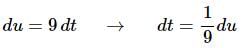
Doing the substitution and evaluating the integral gives,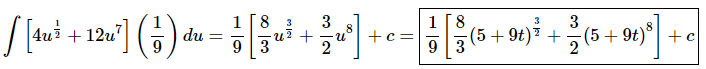
Be careful when dealing with the dt substitution here. Make sure that the 1/9 gets multiplied times the whole integrand and not just one of the terms. You can do this either by using parenthesis (as we’ve done here) or pulling the 1/9 completely out of the integral.
Do not forget to go back to the original variable after evaluating the integral!
Q.2. Evaluate 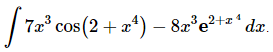
Ans: Don’t get too excited about the fact that there are two terms in this integrand. Each term requires the same substitution,
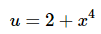
so we’ll simply use that in both terms.
If you aren’t comfortable with the basic substitution mechanics you should work some problems in the previous section as we’ll not be putting in as much detail with regards to the basics in this section. The problems in this section are intended for those that are fairly comfortable with the basic mechanics of substitutions and will involve some more “advanced” substitutions.
Here is the differential work for the substitution.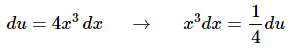
Before doing the actual substitution it might be convenient to factor an x3 out of the integrand as follows.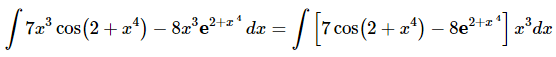
Doing this should make the differential part (i.e. the du part) of the substitution clearer.Now, doing the substitution and evaluating the integral gives,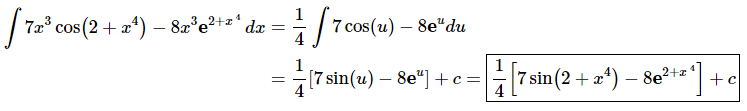 Be careful when dealing with the dx substitution here. Make sure that the 1/4 gets multiplied times the whole integrand and not just one of the terms. You can do this either by using parenthesis around the whole integrand or pulling the 1/4 completely out of the integral (as we’ve done here).
Be careful when dealing with the dx substitution here. Make sure that the 1/4 gets multiplied times the whole integrand and not just one of the terms. You can do this either by using parenthesis around the whole integrand or pulling the 1/4 completely out of the integral (as we’ve done here).
Do not forget to go back to the original variable after evaluating the integral!
Q.3. Evaluate 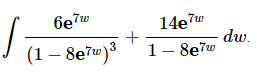
Ans: Don’t get too excited about the fact that there are two terms in this integrand. Each term requires the same substitution,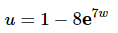
so we’ll simply use that in both terms.
If you aren’t comfortable with the basic substitution mechanics you should work some problems in the previous section as we’ll not be putting in as much detail with regards to the basics in this section. The problems in this section are intended for those that are fairly comfortable with the basic mechanics of substitutions and will involve some more “advanced” substitutions.
Here is the differential work for the substitution.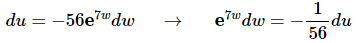
Before doing the actual substitution it might be convenient to factor an e7ω out of the integrand as follows.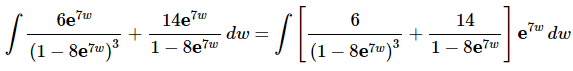
Doing this should make the differential part (i.e. the du part) of the substitution clearer.
Now, doing the substitution and evaluating the integral gives,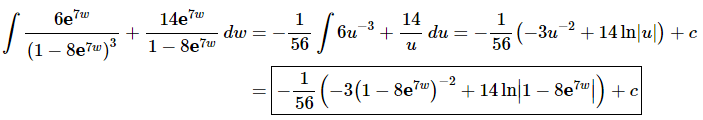
Be careful when dealing with the dw substitution here. Make sure that the -1/56 gets multiplied times the whole integrand and not just one of the terms. You can do this either by using parenthesis around the whole integrand or pulling the - 1/56 completely out of the integral (as we’ve done here).
Do not forget to go back to the original variable after evaluating the integral!
Q.4. Evaluate 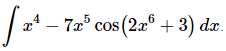
Ans: Clearly the first term does not need a substitution while the second term does need a substitution. So, we’ll first need to split up the integral as follows.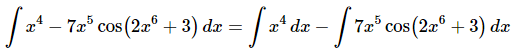
The substitution needed for the second integral is then,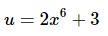
If you aren’t comfortable with the basic substitution mechanics you should work some problems in the previous section as we’ll not be putting in as much detail with regards to the basics in this section. The problems in this section are intended for those that are fairly comfortable with the basic mechanics of substitutions and will involve some more “advanced” substitutions.
Here is the differential work for the substitution.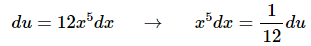
Now, doing the substitution and evaluating the integrals gives,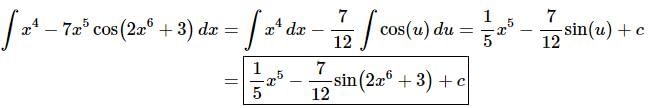
Do not forget to go back to the original variable after evaluating the integral!
Q.5. Evaluate 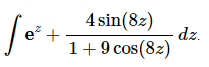
Ans: Clearly the first term does not need a substitution while the second term does need a substitution. So, we’ll first need to split up the integral as follows.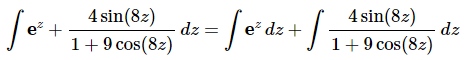
The substitution needed for the second integral is then,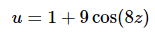
If you aren’t comfortable with the basic substitution mechanics you should work some problems in the previous section as we’ll not be putting in as much detail with regards to the basics in this section. The problems in this section are intended for those that are fairly comfortable with the basic mechanics of substitutions and will involve some more “advanced” substitutions.
Here is the differential work for the substitution.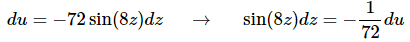
Now, doing the substitution and evaluating the integrals gives,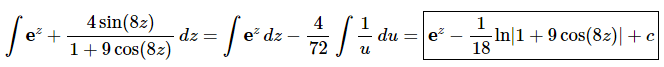
Do not forget to go back to the original variable after evaluating the integral!
Q.6. Evaluate 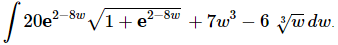
Ans: Clearly the first term needs a substitution while the second and third terms don’t. So, we’ll first need to split up the integral as follows.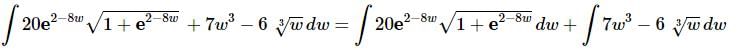
The substitution needed for the first integral is then,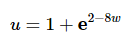
If you aren’t comfortable with the basic substitution mechanics you should work some problems in the previous section as we’ll not be putting in as much detail with regards to the basics in this section. The problems in this section are intended for those that are fairly comfortable with the basic mechanics of substitutions and will involve some more “advanced” substitutions.
Here is the differential work for the substitution.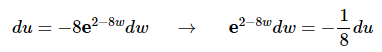
Now, doing the substitutions and evaluating the integrals gives,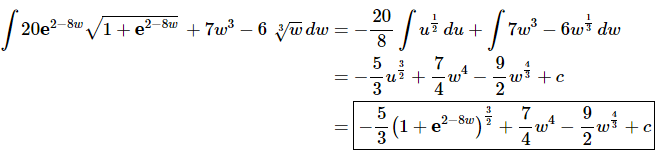
Do not forget to go back to the original variable after evaluating the integral!
Q.7. Evaluate 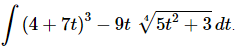
Ans: Clearly each term needs a separate substitution. So, we’ll first need to split up the integral as follows.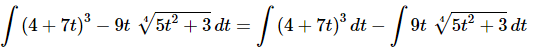
The substitutions needed for each integral are then,
If you aren’t comfortable with the basic substitution mechanics you should work some problems in the previous section as we’ll not be putting in as much detail with regards to the basics in this section. The problems in this section are intended for those that are fairly comfortable with the basic mechanics of substitutions and will involve some more “advanced” substitutions.
Here is the differential work for each substitution.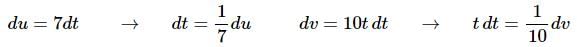
Now, doing the substitutions and evaluating the integrals gives,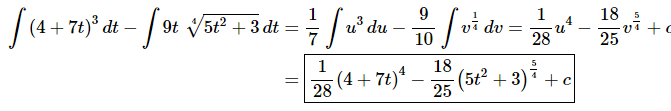
Do not forget to go back to the original variable after evaluating the integral!
Q.8. Evaluate 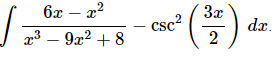
Ans: Clearly each term needs a separate substitution. So, we’ll first need to split up the integral as follows.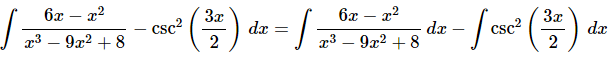
The substitutions needed for each integral are then,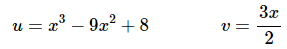
If you aren’t comfortable with the basic substitution mechanics you should work some problems in the previous section as we’ll not be putting in as much detail with regards to the basics in this section. The problems in this section are intended for those that are fairly comfortable with the basic mechanics of substitutions and will involve some more “advanced” substitutions.
Here is the differential work for each substitution.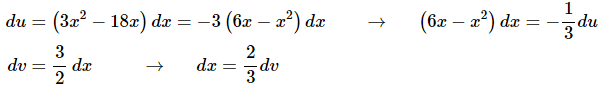
Now, doing the substitutions and evaluating the integrals gives,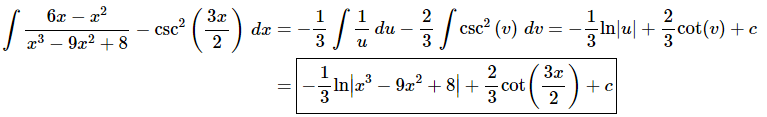
Do not forget to go back to the original variable after evaluating the integral!
Q.9. Evaluate 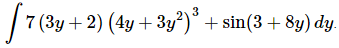
Ans: Clearly each term needs a separate substitution. So, we’ll first need to split up the integral as follows.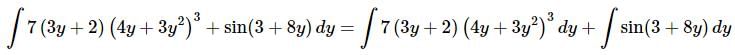
The substitutions needed for each integral are then,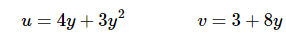
If you aren’t comfortable with the basic substitution mechanics you should work some problems in the previous section as we’ll not be putting in as much detail with regards to the basics in this section. The problems in this section are intended for those that are fairly comfortable with the basic mechanics of substitutions and will involve some more “advanced” substitutions.
Here is the differential work for each substitution.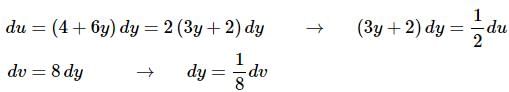
Now, doing the substitutions and evaluating the integrals gives,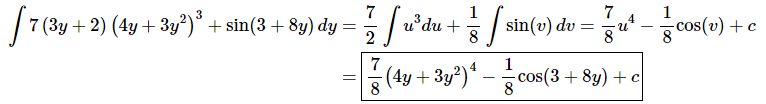
Do not forget to go back to the original variable after evaluating the integral!
Q.10. Evaluate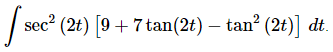
Ans: This integral can be a little daunting at first glance. To do it all we need to notice is that the derivative of tan (x) is sec2 (x) and we can notice that there is a sec2 (2t) times the remaining portion of the integrand and that portion only contains constants and tangents.
So, it looks like the substitution is then,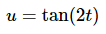
If you aren’t comfortable with the basic substitution mechanics you should work some problems in the previous section as we’ll not be putting in as much detail with regards to the basics in this section. The problems in this section are intended for those that are fairly comfortable with the basic mechanics of substitutions and will involve some more “advanced” substitutions.
Here is the differential work for the substitution.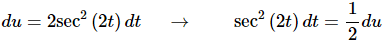
Now, doing the substitution and evaluating the integrals gives,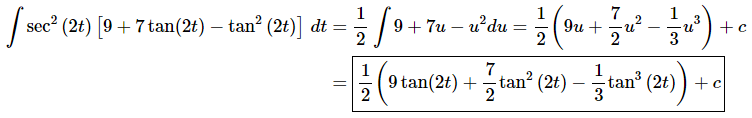
Do not forget to go back to the original variable after evaluating the integral!
Q.11. Evaluate 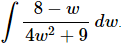
Ans: As written we can’t do this problem. In order to do this integral we’ll need to rewrite the integral as follows.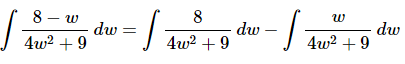
Now, the first integral looks like it might be an inverse tangent (although we’ll need to do a rewrite of that integral) and the second looks like it’s a logarithm (with a quick substitution).
So, here is the rewrite on the first integral.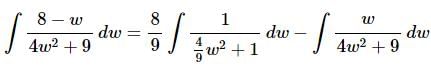
Now we’ll need a substitution for each integral. Here are the substitutions we’ll need for each integral.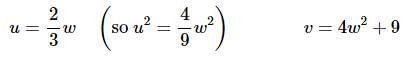
Here is the differential work for the substitution.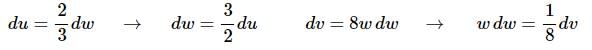
Now, doing the substitutions and evaluating the integrals gives,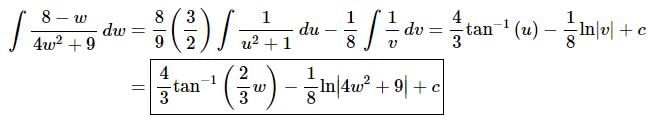
Do not forget to go back to the original variable after evaluating the integral!
Q.12. Evaluate 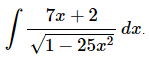
Ans: As written we can’t do this problem. In order to do this integral we’ll need to rewrite the integral as follows.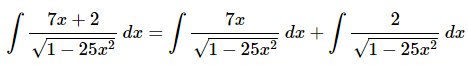
Now, the second integral looks like it might be an inverse sine (although we’ll need to do a rewrite of that integral) and the first looks like a simple substitution will work for us.
So, here is the rewrite on the second integral.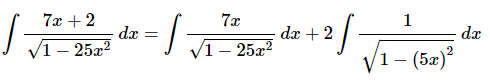
Now we’ll need a substitution for each integral. Here are the substitutions we’ll need for each integral.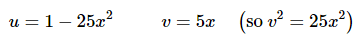
Here is the differential work for the substitution.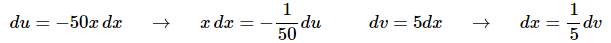
Now, doing the substitutions and evaluating the integrals gives,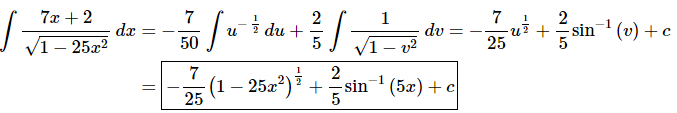
Do not forget to go back to the original variable after evaluating the integral!
Q.13. Evaluate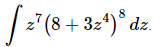
Ans: Okay, the “obvious” substitution here is probably,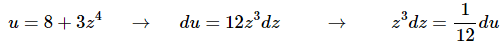
however, that doesn’t look like it might work because of the z7.
Let’s do a quick rewrite of the integrand.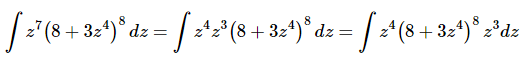
Now, notice that we can convert all of the z’s in the integrand except apparently for the z4 that is in the front. However, notice from the substitution that we can solve for z4 to get,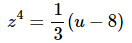
With this we can now do the substitution and evaluate the integral.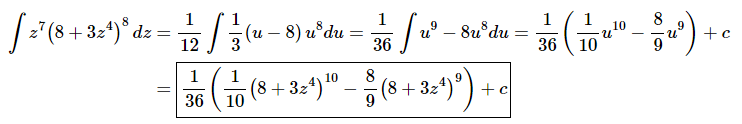
|
112 videos|65 docs|3 tests
|
FAQs on More Substitution Rule - Calculus - Mathematics
| 1. What is the substitution rule in mathematics? |  |
| 2. How does the substitution rule work in calculus? |  |
| 3. When should I use the substitution rule in mathematics? |  |
| 4. Can you provide an example of applying the substitution rule in mathematics? |  |
| 5. Are there any limitations or conditions to be aware of when using the substitution rule? |  |





















