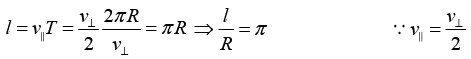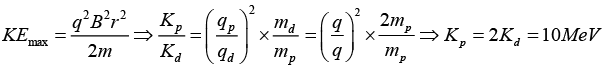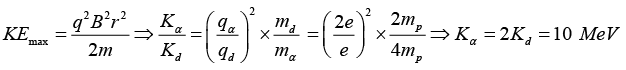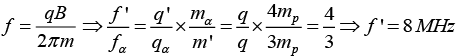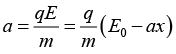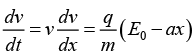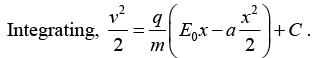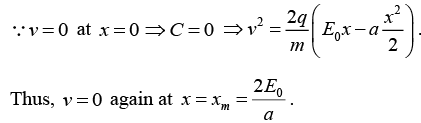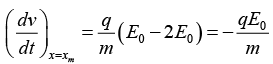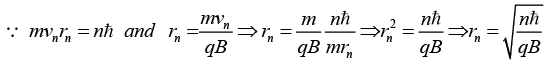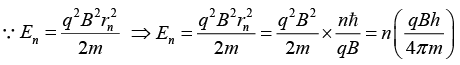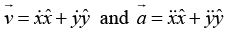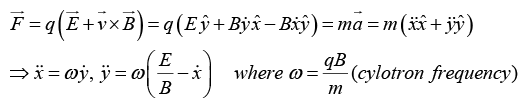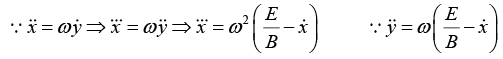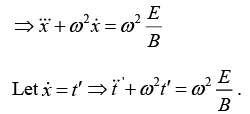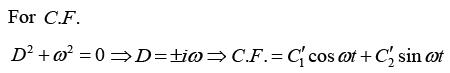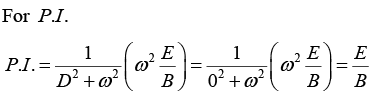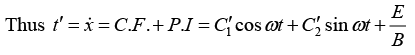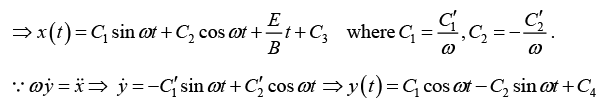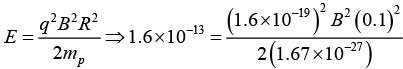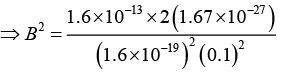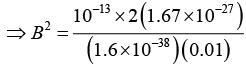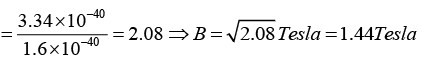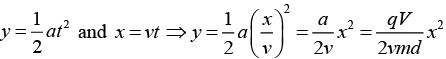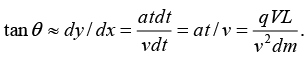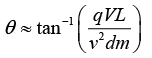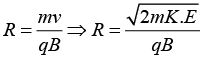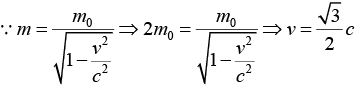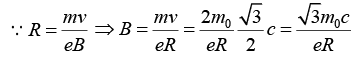Motion of Charged Particle in Uniform Electric & Magnetic Field: Assignment | Electricity & Magnetism - Physics PDF Download
Q.1. A charged particle moves in a helical path under the influence of a constant magnetic field. The initial velocity is such that the component along the magnetic field is half the component in the plane normal to the magnetic field. Find the ratio ℓ/R of the pitch ℓ to the radius R of the helical path.
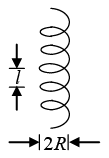
Pitch of the helix
Q.2. The maximum energy of deuteron coming out of a cyclotron accelerator is 5 MeV.
(a) What is the maximum energy of protons that can be obtained from the accelerator?
(b) What is the maximum energy of a -particle that can be obtained from the accelerator?
(c) In a cyclotron, α-particles are accelerated using RF source of frequency 6 MeV.
What would be the frequency of RF source if α-particles are replaced by 2He3 particles?
(a)
(b)
(c)
Q.3. A particle with charge q and mass m moves linearly due to an electric field E = E0- ax, where a is a positive constant, x is the distance from the point where the particle was initially at rest.
(a) Find the distance covered by the particle till the moment it came to rest.
(b) Find the acceleration of the particle till the moment it came to rest.
(a) Acceleration of the particle is
The equation of motion is,
(b) The corresponding acceleration is,
Q.4. A particle of mass m carrying charge q is moving in a circle in a magnetic field B. According to Bohr’s model, find
(a) the radius of the particle in the nth level.
(b) the energy of the particle in the nth level.
(a)
(b)
Q.5. Consider points in z -direction and
points in z -direction and 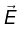 points in y -direction, and a particle of mass m and charge q at rest is released from origin.
points in y -direction, and a particle of mass m and charge q at rest is released from origin.
(a) In which plane charge particle will confine.
(b) Write the coupled differential equation whose solution represents the path of the charged particle.
(c) Find the solution of coupled differential equation.
(d) Write the equation of cycloid.
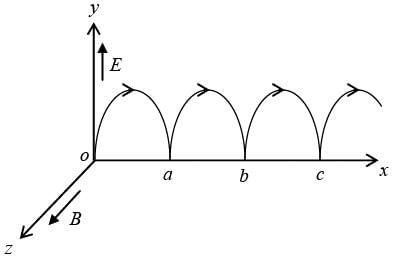
If
points in z -direction and
points in y -direction, and a particle at rest is released from origin, then particle will follow cycloid motion. Initially, the particle is at rest, so the magnetic force is zero, and the electric field accelerates the charge in y-direction. As it speeds up, a magnetic force develops which pulls the charge to the right. The faster it goes stronger the magnetic force becomes and it curves the particle back around towards the x-axis. At this point the charge is moving against the electric force, so it begins to slow down-the magnetic force then decreases, and the electrical force takes over, bringing the charge to rest at point a and then process repeats.
(a) Charge particle will confine in a plane that is perpendicular to. So it will confine in
xy -plane.
(b)
(c) Let us solve the above differential equations,
This is the formula for a circle, of radius R , whose center is ( Rwt, R, 0 ) travels in the x -direction at constant speed,
The curve generated in this way is called a cycloid.
Q.6. Find the value of the magnetic field required to maintain non-relativistic protons of energy 1MeV in a circular orbit of radius 100mm. (Given: mp = 1.67x10-27 kg, e= 1.6x10-19 C)
Q.7. The figure below shows the trajectory of a particle that is deflected as it moves through the uniform electric field between parallel plates. There is potential difference V and distance d between the plates, and they have length L. The particle (mass m, charge q) has nonrelativistic speed v before it enters the field, and its direction at this time is perpendicular to the field. For small deflections, which of the following expressions is the best approximation to the deflection angle θ ?
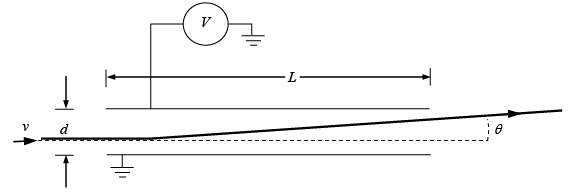
(a) Find the acceleration of the charged particle.
(b) Find the path of the charged particle
(c) Find angle of deflection when charged particle leaves the field region.
(a) Assuming that there is no magnetic field, one has from the Lorentz force F = ma = qE = qV / d , where one neglects gravitational acceleration.
The acceleration is constant, and it is a = qV /(dm).
(b)
Thus path is parabolic.
(c) y = 0.5 at2 ⇒ dy = atdt and the fact that x = L = vt ⇒ dx = vdt and t = L / v, one can calculate the angle as
Q.8. A proton, deuteron and an α-particle having the kinetic energy K.Ep=2K, K.Ed =4K and K.Eα = 8K are moving in circular trajectories in a constant magnetic field. If Rp, Rd and Rα denote respectively the radii of the trajectories of these particles, then find the ratio Rp : Rd : Rα.
⇒ Rp: Rd: Rα = 2:4:4 = 1:2:2
Q.9. A particle with charge q and momentum p is moving in the horizontal plane under the action of a uniform vertical magnetic field of magnitude B. Measurements are made of the particle’s trajectory to determine the “sagitta” s and half-chord length ℓ, as shown in the figure. Show that the particle’s momentum is qBℓ2/2s ? (Assume s << ℓ . )
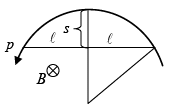
Equating the centripetal force with the Lorentz Force, mv2 /R = qvB.
The radius of curvature used in the centripetal force equation is given by R2 = l2+ (R-s)2,
⇒ R2 = l2 + (R-s)2 = l2 + R2+s2 - 2RS ≈ l2 + R2 - 2Rs + O(s2) ∵ s<<l
⇒ l2 = 2Rs ⇒ R = l2/(2s)
Now mv/R = qB ⇒ 2smv/l2 = qB ⇒ p = mv = qBl2/2s,
Q.10. The maximum relativistic kinetic energy of β-particles from a radioactive nucleus is equal to the rest mass energy of the particle. A magnetic field is applied perpendicular to the beam of β-particles, which bends it to a circle of radius R . Show that magnetic field needed is given by 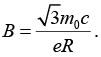 (where m0 is rest mass energy)
(where m0 is rest mass energy)
KEmax = mc2 - m0c2 = m0c2 ⇒ m = 2m0
|
82 videos|32 docs|22 tests
|
FAQs on Motion of Charged Particle in Uniform Electric & Magnetic Field: Assignment - Electricity & Magnetism - Physics
| 1. What is the motion of a charged particle in a uniform electric field? |  |
| 2. How does a magnetic field affect the motion of a charged particle? |  |
| 3. How are electric and magnetic fields combined to affect the motion of a charged particle? |  |
| 4. What is the role of velocity in the motion of a charged particle in electric and magnetic fields? |  |
| 5. How can the motion of a charged particle in uniform electric and magnetic fields be described quantitatively? |  |