Multivariable Integral | Engineering Mathematics - Engineering Mathematics PDF Download
Introduction
- Principal application of vector function is the analysis of motion is space. The gradient defines the normal to the tangent plane, the directional derivatives give the rate of change in any given direction.
- If is the velocity field of a fluid flow, then divergence of E at appoint P (x, y, z) (Flux density) is the rate at which fluid is (diverging) piped in or drained away at P, and the curl (or circular density) is the vector of greatest circulation in flow, we express grad, div and curl in general curvilinear.
- Coordinate and in cylindrical and spherical. Coordinates which are useful in engineering physics or geometry involving a cylinder or cone or a sphere.
Scalar Function: Scalar function of scalar variable t is a function F = f(t) which uniquely associated a scaIar F(t) for every value of the scalar t In an internal [a, b]
Scalar Field: Scalar field Is a region in space such that for every point P In this region the scalar function F associates a scalar F(P).
Vector Function: Vector function of a scalar variable t is a function F̅ = F̅(t) which uniquely associates a vector F̅ for each scalar t.
Vector Field: Vector Field is a region in space such that with every point in that region. Vector function V̅ associates a vector V̅ (P)
Derivatives of a vector function
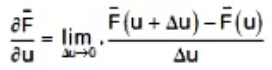
u → Scalar Variable
Derivative in the Component form
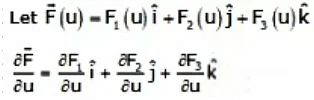
Gradient of a scalar function
Gradient F denoted by 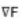 and defined as
and defined as
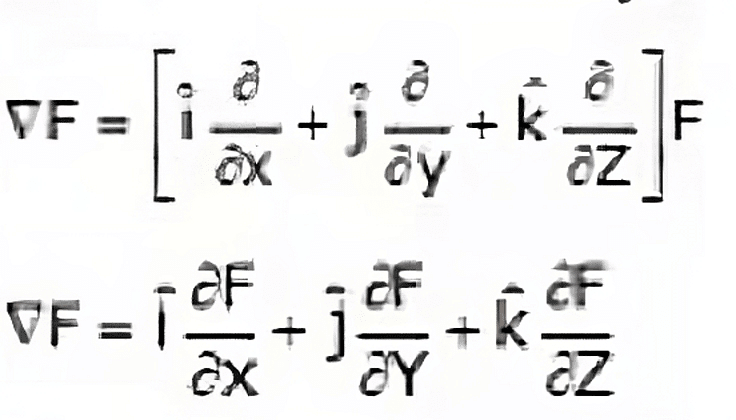
Gradient is defined only for scalar function and the gradient of any scalar function will be a vector
Divergence
Divergence of a vector function A̅(x,y,z) is written as divergence of A̅ and denoted by ▽. A̅ id defind as
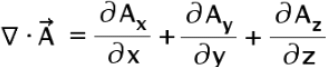 = a scalar quantity
= a scalar quantity
Solenoidal: A̅ is said to be solenoid if ▽. A̅ = 0 (at all point of function)
Curl
Curl of A̅ denoted by ▽x A̅ also known as rotaion ▽ of rotation of ▽ is defind as curl of A̅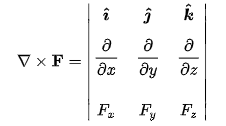
which comes out to be a vector quantity.
Irrotational Field: A vector point function A̅ is aid to be irrotational, if curl of A̅ is zero at every point
▽x A̅ = 0
Vector integral calculus
Vector integral calculus extends the concept of (ordinary) integral calculus to vector functions It has application in fluid flow, design of underwater transmission cables, heat flow in stars, study of satellite.
1. Line Integral: Line integral are useful in the calculation of work done by variable forces along path in space and the rates at which fluids flow along curves (circulation) and across boundaries. Let C be curve defined from A to B with corresponding arc length S = a and S = b respectively. Divide C into arbitrary portions.

2. Surface integral: The concept of surface integral is a simple and generalization of a double integral
∫∫R F(x,y)dx.dy
Taken over a plane region R. In a surface integral F (x, y) in integrated, over a curved surface.
3. Volume Integral: Let V be a region in space enclosed by a closed surface  be a vector point function. Then the triple integral.
be a vector point function. Then the triple integral.
Green’s Theorem
If R is a closed region in the x-y plane bounded by a single closed curve C and if M (x, y) and N (x, y) are continuous function of x and y having continuous derivative in R then
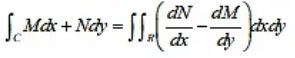
Stroke Theorem
Transformation between line integral and surface integral. Let A' be a vector having continuous first partial derivative in a domain in space containing an open two sided surface S bounded a simple closed curve C then

where n' is a unit normal of A and C is traversed in the positive direction.
Green's Theorem in plane is a special case of stroke theorem.
Gauss Divergence Theorem
Transformation between surface integral and volume integral. Let A' be a vector function of position having continuous derivatives. In a volume V bounded by a closed surfaces S them

Where n' is the downward (position) normal to S.
|
65 videos|129 docs|94 tests
|
















