Multiplexing & Digital Coding Techniques | Communication System - Electronics and Communication Engineering (ECE) PDF Download
Multiplexing
- Multiplexing is a technique in which several message signals are combined into a composite signal for transmission over a common channel. In order to transmit a number of these signals over the same channel, the signal must be kept apart so that they do not interfere with each other, and hence they can be separated easily at the receiver end.
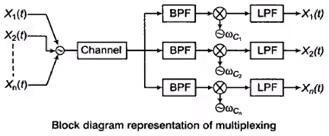
- Digital radio has developed ways in which more than one conversation can be accommodated (multiplexed) inside the same physical RF channel. There are three common ways of achieving this:
- Frequency Division Multiple Access (FDMA)
- Time Division Multiple Access (TDMA)
- Code Divisional Multiple Access (CDMA)
Frequency Division Multiplexing
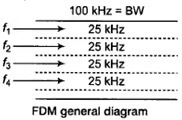
- In FDMA, we divide whole bandwidth of the channel in small segments and allot it to different users so that they can access channel at the same time by using their allotted bandwidth.
Time Division Multiplexing
- In TDMA, whole time slot is divided among different users so that at a time only one user is accessing the channel.

Key Points:
- Bandwidth requirement in TDMA and FDMA is almost same for the same number of users.
- The TDMA system can be used to multiplex analog or digital signals, however, it is more suitable for the digital signal multiplexing.
- The communication channel over which the TDMA signal is travelling should ideally have an infinite bandwidth in order to avoid the signal distortion. Such channels are known as the band-limited channels.
Code Division Multiplexing (CDMA)
- Instead of splitting the RF channel in to sub-channels or time slots, each slot has a unique code. Unlike FDMA, the transmitted RF frequency is the same in each slot, and unlike TDMA, the slots are transmitted simultaneously. In the diagram, the channel is split in to four code slots. Each slot is still capable of carrying a separate conversation because the receiver only reconstructs information sent from a transmitter with the same code.
Introduction to Coding Technique:
Codes can either correct or merely detect errors depends the redundancy contained in the code. Codes that can detect errors are called error-detecting codes, and codes that can correct errors are known as error-correcting codes. There are many different error control codes. These are divided into two types of codes i.e., block codes and convolutional codes. These two codes are described by binary codes which consist of only two elements i.e., 0.1. The set {0, 1} is denoted K.
Channel Coding:
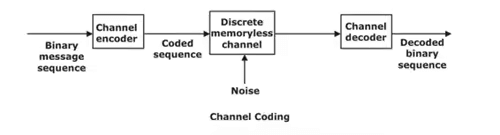
A basic block diagram for the channel coding is shown in Figure below. The binary data sequence at the input terminal of the channel encoder may be the output of a source encoder.By adding extra bits into the message bits by the channel encoder for detection and correction of the bit errors in the oringinal input data is done at the receiver.The added extra bits leads to symmetric redundancy. The channel decode at the receiver side remove this symmetric reduncdancy by providing the actual transmitted data. The main objective of channel encoder and decoder is to reduce the channel noise effect.
Linear Block Codes :
Binary Field :
The binary field has two operations, addition and multiplication such that the results of all operations are in K.The set K = {0, 1) is a binary field. The rules of addition and multiplication are as follows:
Addition:
0 ⊕ 0 = 0 1 ⊕ 1 = 0 0 ⊕ 1 = 1 ⊕ 0 = 1
Multiplication:
0 ⋅ 0 = 0 1 ⋅ 1 = 1 0 ⋅ 1 = 1 ⋅ 0 = 0
Linear Codes:
Let a = (a1, a2, ... ,an), and b = (b1, b2, . . . ,bn) be two code words in a code C. The sum of a and b, denoted by a ⊕ b, is defined by (a1 ⊕ b1, a2 ⊕ b2, . . . , an ⊕ bn). A code C is called linear if the sum of two code words is also a code word in C. A linear code C must contain the zero code word o = (0, 0,.. . ,0), since a ⊕ a = 0.
Hamming Weight and Distance :
Let C be a code word with length n. The Hamming weight of C denoted by w(c), is the number of 1’s in C.
Let a and b be code words of length n. The hamming distance between a and b is represented by d (a,b) means the number of position where a , b are differ. Thus, the Hamming weight of a code word c is the Hamming distance between c and 0, that is
w(c) = d(c, 0)
Similarly, the Hamming distance can be written in terms of Hamming weight as
d(a, b) = w(a ⊕ b)
Minimum Distance:
The minimum distance dmin of a linear code C is defined as the smallest Hamming distance between any pair of code words in C.
From the closure property of linear codes–that is, the sum (module 2) of two code words is also a code word.
Theorem 1 :
“The minimum distance dmin of a linear code C is defined as the smallest Hamming weight of the non-zero code word in the linear code C.”
Error Detection and Correction Capabilities:
The minimum distance dmin of a linear code C is an important parameter of C. It determines the error detection and correction capabilities of C. This is stated in the following theorems.
Theorem 2:
“In a linear code (C ) of minimum distance dmin is useful to detect up to t errors by following the condition.
dmin ≥ t + 1”
Theorem 3:
“A linear code C of minimum distance dmin can correct up to t errors if and only if
dmin ≥ 2t + 1 "
, there exists a received word r such that d(ci, r) ≤ t, and yet r is as close to cj as it is to ci. Thus, the decoder may choose cj, which is incorrect.
Generator Matrix :
In a (n, k) linear block code C, we define a code vector c and a data (or message) vector d as follows:
c = [c1,c2,...,cn]
d = [d1,d2,...,dk]
If the data bits appear in specified location of C, then the code C is named systematic code. Otherwise, it is called non-systematic. Here we assume that the first k bits of c are the data bits and the last (n–k) bits are the parity-check bits formed by linear combination of data bits, that is,
ck+1 = p11d1 ⊕ p12d2 ⊕ ⋅ ⋅ ⋅ ⊕ p1kdk
ck+2 = p21d1 ⊕ p22d2 ⊕ ⋅ ⋅ ⋅ ⊕ p2kdk
⋮
ck+m = pm1d1 ⊕ pm2d2 ⊕ ⋅ ⋅ ⋅ ⊕ pmkdk
where m = n – k. Above equation can be written in a matrix form as:

where G = [Ik PT]
where Ik is the kth-order identity matrix and PT is the transpose of the matrix P given by
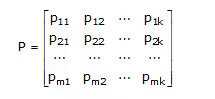
The k X n matrix G is called the Generator Matrix. Note that a generator matrix for C must have k rows and n columns, and it must have rank k; that is, the k rows of G are linearly independent.
Parity-Check Matrix:
Let H denote an m X n matrix defined by
H = [P Im]
where m = n – k and Im is the mth-order identity matrix. Then
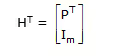
Using above equations, we have
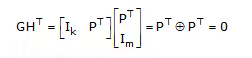
where 0 denotes the k × m zero matrix. Now we have,
cHT = dGHT = 0
where 0 denotes the 1 × m zero vector.
The matrix H is called the parity-check matrix of C. Note that the rank of H is m = n – k and the rows of H are linearly independent. The minimum distance dmin of a linear block code C is closely related to the structure of the parity-check matrix H of C.
Syndrome Decoding:
Let r denote the received word of length n when code word c of length n was sent over a noisy channel. Then, r = c ⊕ e, where 'e' is termed as the error pattern.
Note that e = r + c.
let us consider first, the case of a single error in the ith position. Then we can represent e by e = [0 . . . 010 . . . 0]
Next, we evaluate rHT and obtain
rHT = (c ⊕ e)HT = cHT ⊕eHT = eHT = S
Here, S is called the syndrome of r.
Thus, using s and noting that eHT is the ith row of HT. Now we can find the error position by comparing S to the of HT . Decoding by this simple comparison method is called syndrome decoding. Note that by using syndrome decoding technique all error patterns can correctly decoded. The zero syndrome indicates that r is a code word and is presumably correct.
With syndrome decoding, an (n, k) linear block code can correct up to t errors per codeword if n and k satisfy the following Hamming bound.
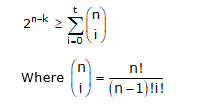
NOTE: The Hamming bound is necessary but not sufficient for the construction of a t-error correcting linear block code.
|
14 videos|38 docs|30 tests
|
FAQs on Multiplexing & Digital Coding Techniques - Communication System - Electronics and Communication Engineering (ECE)
| 1. What is multiplexing? |  |
| 2. What is frequency division multiplexing (FDM)? |  |
| 3. How does time division multiplexing (TDM) work? |  |
| 4. What is code division multiplexing (CDMA)? |  |
| 5. What are linear block codes and their properties? |  |

|
Explore Courses for Electronics and Communication Engineering (ECE) exam
|

|

















