Multiplication Algorithm & Division Algorithm - Computer Science Engineering (CSE) PDF Download
Multiplication Algorithm & Division Algorithm
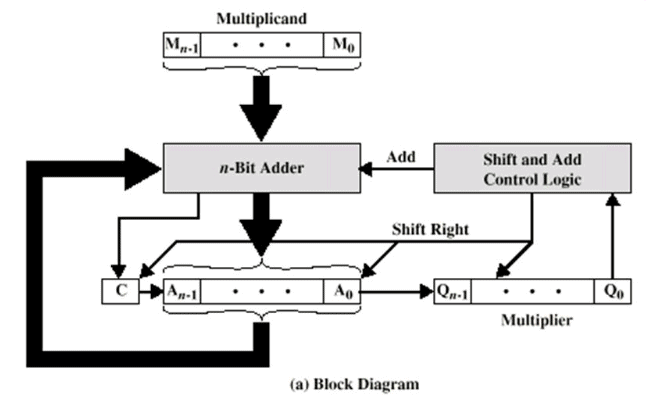
The multiplier and multiplicand bits are loaded into two registers Q and M. A third register A is initially set to zero. C is the 1-bit register which holds the carry bit resulting from addition. Now, the control logic reads the bits of the multiplier one at a time. If Q0 is 1, the multiplicand is added to the register A and is stored back in register A with C bit used for carry. Then all the bits of CAQ are shifted to the right 1 bit so that C bit goes to An-1, A0 goes to Qn-1 and Q0 is lost. If Q0 is 0, no addition is performed just do the shift. The process is repeated for each bit of the original multiplier. The resulting 2n bit product is contained in the QA register.
There are three types of operation for multiplication.
- It should be determined whether a multiplier bit is 1 or 0 so that it can designate the partial product. If the multiplier bit is 0, the partial product is zero; if the multiplier bit is 1, the multiplicand is partial product.
- It should shift partial product.
- It should add partial product.




Algorithm:
Step 1: Clear the sum (accumulator A). Place the multiplicand in X and multiplier in Y.
Step 2: Test Y0; if it is 1, add content of X to the accumulator A.
Step 3: Logical Shift the content of X left one position and content of Y right one position.
Step 4: Check for completion; if not completed, go to step 2.

Signed Multiplication (Booth Algorithm) – 2’s Complement Multiplication
Multiplier and multiplicand are placed in Q and M register respectively. There is also one bit register placed logically to the right of the least significant bit Q0 of the Q register and designated as Q-1. The result of multiplication will appear in A and Q resister. A and Q-1 are initialized to zero if two bits (Q0 and Q-1) are the same (11 or 00) then all the bits of A, Q and Q-1 registers are shifted to the right 1 bit. If the two bits differ then the multiplicand is added to or subtracted from the A register depending on weather the two bits are 01 or 10. Following the addition or subtraction the arithmetic right shift occurs. When count reaches to zero, result resides into AQ in the form of signed integer [-2n-1*an-1 + 2n-2*an-2 + …………… + 21*a1 + 20*a0].


Division Algorithm
Division is somewhat more than multiplication but is based on the same general principles. The operation involves repetitive shifting and addition or subtraction.
First, the bits of the dividend are examined from left to right, until the set of bits examined represents a number greater than or equal to the divisor; this is referred to as the divisor being able to divide the number. Until this event occurs, 0s are placed in the quotient from left to right. When the event occurs, a 1 is placed in the quotient and the divisor is subtracted from the partial dividend. The result is referred to as a partial remainder. The division follows a cyclic pattern. At each cycle, additional bits from the dividend are appended to the partial remainder until the result is greater than or equal to the divisor. The divisor is subtracted from this number to produce a new partial remainder. The process continues until all the bits of the dividend are exhausted.


Restoring Division (Unsigned Binary Division)
Algorithm:
Step 1: Initialize A, Q and M registers to zero, dividend and divisor respectively and counter to n where n is the number of bits in the dividend.
Step 2: Shift A, Q left one binary position.
Step 3: Subtract M from A placing answer back in A. If sign of A is 1, set Q0 to zero and add M back to A (restore A). If sign of A is 0, set Q0 to 1.
Step 4: Decrease counter; if counter > 0, repeat process from step 2 else stop the process. The final remainder will be in A and quotient will be in Q.

Quotient in Q = 0011 = 3
Remainder in A = 00011 = 3
Non – Restoring Division (Signed Binary Division) Algorithm
Step 1: Initialize A, Q and M registers to zero, dividend and divisor respectively and count to number of bits in dividend.
Step 2: Check sign of A;
If A < 0 i.e. bn-1 is 1
a. Shift A, Q left one binary position.
b. Add content of M to A and store back in A.
If A ≥ 0 i.e. bn-1 is 0
a. Shift A, Q left one binary position.
b. Subtract content of M to A and store back in A.
Step 3: If sign of A is 0, set Q0 to 1 else set Q0 to 0.
Step 4: Decrease counter. If counter > 0, repeat process from step 2 else go to step 5.
Step 5: If A ≥ 0 i.e. positive, content of A is remainder else add content of M to A to get the remainder. The quotient will be in Q.


FAQs on Multiplication Algorithm & Division Algorithm - Computer Science Engineering (CSE)
| 1. What is the Multiplication Algorithm? |  |
| 2. What is the Division Algorithm? |  |
| 3. What are the benefits of using the Multiplication and Division Algorithms? |  |
| 4. How do the Multiplication and Division Algorithms differ from traditional methods of arithmetic? |  |
| 5. Can the Multiplication and Division Algorithms be used for larger numbers? |  |



















