Year 3 Exam > Year 3 Notes > Year 3 Mathematics > Multiply a 2-digit by a 1-digit number
Multiply a 2-digit by a 1-digit number | Year 3 Mathematics PDF Download
Mental method for multiplication
One method involves breaking down numbers mentally. For instance:
Example: Consider the calculation: What is 6 x 40?
Ans: 6 x 40 equals 6 x 4 x 10
Firstly, calculate 6 x 4, which equals 24
Next, multiply 24 by 10. When you multiply by 10, all digits shift one place to the left, adding a zero to represent the increased value:
24 x 10 = 240
Written Methods for Multiplication
- In mathematics, when multiplying a 2-digit number by a 1-digit number, using a written method known as short multiplication can often simplify the process.
- This method, also called short multiplication, aids in organizing the multiplication steps effectively.
Solved Examples
Example 1: Beverley ordered 8 packets of balloons. Each packet contained 52 balloons. How many balloons has she got in total?
Sol: The equation we are working out is:
52 x 8
First, set the multiplication out correctly: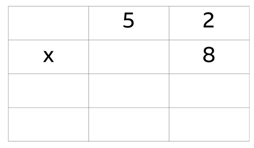
Step 1: Now the multiplication is set out correctly, you can solve the multiplication in the ones column.
2 x 8 = 16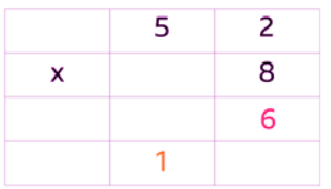
Remember to carry the 1 into the tens column.
Step 2: Now it's time to work out 50 x 8
50 x 8 = 400
Don’t forget about the ten you carried over: 400 + 10 = 410.
52 x 8 = 416
Beverley now has 416 balloons.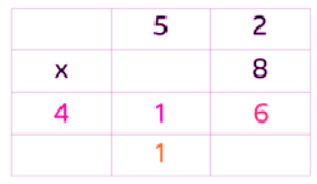
Example 2: What is 48 x 6?
Sol: When you set out short multiplication, it is important to make sure the place value of the digits are in the correct place.
Put the 4 in the tens column and the 8 in the ones column.
Like this:
Step 1: Just like when you solve column addition and subtraction, you start with the digits in the ones.
8 x 6 = 48
Since 48 is 4 tens and 8 ones, you have to remember to keep the place values in the correct column. The 8 stays in the ones column, while you carry the 4 into the tens column.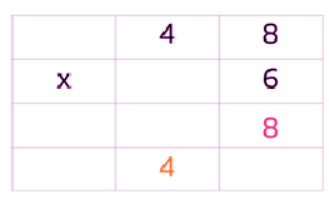
Step 2: Time to work out 40 x 6 now.
40 x 6 = 240
But you can’t forget about the 4 tens that you carried over - you need to remember to add that on to the answer.
240 + 40 = 280
Again, make sure everything is in the correct place value column.
48 x 6 = 288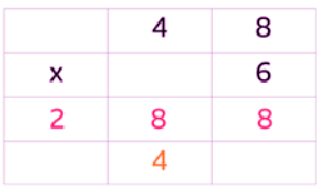
The document Multiply a 2-digit by a 1-digit number | Year 3 Mathematics is a part of the Year 3 Course Year 3 Mathematics.
All you need of Year 3 at this link: Year 3
|
69 videos|67 docs|11 tests
|
FAQs on Multiply a 2-digit by a 1-digit number - Year 3 Mathematics
| 1. What is the process for dividing up to 4 digits by 1 digit? |  |
Ans. To divide a number up to 4 digits by a 1-digit number, you would follow the traditional long division method. Start by dividing the leftmost digits, carry down the next digit, and continue the process until you reach the end of the number.
| 2. How can you multiply a 2-digit number by a 1-digit number? | |
Ans. To multiply a 2-digit number by a 1-digit number, you would use the traditional multiplication method. Multiply the 1-digit number by each digit of the 2-digit number separately, then add the results together to get the final answer.
| 3. Why is it important to understand dividing and multiplying with multiple digits in mathematics? | |
Ans. Understanding dividing and multiplying with multiple digits is important in mathematics as it helps in solving more complex problems, improves problem-solving skills, and lays the foundation for higher-level math concepts.
| 4. What are some common challenges students face when learning to divide and multiply with multiple digits? | |
Ans. Some common challenges students face when learning to divide and multiply with multiple digits include understanding the concept of place value, remembering the steps of long division and multiplication, and making errors in carrying over digits.
| 5. How can students improve their skills in dividing up to 4 digits by 1 digit and multiplying a 2-digit by a 1-digit number? | |
Ans. Students can improve their skills in dividing and multiplying with multiple digits by practicing regularly, seeking help from teachers or tutors when needed, and using online resources and worksheets to reinforce their understanding of the concepts.
Related Exams
About this Document
|
Dec 22, 2024 Last updated |
Document Description: Multiply a 2-digit by a 1-digit number for Year 3 2024 is part of Year 3 Mathematics preparation.
The notes and questions for Multiply a 2-digit by a 1-digit number have been prepared according to the Year 3 exam syllabus. Information about Multiply a 2-digit by a 1-digit number covers topics
like Mental method for multiplication, Solved Examples and Multiply a 2-digit by a 1-digit number Example, for Year 3 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Multiply a 2-digit by a 1-digit number.
Introduction of Multiply a 2-digit by a 1-digit number in English is available as part of our Year 3 Mathematics
for Year 3 & Multiply a 2-digit by a 1-digit number in Hindi for Year 3 Mathematics course.
Download more important topics related with notes, lectures and mock test series for Year 3
Exam by signing up for free. Year 3: Multiply a 2-digit by a 1-digit number | Year 3 Mathematics
Description
Full syllabus notes, lecture & questions for Multiply a 2-digit by a 1-digit number | Year 3 Mathematics - Year 3 | Plus excerises question with solution to help you revise complete syllabus for Year 3 Mathematics | Best notes, free PDF download
Information about Multiply a 2-digit by a 1-digit number
In this doc you can find the meaning of Multiply a 2-digit by a 1-digit number defined & explained in the simplest way possible. Besides explaining types of
Multiply a 2-digit by a 1-digit number theory, EduRev gives you an ample number of questions to practice Multiply a 2-digit by a 1-digit number tests, examples and also practice Year 3
tests
|
Explore Courses for Year 3 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Multiply a 2-digit by a 1-digit number | Year 3 Mathematics
,past year papers
,mock tests for examination
,Exam
,MCQs
,Multiply a 2-digit by a 1-digit number | Year 3 Mathematics
,Viva Questions
,Sample Paper
,Semester Notes
,video lectures
,study material
,Summary
,practice quizzes
,Extra Questions
,Important questions
,Multiply a 2-digit by a 1-digit number | Year 3 Mathematics
,Free
,Previous Year Questions with Solutions
,Objective type Questions
,ppt
,shortcuts and tricks
;
Additional Information about Multiply a 2-digit by a 1-digit number for Year 3 Preparation
Multiply a 2-digit by a 1-digit number Free PDF Download
The Multiply a 2-digit by a 1-digit number is an invaluable resource that delves deep into the core of the Year 3 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Multiply a 2-digit by a 1-digit number now and kickstart your journey towards success in the Year 3 exam.
Importance of Multiply a 2-digit by a 1-digit number
The importance of Multiply a 2-digit by a 1-digit number cannot be overstated, especially for Year 3 aspirants.
This document holds the key to success in the Year 3 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Multiply a 2-digit by a 1-digit number Notes
Multiply a 2-digit by a 1-digit number Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Multiply a 2-digit by a 1-digit number.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Multiply a 2-digit by a 1-digit number Notes on EduRev are your ultimate resource for success.
Multiply a 2-digit by a 1-digit number Year 3 Questions
The "Multiply a 2-digit by a 1-digit number Year 3 Questions" guide is a valuable resource for all aspiring students preparing for the
Year 3 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Multiply a 2-digit by a 1-digit number on the App
Students of Year 3 can study Multiply a 2-digit by a 1-digit number alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Multiply a 2-digit by a 1-digit number,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Multiply a 2-digit by a 1-digit number is prepared as per the latest Year 3 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup