Mutual Inductance | Physics for Airmen Group X - Airforce X Y / Indian Navy SSR PDF Download
10. MUTUAL INDUCTANCE
Consider two coils P and S placed close to each other as shown in the figure. When the current passing through a coil increases or decreases, the magnetic flux linked with the other coil also changes and an induced e.m.f. is developed in it. This phenomenon is known as mutual induction. This coil in which current is passed is known as primary and the other in which e.m.f. is developed is called as secondary.
Let the current through the primary coil at any instant be i1. Then the magnetic flux 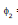 in the secondary at any time will be proportional to i1 i.e.,
in the secondary at any time will be proportional to i1 i.e., 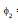 is directly proportional to i1
is directly proportional to i1
Therefore the induced e.m.f. in secondary
when i1 changes is given by
 i.e.,
i.e., 
 =
=  ⇒
⇒ 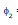 = M i1
= M i1 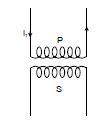
where M is the constant of proportionality and is known as mutual inductance of two coils. It is defined as the e.m.f. induced in the secondary coil by unit rate of change of current in the primary coil. The unit of mutual inductance is henry (H).
10.1 Mutual Inductance of a Pair of Solenoids one Surrounding the other coil
Figure shows a coil of N2 turns and radius R2 surrounding a long solenoid of length l1, radius R1 and number of turns N1.

To calculate mutual inductance M between them, let us assume a current i1 through the inner solenoid S1
There is no magnetic field outside the solenoid and the field inside has magnitude,

and is directed parallel to the solenoid's axis. The magnetic flux  through the surrounding coil is, therefore,
through the surrounding coil is, therefore,

Now, 
Notice that M is independent of the radius R2 of the surrounding coil. This is because solenoid's magnetic field is confined to its interior.
Brain Teaser
What is the meaning of the statement "The coefficient of mutual inductance for a pair of coils is large" ?
Note : 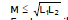
 For two coils in series if mutual inductance is considered then
For two coils in series if mutual inductance is considered then
Leq = L1 + L2 ± 2M
Ex.48 Find the mutual inductance of two concentric coils of radii a1 and a2 (a1 << a2) if the planes of coils are same.
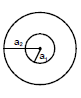
Sol. Let a current i flow in coil of radius a2.
Magnetic field at the centre of coil =
or M i =  or
or 
Ex.49 Solve the above question, if the planes of coil are perpendicular.
Sol. Let a current i flow in the coil of radius a1. The magnetic field at the centre of this coil will now be parallel to the plane of smaller coil and hence no flux will pass through it, hence M = 0
Ex.50 Solve the above problem if the planes of coils make θ angle with each other.
Sol. If i current flows in the larger coil, magnetic field produced at the centre will be perpendicular to the plane of larger coil.
Now the area vector of smaller coil which is perpendicular to the plane of smaller coil will make an angle θ with the magnetic field.
Thus flux =  . πa12 cos θ
. πa12 cos θ
or M = 
Ex.51 Find the mutual inductance between two rectangular loops, shown in figure.
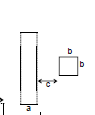
Sol. Let current i flow in the loop having ∞-by long sides. Consider a segment of width dx at a distance x as shown flux through the regent
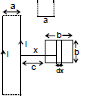
d =
= 
⇒  =
= 
= 
Ex.52 Figure shows two concentric coplanar coils with radii a and b (a << b). A current i = 2t flows in the smaller loop. Neglecting self inductance of larger loop
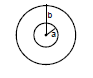
(a) Find the mutual inductance of the two coils
(b) Find the emf induced in the larger coil
(c) If the resistance of the larger loop is R find the current in it as a function of time
Sol. (a) To find mutual inductance, it does not matter in which coil we consider current and in which flux is calculated (Reciprocity theorem) Let current i be flowing in the larger coil. Magnetic field at the centre =  .
.
flux through the smaller coil = 
Therefore, M = 
(ii) |emf induced in larger coil| = 
=  =
= 
(iii) current in the larger coil = 
Ex.53 If the current in the inner loop changes according to i = 2t2 then, find the current in the capacitor as a function of time.
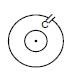
Sol. M = 
|emf induced in larger coil| = 
e =  =
= 
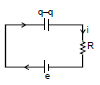
Applying KVL : -
+e -  - iR = 0 ⇒
- iR = 0 ⇒  - -iR = 0
- -iR = 0
differentiate wrt time :  -
-  -
-  on solving it i =
on solving it i = 
11. Series Combination of Inductors
 =
= 
Therefore, V = V1 + V2

Leθ = L1 + L2 +.................
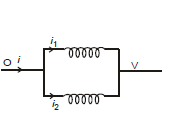
Parallel Combination of inductor
i = i1 + i2 ⇒ 


|
199 videos|422 docs|281 tests
|
FAQs on Mutual Inductance - Physics for Airmen Group X - Airforce X Y / Indian Navy SSR
| 1. What is mutual inductance? |  |
| 2. How is mutual inductance calculated? |  |
| 3. What are some real-life applications of mutual inductance? |  |
| 4. How does mutual inductance affect the efficiency of transformers? |  |
| 5. How does mutual inductance differ from self-inductance? |  |

|
Explore Courses for Airforce X Y / Indian Navy SSR exam
|

|

















