NCERT Exemplar: Conic Sections (Exercise) | Mathematics (Maths) for JEE Main & Advanced PDF Download
| Table of contents |

|
| Long Answer Type Questions |

|
| Objective Answer Type Questions |

|
| Fill in the Blanks |

|
| Multiple Choice Types Questions |

|
Short Answer Type Questions
Q.1: Find the equation of the circle which touches the both axes in first quadrant and whose radius is a.
Ans:
Clearly centre of the circle = (a, a)
and radius = a
Equation of circle with radius r and centre (h, k) is
(x – h)2 + (y – k)2 = r2
So, the equation of the required circle
⇒ (x – a)2 + (y – a)2 = a2
⇒ x2 – 2ax + a2 + y2 – 2ay + a2 = a2
⇒ x2 + y2 – 2ax – 2ay + a2 = 0
Hence, the required equation is
x2 + y2 – 2ax – 2ay + a2 = 0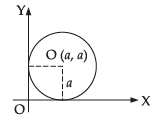
Q.2.:Show that the point (x, y) given by x =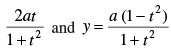 lies on a circle for all real values of t such that –1 ≤ t ≤ 1 where a is any given real numbers.
lies on a circle for all real values of t such that –1 ≤ t ≤ 1 where a is any given real numbers.
Ans:
Given
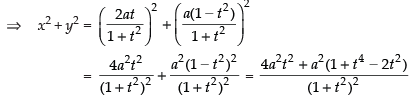
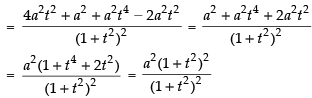
= a2
∴ x2 + y2 = a2 which is the equation of a circle.
Hence, the given points lie on a circle.
Q.3: If a circle passes through the point (0, 0) (a, 0), (0, b) then find the coordinates of its centre.
Ans:
Given points are (0, 0), (a, 0) and (0, b)
General equation of the circle is x2 + y2 + 2gx + 2fy + c = 0
where the centre is (– g, – f) and radius =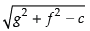
If it passes through (0, 0)
∴ c = 0
If it passes through (a, 0) and (0, b) then
a2 + 2ga + c = 0 ⇒ a2 + 2ga = 0 [∵ c = 0]
∴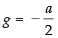
and 0 + b2 + 0 + 2fb + c = 0 ⇒ b2 + 2fb = 0 [∵ c = 0]
⇒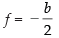
Hence, the coordinates of centre of the circle are (– g, – f)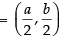
Q.4: Find the equation of the circle which touches x-axis and whose centre is (1, 2).
Ans: Since the circle whose centre is (1, 2) touch x-axis
∴ r = 2
So, the equation of the circle is
(x – h)2 + (y – k)2 = r2
⇒ (x – 1)2 + (y – 2)2 = (2)2
⇒ x2 – 2x + 1 + y2 – 4y + 4 = 4
⇒ x2 + y2 – 2x – 4y + 1 = 0
Hence, the required equation is
x2 + y2 – 2x – 4y + 1 = 0.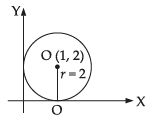
Q.5: If the lines 3x – 4y + 4 = 0 and 6x – 8y – 7 = 0 are tangents to a circle, then find the radius of the circle.
[Hint: Distance between given parallel lines gives the diameter of the circle.]
Ans: Given equation are 3x – 4y + 4 = 0
and 6x – 8y – 7 = 0 ⇒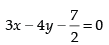
Since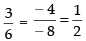 then the lines are parallel.
then the lines are parallel.
So, the distance between the parallel lines
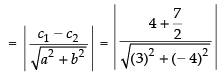
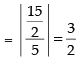
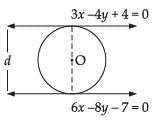
Diameter = 3/2
∴ Radius = 3/4
Hence, the required radius = 3/4.
Q.6. Find the equation of a circle which touches both the axes and the line 3x – 4y + 8 = 0 and lies in the third quadrant.
[Hint: Let a be the radius of the circle, then (– a, – a) will be centre and perpendicular distance from the centre to the given line gives the radius of the circle.]
Ans. Let a be the radius of the circle.
Centre of the circle = (– a, – a)
Distance of the line 3x – 4y + 8 = 0
From the centre = Radius of the circle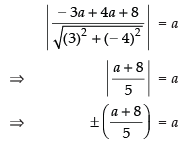
⇒
⇒ a = 5a – 8
⇒ 5a – a = 8
⇒ 4a = 8 ⇒ a = 2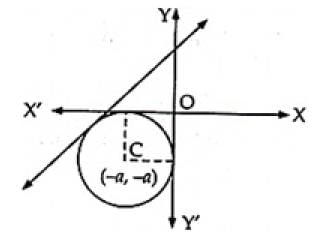
and
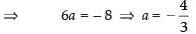
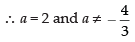
∴ The equation of the circle is
(x + 2)2 + (y + 2)2 = (2)2
⇒ x2 + 4x + 4 + y2 + 4y + 4 = 4
⇒ x2 + y2 + 4x + 4y + 4 = 0
Hence, the required equation of the circle
x2 + y2 + 4x + 4y + 4 = 0.
Q.7. If one end of a diameter of the circle x2 + y2 – 4x – 6y + 11 = 0 is (3, 4), then find the coordinate of the other end of the diameter.
Ans. Let the other end of the diameter is (x1, y1).
Equation of given circle is
x2 + y2 – 4x – 6y + 11 = 0
Centre = (– g, – f) = (2, 3)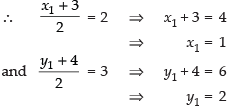
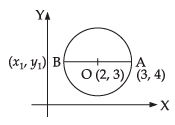
Hence, the required coordinates are (1, 2).
Q.8. Find the equation of the circle having (1, –2) as its centre and passing through 3x + y = 14, 2x + 5y = 18
Ans. Given equations are
3x + y = 14 ...(i)
and 2x + 5y = 18 ...(ii)
From eq. (i) we get y = 14 – 3x ...(iii)
Putting the value of y in eq. (ii) we get
⇒ 2x + 5(14 – 3x) = 18
⇒ 2x + 70 – 15x = 18
⇒ – 13x = – 70 + 18
⇒ – 13x = – 52
∴ x = 4
From eq. (iii) we get,
y = 14 – 3 x 4 = 2
∴ Point of intersection is (4, 2)
Now, radius r =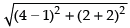
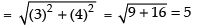
So, the equation of circle is (x – h)2 + (y – k)2 = r2
⇒ (x – 1)2 + ( + 2)2 = (5)2
⇒ x2 – 2x + 1 + y2 + 4y + 4 = 25
⇒ x2 + y2 – 2x + 4y – 20 = 0
Hence, the required equation is x2 + y2 – 2x + 4y – 20 = 0
Q.9. If the line y = √3x + k touches the circle x2 + y2 = 16, then find the value of k.
[Hint: Equate perpendicular distance from the centre of the circle to its radius].
Ans. Given circle is x2 + y2 = 16
Centre = (0, 0)
radius r = 4
Perpendicular from the origin to the given line y = √3x + k is equal to the radius.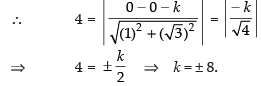
Hence, the required values of k are ± 8.
Q.10. Find the equation of a circle concentric with the circle x2 + y2 – 6x + 12y + 15 = 0 and has double of its area.
[Hint: concentric circles have the same centre.]
Ans. Given equation of the circle is
x2 + y2 – 6x + 12y + 15 = 0 ...(i)
Centre = (– g, – f) = (3, – 6)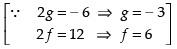
Since the circle is concentric with the given circle
∴ Centre = (3, – 6)
Now let the radius of the circle is r
∴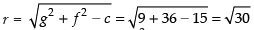
Area of the given circle (i) = πr2 = 30π sq unit
Area of the required circle = 2 x 30π = 60π sq. unit
If r1 be the radius of the required circle 2
πr12 = 60π ⇒ r21 = 60
So, the required equations of the circle is
(x - 3)2 + (y + 6)2 = 60
⇒ x2 + 9 - 6x + y2 + 36 + 12y - 60 = 0
⇒ x2 + y2 – 6x + 12y – 15 = 0
Hence, the required equation is x2 + y2 – 6x + 12y – 15 = 0.
Q.11. If the latus rectum of an ellipse is equal to half of minor axis, then find its eccentricity.
Ans. Let the equation of an ellipse is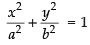
Length of major axis = 2a
Length of minor axis = 2b.
and the length of latus rectum =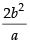
According to the question, we have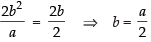
Now b2 = a2(1 – e2),
where e is the eccentricity
⇒ b2 = 4b2(1 – e2)
⇒ 1 = 4(1 – e2)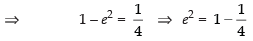
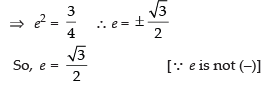
Hence, the required value of eccentricity is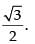
Q.12. Given the ellipse with equation 9x2 + 25y2 = 225, find the eccentricity and foci.
Ans. Given equation of ellipse is
9x2 + 25y2 = 225
⇒ 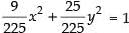
⇒ 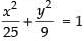
Here a = 5 and b = 3
b2 = a2(1 – e2)
⇒ 9 = 25(1 – e2)
⇒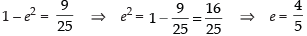
Now foci = (± ae, 0) =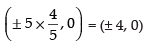
Hence, eccentricity =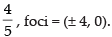
Q.13. If the eccentricity of an ellipse is 5/8 and the distance between its foci is 10, then find latus rectum of the ellipse.
Ans. Equation of an ellipse is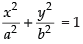
Eccentricity,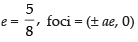
Distance between its foci = ae + ae = 2ae
∴ 2ae = 10
⇒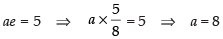
Now b2 = a2(1 – e2)
⇒ 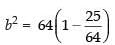
⇒ 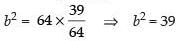
So, the length of the latus rectum = 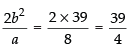
Hence, the length of the latus rectum = 39/4.
Q.14. Find the equation of ellipse whose eccentricity is 2/3, latus rectum is 5 and the centre is (0, 0).
Ans. Equations of ellipse is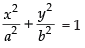 ....(i)
....(i)
Given that,e = 2/3
and latus rectum 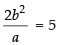
⇒ 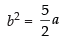 ...(ii)
...(ii)
We know that b2 = a2(1 – e2)
⇒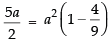
⇒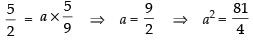
and
Hence, the required equation of ellipse is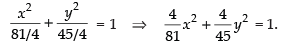
Q.15. Find the distance between the directrices of the ellipse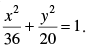
Ans. Given equation of ellipse is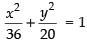
Here a2 = 36 ⇒ a = 6
b2 = 20 ⇒ b = 2 √5
We know that b2 = a2(1 – e2)
⇒ 20 = 36(1 – e2)
⇒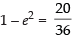
⇒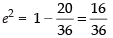
⇒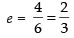
Now distance between the directrices is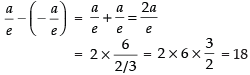
Hence, the required distance = 18.
Q.16. Find the coordinates of a point on the parabola y2 = 8x whose focal distance is 4.
Ans. Given parabola is y2 = 8x ...(i)
Comparing with the equation of parabola y2 = 4ax
4a = 8 ⇒ a = 2
Now focal distance =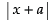
⇒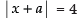
⇒ (x + a) = ± 4
⇒ x + 2 = ± 4
⇒ x = 4 – 2 = 2 and x = – 6
But x ≠ - 6 ∴ x = 2
Put x = 2 in equation (i) we get y2 = 8 x 2 = 16
∴ y = ± 4
So, the coordinates of the point are (2, 4), (2, – 4).
Hence, the required coordinates are (2, 4) and (2, – 4).
Q.17. Find the length of the line-segment joining the vertex of the parabola y2 = 4ax and a point on the parabola where the line-segment makes an angle θ to the xaxis.
Ans. Equation of parabola is y2 = 4ax
Let P(at2, 2at) be any point on the parabola.
In ΔPOA, we have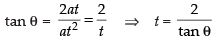
⇒ t = 2 cot θ ...(i)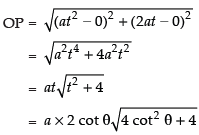
[∴ t = 2 cot θ]
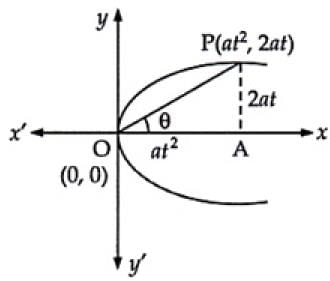
Hence, the required length =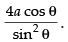
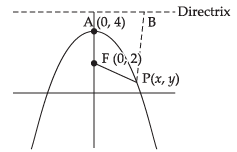
Q.18. If the points (0, 4) and (0, 2) are respectively the vertex and focus of a parabola, then find the equation of the parabola.
Ans. Given that: Vertex = (0, 4) and Focus = (0, 2)
Let P(x, y) be any point on the parabola. PB is perpendicular to the directrix.
According to the definition of parabola, we have
PF = PB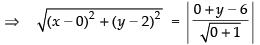
[Equation of directrix is y = 6]
Squaring both sides, we have
x2 + (y – 2)2 = (y – 6)2
⇒ x2 + y2 + 4 – 4y = y2 + 36 – 12y
⇒ x2 – 4y + 12y – 32 = 0
⇒ x2 + 8y – 32 = 0
Hence, the required equation is x2 + 8y = 32.
Q.19. If the line y = mx + 1 is tangent to the parabola y2 = 4x then find the value of m.
[Hint: Solving the equation of line and parabola, we obtain a quadratic equation and then apply the tangency condition giving the value of m]
Ans. Given that y2 = 4x ...(i)
and y = mx + 1 ...(ii)
From eq. (i) and (ii) we get
(mx + 1)2 = 4x
⇒ m2x2 + 1 + 2mx – 4x = 0
⇒ m2x2 + (2m – 4)x + 1 = 0
Applying condition of tangency, we have
(2m – 4)2 – 4m2 x 1 = 0
⇒ 4m2 + 16 - 16m - 4m2 = 0
⇒ – 16m = – 16
⇒ m = 1
Hence, the required value of m is 1.
Q.20. If the distance between the foci of a hyperbola is 16 and its eccentricity is √2 , then obtain the equation of the hyperbola.
Ans. Equation of hyperbola is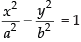
Distance between the foci = 2ae
2ae = 16 ⇒ ae = 8
⇒ a x √2 = 8
⇒ 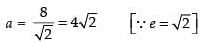
Now, b2 = a2(e2 – 1) [for hyperbola]
⇒ b2 = (4 √2)2 (2 - 1)
⇒ b2 = 32
a = 4√2 ⇒ a2 = 32
Hence, the required equation is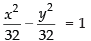
⇒ x2 – y2 = 32.
Q.21. Find the eccentricity of the hyperbola 9y2 – 4x2 = 36.
Ans. Given equation is 9y2 – 4x2 = 36
⇒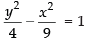
Clearly it is a vertical hyperbola .
Where a = 3 and b = 2
We know that b2 = a2(e2 – 1)
⇒ 4 = 9(e2 – 1)
⇒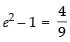
⇒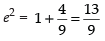
∴ 
Hence, the required value of e is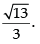
Q.22. Find the equation of the hyperbola with eccentricity 3/2 and foci at (± 2, 0).
Ans. Given that e = 3/2 and foci = (± 2, 0)
We know that foci = (± ae, 0)
∴ ae = 2
⇒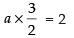
⇒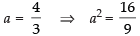
We know that b2 = a2(e2 – 1)
⇒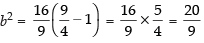
So, the equation of the hyperbola is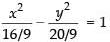
⇒ 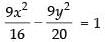
⇒ 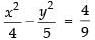
Hence, the required equation is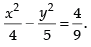
Long Answer Type Questions
Q.23. If the lines 2x – 3y = 5 and 3x – 4y = 7 are the diameters of a circle of area 154 square units, then obtain the equation of the circle.
Ans. We know that the intersection point of the diameter gives the centre of the circle.
Given equations of diameters are
2x – 3y = 5 ...(i)
3x – 4y = 7 ...(ii)
From eq. (i) we have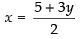 ...(iii)
...(iii)
Putting the value of x in eq. (ii) we have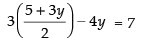
⇒ 15 + 9y – 8y = 14
⇒ y = 14 – 15 ⇒ y = – 1
Now from eq. (iii) we have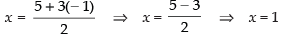
So, the centre of the circle = (1, – 1)
Given that area of the circle = 154
⇒ πr2 = 154
⇒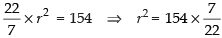
⇒ r2 = 7 x 7
⇒ r = 7
So, the equation of the circle is
(x – 1)2 + (y + 1)2 = (7)2
⇒ x2 + 1 – 2x + y2 + 1 + 2y = 49
⇒ x2 + y2 – 2x + 2y = 47
Hence, the required equation of the circle is
x2 + y2 – 2x + 2y = 47
Q.24. Find the equation of the circle which passes through the points (2, 3) and (4, 5) and the centre lies on the straight line y – 4x + 3 = 0.
Ans. Let the equation of the circle be
(x – h)2 + (y – k)2 = r2 ...(i)
If the circle passes through (2, 3) and (4, 5) then
(2 – h)2 + (3 – k)2 = r2 ...(ii)
and (4 – h)2 + (5 – k)2 = r2 ...(iii)
Subtracting eq. (iii) from eq. (ii) we have
(2 – h)2 – (4 – h)2 + (3 – k)2 – (5 – k)2 = 0
⇒ 4 + h2 - 4h - 16 - h2 + 8h + 9 + k2 - 6k - 25 - k2 + 10k = 0
⇒ 4h + 4k – 28 = 0
⇒ h + k = 7 ....(iv)
Since, the centre (h, k) lies on the line y – 4x + 3 = 0
then k – 4h + 3 = 0
⇒ k = 4h – 3
Putting the value of k in eq. (iv) we get
h + 4h – 3 = 7
⇒ 5h = 10 ⇒ h = 2
From (iv) we get k = 5
Putting the value of h and k in eq. (ii) we have
(2 – 2)2 + (3 – 5)2 = r2
⇒ r2 = 4
So, the equation of the circle is
(x – 2)2 + (y – 5)2 = 4
⇒ x2 + 4 – 4x + y2 + 25 – 10y = 4
⇒ x2 + y2 – 4x – 10y + 25 = 0
Hence, the required equation is
x2 + y2 – 4x – 10y + 25 = 0.
Q.25. Find the equation of a circle whose centre is (3, –1) and which cuts off a chord of length 6 units on the line 2x – 5y + 18 = 0.
[Hint: To determine the radius of the circle, find the perpendicular distance from the centre to the given line.]
Ans. Given that:
Centre of the circle = (3, – 1)
Length of chord AB = 6 units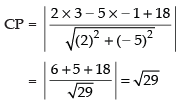

Now AB = 6 units.
∴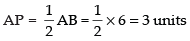
In ΔCPA, AC2 = CP2 + AP2
= (√29)2 + (3)2 = 29 + 9 = 38
∴ AC = √38
So, the radius of the circle, r = √38
∴ Equation of the circle is
(x – 3)2 + (y + 1)2 = (√38)2
⇒ (x – 3)2 + (y + 1)2 = 38
⇒ x2 + 9 – 6x + y2 + 1 + 2y = 38
⇒ x2 + y2 – 6x + 2y = 28
Hence, the required equation is x2 + y2 – 6x + 2y = 28.
Q.26. Find the equation of a circle of radius 5 which is touching another circle x2 + y2 – 2x – 4y – 20 = 0 at (5, 5).
Ans. Given circle is
x2 + y2 – 2x – 4y – 20 = 0
2g = – 2 ⇒ g = – 1
2f = – 4 ⇒ f = – 2
∴ Centre C1 = (1, 2)
and
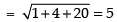
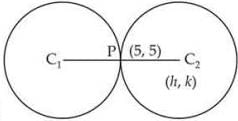
Let the centre of the required circle be (h, k).
Clearly, P is the mid-point of C1C2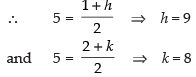
Radius of the required circle = 5
∴ Eq. of the circle is (x – 9)2 + (y – 8)2 = (5)2
⇒ x2 + 81 – 18x + y2 + 64 – 16y = 25
⇒ x2 + y2 – 18x – 16y + 145 – 25 = 0
⇒ x2 + y2 – 18x – 16y + 120 = 0
Hence, the required equation is x2 + y2 – 18x – 16y + 120 = 0.
Q.27. Find the equation of a circle passing through the point (7, 3) having radius 3 units and whose centre lies on the line y = x – 1.
Ans. Let the equation of the circle be
(x – h)2 + (y – k)2 = r2
If it passes through (7, 3) then
(7 – h)2 + (3 – k)2 = (3)2 [∵ r = 3]
⇒ 49 + h2 – 14h + 9 + k2 – 6k = 9
⇒ h2 + k2 – 14h – 6k + 49 = 0 ...(i)
If centre (h, k) lies on the line y = x – 1 then
k = h – 1 ...(ii)
Putting the value of k in eq. (i) we get
h2 + (h – 1)2 – 14h – 6(h – 1) + 49 = 0
⇒ h2 + h2 + 1 – 2h – 14h – 6h + 6 + 49 = 0
⇒ 2h2 – 22h + 56 = 0
⇒ h2 – 11h + 28 = 0
⇒ h2 – 7h – 4h + 28 = 0
⇒ h(h – 7) – 4(h – 7) = 0
⇒ (h – 4)(h – 7) = 0
∴ h = 4, h = 7
From eq. (ii) we get k = 4 – 1 = 3 and k = 7 – 1 = 6.
So, the centres are (4, 3) and (7, 6).
∴ Equation of the circle is
Taking centre (4, 3),
(x – 4)2 + (y – 3)2 = 9
x2 + 16 – 8x + y2 + 9 – 6y = 9
⇒ x2 + y2 – 8x – 6y + 16 = 0
Taking centre (7, 6)
(x – 7)2 + (y – 6)2 = 9
⇒ x2 + 49 – 14x + y2 + 36 – 12y = 9
⇒ x2 + y2 – 14x – 12y + 76 = 0
Hence, the required equations are
x2 + y2 – 8x – 6y + 16 = 0
and x2 + y2 – 14x – 12y + 76 = 0.
Q.28. Find the equation of each of the following parabolas
(a) Directrix x = 0, focus at (6, 0)
(b) Vertex at (0, 4), focus at (0, 2)
(c) Focus at (–1, –2), directrix x – 2y + 3 = 0
Ans.
(a) Given that directrix = 0 and focus (6, 0)
∴ The equation of the parabola is
(x – 6)2 + y2 = x2
⇒ x2 + 36 – 12x + y2 = x2
⇒ y2 – 12x + 36 = 0
Hence, the required equations is y2 – 12x + 36 = 0
(b) Given that vertex at (0, 4) and focus at (0, 2).
So, the equation of directrix is y – 6 = 0
According to the definition of the parabola
PF = PM.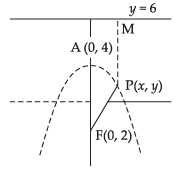
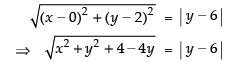
Squaring both the sides, we get
x2 + y2 + 4 – 4y = y2 + 36 – 12y
⇒ x2 + 4 – 4y = 36 – 12y
⇒ x2 + 8y – 32 = 0
⇒ x2 = 32 – 8y
Hence, the required equation is x2 = 32 – 8y.
(c) Given that focus at (– 1, – 2) and directrix x – 2y + 3 = 0
Let (x, y) be any point on the parabola.
According to the definition of the parabola, we have
PF = PM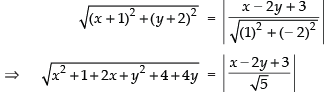
Squaring both sides, we get
x2 + 1 + 2x + y2 + 4 + 4y =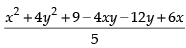
⇒ 5x2 + 5 + 10x + 5y2 + 20 + 20y
= x2 + 4y2 + 9 – 4xy – 12y + 6x
⇒ 4x2 + y2 + 4xy + 4x + 32y + 16 = 0
Hence, the required equation is
4x2 + 4xy + y2 + 4x + 32y + 16 = 0
Q.29. Find the equation of the set of all points the sum of whose distances from the points (3, 0) and (9, 0) is 12.
Ans. Let (x, y) be any point.
Given points are (3, 0) and (9, 0)
According to the question, we have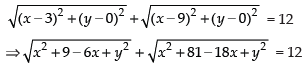
Putting x2 + 9 – 6x + y2 = k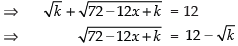
Squaring both sides, we have
⇒ 72 – 12x + k = 144 + k - 24√k
⇒ 24 √k = 144 – 72 + 12x
⇒ 24 √k = 72 + 12x
⇒ 2 √k = 6 + x
Again squaring both sides, we get
4k = 36 + x2 + 12x
Putting the value of k, we have
4(x2 + 9 – 6x + y2) = 36 + x2 + 12x
⇒ 4x2 + 36 – 24x + 4y2 = 36 + x2 + 12x
⇒ 3x2 + 4y2 – 36x = 0
Hence, the required equation is 3x2 + 4y2 – 36x = 0
Q.30. Find the equation of the set of all points whose distance from (0, 4) are 2/3 of their distance from the line y = 9.
Ans.
Let P(x, y) be a point.
According to question, we have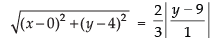
Squaring both sides, we have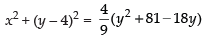
⇒ 9x2 + 9(y – 4)2 = 4y2 + 324 – 72y
⇒ 9x2 + 9y2 + 144 – 72y = 4y2 + 324 – 72y
⇒ 9x2 + 5y2 + 144 – 324 = 0
⇒ 9x2 + 5y2 – 180 = 0
Hence, the required equation is 9x2 + 5y2 – 180 = 0.
Q.31. Show that the set of all points such that the difference of their distances from (4, 0) and (– 4, 0) is always equal to 2 represent a hyperbola.
Ans. Let P(x, y) be any point.
According to the question, we have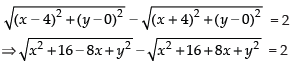
Putting the x2 + y2 + 16 = z ...(i)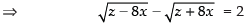
Squaring both sides, we get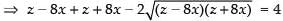
⇒ 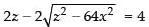
⇒ 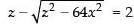
⇒ 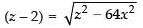
Again squaring both sides, we have
z2 + 4 – 4z = z2 – 64x2
⇒ 4 – 4z + 64x2 = 0
Putting the value of z, we have
⇒ 4 – 4(x2 + y2 + 16) + 64x2 = 0
⇒ 4 – 4x2 – 4y2 – 64 + 64x2 = 0
⇒ 60x2 – 4y2 – 60 = 0
⇒ 60x2 – 4y2 = 60
⇒ 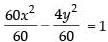
⇒ 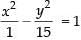
Which represent a hyperbola. Hence proved.
Q.32. Find the equation of the hyperbola with
(a) Vertices (± 5, 0), foci (± 7, 0)
(b) Vertices (0, ± 7), e = 4/3
(c) Foci (0, ± √10), passing through (2, 3)
Ans. (a) Given that vertices (± 5, 0), foci (± 7, 0)
Vertex of hyperbola = (± a, 0) and foci (± ae, 0)
∴ a = 5 and ae = 7 ⇒ 5 x e = 7 ⇒ e = 7/5
Now b2 = a2 (e2 – 1)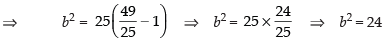
The equation of the hyperbola is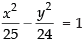
(b) Given that vertices (0, ± 7), e = 4/3
Clearly, the hyperbola is vertical.
Vertices = (± 0, a)
∴ a = 7 and e = 4/3
We know that b2 = a2(e2 – 1)
⇒ 
⇒ 
⇒ 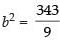
Hence, the equation of the hyperbola is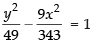
⇒ 9x2 – 7y2 + 343 = 0
(c) Given that: foci = (0 , ± √10)
∴ ae = √10 ⇒ a2e2 = 10
We know that b2 = a2(e2 – 1)
⇒ b2 = a2e2 – a2
⇒ b2 = 10 – a2
Equation of hyperbola is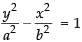
⇒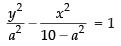
If it passes through the point (2, 3) then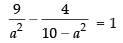
⇒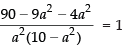
⇒ 90 – 13a2 = a2(10 – a2)
⇒ 90 – 13a2 = 10a2 – a4
⇒ a4 – 23a2 + 90 = 0
⇒ a4 – 18a2 – 5a2 + 90 = 0
⇒ a2(a2 – 18) – 5(a2 – 18) = 0
⇒ (a2 – 18)(a2 – 5) = 0
⇒ a2 = 18, a2 = 5
∴ b2 = 10 –18 = – 8 and b2 = 10 – 5 = 5
b ≠ – 8 ∴ b2 = 5
Here, the required equation is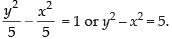
Objective Answer Type Questions
Q.33. The line x + 3y = 0 is a diameter of the circle x2 + y2 + 6x + 2y = 0.
Ans. Given equation of the circle is
x2 + y2 + 6x + 2y = 0
Centre is (– 3, – 1)
If x + 3y = 0 is the equation of diameter, then the centre (– 3, – 1) will lie on x + 3y = 0
– 3 + 3(– 1) = 0
⇒ – 6 ≠ 0
So, x + 3y = 0 is not the diameter of the circle.
Hence, the given statement is False.
Q.34. The shortest distance from the point (2, –7) to the circle x2 + y2 – 14x – 10y – 151 = 0 is equal to 5.
[Hint: The shortest distance is equal to the difference of the radius and the distance between the centre and the given point.]
Ans. Given equation of circle is x2 + y2 – 14x – 10y – 151 = 0
Shortest distance = distance between the point (2, – 7)
and the centre – radius of the circle
Centre of the given circle is
2g = – 14 ⇒ g = – 7
2f = – 10 ⇒ f = – 5
∴ Centre = (– g, – f) = (7, 5)
and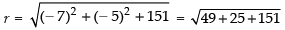
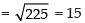
∴ Shortest distance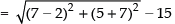
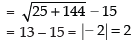
Hence, the given statement is False.
Q.35. If the line lx + my = 1 is a tangent to the circle x2 + y2 = a2, then the point (l, m) lies on a circle.
[Hint: Use that distance from the centre of the circle to the given line is equal to radius of the circle.]
Ans. Given equation of circle is x2 + y2 = a2
and the tangent is lx + my = 1
Here centre is (0, 0) and radius = a
If (l, m) lies on the circle
∴ 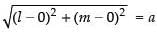
⇒ 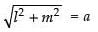
⇒ l2 + m2 = a2 (which is a circle)
So, the point (l, m) lies on the circle.
Hence, the given statement is True.
Q.36. The point (1, 2) lies inside the circle x2 + y2 – 2x + 6y + 1 = 0.
Ans. Given equation of circle is x2 + y2 – 2x + 6y + 1 = 0
Here 2g = – 2 ⇒ g = – 1
2f = 6 ⇒ f = 3
∴ Centre = (– g, – f) = (1, – 3)
and 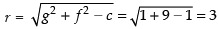
∴ Distance between the point (1, 2) and the centre (1, – 3)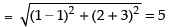
Here 5 > 3, so the point lies out side the circle.
Hence, the given statement is False.
Q.37. The line lx + my + n = 0 will touch the parabola y2 = 4ax if ln = am2.
Ans. Given equation of parabola is y2 = 4ax ...(i)
and the equation of line is lx + my + n = 0 ...(ii)
From eq. (ii), we have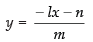
Putting the value of y in eq. (i) we get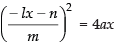
⇒ l2x2 + n2 + 2lnx – 4am2x = 0
⇒ l2x2 + (2ln – 4am2)x + n2 = 0
If the line is the tangent to the circle, then
b2 – 4ac = 0
(2ln – 4am2)2 – 4l2n2 = 0
⇒ 4l2n2 + 16a2m4 – 16lnm2a – 4l2n2 = 0
⇒ 16a2m4 – 16lnm2a = 0
⇒ 16am2(am2 – ln) = 0
⇒ am2(am2 – ln) = 0
⇒ am2 ≠ 0 ∴ am2 - ln = 0
∴ ln = am2
Hence, the given statement is True.
Q.38. If P is a point on the ellipse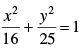 whose foci are S and S′, then PS + PS′ = 8.
whose foci are S and S′, then PS + PS′ = 8.
Ans. Let P(x1, y1) be a point on the ellipse. foci = (± ae, 0)
Here a2 = 25 ⇒ a = 5
b2 = 16 ⇒ b = 4
b2 = a2(1 – e2)
16 = 25(1 – e2)
⇒ 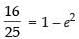
⇒ 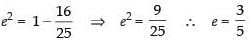
∴ 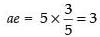
So, the foci are S(3, 0) and S’(- 3, 0).
Since PS + PS’ = 2a = 2 x 5 = 10.
Hence, the given statement is False.
Q.39. The line 2x + 3y = 12 touches the ellipse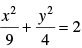 at the point (3, 2).
at the point (3, 2).
Ans. If line 2x + 3y = 12 touches the ellipse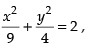 then the point (3, 2) satisfies both line and ellipse.
then the point (3, 2) satisfies both line and ellipse.
∴ For line 2x + 3y = 12
2(3) + 3(2) = 12
6 + 6 = 12
12 = 12 True
For ellipse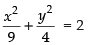
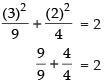
1 + 1 = 2
2 = 2 True
Hence, the given statement is True.
Q.40. The locus of the point of intersection of lines √3 x − y − 4 √3k = 0 and
√3kx + ky – 4√3 = 0 for different value of k is a hyperbola whose eccentricity is 2.
[Hint:Eliminate k between the given equations]
Ans. The given equations are
√3x - y - 4 √3k = 0 ...(i)
and √3kx + ky - 4 √3 = 0 ...(ii)
From eq. (i) we get
4√3k = √3x - y
∴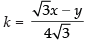
Putting the value of k in eq. (ii), we get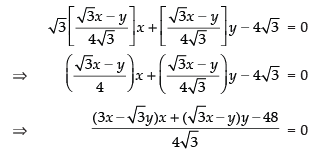
⇒ 3x2 - √3xy + √3xy - y2 - 48 = 0
⇒ 3x2 – y2 = 48
⇒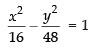 which is a hyperbola.
which is a hyperbola.
Here a2 = 16, b2 = 48
We know that b2 = a2(e2 – 1)
⇒ 48 = 16(e2 – 1)
⇒ 3 = e2 – 1
⇒ e2 = 4 ⇒ e = 2
Hence, the given statement is True.
Fill in the Blanks
Q.41. The equation of the circle having centre at (3, – 4) and touching the line 5x + 12y – 12 = 0 is _______.
[Hint: To determine radius find the perpendicular distance from the centre of the circle to the line.]
Ans. Given equation of the line is 5x + 12y – 12 = 0 and the centre is (3, – 4)
CP = radius of the circle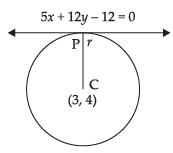
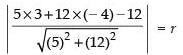
⇒ 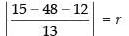
⇒ 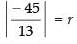
⇒ 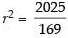
So, the equation of the circle is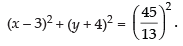
Hence, the value of the filler is (x – 3)2 + (y + 4)2 = 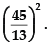
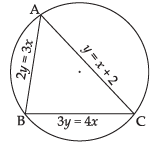
Q.42. The equation of the circle circumscribing the triangle whose sides are the lines y = x + 2, 3y = 4x, 2y = 3x is _______ .
Ans. Let AB represents 2y = 3x ...(i)
BC represents 3y = 4x ...(ii)
and AC represents y = x + 2 ...(iii)
From eq. (i) and (ii)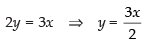
Putting the value of y in eq. (ii) we get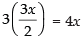
⇒ 9x = 8x
⇒ x = 0 and y = 0
∴ Coordinates of B = (0, 0)
From eq. (i) and (iii) we get
y = x + 2
Putting y = x + 2 in eq. (i) we get
2(x + 2) = 3x
⇒ 2x + 4 = 3x
⇒ x = 4 and y = 6
∴ Coordinates of A = (4, 6)
Solving eq. (ii) and (iii) we get
y = x + 2
Putting the value of y in eq. (ii) we get
3(x + 2) = 4x ⇒ 3x + 6 = 4x ⇒ x = 6 and y = 8
∴ Coordinates of C = (6, 8)
It implies that the circle is passing through (0, 0), (4, 6) and (6, 8).
We know that the general equation of the circle is
x2 + y2 + 2gx + 2fy + c = 0 ...(i)
Since the points (0, 0), (4, 6) and (6, 8) lie on the circle then
0 + 0 + 0 + 0 + c = 0 ⇒ c = 0
⇒ 16 + 36 + 8g + 12f + c = 0
⇒ 8g + 12f + 0 = – 52
⇒ 2g + 3f = – 13 ...(ii)
and 36 + 64 + 12g + 16f + c = 0
⇒ 12g + 16f + 0 = – 100
⇒ 3g + 4f = – 25 ...(iii)
Solving eq. (ii) and (iii) we get
2g + 3f = – 13
3g + 4f = – 25
⇒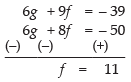
Putting the value of f in eq. (ii) we get
2g + 3 x 11 = - 13
⇒ 2g + 33 = – 13
⇒ 2g = – 46 ⇒ g = – 23
Putting the values of g, f and c in eq. (i) we get
x2 + y2 + 2(– 23)x + 2(11)y + 0 = 0
⇒ x2 + y2 – 46x + 22y = 0
Hence, the value of the filler is x2 + y2 – 46x + 22y = 0.
Q.43. An ellipse is described by using an endless string which is passed over two pins. If the axes are 6 cm and 4 cm, the length of the string and distance between the pins are _______.
Ans. Let equation of ellipse is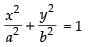
Here 2a = 6 ⇒ a = 3
and 2b = 4 ⇒ b = 2
We know that c2 = a2 – b2
= (3)2 – (2)2 = 9 – 4 = 5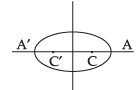
∴
Length of string = 2a + 2ae = 2a(1 + e)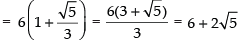
Distance between the pins = CC’ = 2ae =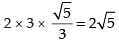
Hence the value of the filler are 6 + 2√5 cm and 2√5 cm.
Q.44. The equation of the ellipse having foci (0, 1), (0, –1) and minor axis of length 1 is_______.
Ans. We know that the foci of the ellipse are (0, ± ae) and given foci are (0, ± 1), so ae = 1
Length of minor axis = 2b = 1 ⇒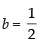
We know that b2 = a2(1 – e2)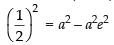
⇒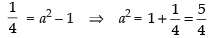
∴ Equation of ellipse is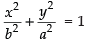
⇒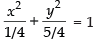
⇒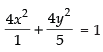
Hence, the value of the filler is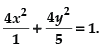
Q.45. The equation of the parabola having focus at (–1, –2) and the directrix x – 2y + 3 = 0 is ________.
Ans. Let (x1, y1) be any point on the parabola.
According to the definition of the parabola
Squaring both sides, we get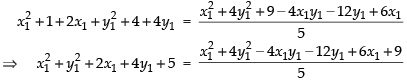
⇒ 5x12 + 5y12 + 10x1 + 20 y1 + 25
= x21 + 4 y12 - 4x1 y1 - 12 y1 + 6x1 + 9
⇒ 4 x12 + y12 + 4 x1 + 32 y1 + 4 x1 y1 + 16 = 0
Hence, the value of the filler is 4x2 + 4xy + y2 + 4x + 32y + 16 = 0.
Q.46. The equation of the hyperbola with vertices at (0, ± 6) and eccentricity 5/3 is________and its foci are _______ .
Ans. Let equation of the hyperbola is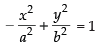
Vertices are (0, ± b) ∴ b = 6 and e = 5/3
We know that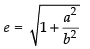
⇒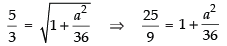
⇒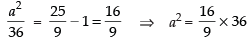
⇒ a2 = 64
So the equation of the hyperbola is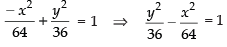
and foci = (0, ± be) =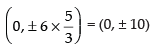
Hence, the value of the filler is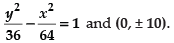
Multiple Choice Types Questions
Choose the correct answer out of the given four options (M.C.Q.)
Q.47. The area of the circle centred at (1, 2) and passing through (4, 6) is
(a) 5 π
(b) 10π
(c) 25π
(d) None of these
Ans. (c)
Solution.
Given that the centre of the circle is (1, 2)
Radius of the circle =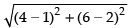
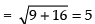
So, the area of the circle = πr2
= π x (5)2 = 25π
Hence, the correct option is (c).
Q.48. Equation of a circle which passes through (3, 6) and touches the axes is
(a) x2 + y2 + 6x + 6y + 3 = 0
(b) x2 + y2 – 6x – 6y – 9 = 0
(c) x2 + y2 – 6x – 6y + 9 = 0
(d) None of these
Ans. (c)
Solution.
Let the required circle touch the axes at (a, 0) and (0, a)
∴ Centre is (a, a) and r = a
So the equation of the circle is (x – a)2 + (y – a)2 = a2
If it passes through a point P(3, 6) then
(3 – a)2 + (6 – a)2 = a2
⇒ 9 + a2 – 6a + 36 + a2 – 12a = a2
⇒ a2 – 18a + 45 = 0
⇒ a2 – 15a – 3a + 45 = 0
⇒ a(a – 15) – 3(a – 15) = 0
⇒ (a – 3) (a – 15) = 0
⇒ a = 3 and a = 15 which is not possible
∴ a = 3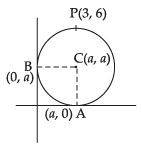
So, the required equation of the circle is
(x – 3)2 + (y – 3)2 = 9
⇒ x2 + 9 – 6x + y2 + 9 – 6y = 9
⇒ x2 + y2 – 6x – 6y + 9 = 0
Hence, the correct option is (c).
Q.49. Equation of the circle with centre on the y-axis and passing through the origin and the point (2, 3) is
(a) x2 + y2 + 13y = 0
(b) 3x2 + 3y2 + 13x + 3 = 0
(c) 6x2 + 6y2 – 13x = 0
(d) x2 + y2 + 13x + 3 = 0
Ans. (a)
Solution.
Let the equation of the circle be
(x – h)2 + (y – k)2 = r2
Let the centre be (0, a)
∴ Radius r = a
So, the equation of the circle is
(x – 0)2 + (y – a)2 = a2
⇒ x2 + (y – a)2 = a2
⇒ x2 + y2 + a2 – 2ay = a2
⇒ x2 + y2 – 2ay = 0 ...(i)
Now CP = r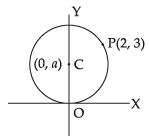
⇒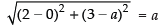
⇒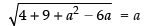
⇒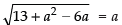
⇒ 13 + a2 – 6a = a2
⇒ 13 – 6a = 0
∴ a = 13/6
Putting the value of a in eq. (i) we get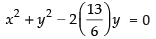
⇒ 3x2 + 3y2 – 13y = 0
(Note: (a) option is correct and it should be 3x2 + 3y2 – 13y = 0)
Hence, the correct option is (a).
Q.50. The equation of a circle with origin as centre and passing through the vertices of an equilateral triangle whose median is of length 3a is
(a) x2 + y2 = 9a2
(b) x2 + y2 = 16a2
(c) x2 + y2 = 4a2
(d) x2 + y2 = a2
[Hint: Centroid of the triangle coincides with the centre of the circle and the radius of the circle is 2/3 of the length of the median]
Ans. (c)
Solution.
Let ABC be an equilateral triangle in which median AD = 3a.
Centre of the circle is same as the centroid of the triangle i.e., (0, 0)
AG : GD = 2 : 1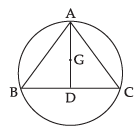
So, 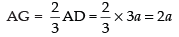
∴ The equation of the circle is
(x – 0)2 + (y – 0)2 = (2a)2
⇒ x2 + y2 = 4a2
Hence, the correct option is (c).
Q.51. If the focus of a parabola is (0, –3) and its directrix is y = 3, then its equation is
(a) x2 = –12y
(b) x2 = 12y
(c) y2 = –12x
(d) y2 = 12x
Ans. (a)
Solution.
According to the definition of parabola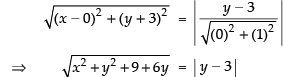
Squaring both sides, we have
x2 + y2 + 9 + 6y = y2 + 9 – 6y
⇒ x2 + 9 + 6y = 9 – 6y
⇒ x2 = – 12y
Hence, the correct option is (a).
Q.52. If the parabola y2 = 4ax passes through the point (3, 2), then the length of its latus rectum is
(a) 2/3
(b) 4/3
(c) 1/3
(d) 4
Ans. (b)
Solution.
Given parabola is y2 = 4ax
If the parabola is passing through (3, 2) then
(2)2 = 4a x 3
⇒ 4 = 12a ⇒ a = 1/3
Now length of the latus rectum = 4a =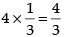
Hence, the correct option is (b).
Q.53. If the vertex of the parabola is the point (– 3, 0) and the directrix is the line x + 5 = 0, then the equation is
(a) y2 = 8(x + 3)
(b) x2 = 8(y + 3)
(c) y2 = – 8(x + 3)
(d) y2 = 8(x + 5)
Ans. (a)
Solution.
Given that vertex = (– 3, 0)
∴ a = – 3
and directrix is x + 5 = 0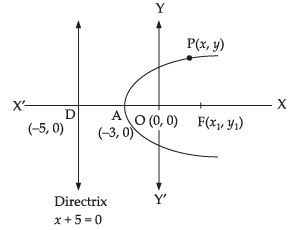
According to the definition of the parabola, we get
AF = AD i.e., A is the mid-point of DF
∴ 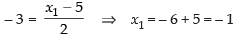
and 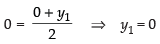
∴ Focus F = (– 1, 0)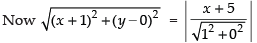
Squaring both sides, we get
(x + 1)2 + y2 = (x + 5)2
⇒ x2 + 1 + 2x + y2 = x2 + 25 + 10x
⇒ y2 = 10x – 2x + 24 ⇒ y2 = 8x + 24
⇒ y2 = 8(x + 3)
Hence, the correct option is (a).
Q.54. The equation of the ellipse, whose focus is (1, – 1), the directrix the line x – y – 3 = 0 and eccentricity 1/2, is
(a) 7x2 + 2xy + 7y2 – 10x + 10y + 7 = 0
(b) 7x2 + 2xy + 7y2 + 7 = 0
(c) 7x2 + 2xy + 7y2 + 10x – 10y – 7 = 0
(d) None of the above
Ans. (a)
Solution.
Given that focus of the ellipse is (1, – 1) and the equation of the directrix is x – y – 3 = 0 and e = 1/2.
Let P(x, y) by any point on the parabola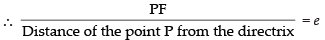
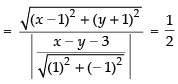
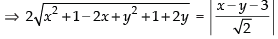
Squaring both sides, we have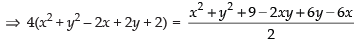
⇒ 8x2 + 8y2 – 16x + 16y + 16 = x2 + y2 – 2xy + 6y – 6x + 9
⇒ 7x2 + 7y2 + 2xy – 10x + 10y + 7 = 0
Hence, the correct option is (a).
Q.55. The length of the latus rectum of the ellipse 3x2 + y2 = 12 is
(a) 4
(b) 3
(c) 8
(d) 4√3
Ans. (d)
Solution.
Equation of the ellipse is
3x2 + y2 = 12
⇒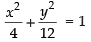
Here a2 = 4 ⇒ a = 2
b2 = 12 ⇒ b = 2√ 3
Length of the latus rectum =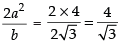
Hence, the correct option is (d).
Q.56. If e is the eccentricity of the ellipse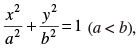 then
then
(a) b2 = a2(1 – e2)
(b) a2 = b2(1 – e2)
(c) a2 = b2(e2 – 1)
(d) b2 = a2(e2 – 1)
Ans. (b)
Solution.
Given equation is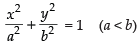
∴Eccentricity e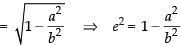
⇒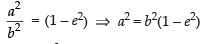
Hence, the correct option is (b).
Q.57. The eccentricity of the hyperbola whose latus rectum is 8 and conjugate axis is equal to half of the distance between the foci is
(a) 4/3
(b) 4/√3
(c) 2/√3
(d) None of these
Ans. (c)
Solution.
Length of the latus rectum of the hyperbola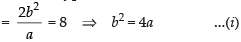
Distance between the foci = 2ae
Transverse axis = 2a
and Conjugate axis = 2b
∴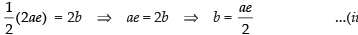 )
)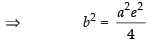
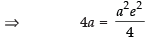 [from eq. (i)]
[from eq. (i)]
⇒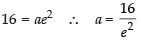
Now b2 = a2(e2 – 1)
⇒ 4a = a2(e2 – 1)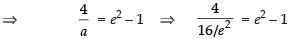
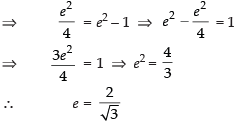
Hence, the correct option is (c).
Q.58. The distance between the foci of a hyperbola is 16 and its eccentricity is 2 . Its equation is
(a) x2 – y2 = 32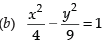
(c) 2x2 – 3y2 = 7
(d) None of these
Ans. (a)
Solution.
We know that the distance between the foci = 2ae
∴ 2ae = 16 ⇒ ae = 8
Given that e = √2
∴ 2a = 8 ⇒ a = 4 √2
Now b2 = a2(e2 – 1)
⇒ b2 = 32(2 – 1)
⇒ b2 = 32
So, the equation of the hyperbola is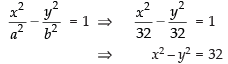
Hence, the correct option is (a).
Q.59. Equation of the hyperbola with eccentricty 3/2 and foci at (± 2, 0) is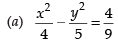
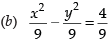
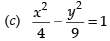
(d) None of these
Ans. (a)
Solution.
Given that e = 3/2
and foci = (± ae, 0) = (± 2, 0)
∴ ae = 2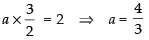
Now we know that b2 = a2(e2 – 1)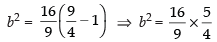
⇒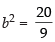
So, the equation of the hyperbola is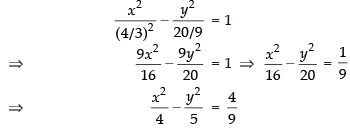
Hence, the correct option is (a).
|
172 videos|476 docs|154 tests
|
FAQs on NCERT Exemplar: Conic Sections (Exercise) - Mathematics (Maths) for JEE Main & Advanced
| 1. What are the different types of conic sections? |  |
| 2. How are conic sections used in real-life applications? |  |
| 3. What is the general equation of a conic section? |  |
| 4. How are conic sections related to the focus and directrix of a curve? |  |
| 5. How can conic sections be used to solve geometric problems? |  |





















