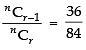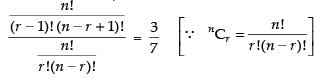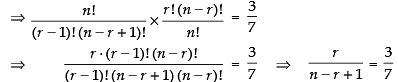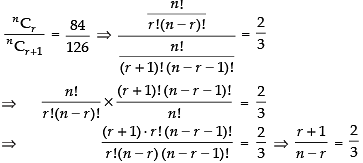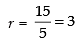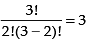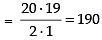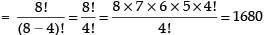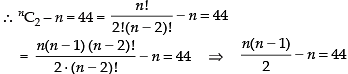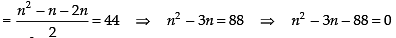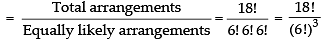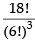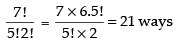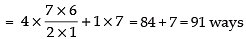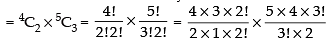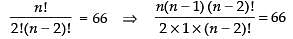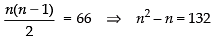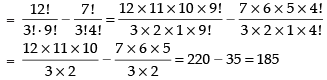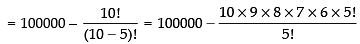NCERT Exemplar: Permutations and Combinations:
Short Answer Type Questions
Q.1. Eight chairs are numbered 1 to 8. Two women and 3 men wish to occupy one chair each. First the women choose the chairs from amongst the chairs 1 to 4 and then men select from the remaining chairs. Find the total number of possible arrangements.
[Hint: 2 women occupy the chair, from 1 to 4 in 4P2 ways and 3 men occupy the remaining chairs in 6P3 ways.]
Ans.
We have 2 women and 3 men
First women choose the chairs amongst the chairs 1 to 4
i.e. total number of chairs = 4
So, the number of arrangements = 4P2 ways
Now 3 men choose from the remaining 6 chairs
So, the number of arrangements = 6P3 ways
∴ Total number of arrangements = 4P2 x 6P3

Hence, the total number of possible arrangements are 1440.
Q.2. If the letters of the word RACHIT are arranged in all possible ways as listed in dictionary. Then what is the rank of the word RACHIT ? [Hint: In each case number of words beginning with A, C, H, I is 5!]
Ans.
The alphabetical order of RACHIT is A, C, H, I, R and T
Number of words beginning with A = 5!
Number of words beginning with C = 5!
Number of words beginning with H = 5!
Number of words beginning with I = 5!
and Number of word beginning with R i.e. RACHIT = 1
∴ The rank of the word ‘RACHIT’ in the dictionary
= 5! + 5! + 5! + 5! + 1 = 4 x 5! + 1
= 4 x 5 . 4 . 3 . 2 . 1 + 1 = 4 x 120 + 1 = 480 + 1 = 481
Q.3. A candidate is required to answer 7 questions out of 12 questions, which are divided into two groups, each containing 6 questions. He is not permitted to attempt more than 5 questions from either group. Find the number of different ways of doing questions.
Ans.
Total number of questions = 12
Number of questions in each group = 6
7 questions are to be attempted but not more than 5 questions from either group
∴ Total number of ways = 6C5 x 6C2 + 6C4 x 6C3 + 6C3 x 6C4 + 6C2 x 6C5
= 2[6C5 x 6C2 + 6C4 x 6C3]

2[6 x 15 + 15 x 20] = 2[90 + 300] = 2 x 390 = 780
Hence, the total number of ways = 780
Q.4. Out of 18 points in a plane, no three are in the same line except five points which are collinear. Find the number of lines that can be formed joining the point.
[Hint: Number of straight lines = 18C2 – 5C2 + 1.]
Ans.
Total number of points = 18
Out of 18 numbers, 5 are collinear and we get a straight line by joining any two points.
∴ Total number of straight line formed by joining 2 points out of 18 points = 18C2
Number of straight lines formed by joining 2 points out of 5 points = 5C2
But 5 points are collinear and we get only one line when they are joined pairwise.
So, the required number of straight lines are

Hence, the total number of straight lines = 144.
Q.5. We wish to select 6 persons from 8, but if the person A is chosen, then B must be chosen. In how many ways can selections be made?
Ans.
Total number of persons = 8
Number of persons to be selected = 6
Condition is that if A is chosen, B must be chosen
Case I: When A is chosen, B must be chosen
Number of ways = 6C4 [∵ A and B are set to be chosen]
Case II: When A is not chosen, then B may be chosen
∴ Number of ways = 7C6
So, the total number of ways = 6C4 + 7C6
[∴ There are two cases]
= 6C2 + 7C1 [nCr = nCn-r]

Hence, the required number of ways = 22.
Q.6. How many committee of five persons with a chairperson can be selected from 12 persons.
[Hint: Chairman can be selected in 12 ways and remaining in 11C4.]
Ans.
Total number of Persons = 12
Number of persons to be selected = 5
Out of 5, there is a chairperson
∴ Number of ways of selecting a chairperson = 12C1 = 12
Number of ways of selecting other 4 numbers out of remaining 11 persons = 11C4
∴ Total number of ways = 12C1 x 11C4

Hence, the required number of ways = 3960.
Q.7. How many automobile license plates can be made if each plate contains two different letters followed by three different digits?
Ans.
We have 26 English alphabet and 10 digits (0 to 9)
Since, it is given that each plate contains 2 different letters followed by 3 different digits.
∴ Number of arrangement of 26 letters taken 2 at a time

Three digit number can be formed out of 10 digit = 10P3

∴ Total number of license plates = 650 x 720 = 468000
Hence, the required number of plates = 468000.
Q.8. A bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red balls can be selected from the lot.
Ans.
Given that bag contains 5 black and 6 red balls.
Number of ways of selecting 2 black balls out of 5 black balls = 5C2
And number of ways of selecting 3 red balls out of 6 red balls = 6C3
∴ Total number of ways of selecting 2 black and 3 red balls = 5C2 x 6C3

Hence, the required ways of selecting the balls = 200.
Q.9. Find the number of permutations of n distinct things taken r together, in which 3 particular things must occur together.
Ans.
Total number of things = n 3 things must be together
∴ The number of remaining things = n - 3
Number of things to be selected = r
Out of r, 3 are always together
∴ Number of ways of selection = n-3Cr-2
Now permutation of 3 things which are always together = 3!
Number of permutations of (r – 2) things = (r – 2)!
∴ Total number of arrangements = n-3Cr-2 x(r - 2)! x 3!
Hence the required arrangements = n–3Cr–2 x (r - 2)! x 3!
Q.10. Find the number of different words that can be formed from the letters of the word ‘TRIANGLE’ so that no vowels are together.
Ans.
Total number of words in ‘TRIANGLE’ = 8
Out of 5 are consonants and 3 are vowels
If vowels are not together, taken we have the following arrangement
V | C | V | C | V | C | V | C | V | C | V
Consonant can be arranged in 5! = 120 ways
Vowel occupy 6 places
∴ 3 vowels can be arranged in 6 places = 6P3

So, the total arrangement = 120 x 120 = 14400 ways
Here, the required arrangement = 14400 ways.
Q.11. Find the number of positive integers greater than 6000 and less than 7000 which are divisible by 5, provided that no digit is to be repeated.
Ans.
Any number divisible by 5, its unit place must have 0 or 5
We have to find 4-digit number greater than 6000 and less than 7000.
So, the unit place can be filled with 2 ways (0 or 5) since, repetition is not allowed
∴ Tens place can be filled with 7 ways and hundreds place can be filled with 8 ways.
But the required number is greater than 6000 and less than 7000. So, thousand place can be filled with 1 digits i.e.6

So, the total number of integers = 1 x 8 x 7 x 2 = 112
Hence, the required number of integers = 112
Q.12. There are 10 persons named P1, P2, P3, ... P10. Out of 10 persons, 5 persons are to be arranged in a line such that in each arrangement P1 must occur whereas P4 and P5 do not occur. Find the number of such possible arrangements.
[Hint: Required number of arrangement = 7C4 × 5!]
Ans.
Given that P1, P2, P3, P4, … P10 are 10 persons out of which 5 persons are to be arranged but P1 must occur and P4 and P5 never occur
∴ selection is to be done only for 10 - 3 = 7 persons
∴ Number of selection = 7C4 =

5 people can be arranged as 5!
So, the number of arrangement = 35 x 5! = 35 x 120 = 4200
Hence, the required arrangement = 4200.
Q.13. There are 10 lamps in a hall. Each one of them can be switched on independently. Find the number of ways in which the hall can be illuminated.
[Hint: Required number = 210 – 1].
Ans.
Total number of lamps = 10
The total number of ways in which hall can be illuminated is equal to the number of selection of one or more items out of n different items.
i.e. nC1 + nC2 + nC3 + nC4 + … + nCn = 2n – 1
From Binomial expansion, we have
nC0 + nC1 + nC2 + … + nCn = 2n
So total number of ways = 10C1 + 10C2 + 10C3 + … + 10C10
= 210 – 1 = 1024 – 1 = 1023
Hence, the required number of possible ways = 1023.
Q.14. A box contains two white, three black and four red balls. In how many ways can three balls be drawn from the box, if atleast one black ball is to be included in the draw.
[Hint: Required number of ways = 3C1 × 6C2 + 3C2 × 6C2 + 3C3.]
Ans.
We have 2 white, 3 black and 4 red balls in a box. 3 balls are to be drawn out of 9 balls atleast one black ball is to be included
So, the possible selection is
(1 black and 2 other balls) or (2 black and 1 other ball) or (3 black and no other ball)
So, the number of possible selection is
= 3C1 x 6C2 + 3C2 x 6C1 + 3C3 x 6C0
= 3 x 15 + 3 x 6 + 1 x 1 = 45 + 18 + 1 = 64
Hence, the required selection = 64.
Q.15. If nCr – 1 = 36, nCr = 84 and nCr + 1 = 126, then find rC2.
[Hint: Form equation using to find the value of r.]
to find the value of r.]
Ans.
Given that nCr – 1 = 36 ...(i)
nCr = 84 ……(ii)
nCr + 1 = 126 ……(iii)
Dividing eq. (i) by. (ii) we get

⇒ 

⇒ 3n – 3r + 3 = 7r ⇒ 3n - 10r = - 3 ...(iv)
Now dividing eq. (ii) by eq. (iii), we get

⇒ 2n – 2r = 3r + 3 ⇒ 2n - 5r = 3 ...(v)
Solving eq. (iv) and (v) we have

⇒ 2 x 9 - 5r = 3 ⇒ 18 - 5r = 3
⇒ 
So rC2 = 3C2 = 
Hence, the value of rC2 = 3
Q.16. Find the number of integers greater than 7000 that can be formed with the digits 3, 5, 7, 8 and 9 where no digits are repeated.
[Hint: Besides 4 digit integers greater than 7000, five digit integers are always greater than 7000.]
Ans.
Given that all the 5 digit numbers are greater than 7000.
So, the ways of forming 5-digit numbers = 5 x 4 x 3 x 2 x 1 = 120
Now all the four digit number greater than 7000 can be formed as follows.
Thousand place can be filled with 3 ways
Hundred place can be filled with 4 ways
Tenths place can be filled with 3 ways
Units place can be filled with 2 ways
So, the total number of 4-digits numbers = 3 x 4 x 3 x 2 = 72
∴ Total number of integers = 120 + 72 = 192
Hence, the required number of integers = 192
Q.17. If 20 lines are drawn in a plane such that no two of them are parallel and no three are concurrent, in how many points will they intersect each other?
Ans.
Given that out of 20 lines, no two lines are parallel and no three lines are concurrent.
Therefore, number of point of intersection
= 20C2 [∴ for any point of intersection, we need two lines]

Hence, the required number of points = 190.
Q.18. In a certain city, all telephone numbers have six digits, the first two digits always being 41 or 42 or 46 or 62 or 64. How many telephone numbers have all six digits distinct?
Ans.
If first two digits is 41, then the remaining 4 digits can be arranged in 8P4 ways

Similarly first two digits can be 42 or 46 or 62 or 64.
∴ Total number of telephone numbers have all digits distinct = 5 x 1680 = 8400
Hence, the required telephone numbers = 8400
Q.19. In an examination, a student has to answer 4 questions out of 5 questions; questions 1 and 2 are however compulsory. Determine the number of ways in which the student can make the choice.
Ans.
Given that question number 1 and 2 are compulsory.
∴ The remaining questions are 5 - 2 = 3
Total number of questions to be attempted = 4 questions 1 and 2 are compulsory
So only 2 questions are to be done out of 3 questions Therefore number of ways = 3C2 = 3C3-2 = 3C1 = 3
[∴ nCr = nCn-r]
Hence, the required number of ways = 3.
Q.20. A convex polygon has 44 diagonals. Find the number of its sides.
[Hint: Polygon of n sides has (nC2 – n) number of diagonals.]
Ans.
Let n be the number of sides in a polygon.
Since, Polygon of n sides has (nC2 – n) number of diagonals


= n2 – 11n + 8n – 88 = 0 ⇒ n(n – 11) + 8(n – 11) = 0
= (n – 11) (n + 8) = 0 ∴ n = 11 and n = – 8 [∵ n ≠ - 8]
So n = 11
Hence, the required number of sides = 11.
Long Answer Type Questions
Q.21. 18 mice were placed in two experimental groups and one control group, with all groups equally large. In how many ways can the mice be placed into three groups?
Ans.
Given that 18 mice were placed equally in two experimental groups and one control group i.e. 3 groups
∴ The required number of arrangements

Hence, the required arrangements =
Q.22. A bag contains six white marbles and five red marbles. Find the number of ways in which four marbles can be drawn from the bag if
(a) they can be of any colour
(b) two must be white and two red and
(c) they must all be of the same colour.
Ans.
Total number of marbles = 6 white + 5 red = 11 marbles
(i) Since, we have to draw 4 marbles of any colour from the 11 marbels
∴ Required number of ways = 11C4
(ii) If 2 must be white and 2 must be red,
then the required number of ways = 6C2 x 5C2
(iii) If all the 4 marbles are of the same colour,
then, the required number of ways = 6C4 + 5C4
Hence the required number of ways are
(i) 11C4 (ii) 6C2 x 5C2 (iii) 6C4 + 5C4
Q.23. In how many ways can a football team of 11 players be selected from 16 players? How many of them will
(i) include 2 particular players?
(ii) exclude 2 particular players?
Ans.
Given that the total number of players = 16 We have to select 11 players out of 16 players. (i) If 2 players are included,
then then number of ways of selection = 16 – 2C11 – 2 = 14C9
(ii) If 2 players are excluded,
then the number of ways of selection = 16 – 2C11 = 14C11
Hence, the required number of ways of selection
(i) 14C9 (ii) 14C11
Q.24. A sports team of 11 students is to be constituted, choosing at least 5 from Class XI and atleast 5 from Class XII. If there are 20 students in each of these classes, in how many ways can the team be constituted?
Ans.
Total number of students in each class = 20
We have to select atleast 5 students from each class.
We have the following cases.
(i) 5 students from XI class and 6 students from XII class
(ii) 6 students from XI class and 5 students from XII class
So, number of ways of selection of a team of 11 players = 20C5 x 20C6 + 20C6 x 20C5
= 2[20C5 x 20C6]
Hence, the required ways of selection = 2[20C5 x 20C6]
Q.25. A group consists of 4 girls and 7 boys. In how many ways can a team of 5 members be selected if the team has
(i) no girls
(ii) at least one boy and one girl
(iii) at least three girls.
Ans.
We have 4 girls and 7 boys and a team of 5 members is to be selected.
(i) If no girl is selected, then all the 5 members are to be selected out of 7 boys
i.e. 7C5 =
(ii) When at least one by and one girl are to be selected, then
Number of ways = 4C1 x 7C4 + 4C2 x 7C3 + 4C3 x 7C2 + 4C4 x 7C1

= 4 x 35 + 6 x 35 + 4 x 21 + 7 = 140 + 210 + 84 + 7 = 441
ways
(iii) When atleast 3 girls are included, then
Number of ways = 4C3 x 7C2 + 4C4 x 7C1

Hence the required number of ways are
(i) 21 ways (ii) 441 ways (iii) 91 ways
Objective Type Questions
Q.26. If nC12 = nC8, then n is equal to
(A) 20
(B) 12
(C) 6
(D) 30
Ans.
Given that nC12 = nC8 [∴ nCr = nCn – r]
nC12 = nCn-8
∴ n – 8 = 12 ⇒ n = 12 + 8 = 20
Hence, the correct option is (a)
Q.27. The number of possible outcomes when a coin is tossed 6 times is
(A) 36
(B) 64
(C) 12
(D) 32
Ans.
We know that a coin has Head and Tail (H, T)
∴ When a coin is tossed 6 times, then the
Possible outcome = 26 = 64
Hence, the correct option is (b).
Q.28. The number of different four digit numbers that can be formed with the digits 2, 3, 4, 7 and using each digit only once is
(A) 120
(B) 96
(C) 24
(D) 100
Ans.
Four-digit numbers are to be formed from the digits 2, 3, 4, 7 without repetition
So, the required 4-digit numbers = 4P4 = 4! = 4 x 3 x 2 x 1 = 24
Hence, the correct option is (c).
Q.29. The sum of the digits in unit place of all the numbers formed with the help of 3, 4, 5 and 6 taken all at a time is
(A) 432
(B) 108
(C) 36
(D) 18
Ans.
If we fix 3 at unit place, then the total possible numbers = 3!
If we fix 4, 5 and 6 at unit place, this is each case, total possible numbers are 3!
Required sum of unit digits of all such numbers is
= 3 x 3! + 4 x 3! + 5 x 3! + 6 x 3! = (3 + 4 + 5 + 6) x 3!
= 18 x 3! = 18 x 3 x 2 x 1 = 108
Hence, the correct option is (b).
Q.30. Total number of words formed by 2 vowels and 3 consonants taken from 4 vowels and 5 consonants is equal to
(A) 60
(B) 120
(C) 7200
(D) 720
Ans.
Given that total numbers of vowels = 4
and total numbers of consonants = 5
Total number of words formed by 2 vowels and 3 consonants

= 6 x 10 = 60
Now permutation of 2 vowels and 3 consonants = 5!
= 5 x 4 x 3 x 2 x 1 = 120
So, the total number of words = 60 x 120 = 7200.
Hence, the correct option is (c).
Q.31. A five digit number divisible by 3 is to be formed using the numbers 0, 1, 2, 3, 4 and 5 without repetitions. The total number of ways this can be done is (A) 216
(B) 600
(C) 240
(D) 3125
[Hint: 5 digit numbers can be formed using digits 0, 1, 2, 4, 5 or by using digits 1, 2, 3, 4, 5 since sum of digits in these cases is divisible by 3.]
Ans.
We know that a number is divisible by 3 when the sum of its digits is divisible by 3.
If we take the digits 0, 1, 2, 4, 5, then the sum of the digits
= 0 + 1 + 2 + 4 + 5 = 12 which is divisible by 3
So, the 5 digit numbers using the digits 0, 1, 2, 4, and 5

4 x 4 x 3 x 2 x 1 = 96
and if we take the digits 1, 2, 3, 4, 5, then their sum
= 1 + 2 + 3 + 4 + 5 = 15 divisible by 3
So, five digit numbers can be formed using the digits 1, 2, 3, 4, 5 is 5! ways = 5 x 4 x 3 x 2 x 1 = 120 ways
Total number of ways = 96 + 120 = 216
Hence, the correct option is (a).
Q.32. Every body in a room shakes hands with everybody else. The total number of hand shakes is 66. The total number of persons in the room is
(A) 11
(B) 12
(C) 13
(D) 14
Ans.
Let the total number of persons in a room be n since, two persons make 1 hand shake
∴ The number of hand shakes = nC2
So nC2 = 66
⇒ 
⇒ 
⇒ n2 – n – 132 = 0 ⇒ n2 – 12n + 11n – 132 = 0
⇒ n(n – 12) + 11 (n – 12) = 0 ⇒ (n - 12) (n + 11) = 0
⇒ n – 12 = 0, n + 11 = 0⇒ n = 12, n = – 11
∴ n = 12 (∴ n ≠ - 11)
Hence, the correct option is (b).
Q.33. The number of triangles that are formed by choosing the vertices from a set of 12 points, seven of which lie on the same line is
(A) 105
(B) 15
(C) 175
(D) 185
Ans.
Total number of triangles formed from 12 points taking 3 at a time = 12C3
But given that out of 12 points, 7 are collinear
So, these seven points will form no triangle.
∴ The required number of triangles = 12C3 - 7C3

Hence, the correct option is (d).
Q.34. The number of parallelograms that can be formed from a set of four parallel lines intersecting another set of three parallel lines is
(A) 6
(B) 18
(C) 12
(D) 9
Ans.
We know that to form a parallelogram, we require a pair of lines from a set of 4 lines and another pair of lines from another set of 3 lines
∴ Required numbers of parallelograms = 4C2 x 3C2 = 6 x 3 = 18
Hence, the correct option is (b).
Q.35. The number of ways in which a team of eleven players can be selected from 22 players always including 2 of them and excluding 4 of them is
(A) 16C11
(B) 16C5
C) 16C9
(D) 20C9
Ans.
Total number of players = 22
2 players are always included and 4 are always excluding or never included = 22 – 2 – 4 = 16
∴ Required number of selection = 16C9
Hence, the correct option is (c).
Q.36. The number of 5-digit telephone numbers having atleast one of their digits repeated is
(A) 90,000
(B) 10,000
(C) 30,240
(D) 69,760
Ans.
Total number of 5-digit telephone number if all the digits are repeated = (10)5 [Q digits are from 0 to 9]
If digits are not repeated, then 5-digit telephones, can be formed in 10P5 ways
∴ Required number of ways =(10)5 - 10P5

= 100000 – 30240 = 69760
Hence, the correct option is (d).
Q.37. The number of ways in which we can choose a committee from four men and six women so that the committee includes at least two men and exactly twice as many women as men is
(A) 94
(B) 126
(C) 128
(D) None
Ans.
Number of men = 4
Number of women = 6
We are given that the committee includes 2 men and exactly twice as many women as men.
Thus, the possible selection can be 2 men and 4 women and 3 men and 6 women.
So, the number of committee = 4C2 x 6C4 + 4C3 x 6C6
= 6 x 15 + 4 x 1 = 90 + 4 = 94
Hence, the correct option is (a).
Q.38. The total number of 9 digit numbers which have all different digits is
(A) 10!
(B) 9 !
(C) 9 × 9!
(D) 10×10!
Ans.
We have to form 9 digit numbers from 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
and we know that 0 can not be put on extremely left place.
So, first place from the left can be filled in 9 ways.
Now repetition is not allowed. So, the remaining 8 places can be filled in 9!
∴ The required number of ways = 9 x 9!
Hence, the correct option is (c).
Q.39. The number of words which can be formed out of the letters of the word ARTICLE, so that vowels occupy the even place is
(A) 1440
(B) 144
(C) 7!
(D) 4C4 × 3C3
Ans.
Total number of letters in the ‘ARTICLE’ is 7 out which A, E, I are vowels and R, T, C, L are consonants
Given that vowels occupy even place
∴ possible arrangement can be shown as below
C, V, C, V, C, V, C i.e. on 2nd , 4th and 6th places
Therefore, number of arrangement = 3P3 = 3! = 6 ways
Now consonants can be placed at 1, 3, 5 and 7th place
∴ Number of arrangement = 4P4 = 4! = 24
So, the total number of arrangements = 6 x 24 = 144
Hence, the correct option is (b).
Q.40. Given 5 different green dyes, four different blue dyes and three different red dyes, the number of combinations of dyes which can be chosen taking at least one green and one blue dye is
(A) 3600
(B) 3720
(C) 3800
(D) 3600
[Hint: Possible numbers of choosing or not choosing 5 green dyes, 4 blue dyes and 3 red dyes are 25, 24 and 23, respectively.]
Ans.
Possible number of choosing 5 different green dyes = 25
Possible number of choosing 4 blue dyes = 24
and possible number of choosing 3 red dyes = 23
If atleast one blue and one green dyes are selected then the
total number of selection = (25 – 1) x (24 - 1) x 23 = 31 x 15 x 8 = 3720
Hence, the correct option is (b).





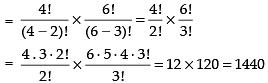
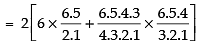
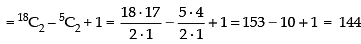
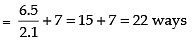

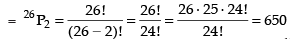
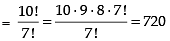
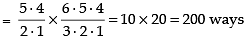
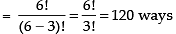
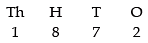
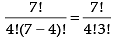
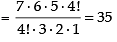
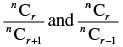 to find the value of r.]
to find the value of r.]