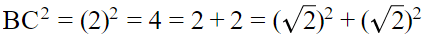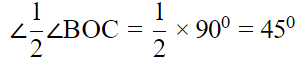NCERT Exemplar Solutions: Circles | Mathematics (Maths) Class 9 PDF Download

Q.1. AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is:
(a) 17 cm
(b) 15 cm
(c) 4 cm
(d) 8 cm

Correct Answer is Option (d)
Given: Diameter of the circle = d = AD = 34 cm
∴ Radius of the circle = r = d / 2 = AO = 17 cm
Length of chord AB = 30 cm
Since the line drawn through the center of a circle to bisect a chord is perpendicular to the chord, therefore AOP is a right angled triangle with L as the bisector of AB.
∴ AP = 1 / 2(AB) = 15 cm
In right angled triangle AOB, by Pythagoras theorem, we have:
(AO)² = (OP)² + (AP)²
⇒ (17)² = (OP)² + (15)²
⇒ (OP)² = (17)² – (15)²
⇒ (OP)² = 289 – 225
⇒ (OP)² = 64
Take square root on both sides:
⇒ (OP) = 8
∴ The distance of AB from the center of the circle is 8 cm.
Hence, option (d) is the correct answer.

Q.2. In Fig. 10.3, if OA = 5 cm, AB = 8 cm and OD is perpendicular to AB, then CD is equal to:
(a) 2 cm
(b) 3 cm
(c) 4 cm
(d) 5 cm

Correct Answer is Option (a)
Given:
Radius of the circle = r = AO = 5 cm
Length of chord AB = 8 cm
Since the line drawn through the center of a circle to bisect a chord is perpendicular to the chord, therefore AOC is a right angled triangle with C as the bisector of AB.
∴ AC = ½ (AB) = 8 / 2 = 4 cm
In right angled triangle AOC, by Pythagoras theorem, we have:
(AO)² = (OC)² + (AC)²
⇒ (5)² = (OC)² + (4)²
⇒ (OC)² = (5)² – (4)²
⇒ (OC)² = 25 – 16
⇒ (OC)² = 9
Take square root on both sides:
⇒ (OC) = 3
∴ The distance of AC from the center of the circle is 3 cm.
Now, OD is the radius of the circle, ∴ OD = 5 cm
CD = OD – OC
CD = 5 – 3
CD = 2
Therefore, CD = 2 cm
Hence, option (a) is the correct answer.

Q.3. If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is:
(a) 6 cm
(b) 8 cm
(c) 10 cm
(d) 12 cm

Correct Answer is Option (c)
According to the question,
AB = 12 cm, BC = 16 cm, AB ⊥ BC.
Therefore,
AC is the diameter of the circle passing through the points A, B and C.
Now, according to the figure,
We get,
ABC is a right angled triangle.
By Pythagoras theorem:
(AC)² = (CB)² + (AB)²
⇒ (AC)² = (16)² + (12)²
⇒ (AC)² = 256 + 144
⇒ (AC)² = 400
Take square root on LHS and RHS,
We get,
(AC) = 20
Diameter of the circle = 20 cm
Thus, radius of the circle = Diameter / 2
= 20 / 2
= 10 cm
Hence, Radius of the circle = 10 cm
Hence, option (c) is the correct answer.

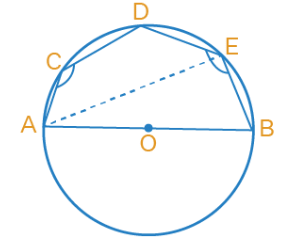
Q.4. In Fig.10.4, if ∠ABC = 20º, then ∠AOC is equal to:
(a) 20º
(b) 40º
(c) 60º
(d) 10º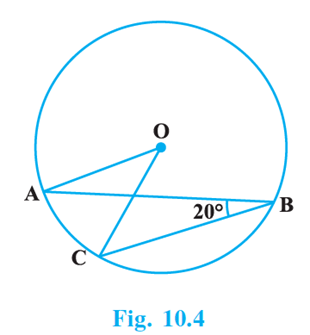

Correct Answer is Option (b)
According to the question,
∠ABC = 20°
We know that,
“The angle subtended by an arc at the center of a circle is twice the angle subtended by it at remaining part of the circle”
According to the theorem, we have,
∠AOC = 2 × ∠ABC
= 2 × 20°
= 40°
Therefore, ∠AOC = 40°
Hence, option (b) is the correct answer.

Q.5. In Fig.10.5, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to:
(a) 30º
(b) 60º
(c) 90º
(d) 45º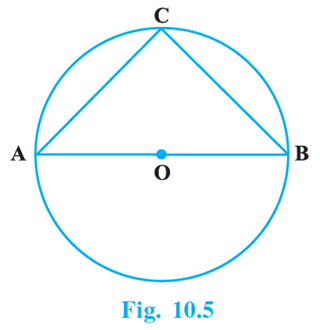

Correct Answer is Option (d)
According to the question,
We have,
Diameter of the circle = AOB
AC = BC
Since, angles opposite to equal sides are equal
∠ABC = ∠BAC
Let, ∠ABC = ∠BAC = x
Also, diameter subtends a right angle to the circle,
∠ACB = 90°
We also know that,
By angle sum property of a triangle, sum of all angles of a triangle = 180°.
∠CAB + ∠ABC + ∠ACB = 180°
⇒ x + x + 90° = 180°
⇒ 2x = 90°
⇒ x = 45°
∠CAB = ∠ ABC = 45°
Hence, option (d) is the correct answer.

Q.6. In Fig. 10.6, if ∠OAB = 40º, then ∠ACB is equal to:

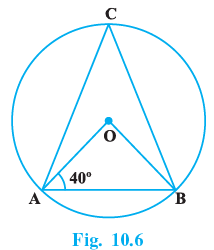
(a) 50º
(b) 40º
(c) 60º
(d) 70°

Correct Answer is Option (a)
Given: ∠OAB = 40º
Now, in triangle OAB,
OA = OB   .....[Radii of circle]
So, ∠OAB = ∠OBA = 40º  ......[Angle opposite to equal sides are equal]
So, ∠AOB = 180º – (40º + 40º)
= 100º
As we know that angle subtended by an arc of a circle at the center is double the angle subtended by it at any point on the remaining part of the circle.
So, ∠ACB = 1/2 ∠AOB = 1/2 × 100 = 50º

Q.7. In Fig. 10.7, if ∠DAB = 60º, ∠ABD = 50º, then ∠ACB is equal to: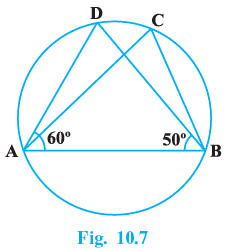

(a) 60º
(b) 50º
(c) 70º
(d) 80º

Correct Answer is Option (c)

In △ADC, we have
∠DAC = 60° and ∠ABD = 50°
By angle sum property, in △ABD
∠DAB + ∠ABD + ∠ADB = 180°
⇒ 60° + 50° + ∠ADB = 180°
⇒ ∠ADB = 180° − 110°
⇒∠ADB = 70°
We know that the angles subtended at the circumference by the same arc are equal.

∴ ∠ADB = ∠ACB

⇒ ∠ACB = 70°

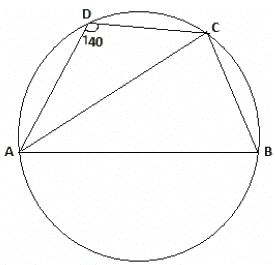
Q.8. ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to:
(a) 80º
(b) 50º
(c) 40º
(d) 30º

Correct Answer is Option (b)
Given:
ABCD is a cyclic quadrilateral with AB as the diameter of the circle.
Also, ∠ADC = 140°. 

We have to find: ∠BAC.
Then,
∠ADC + ∠ABC = 180°  ....(since the sum of the opposite angles of a quadrilateral is 180°).

∴∠ABC = 180° −140° = 40°.
Also, ∠ACB = 90°....(since the angle subtended by a diameter at the circumference of the circle, is 90°).
∴ In ΔABC we have,
∠ACB = 90° and ∠ABC = 40°. 

So, ∠CAB = 180° −(∠ACB + ∠ABC) =180° − (90° +40°)
∴∠BAC = 50°.
Hence, option (b) is correct.

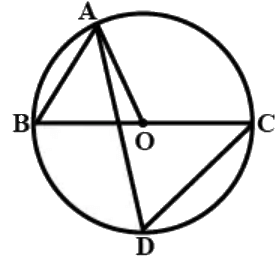
Q.9. In Fig. 10.8, BC is a diameter of the circle and ∠BAO = 60º. Then ∠ADC is equal to :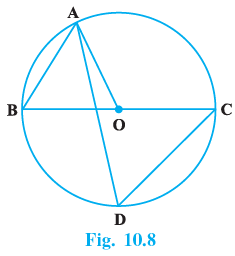

(a) 30º
(b) 45º
(c) 60º
(d) 120º

Correct Answer is Option (c)
In △AOB,
OA = OB
⇒ ∠OAB = ∠OBA = 60°
We know that the exterior angle of a triangle is equal to sum of the two opposite angles of the triangle.
∠AOC = ∠OAB + ∠OBA
∠AOC= 60° + 60°

∠AOC = 120°

We know that the angle subtended at the centre of the circle by an arch is twice the angle subtended at the circumference by the same arc.
∴∠ADC = (1/2)∠AOC
= 120/2 = 60°

Q.10. In Fig. 10.9, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to: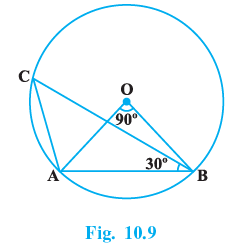

(a) 30º
(b) 45º
(c) 90º
(d) 60º

Correct Answer is Option (d)
In △AOB
OA = OB
∴ ∠OAB + ∠OBA + ∠AOB = 180°

⇒ 2∠OAB + 90° = 180°
⇒ 2∠OAB = 180° − 90°  = 90°

⇒ 2∠OAB = (90/2) = 45°

We know that the angle subtended at the centre of the circle by an arch is twice the angle subtended at the circumference by the same arc.

∴∠ACB = (1/2) ∠AOB
(90/2) = 45°
Again in △ABC
∠ACB + ∠CBA + ∠BAC = 180°
⇒ 45° + 30° + ∠BAC = 180°
⇒ ∠BAC = 180° − 75° = 105°
∴ ∠CAO = ∠BAC − ∠OAB
⇒ ∠CAO = 105° − 45° = 60°

Write True or False and justify your answer in each of the following:
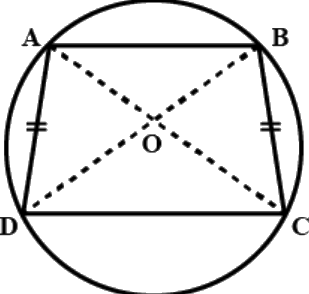
Q.1. Two chords AB and CD of a circle are each at distances 4 cm from the centre. Then AB = CD.

True
Given that AB and AC are chords that are at a distance of 4 cm from center of a circle.
Since, chords that are equidistant from the center of a circle are equal in length,
We have, AB = CD.

Q.2. Two chords AB and AC of a circle with centre O are on the opposite sides of OA. Then ∠OAB = ∠OAC .

False
Let AB and AC be the chord of the circle with center O on the opposite side of OA.
Consider the triangles AOC and AOB:
AO = AO (Common side in both triangles)
OB = OC (Both OB and OC are radius of circle)
But we can’t show that either the third side of both triangles are equal or any angle is equal. Therefore ΔAOB is not congruent to ΔAOC.
∴ ∠OAB ≠ ∠OAC.

Q.3. Two congruent circles with centres O and O’ intersect at two points A and B. Then ∠AOB = ∠AO’B.

True
Equal chords of congruent circles subtend equal angles at the respective centre.
Hence, the given statement is true.

Q.4. Through three collinear points a circle can be drawn.

False
A circle through two points cannot pass through a point which is collinear to these two points.
Hence, the given statement is false.

Q.5. A circle of radius 3 cm can be drawn through two points A, B such that AB = 6 cm.

True
According to the question,
Radius of circle = 3 cm
Diameter of circle = 2 × r
= 2 × 3 cm
= 6 cm
Now, From the question we have,
AB = 6 cm
So, the given statement is true because AB will be the diameter.

Q.6. If AOB is a diameter of a circle and C is a point on the circle, then AC² + BC² = AB².

True
Angle subtended by the diameter at the circumference of a circle is one right angle. 

AOB is diameter and C is a point on the circle.
∠ACB = 90°
Using Pythagoras Theorem, we have
AC² + BC² = AB²

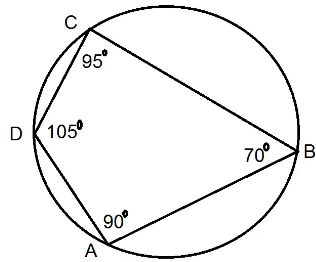
Q.7. ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.

False
Given, ABCD is a cyclic quadrilateral where ∠A = 90°, ∠B = 70°, ∠C = 95°  & ∠D = 105°.
Since ABCD is a cyclic quadrilateral, then ∠A + ∠C = 180°  and ∠B + ∠D = 180° ...(i)
(The sum of the opposite angles of a cyclic quadrilateral is 180°)
But here, ∠A+∠C = 90° + 95°  =185° and ∠B+∠D = 70° + 105° = 175°.
This is a contradiction to (i).

That is, the statement is false.

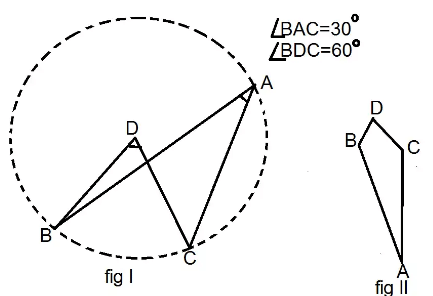
Q.8. If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.

True

Now, we know the theorem 

The angle which an are of a circle 

Subtends at the center is double which 

it subtends at any point on the 

remaining part of the circumference.

Hence according to the above theorem

∠BOC = 2∠BAC

Now, 

∠BDC = 60° [Given]

= 2 × 30°  

∠BDC = 2 × ∠BAC [∵ ∠BAC = 30° Given]

Hence, from the above theorem, we can say that D is the center of the circle through A, B and C

Q.9. If A, B, C and D are four points such that ∠BAC = 45° and ∠BDC = 45°, then A, B, C, D are concyclic.

True
In geometry, a set of points are said to be concyclic if they lie on a common circle.
Given  ∠BAC = 45° and ∠BDC = 45°
From the figure, it can be seen that they are lying on the circumference of the circle by same chord BC.
But from the theorem we also know that, the angle subtended by the chord at the circle are equal .
Here angles are equal , which means that these 4 points are concyclic .
∴  A, B, C, D are concyclic.

Q.10. In Fig. 10.10, if AOB is a diameter and ∠ADC = 120°, then ∠CAB = 30°.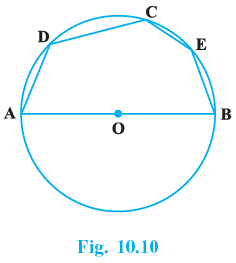

True
Given−
AOB is the diameter of the circle with centre O.
ADCEB is a polygon inscribed in the circle.
∠ADC = 120°
To find out−

the validity of the assumption that ∠CAB = 30°.
Solution−
BC is joined.
Now ∠ACB has been subtended by the diameter AB to the circumference at C.
∴ ∠ACB =90°. (the angle subtended by the diameter of a circle to its centre = 90°).

Again ABCD is a cyclic quardrilateral.
∴ ∠ADC + ∠ABC = 180°
⇒ ∠ABC = 180° − 120° = 60°.

(the sum of the opposite angles of a cyclic quadrilateral is = 180°).
So in ΔABC we have ∠CAB = 180° −(∠ACB + ∠ABC)=180° − (90° + 60°) = 30°.

∴ The given assumption is true.

Q.1. If arcs AXB and CYD of a circle are congruent, find the ratio of AB and CD.

According to the question,
We have,
AXB ≅ CYD.
We know that,
If two arcs of a circle are congruent, then their corresponding arcs are also equal.
So, we have chord AB = chord CD.
Hence, we get,
AB / CD = 1
AB / CD = 1 / 1
AB : CD = 1 : 1.

Q.2. If the perpendicular bisector of a chord AB of a circle PXAQBY intersects the circle at P and Q, prove that arc PXA ∠ Arc PYB.

According to the question,
We have,
PQ is the perpendicular bisect of AB,
So, we get,
AM = BM …eq.(1)
In △APM and △BPM,
From eq.(1),
AM = BM
∠AMP = ∠BMP = 90º
PM = PM [Common side]
Therefore, △APM ≅ △BPM [By SAS congruence rule]
So, AP = BP [CPCT]
Hence, arc PXA ≅ Arc PYB
Therefore, if two chords of a circle are equal, then their corresponding arcs are congruent.

Q.3. A, B and C are three points on a circle. Prove that the perpendicular bisectors of AB, BC and CA are concurrent.

According to the question,
Three non-collinear points A, B and C are on a circle.
To prove: Perpendicular bisectors of AB, BC and CA are concurrent.
Construction: Join AB, BC and CA.
Draw:
ST, perpendicular bisector of AB,
PM, perpendicular bisector of BC
And, QR perpendicular bisector of CA
As point A, B and C are not collinear, ST, PM and QR are not parallel and will intersect.
Proof:
O lies on ST, the ⊥ bisector of AB
OA = OB … (1)
Similarly, O lies on PM, the ⊥ bisector of BC
OB = OC … (2)
And, O lies on QR, the ⊥ bisector of CA
OC = OA … (3)
From (1), (2) and (3),
OA = OB = OC
Let OA = OB = OC = r
Draw circle, with centre O and radius r, passing through A, B and C.
Hence, O is the only point equidistance from A, B and C.
Therefore, the perpendicular bisectors of AB, BC and CA are concurrent.

Q.4. AB and AC are two equal chords of a circle. Prove that the bisector of the angle BAC passes through the centre of the circle.

According to the question,
We have,
AB and AC are two chords which are equal with centre O.
AM is the bisector of ∠BAC.
To prove: AM passes through O.
Construction: Join BC.
Let AM intersect BC at P.
Proof: In DBAP and DCAP
AB = AC [Given]
∠BAP = ∠CAP [Given]
And AP = BP [Common side]
△BAP ≅ △CAP [By SAS]
∠BPA = ∠CPA [CPCT]
We know that,
CP = PB
But, since ∠BPA and ∠CPA are linear pair angles,
We have,
∠BPA + ∠CPA = 180º
∠BPA = ∠CPA = 90º
Then,
AP is perpendicular bisector of the chord BC, which will pass through the centre O on being produced.
Therefore, AM passes through O.

Q.5. If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.

Consider AB and CD to be the chords of the circle with center O.
Let L be the midpoint of AB.
Let M be the midpoint of CD.
Let PQ be the line passing through these midpoints and the center of the circle.
Then, PQ is the diameter of the circle.
We know that,
Line joining center to the midpoint of a chord is always perpendicular to the chord.
Since M is the midpoint of CD,
We have, OM ⊥ CD
⇒ OMD = 90°
Similarly, L is the midpoint of AB,
OL ⊥ AB
⇒ OLA = 90°
But, we know, ∠OLA and ∠OMD are alternate angles.
So, AB ∥ CD.
Hence, proved.

Q.6. ABCD is such a quadrilateral that A is the centre of the circle passing through B, C and D. Prove that ∠CBD + ∠CDB = ½ ∠BAD

According to the question,
We have,
A quadrilateral ABCD such that A is the centre of the circle passing through B, C and D.
Construction:
Join CA and BD.
We know that,
In a circle, angle subtended by an arc at the center is twice the angle subtended by it at any other point in the remaining part of the circle
So,
The arc DC subtends ∠DAC at the center and ∠CAB at point B in the remaining part of the circle,
We get,
∠DAC = 2∠CBD …(1)
Similarly,
The arc BC subtends ∠CAB at the center and ∠CDB at point D in the remaining part of the circle,
We get,
∠CAB = 2∠CDB …(2)
From equations (1) and (2),
We have:
DAC + ∠CAB = 2∠CDB + 2∠CBD
⇒ ∠BAD = 2(∠CDB + ∠CBD)
⇒ (∠CDB + ∠CBD) = ½ (∠BAD).

Q.7. O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.

According to the question,
We have,
O is the circumcenter of the triangle ABC and D is the midpoint of BC.

To prove: ∠BOD = ∠A
Construction: Join OB and OC.
In ΔOBD and ΔCD:
OD = OD (common)
DB = DC (D is the midpoint of BC)
OB = OC (radius of the circle)
By SSS congruence rule,
We get,
ΔOBD ≅ ΔOCD.
∠BOD = ∠COD (By CPCT)
Let ∠BOD = ∠COD = x
We know that,
Angle subtended by an arc at the center of the circle is twice the angle subtended by it at any other point in the remaining part of the circle.
So, we have,
2∠BAC = ∠BOC
⇒ 2∠BAC = ∠BOD + ∠DOC
⇒ 2∠BAC = x + x
⇒ 2∠BAC = 2x
⇒ ∠BAC = x
⇒ ∠BAC = ∠BOD
Hence, proved.

Q.8. On a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite sides. Prove that ∠BAC = ∠BDC.

According to the question,
We have,
ACB and ADB are two right triangles.
To Prove: ∠BAC = ∠BDC
We know that,
ACB and ADB are right angled triangles,
Then,
∠C + ∠D = 90° + 90° ∠C + ∠D = 180°
Therefore ADBC is a cyclic quadrilateral as sum of opposite angles of a cyclic quadrilateral = 180°
We also have,
∠BAC and ∠BDC lie in the same segment BC and angles in the same segment of a circle are equal.
∴ ∠BAC = ∠BDC.
Hence Proved.

Q.9. Two chords AB and AC of a circle subtends angles equal to 90º and 150º, respectively at the centre. Find ∠BAC, if AB and AC lie on the opposite sides of the centre.

According to the question,
We have,
In ΔAOB,
OA = OB (radius of the circle)
Since angle opposite to equal sides are equal, we get,
∠OBA = ∠OAB
We know that,
According to angle sum property, sum of all angles of a triangle = 180°
Using the angle sum property in ΔAOB, we get,
∠OAB + ∠AOB +∠OBA = 180°
⇒ ∠OAB + 90° + ∠OAB = 180°
⇒ 2∠OAB = 180° – 90°
⇒ 2∠OAB = 90°
⇒ ∠OAB = 45°
Now, in ΔAOC,
OA = OC (radius of the circle)
Since, angle opposite to equal sides are equal
∴ ∠OCA = ∠OAC
Using the angle sum property in ΔAOB, sum of all angles of the triangle is 180°, we have:
∠OAC + ∠AOC +∠OCA = 180°
⇒ ∠OAC +150° + ∠OAC = 180°
⇒ 2∠OAC = 180° – 150°
⇒ 2∠OAC = 30°
⇒ ∠OAC = 15°
Now, ∠BAC = ∠OAB + ∠OAC
= 45° + 15°
= 60°
∴ ∠BAC = 60°.

Q.10. If BM and CN are the perpendiculars drawn on the sides AC and AB of the triangle ABC, prove that the points B, C, M and N are concyclic.

According to the question,
BM and CN are the perpendiculars drawn on the sides AC and AB of the triangle ABC.
So, we have,
∠BMC = ∠BNC = 90º
We know that,
If a line segment joining two points subtends equal angles on the same side of the line containing the segment, then the four points are concyclic.
Considering the question,
Since BC joins the two points, B and C, subtending equal angles, ∠BMC and ∠BNC, at M and N on the same side BC containing the segment, then B, C, M and N are concyclic.
Hence, we get that,
B, C, M and N are concyclic.

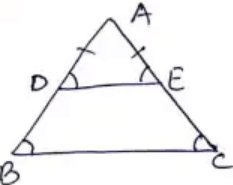
Q.11. If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral so formed is cyclic.

ABC is isosceles triangle.

DE ∥ BC

∴ ∠ADE = ∠ABC = ∠AED ⟶ (1)

∠AED = ∠ACB ⟶ (2)

∠ADE + ∠BDE = 180°  (straight line)

∠ACB + ∠BDE = 180° (∵∠AED = ∠ACB) ⟶ (3)

∠AED + ∠DEC = 180°  (straight line)

∠ABC + ∠DEC = 180°(∵ ∠ABC = ∠AED) ⟶ (4)

from (3) & (4),

Sum of opposite angles are 180°, which is the property of cyclic quadrilateral.

Q.12. If a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are also equal.

Let ABCD be a cyclic quadrilateral and AD = BC
AC and BD are diagonals of cyclic quadrilateral.
In △AOD and △BOC
⇒  ∠OAD = ∠OBC [ Same segment subtends equal angle to the circle ]
⇒  AD = BC [ Given ]
⇒  ∠ODA = ∠OCB [ Same segment subtends equal angle to the circle ]
∴  △AOD ≅ △BOC [ By ASA congruence rule ]
Adding △DOC on both sides, we get
⇒  △AOD + △DOC ≅ △BOC + △DOC
⇒  △ADC ≅ △BCD
⇒  AC = BD [ By CPCT ]

Hence, we have proved that, a pair of opposite sides of a cyclic quadrilateral are equal prove that its diagonals are also equal

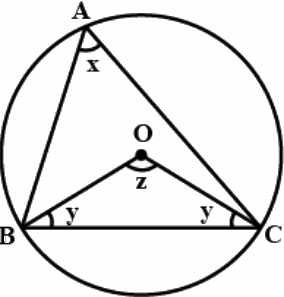
Q.13. The circumcentre of the triangle ABC is O. Prove that ∠OBC + ∠BAC = 90º.

O is circumcentre of ΔABC, join OB and OC. We know that
∴ ∠BOC = 2∠BAC
z = 2x
In ΔOBC
∠OBC + ∠OCB + ∠BOC = 180°
y + z + y = 180°
2y + z = 180°
2y + 2x = 180° 

2(x + y) = 180°
x + y = 90°
∠BAC + ∠OBC = 90°

or ∠OBC + ∠BAC = 90°

Q.14. A chord of a circle is equal to its radius. Find the angle subtended by this chord at a point in major segment.

Given- PQ is the chord of a circle with centre O and  PQ=OP=OQ.PQ subtends ∠POQ &  ∠PRQ at the centre and at the cicumference.
To find out- ∠PRQ = ?
Solution- PQ = OP = OQ.
∴ ΔPOQ is an equilateral one. So ∠POQ = 60°. i.e ∠PRQ = (1/2)∠POQ = (1/2) × 60° = 30°. (The angle subtended by a chord at the centre of a circle is double of that at the cicumference.)

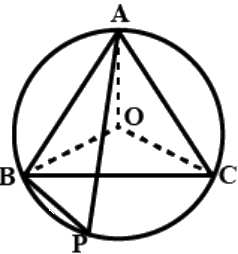
Q.15. In Fig.10.13, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.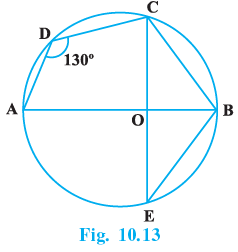

In △BCO and △BEO
⇒ BC = BE [Given]
⇒ ∠BCO = ∠BEO [Base angles of equal sides are also equal]
⇒ BO = BO [ Common side ]
∴ △BCO ≅ △BEO [By SAS congruence rule]
⇒ ∠CBO = ∠OBE [ C.P.C.T. ]
Quadrilateral ABCD is a cyclic quadrilateral since, its points lies on a circle.
⇒ ∠ADC + ∠CBA = 180°
[ Sum of opposite angles of a cyclic quadrilateral is supplementary ]
⇒ 130° + ∠CBA = 180°
⇒ ∠CBA = 50°
i.e. ∠CBO = 50°
∴ ∠OBE = 50°
⇒ ∠CBE = 50° + 50° = 100°.

Q.16. In Fig.10.14, ∠ACB = 40º. Find ∠OAB.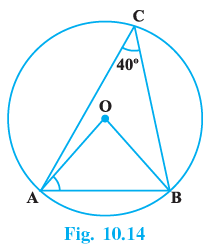

In ΔOAB, we have
OA = OB ...(radii of the same circle).
∴ ΔOAB is isosceles.
∴ ∠OAB = ∠OBA ⇒ ∠OAB + ∠OBA = 2∠OAB
So, ∠AOB + ∠OAB + ∠OBA = ∠AOB + 2∠OAB = 180° ....(angle sum property of triangles).

∴ ∠OAB= (1/2) (180° − ∠AOB) ...(i)
Now ∠AOB = 2∠ACB = 2 × 40° = 80° ...(The angle subtended by a chord of a circle at the centre is double of that at the cicumference)
From (i), we have
∠OAB = (1/2) (180° − 80°) = 50°

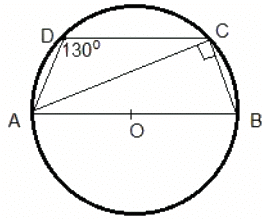
Q.17. A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.

Given, ABCD is a quadrilateral inscribed in a circle.
Also, ∠ADC = 130°.
We have to find: ∠BAC.
Now join AD.
Then, ∠ADC + ∠ABC = 180°...(The sum of the opposite angles of a cyclic quadrilateral = 180°)
i.e. ∠ABC = 180° −∠ADC = 180° −130° = 50°.
So, in ΔABC, we have, ∠BAC = 180° −(∠ACB + ∠ABC) ...(Since AB is the diameter, the angle subtended by the diameter of a circle at the circumference = 90°
i.e. ∠BAC = 90°)
=180° − (50° + 90°) = 40°.
Therefore, option (c) is correct.

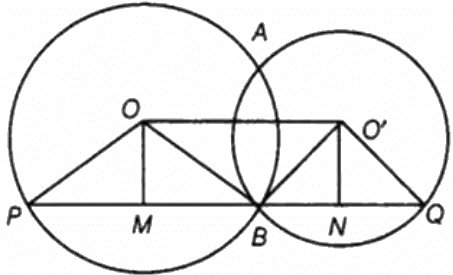
Q.18. Two circles with centres O and O′ intersect at two points A and B. A line PQ is drawn parallel to OO′ through A(or B) intersecting the circles at P and Q. Prove that PQ = 2 OO′.

Firstly draw two circles with center O and O’ such that they intersect at A and B.

Draw a line PQ parallel to OO’.
In the circle with center O, we have:
OP and OB are the radii of the circle. PB is the chord with OM as its perpendicular bisector.
i.e. BM = MP ...(1)
In the circle with center O’, we have:
O’B and O’Q are the radii of the circle. BQ is the chord with O’N as its perpendicular bisector.
i.e. BN = NQ...(1)BM = MP ...(1)
From (1) and (2), we have:
BM + BN = MP + NQ
⇒ (BM + BN) + (BM + BN) = (BM + BN) + (MP + NQ)
⇒ 2(BM + BN) = (BM + BN)+(MP + NQ)
⇒ 2(OO’) = (BM + MP)+(BN + NQ)
⇒ 2(OO’) = BP + BQ
⇒ 2OO’ = PQ
Hence, proved.

Q.19. In Fig.10.15, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED.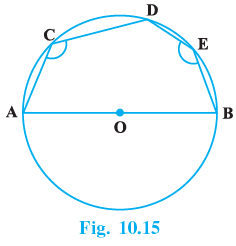

Join AE.
ACDE is a cyclic quadrilateral since all four points lies on circle.
⇒ ∠ACD+∠AED=180° [Sum of opposite angles of a cyclic quadrilateral is supplementary]
AB is a diameter of a circle.
⇒ ∠AEB = 90°  [Angle in a semi-circle] ...(2)
Adding ( 1 ) and ( 2 ) we get,
⇒ ∠ACD + ∠AED + ∠AEB = 180° + 90°
⇒ ∠ACD + ∠BED = 270°.

Q.20. In Fig. 10.16, ∠OAB = 30º and ∠OCB = 57º. Find ∠BOC and ∠AOC.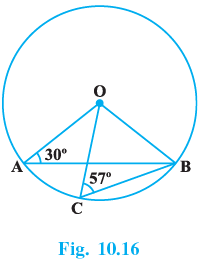

⇒ ∠OAB = 30° and ∠OCB = 57°.
In △AOB,
⇒ AO = OB [Radius of a circle]
⇒ ∠OBA = ∠BAO = 30° [Angles opposite to equal sides are equal]
In △AOB,

⇒ ∠AOB + ∠OBA + ∠BAO = 180°.
∴  ∠AOB + 30° + 30° = 180°
∴ ∠AOB = 180°−30° −30°
∴ ∠AOB = 120° (1)
Now, in △OCB,
⇒ OC = OB [Radius of a circle]
⇒ ∠OBC = ∠OCB = 57°.  [ Angles opposite to equal sides are equal ]

In △OCB,
⇒ ∠BOC + ∠OCB + ∠OBC = 180°.
⇒ ∠BOC + 57° + 57° = 180°
⇒ ∠BOC=180° − 114°
∴ ∠BOC = 66° ...( 2 )
⇒ ∠AOB = 120° [From (1)]
⇒ ∠AOC + ∠COB = 120°.
⇒ ∠AOC + 66° = 120°
⇒ ∠AOC = 120° − 66°
∴ ∠AOC = 54°

Q.1. If two equal chords of a circle intersect, prove that the parts of one chord are separately equal to the parts of the other chord.

According to the question, AB and CD are two equal chords of a circle with centre O, intersect each other at M.
To prove:
(i) MB = MC and
(ii) AM = MD
Proof:
AB is a chord and OE ⊥ to AB from the centre O,
Since, perpendicular from the centre to a chord bisect the chord
We get,
AE = ½ AB
Similarly,
FD = ½ CD
It is given that,
AB = CD ⇒ ½ AB = ½ CD
So, AE = FD … (1)
Since equal chords are equidistance from the centre,
And AB = CD
So, OE = OF
Now, as proved, in right triangles MOE and MOF,
hyp. OE = hyp. OF [Common side]
OM = OM
ΔMOE ≅ ΔMOF
ME = MF … (2)
Subtracting equations (2) from (1), we get
AE – ME = FD – MF
⇒ AM = MD [Proved part (ii)]
Again, AB = CD [Given]
And AM = MD [Proved]
AB – AM = CD – MD [Equals subtracted from equal]
Hence, MB = MC [Proved part (i)]

Q.2. If non-parallel sides of a trapezium are equal, prove that it is cyclic.

According to the question,
We have,
ABCD is a trapezium in which AD||BC
Non-parallel sides AB and DC of the trapezium ABCD are equal i.e.,
AB = DC.
To prove: Trapezium ABCD is cyclic.
Construction: Draw AM and DN such that they are perpendicular on BC.
Proof: In right triangles AMB and DNC,
∠AMB = ∠DNC = 90º
AB = DC [Given]
Since perpendicular distance between two parallel lines are same,
AM = DN
ΔAMB ≅ ΔDNC [By RHS congruence rule]
∠B = ∠C [CPCT]
And ∠1 = ∠2
∠BAD = ∠1+ 90
= ∠2 + 90
= ∠CDA
Now, in quadrilateral ABCD
∠B +∠C +∠CDA+∠BAD = 360
∠B +∠B +∠CDA+∠CDA = 360
2(∠B +∠CDA) = 360
∠B +∠CDA =180
We know that,
If any pair of opposite angles of a quadrilateral is 180o, then the quadrilateral is cyclic.
Hence, the trapezium ABCD is cyclic.

Q.3. If P, Q and R are the mid-points of the sides BC, CA and AB of a triangle and AD is the perpendicular from A on BC, prove that P, Q, R and D are concyclic.

To prove: R, D, P and Q are concyclic.
Construction: Join RD, QD, PR and PQ.
RP joins the mid-point of AB, i.e., R, and the mid-point of BC, i.e., P.
Using midpoint theorem,
RP||AC
Similarly,
PQ||AB.
So, we get,
ARPQ is a parallelogram.
So, ∠RAQ = ∠RPQ [Opposite angles of a ||gm]…(1)
ABD is a right angled triangle and DR is a median,
RA = DR and ∠1 = ∠2 …(2)
Similarly ∠3 = ∠4 …(3)
Adding equations (2) and (3),
We get,
∠1+ ∠3 = ∠2 +∠4
⇒ ∠RDQ = ∠RAQ ∠RPQ [Proved above]
Since ∠D and ∠P are subtended by RQ on the same side of it, we get the points R, D, P and Q concyclic.
Hence, R, D, P and Q are concyclic.

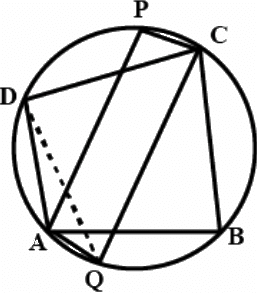
Q.4. ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.

According to the question,
ABCD is a parallelogram.
A circle through A, B is so drawn that it intersects AD at P and BC at Q.
To prove: P, Q, C and D are concyclic.
Construction: Join PQ.
Extend side AP of the cyclic quadrilateral APQB to D.
External angle, ∠1 = interior opposite angle, ∠B
Since, BA||CD and BC cuts them
∠B +∠C = 180º
Since, Sum of interior angles on the same side of the transversal = 180º
Or ∠1+∠C = 180º
So, PDCQ is cyclic quadrilateral.
Hence, the points P, Q, C and D are concyclic.

Q.5. Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.

According to the question,
Triangle ABC and l is perpendicular bisector of BC.
To prove: Angles bisector of ∠A and perpendicular bisector of BC intersect on the circumcircle of ΔABC.
Proof: Let the angle bisector of ∠A intersect circumcircle of ΔABC at D.
Construction: Join BP and CP.
Since, angles in the same segment are equal
We have, ∠BAP = ∠BCP
We know that,
AP is bisector of ∠A.
Then,
∠BAP = ∠BCP = ½ ∠A …(1)
Similarly,
We have,
∠PAC = ∠PBC = ½ ∠A …(2)
From equations (1) and (2),
We have
∠BCP = ∠PBC
We know that,
If the angles subtended by two Chords of a circle at the centre are equal, the chords are equal.
So,
BP = CP
Here, P is on perpendicular bisector of BC.
Hence, angle bisector of ∠A and perpendicular bisector of BC intersect on the circumcircle of ΔABC.

Q.6. If two chords AB and CD of a circle AY DZBW CX intersect at right angles (see Fig.10.18), prove that arc CXA + arc DZB = arc AY D + arc BW C = semicircle.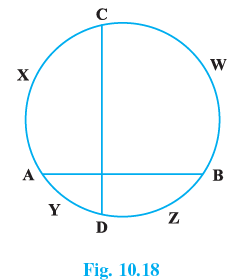

A chord divides the circumference of a circle in a way that their mean is the circumference of the semicircle.
The difference in the length of arcs is inversely proportional to the length of the chord.
And for mutually perpendicular chords the difference in the length of arcs cut by chords are the same.
So, by using the above statement we can say that,
BWC − DZB = CXA − AYD
CXA + DZB = AYD + BWC …(i)
And they all sum up to give the circumference of the circle.
CWB + BZD + CXA + DYA = 2πr
2(BWC + AYD) = 2πr or 2(CXA + DZB) = 2πr by using (i)
BWC + AYD = πr or CXA + DZB = 2πr
πr is nothing but the length of the semicircle. Hence proved.

Q.7. If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.

Here, △ABC is an equilateral triangle inscribed in a circle with centre O.
⇒ AB = AC = BC  [∵△ABC is equilateral]
∠AOB = ∠AOC = ∠BOC [equal chords subtend equal angles at centre]
⇒ ∠AOB = ∠AOC ...i)
Now, ∠AOB and ∠APB are angles subtended by an arc AB at centre and at remaining part of the circle by same arc.
Therefore, ∠APB = (∠AOB/2) ...(ii)
Similarly,   ∠APC =(∠AOC/2) ...(iii)
Using (i), (ii) and (iii), we have
∠APB = ∠APC
Hence, PA is angle bisector of ∠BPC.

Q.8. In Fig. 10.19, AB and CD are two chords of a circle intersecting each other at point E. Prove that ∠AEC = (1/2) (Angle subtended by arc CXA at centre+ angle subtended by arc DYB at the centre).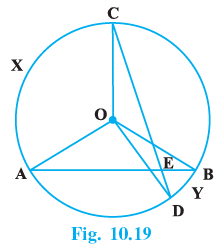

AB and CD are two chords of a circle intersecting each other at point E.
We have to prove that ∠AEC= (1/2) (Angles subtended by an arc CXA at the centre + angle subtended by arc DYB at the centre.)
Join AC.BC and BD
Since, the angles subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle. now arc CXA subtends ∠AOC at the centre and ∠ABC at the remaining pan of the circle, so
∠AOC = 2∠ABC ...(1)
Similarly, ∠BOD = 2∠BCD ...(2)
Now, adding (1) and (2), we get
∠AOC + ∠BOD = 2(∠ABC + ∠BCD) ...(3)
Since exterior angle of a triangle is equal to the sum of interior opposite angles,
so in ΔCEB, we have
∠AEC + ∠ABC + ∠BCD ...(4)
From (3) and (4), we get
∠AOC + ∠BOD = 2∠AEC
or ∠AEC= 1/2(∠AOC + ∠BOD)
Hence, ∠AEC = (1/2) (angles subtended by an arc CXA at the centre + angle substended by an arc DYB at the centre).

Q.9. If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.

ABCD is a cyclic quadrilateral. The bisectors of its opposite angles A and C intersect the circle circumscribing at the points P and Q respectively.

⇒  ∠A+∠C=180° [Opposite angles of a cyclic quadrilateral are supplementary]

⇒ (1/2)∠A +  (1/2) ∠C = 90°
⇒ ∠PAB + ∠BCQ = 90°

But ∠BCQ = ∠BAQ [Angles in the segment of a circle are equal]
∴  ∠PAB+∠BAQ = 90°
⇒  ∠PAQ=90°
⇒  But ∠PAQ is in semicircle.
∴  PQ is diameter of the circle.

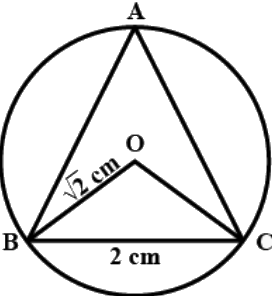
Q.10. A circle has radius √2 cm. It is divided into two segments by a chord of length 2 cm. Prove that the angle subtended by the chord at a point in major segment is 45º.

∠BAC lies in the major segment.
Refer image,
We have to prove that ∠BAC = 45°
Join OB and OC

⇒ BC² = OB² + OC²
In ΔBOC, we have
BC² = OB² + OC²
∴ ∠BOC = 90° [By converse of Pythagoras theorem]
Now, BC subtends ∠BOC at the centre O  
∠BAC at the remaining part of the circle.

Hence proved.

Q.11. Two equal chords AB and CD of a circle when produced intersect at a point P. Prove that PB = PD.

Given two equal chords AB and CD of a circle interesting at a point P.

To prove that PB = PD.
Construction : Join OP, draw OL ⊥ AB and OM ⊥ CD.
Proof: We have, AB = CD
OL = OM [equal chords are equidistant from the centre]
In ΔOLP and ΔOMP, we have
OL = OM [proved above]
∠OLP = ∠OMP [each 90°]
And, OP = OP [common side]
∴ ΔOLP ≅ ΔOMP [by RHS congruence rule]
LP = MP [by CPCT] ...(i)
Now, AB = CD
⇒ (1/2)(AB) = (1/2)(CD) [dividing both sides by 2]
⇒ BL = DM...(ii)
[perpendicular draw from centre to the circle bisects the chord i.e., AL = LB and CM = MD]
On subtracting Eq. (ii) from Eq. (i), we get
LP - BL = MP - DM
⇒ PB = PD. hence proved.

Q.12. AB and AC are two chords of a circle of radius r such that AB = 2AC. If p and q are the distances of AB and AC from the centre, prove that 4q² = p² + 3r².

Consider the diagram shown below.
Given:
AB and AC are two chords of a circle with center O. Such that AB = 2AC
p and q are ⊥ distances of AB and AC from center O i.e., OM = p and ON = q
r is the radius of the circle
To prove that:
4q² = p² + 3r²

Proof:
Join OA.
OM and ON are ⊥ distances of AB and AC from center O.
Here,
AN = (AC/2) (perpendicular from center to chord intersect at mid-point of the chord)
AM = (AB/2) (perpendicular from center to chord intersect at mid-point of the chord)
In right angled ΔOMA,
OM² + AM² = OA²
p² + AM² = r²
AM² = r² − p² …(1)
In right angled ΔONA,
ON² + AN² = OA²
q² + AN² = r²
AN² = r²− q² ...(2)
Since,

From equations (1) and (2), we have
r² − p² = AM²
r² − p² = 4AN²
r² - p² = 4[r² - q²]
4q² = p² + 3r²
LHS = RHS
Hence, proved.

Q.13. In Fig. 10.20,O is the centre of the circle, ∠BCO = 30°. Find x and y.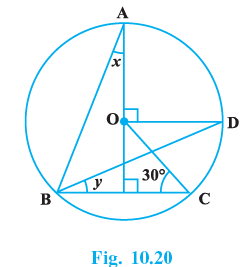

Given
BA, BD & BC are the chords of the circle with centre O.
AE ⊥ BC & OD ⊥ AE.
∠OCE = 30°.
To find out−
∠BAE = x = ? And ∠DBC = y = ?
Solution−
We join AD & DC.
∠ABD = (1/2) ∠AOD = (1/2) x 90° = 45°.
(∵ The angle at the centre of a circle subtended by a chord is double of that at the circumference.).
∴ In ΔOEC we have ∠COE = 180° −(∠OEC + ∠OCE)=180° −(90° + 30°)= 60°. (angle sum property of triangles)
∴ ∠DOC = ∠DOE − ∠COE = 90° − 60° = 30°.
Now ∠DBC = y = (1/2) ∠DOC = (1/2) × 30° = 15°.
(∵ The angle at the centre of a circle subtended by a chord is double of that at the circumference.).
Again ∠ABE = y + 45° = 45° + 15° = 60°.
∴ In ΔABE we have ∠BAE = x = 180° − (∠ABE + ∠AEB) = 180° − (60°  + 90°) = 30°. (angle sum property of triangles)
So x = 30° & y = 15°.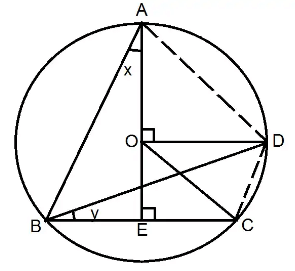
 

Q.14. In Fig. 10.21, O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.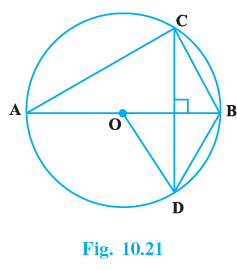

Given- BD is a chord of the circle with centre O, is equal to the radius OD of the circle.  
The diameter AOB ⊥ DC.
AC and BC are two other chords.

To find out-

∠CAB = ?

Solution:
In △ODB, we have
OD = OB ...(radii of the same circle) = BD.
∴ ΔODB is equilateral.
i.e all the angles = 60°
∴ ∠OBD = 60°
∴ ∠ABD + ∠BDC + 90° = 180° ...(angle sumd property of triangles).

⇒ ∠BDC = 180°−90°−60° = 30°
Now the chord BC subtends ∠BACand ∠BDC at the cicumference.
∴ ∠BAC = ∠BDC = 30°
The angles subtended by a chord of a circle at the circumference are equal.