NCERT Exemplar Solutions: Introduction to Euclid's Geometry | Mathematics (Maths) Class 9 PDF Download
Exercise 5.1
Q.1. The three steps from solids to points are:
(a) Solids - surfaces - lines - points
(b) Solids - lines - surfaces - points
(c) Lines - points - surfaces - solids
(d) Lines - surfaces - points - solids
Correct Answer is Option (a)
We know that
A solid has size, shape and position.
The boundaries are called surfaces
The boundaries of the surfaces are straight lines or curves.
The points are the ends of these lines
Therefore, the three steps are solids - surfaces - lines - points.
Q.2. The number of dimensions, a solid has :
(a) 1
(b) 2
(c) 3
(d) 0
Correct Answer is Option (c)
I step - Let us describe the dimensions in a solid
The measurement in a particular direction is the dimension.
A solid has length, breadth and height.
II step - Determine the number of dimensions in the solid
Number of dimensions in a solid is 3
Therefore, a solid has 3 number of dimensions
Q.3. The number of dimensions, a surface has :
(a) 1
(b) 2
(c) 3
(d) 0
Correct Answer is Option (b)
We know that
A continuous set of points which has length and breadth but no thickness is called a surface.
So it has two dimensions
Therefore, a surface has 2 dimensions.
Q.4. The number of dimension, a point has :
(a) 0
(b) 1
(c) 2
(d) 3
Correct Answer is Option (a)
We know that
A point marks a place and has no length, breadth and thickness
A point is devoid of three fundamental dimensions
Therefore, a point has 0 dimension.
Q.5. Euclid divided his famous treatise “The Elements” into :
(a) 13 chapters
(b) 12 chapters
(c) 11 chapters
(d) 9 chapters
Correct Answer is Option (a)
We know that
Euclid’s Treatise “The Elements” is written in 13 chapters
It mainly deals with Solid figures, Plane Geometry, Fundamental arithmetic and few typical problems
Therefore, Eulcid divided his famous treatise into 13 chapters.
Q.6. The total number of propositions in the Elements are :
(a) 465
(b) 460
(c) 13
(d) 55
Correct Answer is Option (a)
We know that
Theorems or propositions are statements which can be proved
Euclid deduced 465 propositions in a logical chain making use of his definitions, postulates, axioms and theorems.
Therefore, the total number of propositions is 465.
Q.7. Boundaries of solids are :
(a) surfaces
(b) curves
(c) lines
(d) points
Correct Answer is Option (a)
We know that
Boundaries of solids are known as surfaces whereas boundaries of surfaces are known as curves.
Therefore, the boundaries of solids are surfaces.
Q.8. Boundaries of surfaces are :
(a) surfaces
(b) curves
(c) lines
(d) points
Correct Answer is Option (b)
We know that
Boundaries of surfaces are known as curves whereas boundaries of solids are known as surfaces.
Therefore, the boundaries of surfaces are curves.
Q.9. In Indus Valley Civilisation (about 3000 B.C.), the bricks used for construction work were having dimensions in the ratio
(a) 1 : 3 : 4
(b) 4 : 2 : 1
(c) 4 : 4 : 1
(d) 4 : 3 : 2
Correct Answer is Option (b)
We know that
The bricks used for construction in the Indus Valley Civilisation are in the ratio
Length: Breadth: Thickness = 4: 2: 1
Therefore, the dimensions of the bricks are in the ratio 4: 2: 1.
Q.10. A pyramid is a solid figure, the base of which is
(a) only a triangle
(b) only a square
(c) only a rectangle
(d) any polygon
Correct Answer is Option (d)
We know that
In mathematics, a pyramid is a 3D figure built with a base of a polygon and triangular faces all connected together.
A pyramid is a 3D polyhedron with the base of a polygon along with three or more triangle-shaped faces that meet at a point above the base.
The triangular sides are called faces and the point above the base is called the apex.
A pyramid is made by connecting the base to the apex.
A pyramid is a solid figure, the base of which is a square, triangle or some other polygonTherefore, a pyramid is a solid figure, the base of which is any polygon.
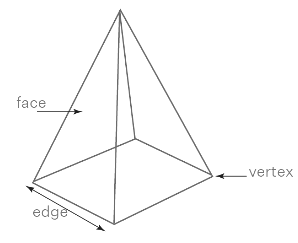
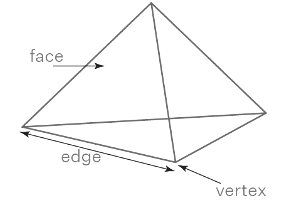
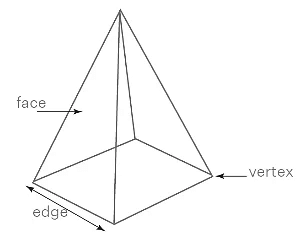
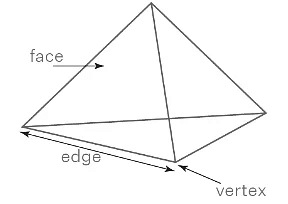
Q.11. The side faces of a pyramid are :
(a) Triangles
(b) Squares
(c) Polygons
(d) Trapeziums
Correct Answer is Option (a)
Let us consider the pyramids mentioned belowFrom these figures we get to know that the side faces are triangles.
Therefore, the side faces of a pyramid are triangles.
Q.12. It is known that if x + y = 10 then x + y + z = 10 + z. The Euclid’s axiom that illustrates this statement is :
(a) First Axiom
(b) Second Axiom
(c) Third Axiom
(d) Fourth Axiom
Correct Answer is Option (b)
The equation given is
x + y = 10
By adding z on both sides
x + y + z = 10 + z
Here z is added to quantities which are equal
From the Euclid’s second axiom “If equals be added to the equals, the wholes are equal”
Euclid’s second axiom illustrates this statement.
Therefore, the Euclid’s second axiom illustrates this statement.
Q.13. In ancient India, the shapes of altars used for house hold rituals were :
(a) Squares and circles
(b) Triangles and rectangles
(c) Trapeziums and pyramids
(d) Rectangles and squares
Correct Answer is Option (a)
We know that
Shapes of altars used for household rituals were squares and circles
Therefore, the shapes of altars were squares and circles.
Q.14. The number of interwoven isosceles triangles in Sriyantra (in the Atharvaveda) is:
(a) Seven
(b) Eight
(c) Nine
(d) Eleven
Correct Answer is Option (c)
We know that
Sriyantra has nine interwoven isosceles triangles.Therefore, the number of interwoven isosceles triangles is nine.
Q.15. Greek’s emphasised on :
(a) Inductive reasoning
(b) Deductive reasoning
(c) Both A and B
(d) Practical use of geometry
Correct Answer is Option (b)
We know that
Egyptians developed a number of geometric techniques and rules for calculating simple areas and doing simple constructions.
Babylonians and Egyptians used geometry mostly for practical purposes and did very little to develop it as a systematic science.
The Greeks were interested in establishing the truth of the statements they discovered using deductive reasoning.
A Greek mathematician, Thales is credited with giving the first known proof.
Therefore, Greek’s emphasised on deductive reasoning.
Q.16. In Ancient India, Altars with combination of shapes like rectangles, triangles and trapeziums were used for :
(a) Public worship
(b) Household rituals
(c) Both A and B
(d) None of A, B, C
Correct Answer is Option (a)
We know that
An altar is a structure with an upper surface for the presentation of religious offerings, for sacrifices, or for other ritualistic purposes.
The geometry of Vedic period originated with the altars construction and fireplaces which are used for performing the rites.
For household rituals, circular and square altars were used whereas altars with shapes that are combinations of triangles, trapeziums and rectangles are used for public worship.
Therefore, the altars with combinations of shapes like rectangles, triangles and trapeziums were used for public worship.
Q.17. Euclid belongs to the country :
(a) Babylonia
(b) Egypt
(c) Greece
(d) India
Correct Answer is Option (c)
We know that
Euclid belongs to Greece.
Therefore, Euclid belongs to the country Greece.
Q.18. Thales belongs to the country:
(a) Babylonia
(b) Egypt
(c) Greece
(d) Rome
Correct Answer is Option (c)
We know that
Thales belongs to Greece.
Therefore, Thales belongs to the country Greece.
Q.19. Pythagoras was a student of :
(a) Thales
(b) Euclid
(c) Both A and B
(d) Archimedes
Correct Answer is Option (a)
We know that
Pythagoras was a student of Thales.
Therefore, Pythagoras was a student of Thales.
Q.20. Which of the following needs a proof ?
(a) Theorem
(b) Axiom
(c) Definition
(d) Postulate
Correct Answer is Option (a)
We know that
Axiom, definition and postulate are self evident and no proof is required.
A proposition which requires a proof to establish the truth is a theorem.
Therefore, the theorem needs a proof.
Q.21. Euclid stated that all right angles are equal to each other in the form of
(a) an axiom
(b) a definition
(c) a postulate
(d) a proof
Correct Answer is Option (c)
We know that
All right angles are equal to one another is Euclid’s fourth postulate.
Therefore, the statement is in the form of a postulate.
Q.22. ‘Lines are parallel if they do not intersect’ is stated in the form of
(a) an axiom
(b) a definition
(c) a postulate
(d) a proof
Correct Answer is Option (b)
We know that
A postulate or an axiom is a statement which is taken to be true without any proof.
An evidence which establishes a theorem or fact is a proof.
A statement of the exact meaning of a word is a definition.
Here
‘Lines are parallel if they do not intersect’ is the definition of parallel lines as it conveys the meaning of parallel or what is meant by two lines are parallel.
Therefore, the statement is in the form of a definition.
Exercise 5.2
Q.1. Euclidean geometry is valid only for curved surfaces. Is the given statement true or false? Justify your answer
We know that
Euclidean geometry is based on the postulates and axioms that are valid for plane surfaces.
Euclidean is not physical space whereas curved space needs physical space.
So it is not valid for curved surfaces.
Therefore, the statement is false.
Q.2. The boundaries of the solids are curves. Is the given statement true or false? Justify your answer
We know that
The boundaries of the solids are surfaces
The boundaries of surfaces are curves.
Therefore, the statement is false.
Q.3. The edges of a surface are curves. Is the given statement true or false? Justify your answer
We know that
Edges of a surface are known as lines
Therefore, the statement is false.
Q.4. The things which are double of the same thing are equal to one another. Is the given statement true or false? Justify your answer
From the Euclidean axiom
The things which are double of the same thing are equal to one another
For example -
If 2x = 2y then x = y
Therefore, the statement is true.
Q.5. If a quantity B is a part of another quantity A, then A can be written as the sum of B and some third quantity C. Is the given statement true or false? Justify your answer
Consider a quantity A having two parts B and C
When A coincide with B and C
From the fourth Euclidean Axiom
Things which coincide with one another are equal to one another
A = B + C
Therefore, the statement is true.
Q.6. The statements that are proved are called axioms. Is the given statement true or false? Justify your answer
We know that
Axioms are statements that are self-evident and are accepted without any proof.
A few statements need proof and verification experimentally in order to establish themselves.
This type of statement is known as theory
Therefore, the statement is false.
Q.7. “For every line l and for every point P not lying on a given line l, there exists a unique line m passing through P and parallel to l ” is known as Playfair’s axiom. Is the given statement true or false? Justify your answer
Consider the lines l is parallel to the line m through a point P outside the line l
Consider n as another line that pass through P
From P a line PQ is drawn to Q on l
Let PQ make angle c with l and alternate angle a with m
As l and m is parallel
∠c = ∠a …. (1)
Consider another line n parallel to l and pass through P
Angle alternate to c made by n with PQ is b
As l and n are parallel
∠c = ∠b …. (2)
From Euclid’s first axiom
∠a = ∠b
Either ∠a is a part of ∠b or ∠b is a part of ∠a
From Euclid’s fifth axiom
∠a = ∠b
Therefore, the statement is true.
Q.8. Two distinct intersecting lines cannot be parallel to the same line. Is the given statement true or false? Justify your answer
We know that
Intersecting lines cannot be parallel
Therefore, the statement is true.
Q.9. Attempts to prove Euclid’s fifth postulate using the other postulates and axioms led to the discovery of several other geometries. Is the given statement true or false? Justify your answer
Euclid’s fifth postulate is “If a straight line falling on two straight lines makes the interior angles on the same side of it, taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is taken together less than two right angles.”
Attempts to prove Euclid’s fifth postulate using the other postulates and axioms led to the discovery of several other geometries.
These are quite different from Euclidean geometry and are known as non-Euclidean geometry.
Therefore, the statement is true.
Exercise 5.3
Q.1. Two salesmen make equal sales during the month of August. In September, each salesman doubles his sales for the month of August. Compare their sales in September. Solve using Euclid’s axiom
Given, two salesmen make equal sales during the month of August.
In September, each salesman doubles his sales for the month of August.
We have to compare their sales in September.
Let the sale of one salesman in August be x.
Given, sales are equal.
So, sale of other salesman in August = x
In September, sale of first salesman = 2x
Sale of second salesman = 2x
Using Euclid’s axiom,
Things which are double of the same thing are equal to one another
Therefore, in September the sales are equal.
Q.2. It is known that x + y = 10 and that x = z. Show that z + y = 10. Solve using Euclid’s axiom
Given, x + y = 10 --------- (1)
Also, x = z ---------- (2)
We have to show that z + y = 10
Using Euclid’s second axiom,
If equals are added to the equals, the wholes are equal.
From (2),
x + y = z + y
From (1),
z + y = 10
Therefore, z + y = 10
Q.3. Look at the Fig. 5.3. Show that length AH > sum of lengths of AB + BC + CD. Solve using Euclid’s axiom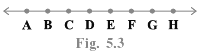
The figure represents the points A, B, C, D, E, F, G and H on the number line.
We have to show that the length AH > sum of lengths of AB + BC + CD
From the figure,
AH = AB + BC + CD + DE + EF + GH ----------- (1)
AB, BC, CD, DE, EF and GH are the parts of AH
Similarly, AB + BC + CD = AD ------------ (2)
So, AB, BC and CD are the parts of AD
Using Euclid’s axiom,
The whole is greater than the part.
From (1) and (2), we observe that
AD is a part of AH
Length of AH = length of AD + DE + EF + GH
Therefore, length AH > sum of lengths of AB + BC + CD
Q.4. In Fig.5.4, we have AB = BC, BX = BY. Show that AX = CY. Solve using Euclid’s axiom
The figure represents a triangle ABC.
The points X and Y lie on the sides AB and BC of the triangle ABC.
Given, AB = BC --------- (1)
Also, BX = BY ----------- (2)
We have to show that AX = CY
From the figure,
AB = AX + BX
So, AB - BX = AX ------------- (3)
Similarly,
BC = BY + CY
BC - BY = CY ----------- (4)
By using Euclid’s axiom,
If equals be subtracted from equals, the remainders are equal.
Using (1) and (2) in (3) and (4),
AB - BX = BC - BY
Therefore, AX = CY
Q.5. In Fig.5.5, we have X and Y are the mid-points of AC and BC and AX = CY. Show that AC = BC. Solve using Euclid’s axiom.
We have, X is the mid-point of AC.
∴
AX = CX = ½ AC
⇒ 2AX = 2CX = AC …(i)
and Y is the mid-point of BC.
∴
BY = CY = ½ BC
⇒ 2BY = 2CY = BC …(ii)
Also, given AX = CY …(iii)
⇒ 2AX = 2CY
[∵ Things which are double of the same
things are equal to one another]
⇒ AC = BC [From (i) and (ii)]
Q.6. In Fig.5.6, we have BX = 1/2 AB, BY = 1/2 BC and AB = BC. Show that BX = BY. Solve using Euclid’s axiom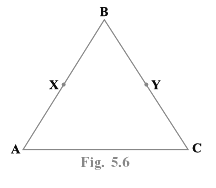
The figure represents a triangle ABC.
The points X and Y lie on the sides AB and BC.
Given, BX = AB/2 ------------ (1)
BY = BC/2 ------------ (2)
Also, AB = BC ----------- (3)
We have to show that BX = BY
From (1), AB = 2BX
This implies X is the midpoint of AB
From (2), BC = 2BY
This implies Y is the midpoint of BC
Using Euclid’s axiom,
Things which are double of the same thing are equal to one another.
From (3), 2BX = 2BY
Therefore, BX = BY
Q.7. In the Fig.5.7, we have ∠1 = ∠2, ∠2 = ∠3. Show that ∠1 = ∠3. Solve using Euclid’s axiom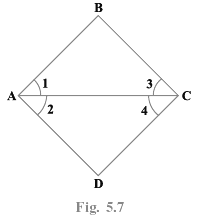
The figure represents a quadrilateral ABCD.
Given, ∠1 = ∠2 ------------- (1)
Also, ∠2 = ∠3 ------------ (2)
We have to show that ∠1 = ∠3.
From (1) and (2),
∠1 = ∠2 = ∠3
By using Euclid’s axiom,
The things which are equal to the same thing are equal to one another.
Therefore, ∠1 = ∠3
Q.8. In the Fig. 5.8, we have ∠1 = ∠3 and ∠2 = ∠4. Show that ∠A = ∠C. Solve using Euclid’s axiom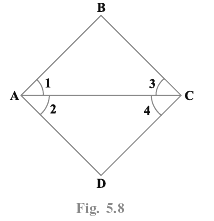
The figure represents a quadrilateral ABCD.
Given, ∠1 = ∠3 -------------- (1)
Also, ∠2 = ∠4 ---------------- (2)
We have to show that ∠A = ∠C.
On adding (1) and (2),
∠1 + ∠2 = ∠3 + ∠4
By using Euclid’s axiom,
If equals are added to the equals, the wholes are equal.
From the figure,
∠1 + ∠2 = ∠A
∠3 + ∠4 = ∠C
Therefore, ∠A = ∠C
Q.9. In the Fig. 5.9, we have ∠ABC = ∠ACB, ∠3 = ∠4. Show that ∠1 = ∠2. Solve using Euclid’s axiom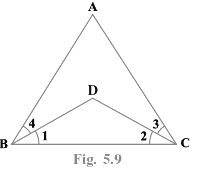
The figure represents two triangles ABC and BDC with common base BC.
Given, ∠ABC = ∠ACB -------- (1)
Also, ∠3 = ∠4 ------------ (2)
We have to show that ∠1 = ∠2
From the figure,
∠ABC = ∠1 + ∠4
∠1 = ∠ABC - ∠4 ------------- (3)
∠ACB = ∠3 + ∠2
∠2 = ∠ACB - ∠3 ------------ (4)
By using Euclid’s axiom,
If equals be subtracted from equals, the remainders are equal.
From (3) and (4),
∠ABC - ∠4 = ∠ACB - ∠3
Therefore, ∠1 = ∠2
Q.10. In the Fig. 5.10, we have AC = DC, CB = CE. Show that AB = DE. Solve using Euclid’s axiom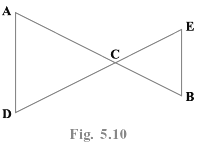
The figure represents two triangles ADC and CBE with common vertex C.
Given, AC = DC ----------- (1)
Also, CB = CE -------------- (2)
We have to show that AB = DE.
By using Euclid’s axiom,
If equals are added to the equals, the wholes are equal.
On adding (1) and (2),
AC + CB = DC + CE
From the figure,
AC + CB = AB ------------- (3)
Similarly, DC + EC = DE -------- (4)
From (3) and (4),
AB = DE
Therefore, it is proved that AB = DE
Q.11. In the Fig. 5.11, if OX = 1/2 XY, PX = 1/2 XZ and OX = PX, show that XY = XZ. Solve using Euclid’s axiom

The figure represents a triangle XYZ.
The points O and P lie on the sides XY and XZ.
Given, OX = XY/2 --------- (1)
PX = XZ/2 ---------- (2)
Also, OX = PX ---------- (3)
We have to show that XY = XZ.
From (1), XY = 2OX
This implies O is the midpoint of XY
So, XY = 2OX = 2OY ---------- (4)
From (2), XZ = 2PX
This implies P is the midpoint of XZ
So, XZ = 2PX = 2PZ ------------- (5)
According to Euclid’s axiom,
Things which are double of the same thing are equal to one another
Using (3) in (4) and (5), we get
2OX = 2PX
Therefore, XY = XZ
Q.12. In the Fig.5.12 :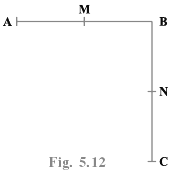 (i) AB = BC, M is the mid-point of AB and N is the mid- point of BC. Show that AM = NC. Solve using Euclid’s axiom
(i) AB = BC, M is the mid-point of AB and N is the mid- point of BC. Show that AM = NC. Solve using Euclid’s axiom
The figure represents two line segments AB and BC.
Given, AB = BC ------------- (1)
M is the midpoint of AB
N is the midpoint of BC
We have to show that AM = NC
Since M is the midpoint of AB we get
AB = 2AM = 2BM
AM = BM = AB/2------------ (2)
Since N is the midpoint of BC, we get
BC = 2BN = 2NC
BC = BN = NC/2 ------------ (3)
By using Euclid’s axiom,
Things which are halves of the same thing are equal to one another.
Multiplying (1) by 1/2 on both sides, we get
AB/2 = BC/2
From (2) and (3),
BM = BN
AM = NC
Therefore, it is proved that AM = NC
(ii) BM = BN, M is the mid-point of AB and N is the mid-point of BC. Show that AB = BC. Solve using Euclid’s axiom
The figure represents two line segments AB and BC.
Given, BM = BN --------- (1)
M is the midpoint of AB
N is the midpoint of BC
We have to show that AB = BC
Since M is the midpoint of AB we get
AB = 2AM = 2BM ----------- (2)
Since N is the midpoint of BC, we get
BC = 2BN = 2NC ----------- (3)
By using Euclid’s axiom,
Things which are double of the same thing are equal to one another.
Using (1) in (2) and (3),
2BM = 2BN
AB = BC
Therefore, AB = BC
Exercise 5.4
Q.1. Read the following statement: An equilateral triangle is a polygon made up of three line segments out of which two line segments are equal to the third one and all its angles are 60° each. Define the terms used in this definition which you feel necessary. Are there any undefined terms in this? Can you justify that all sides and all angles are equal in a equilateral triangle.
Given, the statement is “An equilateral triangle is a polygon made up of three line segments out of which two line segments are equal to the third one and all its angles are 60° each”.
We have to define the terms used in the definition.
We have to find the undefined terms
We have to justify that all the sides and all angles are equal in an equilateral triangle.
The terms used in the definition,
Polygon : a plane figure with at least three straight sides and angles, and typically five or more.
Line segment : a piece or part of a line having two endpoints
Angle : the space measured in degree, between two intersecting lines or surfaces at or close to the point where they meet.
Acute angle : an angle which measures less than 90 degrees
The undefined terms are point and line.
Given, two line segments are equal to the third one
All the angles are equal to 60° each
By using Euclid’s axiom,
The things which are equal to the same thing are equal to one another.
Therefore, all the three sides of an equilateral triangle are equal.
Q.2. Study the following statement: “Two intersecting lines cannot be perpendicular to the same line”. Check whether it is an equivalent version to the Euclid’s fifth postulate.
[Hint: Identify the two intersecting lines l and m and the line n in the above statement.]
Given, the statement is “Two intersecting lines cannot be perpendicular to the same line”.
We have to determine an equivalent version to the Euclid’s fifth postulate.
Euclid’s fifth postulate states that if a straight line falling on two straight lines makes the interior angles on the same side of it, taken together less than two right angles, then the the two straight lines if produced indefinitely, meet on that side on which the sum of angles is taken together less than two right angles.
Two equivalent version to the Euclid’s fifth postulate are
1. For every line l and for every point P not lying on Z, there exists a unique line m passing through P and parallel to Z.
2. Two distinct intersecting lines cannot be parallel to the same line.
Therefore, the given statement is not an equivalent version to Euclid's fifth postulate.
Q.3. Read the following statements which are taken as axioms :
(i) If a transversal intersects two parallel lines, then corresponding angles are not necessarily equal.
(ii) If a transversal intersects two parallel lines, then alternate interior angles are equal.
Is this system of axioms consistent? Justify your answer
Given, the statements are
(i) If a transversal intersects two parallel lines, then corresponding angles are not necessarily equal.
(ii) If a transversal intersects two parallel lines, then alternate interior angles are equal
A system of axioms is called consistent , if there is no statement which can be deduced from these axioms such that it contradicts any axiom.The alternate interior angle theorem states that if a transversal intersects two parallel lines, then corresponding angles are equal.
From the figure,
∠1 = ∠5,
∠2 = ∠6
∠3 = ∠7
∠4 = ∠8
Therefore, the first statement is false and not an axiom.
The alternate interior angle theorem states that if a transversal intersects two parallel lines, then the alternate interior angles are equal.
Therefore, the second statement is true and an axiom.
Q.4. Read the following two statements which are taken as axioms
(i) If two lines intersect each other, then the vertically opposite angles are not equal.
(ii) If a ray stands on a line, then the sum of two adjacent angles so formed is equal to 180°.
Is this system of axioms consistent? Justify your answer
Given, the statements are
(i) If two lines intersect each other, then the vertically opposite angles are not equal.
(ii) If a ray stands on a line, then the sum of two adjacent angles formed is equal to 180°.
We have to determine if the system of axioms is consistent or not.
In a pair of intersecting lines, the vertically opposite angles are equal is a theoremFrom the figure,
∠AOD = ∠COB
∠AOC = ∠DOB
Therefore, the first statement is false and not an axiom.From the figure,
AB is a ray standing on a straight line CD.
AB is perpendicular to CD
The adjacent angles are right angles
∠B = ∠ABC + ∠ABD
= 90° + 90°
Total angle = 180°
Therefore, the second statement is true and an axiom.
Q.5. Read the following axioms:
(i) Things which are equal to the same thing are equal to one another.
(ii) If equals are added to equals, the wholes are equal.
(iii) Things which are double of the same thing are equal to one another.
Check whether the given system of axioms is consistent or inconsistent.
Given the statements are
(i) Things which are equal to the same thing are equal to one another.
(ii) If equals are added to equals, the wholes are equal.
(iii) Things which are double of the same thing are equal to one another.
We have to determine if the system of axioms is consistent or inconsistent.
A system of axioms is called consistent , if there is no statement which can be deduced from these axioms such that it contradicts any axiom.
According to Euclid’s first axiom,
The things which are equal to the same thing are equal to one another.
According to Euclid’s second axiom,
If equals are added to the equals, the wholes are equal.
According to Euclid’s sixth axiom,
Things which are double of the same thing are equal to one another.
We observe that the given statements are Euclid’s axioms.
We cannot deduce any statement from these axioms which contradicts any axiom.
Therefore, the given statements are consistent.
|
40 videos|470 docs|56 tests
|
FAQs on NCERT Exemplar Solutions: Introduction to Euclid's Geometry - Mathematics (Maths) Class 9
| 1. What is the significance of Euclid's geometry in mathematics? |  |
| 2. How can I understand the basic concepts of Euclidean geometry? |  |
| 3. What are the main differences between Euclidean and non-Euclidean geometry? |  |
| 4. How do the concepts of Euclid's geometry apply to real-world situations? |  |
| 5. What resources can help me study Euclid's geometry effectively? |  |