NCERT Exemplar Solutions: Playing with Numbers | Mathematics (Maths) Class 8 PDF Download
In each of the questions 1 to 17, out of the four options, only one is correct. Write the correct answer.
Q.1. Generalised form of a four-digit number abdc is
(a) 1000 a + 100 b + 10 c + d
(b) 1000 a + 100 c + 10 b + d
(c) 1000 a + 100 b + 10 d + c
(d) a × b × c × d
Ans: c
Solution: The correct answer is option (c) 1000 a + 100 b + 10 d + c
We know that, the numbers are expressed as the sum of the product of it digits with the respective place value. So the generalised form of abdc is 1000 a + 100 b + 10 d + c
Q.2. Generalised form of a two-digit number xy is
(a) x + y
(b) 10x + y
(c) 10x – y
(d) 10y + x
Ans: b
Solution: The correct answer is option (b) 10x + y
The numbers are expressed as the sum of the product of it digits with the respective place value. So the generalised form of xy is 10x+y
Q.3. The usual form of 1000a + 10b + c is
(a) abc
(b) abco
(c) aobc
(d) aboc
Ans: c
Solution: The correct answer is option (c) aobc
The usual form to represent the aobc is 1000xa+100xo+ 10xb+1xc, which is equal 1000a+10b+c
Q.4. Let abc be a three-digit number. Then abc – cba is not divisible by
(a) 9
(b) 11
(c) 18
(d) 33
Ans: c
Solution: The correct answer is option (c) 18
The general form of abc is 100a+10b+c
The genera form of cba is
Now (abc- cba) = (100a+10b+c ) – (100c+10b+a) =99a-99c
= 99(a – c)
Now, abc – cba is divisible by 99, because 99 is the factor of abc – cba
So, all the numbers which are the factors of 99 will also be divisible by abc-cba
Here, 9, 11 and 33 are the factors of 99. But 18 is not a factor of 99. Hence abc- cba is not divisible by 18.
Q.5. The sum of all the numbers formed by the digits x, y and z of the number xyz is divisible by
(a) 11
(b) 33
(c) 37
(d) 74
Ans: c
Solution: The correct answer is option (c) 37
It is known that, three numbers which can be formed by the using the digits x, y and z are xyz, yzx and zxy.
The general form of xyz = 100x + 10y + z.
The general form of yzx = 100y + 10z + x.
The general form of zxy = 100z + 10x + y.
Add the three numbers, we will get
xyz + yzx + zxy = (100x + 10y + z) + (100y + 10z + x) + (100z + 10x + y).
xyz + yzx + zxy = 100x + 10x + x + 100y + 10y + y + 100z + 10z + z
xyz + yzx + zxy = 111x + 111y + 111z.
Now, simplify the expression, we will get
xyz + yzx + zxy = 111(x + y + z).
Now, it is clear that 111 is the common factor. So,
xyz + yzx + zxy is divisible by 111
Also xyz + yzx + zxy will be divisible by factors of 111.
From the given options, 11, 33, and 74 are not the factors of 11 whereas 37 is the factor of 111.
Q.6. A four-digit number aabb is divisible by 55. Then possible value(s) of b is/are
(a) 0 and 2
(b) 2 and 5
(c) 0 and 5
(d) 7
Ans: c
Solution: It is known that if a number is divisible by 55, then the number should be divisible by the factors of 55
It means that the number aabb is divisible by 5. By using the divisibility test of 5, it must be 0 or 5.
Q.7. Let abc be a three digit number. Then abc + bca + cab is not divisible by
(a) a + b + c
(b) 3
(c) 37
(d) 9
Ans: d
Solution: By simplifying the general form of abc, bca and cab, we will get
= abc+bca+cab = 111(a+b+c)
Hence, abc+bca+cab is divisible by 111 and also it is divisible by the factors of 111.
Here, 3 and 7 are the factors of 111, and a+b+c is also a factor of 111(a+b+c).
But 9 is not the factor of 111.
Q.8. A four-digit number 4ab5 is divisible by 55. Then the value of b – a is
(a) 0
(b) 1
(c) 4
(d) 5
Ans: b
Solution: We know that the four digit number 4ab5 which is divisible by 55 is also divisible by 11 and also the factors of it. By using the divisibility test of 11, the difference between the sum of the alternate digits should be a multiple of 11.
It means that
(4+b) – (a+5) =0, 11, 22, …it becomes
b – a – 1 = 0
Hence, b – a = 1
Q.9. If abc is a three digit number, then the number abc – a – b – c is divisible by
(a) 9
(b) 90
(c) 10
(d) 11
Ans: a
Solution: We know that the general form of abc is 100a+10b+c
Then the given number is abc – a – b – c =100a+10b+c – a – b- c
By simplifying the above expression, we will get
abc – a – b – c = 9(11a+b)
Hence, then number abc – a – b – c is divisible by 9.
Q.10. A six-digit number is formed by repeating a three-digit number. For example 256256, 678678, etc. Any number of this form is divisible by
(a) 7 only
(b) 11 only
(c) 13 only
(d) 1001
Ans: d
Solution: From the given question, the number should be of the form abcabc
So the general form of abcabc is 1000000a+100000b+1000c+100a+10b+c
Now, abcabc = is 1000000a+100000b+1000c+100a+10b+c
By simplifying the above expression, we will get
abcabc = 1001(100a+10b+c)
Hence, the six digit number should be divisible by 1001.
Q.11. If the sum of digits of a number is divisible by three, then the number is always divisible by
(a) 2
(b) 3
(c) 6
(d) 9
Ans: b
Solution: The option (b) – 3 is the correct answer because the divisibility test of 3 says that the sum of the digits of a number is divisible by 3, then the number is always divisible by 3.
Q.12. If x + y + z = 6 and z is an odd digit, then the three-digit number xyz is
(a) an odd multiple of 3
(b) odd multiple of 6
(c) even multiple of 3
(d) even multiple of 9
Ans: a
Solution: Given that, the sum of the digits xyz is given as x+y+z is 6, where z is an odd integer.
The divisibility test of 3, the number xyz is divisible by z. Since the last digit is an odd digit, then xyz is an odd multiple of 3.
Q.13. If 5 A + B 3 = 65, then the value of A and B is
(a) A = 2, B = 3
(b) A = 3, B = 2
(c) A = 2, B = 1
(d) A = 1, B = 2
Ans: c
Solution:
In the 1’s column A +3 = 5
When A is added with 3, it gives 5
Since A is a digit, it should be between 0 and 9
When you substitute A = 2, you will get 2+3 = 5
Similarly, repeat the process for 10’s column
Then we will get B= 1
Therefore A= 2, and B = 1
Q.14. If A 3 + 8 B = 150, then the value of A + B is
(a) 13
(b) 12
(c) 17
(d) 15
Ans: a
Solution: From the question,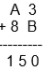
In 1’s place, we have to add 3+B = 0
Since B is a digit, the value of B should between 0 and 9
When you substitute the value of B = 7, then you will get
3+7 = 10
So here the unit digit is 0.
Now carry 1 to the 10’ s place,
Repeat the same process for 10’s place, you will get the value of A
So, A = 6
Therefore, A+B = 6+7 = 13
Q.15. If 5 A × A = 399, then the value of A is
(a) 3
(b) 6
(c) 7
(d) 9
Ans: c
Solution: In the 1’s place, the product of A and A gives 9
Here, A is a number whose multiplication gives the two digit number having 9 in its 1’s place.
So, the product of 7 and 7 gives 49, where 1’s place is 9.
Q.16. If 6 A × B = A 8 B, then the value of A – B is
(a) –2
(b) 2
(c) –3
(d) 3
Ans: a
Solution: Given that, 6 A × B = A 8 B
So, AB = B
Therefore A = 1
Now substitute A = 1 in the given equation
6B = A8
6B = 18
B = 18/6 = 3
Now, A – B = 1 -3 = -2
Q.17. Which of the following numbers is divisible by 99
(a) 913462
(b) 114345
(c) 135792
(d) 3572406
Ans: b
Solution: If a number is divisible is 99, it should be divisible by both 9 and 11.
From the given option, option (b) 114345 is divisible by both 9 and 11.
All other numbers are either divisible by 9 or 11,but not both 9 and 11.
In questions 18 to 33, fill in the blanks to make the statements true.
Q.18. 3134673 is divisible by 3 and ______.
Ans: 9
Adding all the digits in the given number, we get 27, which is divisible by 3 and 9.
Q.19. 20×3 is a multiple of 3 if the digit x is ______ or ______ or ______.
Ans: 1 or 4 or 7
It is known that, when a number is a multiple of 3, if the sum of digits in the number is a multiple of 3
By equating the closet multiple of 3 such as 6, 9, and 12, we get the digit
Either the digit x should be 1 or 4 or 7.
Q.20. 3×5 is divisible by 9 if the digit x is ______.
Ans: 1
It is known that, if a number is a multiple of 9, then the sum of digits of a number is divisible by 9.
From, the given equation, we can write it as:
3+x+5 = x + 8
It means that x+8 is divisible by 8, if x+8 is equal to 9,
Then the value of x is 1.
Q.21. The sum of a two–digit number and the number obtained by reversing the digits is always divisible by ______.
Ans: 11
Let “a” and “b” be the digits, then X = ab
By reversing the digits, then take Y =ba
Therefore sum of digits in X is 10a+b
Sum of digits in Y is 10b+a
By adding X and Y, we get
11a+11b = 11(a+b)
Therefore, the number is divisible by 11.
Q.22. The difference of a two–digit number and the number obtained by reversing its digits is always divisible by ______.
Ans: 9
Let “a” and “b” be the digits, then X = ab
By reversing the digits, then take Y =ba
Therefore sum of digits in X is 10a+b
Sum of digits in Y is 10b+a
By subtracting X and Y, we get
9a – 9a = 9(ab)
Therefore, the number is divisible by 9.
Q.23. The difference of three-digit number and the number obtained by putting the digits in reverse order is always divisible by 9 and ______.
Ans: 11
Let “a”, “b” and “c” be the digits, then X = abc
By reversing the digits, then take Y =cba
Therefore sum of digits in X is 100a+10b+c
Sum of digits in Y is 100c+10b+a
By subtracting X and Y, we get
99(x-z) = (9)(11)(x-z)
Therefore, the number is divisible by 9 and 11.
Q.24. If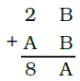 , then A = ______ and B = ______.
, then A = ______ and B = ______.
Ans: A = 6 and B= 3
By adding the given digit according to the place value,
20+B + 10 A +B = 80 +A
9A+2B = 60
9A = 60 -2B
As, both A and B are whole numbers, 60-2B should be divisible by 9
So, the value of B should be 3
Substitute B = 3 in 9A + 2B = 60
Simplifying this, we will get
A = 6.
Q.25. If 
, then A = ___________ and B = ___________
Ans: A = 2 and B = 4
From the question, it is given that the units place contains a 6. So, the product of B and B should give a number with 6 in units place. It is possible when B = 4 or 6.
When B = 4,
(10A + B) x (B) = 96
It becomes (10A + 4) x 4 = 96
40A + 16 = 96,
By simplifying the equation, it gives A = 2.
Similarly, when B = 6,
(10A + B)x(B) = 96
By simplifying, it becomes (10A + 6) x 6 = 96
60A + 36 = 96, gives A = 1.
Hence, A = 2 B = 4 or A = 1 B = 6 (Both are feasible solutions)
Q.26. If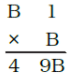 , then B = ______.
, then B = ______.
Ans: B = 7
From the question, it is clear that the value of B should be greater than 4 and less than 9.
If the B value is less than 4, the solution should have only two digits. If the B value is greater than 9, the solution should have more than 3 digit.
So, the value of B ranges from 4 to 9. The 10’s place when multiplied by B gives 49
Hence, B x B = 49
Therefore, B = 7
Q.27. 1 x 35 is divisible by 9 if x = _______.
Ans: 0
We know that, when a number is a multiple of 9, then the sum of digits in the number is divisible by 9
So, by adding the digits, we get:
X+9 = 9
Hence, x = 0
Q.28. A four-digit number abcd is divisible by 11, if d + b = _______ or _______.
Ans: a+c or b+d
Using the divisibility rule of 11, if abcd is divisible by 11, then
a-b + c-d = 0
By rearranging the terms, we get
a+ c = b+ d, or each should be zero
Q.29. A number is divisible by 11 if the differences between the sum of digits at its odd places and that of digits at the even places is either 0 or divisible by ______.
Ans: 11
Assume that the four digit number abcd
Here, the digits at odd places are a and c and in even places are b and d
Hence, (a+c) – (b+d) = 0
It follows that, (a+c) – (b+d) is divisible by 11, when (a+c) – (b+d) is not equal to 0.
Q.30. If a 3-digit number abc is divisible by 11, then ______ is either 0 or multiple of 11.
Ans: (a+c)-b
From the direct consequence from the divisibility rule of 11, we say that (a+c)- b is either 0 or a multiple of 11.
Q.31. If A × 3 = 1A, then A = ______.
Ans: 5
Using the place values of the numbers, we can write it as:
10 + A = 3A
10 = 2A
A = 5
Q.32. If B × B = AB, then either A = 2, B = 5 or A = ______, B = ______.
Ans: A= 1 and B= 6
From the given equations, B can take the values between 4 and 9
When you take B = 4, 4×4 = 16
Then, A=1 and B = 6
Q.33. If the digit 1 is placed after a 2-digit number whose tens is t and one’s digit is u, the new number is ______.
Ans: tu1
Assume that, the number is initially 10t+u or tu, but after adding 1 to the unit place, tu gets shifted to the one unit higher. It means that 100t+10u+1 or tu1.
State whether the statements given in questions 34 to 44 are true (T) or false (F):
Q.34. A two-digit number ab is always divisible by 2 if b is an even number.
Ans: True
If a number with two digits and the number in the unit place is even, then the number is said to be an even number and it is divisible by 2 (using the divisibility test of 2)
Q.35. A three-digit number abc is divisible by 5 if c is an even number.
Ans: False
If a number with three digits and if the unit digit is an even number, then the number is said to be an even number. A number is divisible by 5, only if the unit digit is either 0 or 5 (divisibility test of 5)
Q.36. A four-digit number abcd is divisible by 4 if ab is divisible by 4.
Ans: False
Assume that 2463 is a four digit number which is equal to abcd.
We know that 24 is divisible by 4, but 2463 is not divisible by 4.
Q.37. A three-digit number abc is divisible by 6 if c is an even number and
a + b + c is a multiple of 3.
Ans: True
In case, if a number is divisible by 6, it is also divisible by 2 and 3.
If c is an even number, then the sum of digits is divisible by 3.
Q.38. Number of the form 3N + 2 will leave remainder 2 when divided by 3.
Ans: True
The given number is of the form 3N+2
It can be written as (multiples of 3) + 2
When the given number 3N+2 is divide by 3, we will get the remainder 2. For example take 11.
11 can be written as (3×3) + 2
Q.39. Number 7N + 1 will leave remainder 1 when divided by 7.
Ans: True
The given number is of the form 7N+1
It can be written as (multiples of 7) + 1
When the given number 7N+1 is divide by 7, we will get the remainder 1. For example take 22.
22 can be written as (7×3) + 1
Q.40. If a number a is divisible by b, then it must be divisible by each factor of b.
Ans: True
Let a= 27, and b = 9
Here, when 27 is divisible by 9, we will get 3
Now, consider the factor of 9 = 1, 3 and 9
In this case, 27 is divisible by the factors such as 1 and 3. Hence the given statement is true.
Q.41. If AB × 4 = 192, then A + B = 7.
Ans: False
From the given question, the value of B should be either 3 or 8.
If you take the value of B is 3, it should be equal to 19.
Hence, the value of B is 8.
We know that, the value of A should between 0 and 9.
Hence, A x 4 = 19- 3 = 16
A = 16/4
A = 4
Therefore A= 4 and B= 8
Hence, A+B = 4+8 = 12
Q.42. If AB + 7C = 102, where B ≠ 0, C ≠ 0, then A + B + C = 14.
Ans: True
From the given number, B+C is either 2 or the two digit number that gives the unit digit as 2.
It is given that B ≠ 0, C ≠ 0,
If B or C = 5 or 7, then A should be 3, then it becomes A+B+C = 14
Or else, if B= C = 6, and A = 2, we will get A+B+C = 14
Q.43. If 213x 27 is divisible by 9, then the value of x is 0.
Ans: False
If 213 x 27 is divisible by 9, then the sum of the digits of a number is a multiple of 9.
2+1+3+x+2+7 = 15+x
Then 15x must be any multiple of 9 such as 9, 18, 27 …
Now assume that,
15+x = 18
X = 18 -15
X = 3
Q.44. If N ÷ 5 leaves remainder 3 and N ÷ 2 leaves remainder 0, then N ÷ 10 leaves remainder 4.
Ans: False
Given that, when N is divided by 5, it leaves the remainder 5. (i.e) N = 5n+3 where n= 0, 1, 2, 3, …
Similarly, when N is divided by 2, it leaves the remainder 0. So N is an even Number. (Using divisibility test rule of 2).
But in N = 5n+3, the second term is odd.
So, 5n is an odd number.
When you substitute n = 1, 3, 5 … in 5n+3, we will get 8, 18, 28 …
Now, if we divide N by 10, it should be written as
N = 10 n+8
So, when N is divided by 10, it always leaves the remainder 8.
Solve the following:
Q.45. Find the least value that must be given to number a so that the number 91876a2 is divisible by 8.
Ans: a = 3
By using the divisibility test of 8, if a number is divisible by 8, then the last three digit of a number should be divisible by 8.
In the given question, the last three digit is 6a2.
The value of “a” varies from 0 to 9.
If a = 0, then 6a2 = 602 is not divisible by 8.
If a = 1, then 612 = 612 is not divisible by 8.
If a = 2, then 6a2 = 622 is not divisible by 8.
If a = 3, then 6a2 = 632 is divisible by 8.
Hence, the least value of “a” is 3.
|
81 videos|423 docs|31 tests
|
















