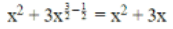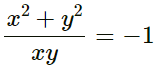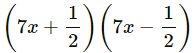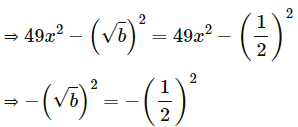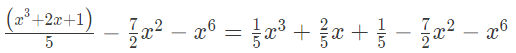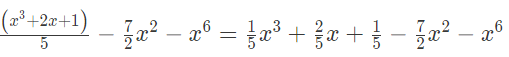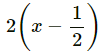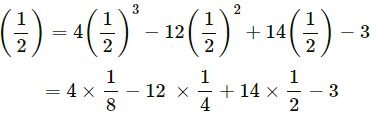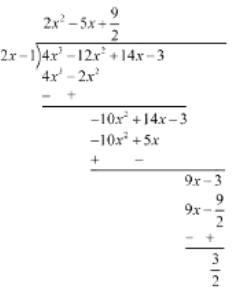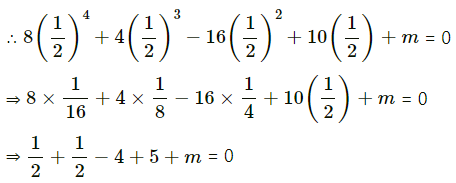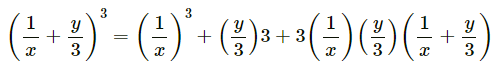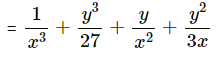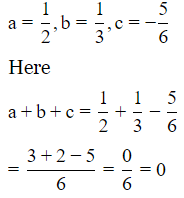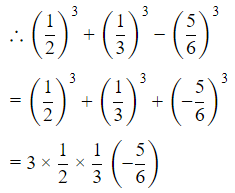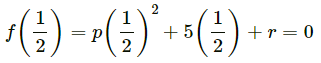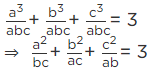NCERT Exemplar Solutions: Polynomials | Mathematics (Maths) Class 9 PDF Download
| Table of contents |

|
| Exercise 2.1 |

|
| Exercise 2.2 |

|
| Exercise 2.3 |

|
| Exercise 2.4 |

|
Exercise 2.1
Write the correct answer in each of the following:
Q.1. Which one of the following is a polynomial?
(a) 
(b) 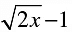
(c) 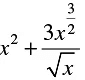
(d) 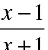
Correct Answer is option (c)
The power of x must be a non-negative integer in a polynomial.
Hence, option C is correct.
As we can write option c as
Q.2. √2 is a polynomial of degree
(a) 2
(b) 0
(c) 1
(d) 1/2
Correct Answer is option (b)
We can write it as √2 = √2 × x0
Thus, degree is 0.
Q.3. Degree of the polynomial 4x4 + 0x3 + 0x5 + 5x + 7 is
(a) 4
(b) 5
(c) 3
(d) 7
Correct Answer is option (a)
Degree of the polynomial 4x4 + 0x3 + 0x5 + 5x + 7 is 4
We know that, the degree of given polynomial 4x4 + 0 x x3 + 0 x x5 + 5x + 7 will be the highest power of variable that is 4.
Q.4. Degree of the zero polynomial is
(a) 0
(b) 1
(c) Any natural number
(d) Not defined
Correct Answer is option (d)
The degree of a polynomial is the highest degree of its monomials (individual terms) with non-zero coefficients. The degree of a term is the sum of the exponents of the variables that appear in it, and thus is a non-negative integer.Degree of zero polynomial is thus not-defined.
Q.5. If p (x ) = x2 –2√2 x+ 1 , then p(2√2) is equal to
(a) 0
(b) 1
(c) 4√2
(d) 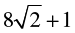
Correct Answer is option (b)
p(x) = x2 −2√2 x + 1
p(2√2 ) = (2√2)2 − 2√2 × 2√2 +1
p(2√2) = 8 − 8 + 1
p(2√2) = 1
Hence, option B.
Q.6. The value of the polynomial 5x – 4x2 + 3, when x = –1 is
(a) - 6
(b) 6
(c) 2
(d) - 2
Correct Answer is option (a)
Given that: a polynomial as
P(x) = 5x − 4x2 + 3
To find value of polynomial at x = −1 or P(−1)
So we put x = −1 in polynomial,
P(−1) = 5 × (−1) − 4 × (−1)2 + 3
P(−1) = − 5 − 4 + 3
P(−1) = − 6
So value of polynomial at x = − 1 is − 6.
Q.7. If p(x) = x + 3, then p(x) + p(–x) is equal to
(a) 3
(b) 2x
(c) 0
(d) 6
Correct Answer is option (d)
Given, p(x) = x + 3
Therefore, p(−x) = −x + 3
Now, p(x) + p(−x) = (x+3) + (−x+3) = 6
Option D is correct.
Q.8. Zero of the zero polynomial is
(a) 0
(b) 1
(c) Any real number
(d) Not defined
Correct Answer is option (c)
Zero of the polynomial is any real number .e.g., Let us consider zero polynomial be 0(x-k), where k is a real number for determining the zero
Put x − k = 0 ⇒ x = k
Hence, zero of the zero polynomial be any real number.
Q.9. Zero of the polynomial p(x) = 2x + 5 is
(a) -(2/5)
(b) -(5/2)
(c) 2/5
(d) 5/2
Correct Answer is option (b)
Zero of a polynomial is the value of the variable for which the polynomial becomes 0.
Now, p(x) = 2x + 5.
For, p(x) = 0,
2x + 5 = 0.
or, x = −5/2.
Therefore, option B is correct.
Q.10. One of the zeroes of the polynomial 2x2 + 7x –4 is
(a) 2
(b) 1/2
(c) -(1/2)
(d) –2
Correct Answer is option (b)
To find the zero of 2x 2 +7x−4 is same as solving the equation 2x2 + 7x − 4 = 0
⇒ 2x2 + 8x − x − 4 = 0
⇒ 2x(x+4) − 1(x+4) = 0
⇒ (2x−1)(x+4) = 0
⇒ (2x−1) = 0, (x + 4) = 0
⇒ x = 1/2 , −4
Therefore, option B is correct.
Q.11. If x51 + 51 is divided by x + 1, the remainder is
(a) 0
(b) 1
(c) 49
(d) 50
Correct Answer is option (d)
By remainder theorem,Remainder =p(−1), since the divisor is x+1
p(x) = x 51 + 51
p(−1) = (−1)51 + 51 = −1 + 51
Hence, the remainder is 50
Q.12. If x + 1 is a factor of the polynomial 2x2 + kx, then the value of k is
(a) –3
(b) 4
(c) 2
(d) –2
Correct Answer is option (c)
(x + 1) is a factor of p (x)
x + 1 = 0
⇒ x = − 1
Therefore, p (− 1) = 0
∴ 2 (− 1)2 + k(− 1) = 0
⇒ 2 − k = 0 ⇒ k = 2
Hence, the value of k is 2.
Q.13. x + 1 is a factor of the polynomial
(a) x3 + x2 – x + 1
(b) x3 + x2 + x + 1
(c) x4 + x3 + x2 + 1
(d) x4 + 3 x3 + 3x2 + x + 1
Correct Answer is option (b)
We know that if x + a is a factor of f(x) then, f(-a) = 0.
Let f(x) = x3 + x2 + x + 1
Now, f(-1) = (-1)3 + (-1)2 + (-1) + 1
= -1 + 1 - 1 + 1
= 0 = 0
So, f(x) is a factor of x + 1.
Q.14. One of the factors of (25x2 – 1) + (1 + 5x)2 is
(a) 5 + x
(b) 5 – x
(c) 5x – 1
(d) 10x
Correct Answer is option (d)
(25x2 – 1) + (1 + 5x)2
= 25x2 − 1 + 1 + 25x2 + 10 x [Using identity, (a + b)2 = a2 + b2 + 2ab]
= 50x2 + 10 x = 10 x (5x + 1)
Hence, one of the factor of given polynomial is 10x.
Q.15. The value of 2492 – 2482 is
(a) 12
(b) 477
(c) 487
(d) 497
Correct Answer is option (d)
We know, a2 −b2 = (a + b) (a − b)
So, 2492 −2482 = (249 + 248) (249 − 248) = 497(1) = 497
Q.16. The factorisation of 4x2 + 8x + 3 is
(a) (x + 1) (x + 3)
(b) (2x + 1) (2x + 3)
(c) (2x + 2) (2x + 5)
(d) (2x –1) (2x –3)
Correct Answer is option (b)
4x2 + 8x + 3
⇒ 4x2 + 6x + 2x + 3
⇒ 2x(2x+3) + 1(2x+3)
⇒ (2x+3) (2x+1)
Q.17. Which of the following is a factor of (x + y)3 – (x3 + y3)?
(a) x2 + y2 + 2 xy
(b) x2 + y2 – xy
(c) xy2
(d) 3xy
Correct Answer is option (d)
(x + y)3 −(x3 + y3)
= x3 + y3 + 3xy(x+y) − x3 − y3
= 3xy(x+y)
Hence, 3xy and (x+y) are the factors of the equation
Q.18. The coefficient of x in the expansion of (x + 3)3 is
(a) 1
(b) 9
(c) 18
(d) 27
Correct Answer is option (d)
Now, (x + 3)3 = x3 + 33 + 3x (3)(x + 3)
[using identity, (a + b)3 = a3 + b3+ 3ab (a + b)]
= x3 + 27 + 9x (x + 3)
= x3 + 27 + 9x2 + 27x
Hence, the coefficient of x in (x + 3)3 is 27.
Q.19. If 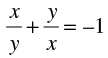 (x, y ≠ 0) , the value of x3 – y3 is
(x, y ≠ 0) , the value of x3 – y3 is
(a) 1
(b) –1
(c) 0
(d) 1/2
Correct Answer is option (c)
Consider the equation:
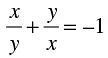
Simplify the above expression as follows:
x2 + y2 = -xy
Now, x3 - y3 = (x-y) (x2+y2 + xy)
= (x-y)(-xy + xy) ...... [Substitute: x2 + y2 = –xy]
= (x-y) × 0
= 0
Q.20. If 49x2 – b = 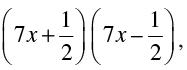 then the value of b is
then the value of b is
(a) 0
(b) 1/√2
(c) 1/4
(d) 1/2
Correct Answer is option (c)
Given (49x2 – b) =
......[Using identity, (a + b)(a – b) = a2 – b2]
⇒ (√b)2 = (1/2)2 ...... [Multiplying both sides by –1]
∴ b = 1/4
Q.21. If α + b + c = 0, then α3 + b3 + c3 is equal to
(a) 0
(b) αbc
(c) 3αbc
(d) 2αbc
Correct Answer is option (c)
Since, α3 + b3 + c3 −3αbc = (a + b + c)(a2 + b2 + c2 −bc − ca − ab)
Given, a + b + c = 0
∴ a3 + b3 + c3 − 3abc = 0
∴ a3 + b3 + c3 = 3abc
Option b is correct.
Exercise 2.2
Q.1. Which of the following expressions are polynomials? Justify your answer:
(i) 8
Polynomial. Because, the exponent of the variable of 8 or 8x0 is 0 which is a whole number.
(ii) 
Polynomial. Because, the exponent of the variable of
is a whole number.
(iii) 1 - √5x
Not a polynomial. Because, the exponent of the variable of 1 − √5x or 1 − √5x1/2 is 1/2 which is not a whole number.
(iv) 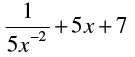
Polynomial. Because, the exponents of the variable of
= 1/5x2 + 5x + 7 are whole numbers.
(v) 
Not a polynomial. Because, the exponent of the variable of
= x − 6 + 8x−1 is -1, which is not a whole number.
(vi) 1/x+1
Not a polynomial as the polynomial is expressed as a0 + a1x + a2xn , where a0 , a1 , a2 ⋯ , an are constants. Now, the given function is in the form f(x) = p(x)/q(x) is a rational expression but not a polynomial.
(vii) 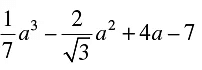
Polynomial. Because, the exponents of the variable of
+ 4 a − 7 are whole numbers.
(viii) 1/2x
Not a polynomial. Because, the exponent of the variable of 1/2x or 1/2x-1 is -1, which is not a whole number.
Q.2. Write whether the following statements are True or False. Justify your answer.
(i) A binomial can have at most two terms
False
because a binomial has exactly two terms.
(ii) Every polynomial is a binomial
False
x3 + x + 1 is a polynomial but not a binomial.
(iii) A binomial may have degree 5
True
because a binomial is a polynomial whose degree is a whole number ≥ 1, so, degree can be 5 also.
(iv) Zero of a polynomial is always 0
False
because zero of a polynomial can be any real number.
(v) A polynomial cannot have more than one zero
False
A polynomial can have any number of zeroes. It depends upon the degree of the polynomial.
(vi) The degree of the sum of two polynomials each of degree 5 is always 5.
False
x5 + 1 and – x5 + 2 x + 3 are two polynomials of degree 5 but the degree of the sum of the two polynomials is 1.
Exercise 2.3
Q.1. Classify the following polynomials as polynomials in one variable, two variables etc.
(i) x2 + x + 1
Here, the polynomial contains only one variable, i.e., x. Hence, the given polynomial is a polynomial in one variable.
(ii) y3 – 5 y
Here, the polynomial contains only one variable, i.e., y. Hence, the given polynomial is a polynomial in one variable.
(iii) xy + yz + zx
Here, the polynomial contains three variables, i.e., x, y and z. Hence, the given polynomial is a polynomial in three variable.
(iv) x2 – 2 xy + y2 + 1
Here, the polynomial contains two variables, i.e., x and y. Hence, the given polynomial is a polynomial in two variable.
Q.2. Determine the degree of each of the following polynomials:
(i) 2x – 1
Degree of a polynomial in one variable = highest power of the variable in algebraic expression
Highest power of the variable x in the given expression = 1 Hence, degree of the polynomial 2x – 1 = 1
(ii) –10
There is no variable in the given term.
Let us assume that the variable in the given expression is x.
– 10 = –10x0
Power of x = 0
Highest power of the variable x in the given expression = 0 Hence, degree of the polynomial – 10 = 0
(iii) x3 – 9 x + 3 x5
Powers of x = 3, 1 and 5 respectively.
Highest power of the variable x in the given expression = 5 Hence, degree of the polynomial x3 – 9x + 3x5 = 5
(iv) y3 (1 – y4)
The equation can be written as, y3(1 – y4) = y3 – y7
Powers of y = 3 and 7 respectively.
Highest power of the variable y in the given expression = 7 Hence, degree of the polynomial y3(1 – y4) = 7
Q.3. For the polynomial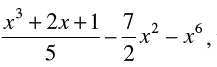 write
write
(i) the degree of the polynomial
Powers of x = 3, 1, 2 and 6 respectively.
Highest power of the variable x in the given expression = 6 Hence, degree of the polynomial = 6
(ii) the coefficient of x3
The given equation can be written as,
Hence, the coefficient of x3 in the given polynomial is 1/5.
(iii) the coefficient of x6
The coefficient of x6 in the given a polynomial is – 1
(iv) the constant term
Since the given equation can be written as,
The constant term in the given polynomial is 1/5 as it has no variable x associated with it.
Q.4. Write the coefficient of x2 in each of the following :
(i) (π/6)x + x2 – 1
(π/6) x + x2−1 = (π/6) x + (1) x2−1
The coefficient of x2 in the polynomial (π/6) x + x2−1 = 1.
(ii) 3x – 5
3x – 5 = 0x2 + 3x – 5
The coefficient of x2 in the polynomial 3x – 5 = 0, zero.
(iii) (x –1) (3x – 4)
(x – 1)(3x – 4) = 3x2 – 4x – 3x + 4
= 3x2 – 7x + 4
The coefficient of x2 in the polynomial 3x2 – 7x + 4 = 3.
(iv) (2x – 5) (2x2 – 3x + 1)
(2x – 5) (2x2 – 3x + 1)
= 4x3 – 6x2 + 2x – 10x2 + 15x– 5
= 4x3 – 16x2 + 17x – 5
The coefficient of x2 in the polynomial (2x – 5) (2x2 – 3x + 1) = – 16
Q.5. Classify the following as a constant, linear, quadratic and cubic polynomials:
(i) 2 – x2 + x3
Powers of x = 2, and 3 respectively.
Highest power of the variable x in the given expression = 3 Hence, degree of the polynomial = 3
Since it is a polynomial of the degree 3, it is a cubic polynomial.
(ii) 3x3
Power of x = 3.
Highest power of the variable x in the given expression = 3
Hence, the degree of the polynomial = 3
Since it is a polynomial of the degree 3, it is a cubic polynomial.
(iii) 5t – √7
Power of t = 1.
Highest power of the variable t in the given expression = 1 Hence, degree of the polynomial = 1
Since it is a polynomial of the degree 1, it is a linear polynomial.
(iv) 4 – 5y2
Power of y = 2.
Highest power of the variable y in the given expression = 2 Hence, degree of the polynomial = 2
Since it is a polynomial of the degree 2, it is a quadratic polynomial.
(v) 3
There is no variable in the given expression.
Let us assume that x is the variable in the given expression. 3 can be written as 3x0.
i.e., 3 = x0 Power of x = 0.
Highest power of the variable x in the given expression = 0 Hence, degree of the polynomial = 0
Since it is a polynomial of the degree 0, it is a constant polynomial.
(vi) 2 + x
Power of x = 1.
Highest power of the variable x in the given expression = 1 Hence, degree of the polynomial = 1
Since it is a polynomial of the degree 1, it is a linear polynomial.
(vii) y3 – y
Powers of y = 3 and 1, respectively.
Highest power of the variable x in the given expression = 3 Hence, degree of the polynomial = 3
Since it is a polynomial of the degree 3, it is a cubic polynomial.
(viii) 1 + x + x2
Powers of x = 1 and 2, respectively.
Highest power of the variable x in the given expression = 2 Hence, degree of the polynomial = 2
Since it is a polynomial of the degree 2, it is a quadratic polynomial.
(ix) t2
Power of t = 2.
Highest power of the variable t in the given expression = 2
Hence, the degree of the polynomial = 2
Since it is a polynomial of the degree 2, it is a quadratic polynomial.
(x) √2x – 1
Power of x = 1.
Highest power of the variable x in the given expression = 1 Hence, degree of the polynomial = 1
Since it is a polynomial of the degree 1, it is a linear polynomial.
Q.6. Give an example of a polynomial, which is:
(i) monomial of degree 1
Monomial = an algebraic expression that contains one term
An example of a polynomial, which is a monomial of degree 1 = 2t
(ii) binomial of degree 20
Binomial = an algebraic expression that contains two terms
An example of a polynomial, which is a binomial of degree 20 = x20 + 5
(iii) trinomial of degree 2
Trinomial = an algebraic expression that contains three terms
An example of a polynomial, which is a trinomial of degree 2 = y2 + 3y + 11
Q.7. Find the value of the polynomial 3x3 – 4x2 + 7 x – 5, when x = 3 and also when x = –3.
Given that,
p(x) = 3𝑥3 – 4𝑥2 + 7𝑥 – 5 According to the question, When x = 3,
p(x) = p(3)
p(x) = 3𝑥3 – 4𝑥2 + 7𝑥 – 5 Substituting x = 3,
p(3)= 3(3)3 – 4(3)2 + 7(3) – 5
p(3) = 3(3)3 – 4(3)2 + 7(3) – 5
= 3(27) – 4(9) + 21 – 5
= 81 – 36 + 21 – 5
= 102 – 41
= 61
When x = – 3, p(x) = p(– 3)
p(x) = 3𝑥3 – 4𝑥2 + 7𝑥 – 5 Substituting x = – 3,
p(– 3)= 3(– 3)3 – 4(– 3)2 + 7(– 3) – 5
p(– 3) = 3(–3)3 – 4(–3)2 + 7(–3) – 5
= 3(–27) – 4(9) – 21 – 5
= –81 – 36 – 21 – 5 = –143
Q.8. If p(x) = x2 – 4 x + 3, evaluate : p(2) – p(–1) + p(1/2)
Given that,
p(𝑥) = 𝑥2 – 4𝑥 + 3
According to the question, When x = 2,
p(x) = p(2)
p(𝑥) = 𝑥2 – 4𝑥 + 3
Substituting x = 2,
p(2) = (2)2 – 4(2) + 3
= 4 – 8 + 3
= – 4 + 3
= – 1
When x = – 1, p(x) = p(– 1) p(𝑥) = 𝑥2 – 4𝑥 + 3
Substituting x = – 1,
p(– 1) = (– 1)2 – 4(– 1) + 3
= 1 + 4 + 3
= 8
When x = 1/2 , p(x) = p(1/2)
p(𝑥) = 𝑥2 – 4𝑥 + 3
Substituting x = 1/2,
p(1/2) = (1/2)2 – 4(1/2) + 3
= 1/4 – 2 + 3
= 1/4 + 1
= 5/4
Now,
p(2)− p(−1) + p(1/2) = – 1 – 8 + (5/4)
= – 9 + (5/4)
= ( – 36 + 5)/4
= – 31/4
Q.9. Find p(0), p(1), p(–2) for the following polynomials:
(i) p(x) = 10x – 4 x2 – 3
According to the question, p(x) = 10𝑥−4𝑥2 –3
When x = 0, p(x) = p(0)
Substituting x = 0,
p(0) = 10(0)−4(0)2 –3
= 0 – 0 – 3
= – 3
When x = 1, p(x) = p(1)
Substituting x = 1,
p(1) = 10(1) − 4(1)2 –3
= 10 – 4 – 3
= 6 – 3
= 3
When x = – 2, p(x) = p(– 2)
Substituting x = – 2,
p(– 2) = 10(– 2) − 4(– 2)2 –3
= – 20 – 16 – 3
= – 36 – 3
= – 39
(ii) p(y) = (y + 2) (y – 2)
According to the question, p(𝑦) = (y + 2) (y – 2)
When y = 0, p(y) = p(0)
Substituting y = 0, p(0) = (0 + 2) (0 – 2)
= (2)(– 2)
= – 4
When y = 1, p(y) = p(1)
Substituting y = 1, p(1)=(1 + 2) (1 – 2)
=(3) (– 1)
= – 3
When y = – 2, p(y) = p(– 2)
Substituting y = – 2,
p(– 2) =(– 2 + 2) (– 2 – 2)
= (0) (– 4)
= 0
Q.10. Verify whether the following are true or false:
(i) –3 is a zero of x – 3
False
Zero of x – 3 is given by, x – 3 = 0
⇒ x=3
(ii) – 1/3 is a zero of 3x + 1
True
Zero of 3x + 1 is given by, 3x + 1 = 0
⇒ 3x = – 1
⇒ x = – 1/3
(iii) – 4/5 is a zero of 4 –5y
False
Zero of 4 – 5y is given by, 4 – 5y =0
⇒ – 5y = – 4
⇒ y = 4/5
(iv) 0 and 2 are the zeroes of t2 – 2t
True
Zeros of t2 – 2t is given by, t2 – 2t = t(t – 2) = 0
⇒ t = 0 or 2
(v) –3 is a zero of y2 + y – 6
Zero of y2 + y – 6 is given by, y2 + y – 6 = 0
⇒ y2 + 3x – 2x – 6 = 0
⇒ y(y + 3) – 2(x + 3) = 0
⇒ (y – 2) (y + 3) = 0
⇒ y = 2 or – 3
Q.11. Find the zeroes of the polynomial in each of the following :
(i) p(x) = x – 4
Zero of the polynomial p(x) ⇒ p(x) = 0
P(x) = 0
⇒ x – 4 = 0
⇒ x = 4
Therefore, the zero of the polynomial is 4.
(ii) g(x) = 3 – 6x
Zero of the polynomial g(x) ⇒ g(x) = 0 g(x) = 0
⇒3 – 6x = 0
⇒ x = 3/6 =1/2
Therefore, the zero of the polynomial is 1/2
(iii) q(x) = 2x –7
Zero of the polynomial q(x) ⇒ q(x) = 0 q(x) = 0
⇒2x – 7 = 0
⇒ x = 7/2
Therefore, the zero of the polynomial is 7/2
(iv) h(y) = 2y
Zero of the polynomial h(y) ⇒ h(y) = 0 h(y) = 0
⇒ 2y = 0
⇒ y = 0
Therefore, the zero of the polynomial is 0
Q.12. Find the zeroes of the polynomial : p(x) = (x – 2)2 – ( x + 2)2
We know that,
Zero of the polynomial p(x) = 0
Hence, we get,
⇒ (x–2)2 − (x + 2)2 = 0
Expanding using the identity, a2 – b2 = (a – b) (a + b)
⇒ (x – 2 + x + 2) (x – 2 –x – 2) = 0
⇒ 2x ( – 4) = 0
⇒ – 8 x = 0
Therefore, the zero of the polynomial = 0
Q.13. By actual division, find the quotient and the remainder when the first polynomial is divided by the second polynomial : x4 + 1; x –1
Performing the long division method, we get,
Hence, from the above long division method, we get, Quotient = x3 + x2 + x + 1
Remainder = 2.
Q.14. By Remainder Theorem find the remainder, when p(x) is divided by g(x), where
(i) p(x) = x3 – 2x2 – 4 x – 1, g(x) = x + 1
Let g(x) = x + 1
x + 1 = 0
x = –1
p(x) = x3 – 2x2 – 4x – 1
p(–1) = (–1)3 – 2(– 1)2 – 4(–1) – 1
= –1 – 2 × 1 + 4 – 1
= – 4 – 4 = 0
∴ Remainder = 0.
(ii) p(x) = x3 – 3x2 + 4 x + 50, g(x) = x – 3
p(x) = x3 – 3x2 + 4x + 50, g(x) = x – 3
Let g(x) = x – 3
x – 3 = 0
x = 3
p(3) = 33 – 3(32) + 4(3) + 50
= 27 – 27 + 12 + 50
= 62
∴ Remainder = 62.
(iii) p(x) = 4x3 – 12x2 + 14x – 3, g (x) = 2x – 1
Let us denote the given polynomials as
p(x) = 4x2 - 12x3 - 12x2 + 14x - 3,
g(x) = 2x - 1
⇒ g(x) =
We have to find the remainder when f(x) is divided by g(x).
By the remainder theorem, when f(x) is divided by g(x) the remainder is
= 1/2 - 3 + 7 - 3
= 3/2
Now we will calculate the remainder by actual division
So the remainder by actual division is 3/2 .
(iv) p(x) = x3 – 6x2 + 2x – 4, g(x) = 1 – 3/2 x
Given, p(x) = x3 – 6x2 + 2x – 4 and g(x) = 1 - 3/2x
Here, zero of g(x) is 2/3.
When we divide p(x) by g(x) using remainder theorem, we get the remainder p (2/3).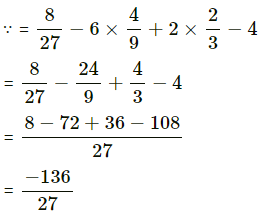
Hence, remainder is -136/27
Q.15. Check whether p(x) is a multiple of g(x) or not:
(i) p(x) = x3 – 5x2 + 4 x – 3, g(x) = x – 2
According to the question, g(x) = x – 2,
Then, zero of g(x), g(x) = 0
x – 2 = 0
x = 2
Therefore, zero of g(x) = 2
So, substituting the value of x in p(x), we get, p(2) =(2)3 – 5(2)2 + 4(2) – 3
= 8 – 20 + 8 – 3
= – 7 ≠ 0
Hence, p(x) is not the multiple of g(x) since the remainder ≠ 0.
(ii) p(x) = 2x3 – 11x2 – 4 x + 5, g (x) = 2x + 1
According to the question, g(x)= 2𝑥 + 1
Then, zero of g(x), g(x) = 0
2x + 1 = 0
2x = – 1
x = –1/2
Therefore, zero of g(x) = – 1/2
So, substituting the value of x in p(x), we get,
p(–1/2) = 2 × ( – 1/2 )3 – 11 × ( – 1/2 )2 – 4 × ( – 1/2) + 5
= – 1/4 - 11/4 + 7
= 16/4
= 4 ≠ 0
Hence, p(x) is not the multiple of g(x) since the remainder ≠ 0.
Q.16. Show that: (i) x + 3 is a factor of 69 + 11x – x2 + x3.
According to the question,
Let p(x) = 69 + 11x − x2 + x3 and
g(x) = x + 3 g(x) = x + 3
zero of g(x) ⇒ g(x) = 0 x + 3 = 0
x = – 3
Therefore, zero of g(x) = – 3
So, substituting the value of x in p(x),
we get, p( – 3) = 69 + 11(– 3) –(–3)2 + (– 3)3
= 69 – 69
= 0
Since, the remainder = zero, We can say that,
g(x) = x + 3 is factor of p(x) = 69 + 11x − x2 + x3
(ii) 2x – 3 is a factor of x + 2x3 – 9x2 + 12.
Let p(x) = 2x3 - 9x2 + x + 12
We have to show that, 2x - 3 is a factor of p(x).
= (81 – 81)/4
= 0
Hence, (2x – 3) is a factor of p(x).
Q.17. Determine which of the following polynomials has x – 2 a factor:
(i) 3x2 + 6x – 24
According to the question,
Let p(x) = 3𝑥2 + 6𝑥 − 24 and g(x) = x – 2 g(x) = x – 2
zero of g(x) ⇒ g(x) = 0 x – 2 = 0
x = 2
Therefore, zero of g(x) = 2
So, substituting the value of x in p(x), we get, p(2) = 3(2)2 + 6 (2) – 24
= 12 + 12 – 24
= 0
Since, the remainder = zero, We can say that,
g(x) = x – 2 is factor of p(x) = 3𝑥2 + 6𝑥 − 24
(ii) 4x2 + x – 2
According to the question,
Let p(x) = 4𝑥2 + 𝑥 − 2 and g(x) = x – 2 g(x) = x – 2
zero of g(x) ⇒ g(x) = 0 x – 2 = 0
x = 2
Therefore, zero of g(x) = 2
So, substituting the value of x in p(x), we get, p(2) = 4(2)2 + 2−2
= 16 ≠ 0
Since, the remainder = zero, We can say that,
g(x) = x – 2 is factor of p(x) = 4𝑥2 + 𝑥 − 2
Q.18. Show that p – 1 is a factor of p10 – 1 and also of p11 – 1.
Let f(p) = p10 – 1 and g(p) = p11 – 1
Putting p = 1 in f(p), we get
f(1) = 110 − 1 = 1 − 1 = 0
Therefore, by factor theorem, (p – 1) is a factor of (p10 – 1)
Now, putting p = 1 in g(p), we get
g(1) = 111 − 1 = 1 − 1 = 0
Therefore, by factor theorem, (p – 1) is a factor of (p11 – 1)
Q.19. For what value of m is x3 – 2mx2 + 16 divisible by x + 2 ?
According to the question,
Let p(x) = x3 – 2mx2 + 16, and g(x) = x + 2 g(x) = 0
⟹ x + 2 = 0
⟹ x = – 2
Therefore, zero of g(x) = – 2 We know that,
According to factor theorem,
if p(x) is divisible by g(x), then the remainder p(−2) should be zero. So, substituting the value of x in p(x), we get,
p( – 2) = 0
⟹ ( – 2)3 – 2m( – 2)2 + 16 = 0
⟹ 0 – 8 – 8m + 16 = 0
⟹ 8m = 8
⟹ m = 1
Q.20. If x + 2α is a factor of x5 – 4 α2x3 + 2 x + 2α + 3, find α.
According to the question,
Let p(x) = x5 – 4a2x3 + 2x + 2a + 3 and g(x) = x + 2a g(x) = 0
⟹ x + 2a = 0
⟹ x = – 2a
Therefore, zero of g(x) = – 2a We know that,
According to the factor theorem,
If g(x) is a factor of p(x), then p( – 2a) = 0 So, substituting the value of x in p(x), we get,
p ( – 2a) = (– 2a)5 – 4a2(– 2a)3 + 2(– 2a) + 2a + 3 = 0
⟹ – 32a5 + 32a5 – 2a + 3 = 0
⟹ – 2a = – 3
⟹ a = 3/2
Q.21. Find the value of m so that 2x – 1 be a factor of 8x4 + 4x3 – 16x2 + 10x + m.
Let p(x) = 8x4 + 4x3 – 16x2 + 10x + m
Since, 2x - 1 is a factor of p(x), then put p(1/2) = 0
⇒ 1 + 1 + m = 0
∴ m = – 2
Hence, the value of m is – 2.
Q.22. If x + 1 is a factor of ax3 + x2 – 2 x + 4 a – 9, find the value of a.
Let p(x) = ax3 + x2 – 2x + 4a – 9
Since, x + 1 is a factor of p(x), then put p(– 1) = 0
∴ a(-1)3 + (-1)2 - 2(-1) + 4a - 9 = 0
⇒ -a + 1 + 2 + 4a - 9 = 0
⇒ 3a - 6 = 0
⇒ 3a = 6
⇒ a = 6/3 = 2
Hence, the value of a is 2.
Q.23. Factorise:
(i) x2 + 9 x + 18
x2 + 9x + 18 = x2 + 3x + 6x + 18
= x(x + 3) + 6(x + 3)
= (x + 3)(x + 6)
(ii) 6x2 + 7 x – 3
6x2 + 7x − 3 = 6x2 + 9x − 2x − 3
= 3x(2x + 3) − 1(2x+3)
= (3x − 1)(2x + 3)
(iii) 2x2 – 7 x – 15
2x2 − 7x − 15 = 2x2 − 10x + 3x − 15
= 2x(x − 5) + 3(x − 5)
= (x − 5)(2x + 3)
(iv) 84 – 2r – 2 r2
84 − 2r − 2r2 = −(2r2 + 2r − 84)
= −(2r2 + 14r + 12r − 84)
= −(2r(r + 7) − 12(r + 7))
= −(r + 7)(2r − 12)
Q.24. Factorise:
(i) 2x3 – 3x2 – 17x + 30
2x3 − 3x2 − 17x + 30
= 2x3 + 2x2 − 12x − 5x2 − 5x + 30
= 2x(x2 + x − 6) − 5(x2 + x - 6)
= (x2 + x−6)(2x − 5)
= (x2 + 3x − 2x − 6)(2x − 5)
= [x(x + 3) − 2(x + 3)](2x − 5)
= (x + 3)(x − 2)(2x − 5)
(ii) x3 – 6x2 + 11x – 6
Let p(x) = x3 - 6x2 + 11x - 6
By trial, we find that
p(1) = (1)3 - 6(1)2 + 11(1) - 6 = 0
∴ By converse of factor theorem, (x - 1) is a factor of p(x).
Now, x3 - 6x2 + 11x - 6
= x2 (x - 1)- 5x (x - 1) + 6 (x - 1)
= (x - 1) (x2 - 5x + 6)
= (x - 1) {x2 - 2x - 3x + 6}
= (x - 1) {x(x - 2)-3 (x - 2)}
= (x - 1)(x - 2)(x - 3)
(iii) x3 + x2 – 4x – 4
Let x + 1 = 0
∴ x = -1
On substituting value of x in the expression
∴ f(-1) = (-1)3 + (-1)2 - 4(-1) -4 = 0
Clearly x + 1 is a factor of
f(x) = x3 + x2 - 4x - 4
∴ f(x) = (x + 1) (x2 - 4) ...(By actual division)
= (x + 1) (x - 2) (x + 2)
(iv) 3x3 – x2 – 3x + 1
Let f(x) = 3x3 - x2 - 3x + 1 be the given polynomial.
Now, putting x = 1, we get
f(1) = 3(1)3 - (1)2 - 3(1) + 1
= 3 - 1 - 3 + 1 = 0
Therefore, (x-1) is a factor of polynomial f(x).
Now,
f(x) = 3x2(x-1) + 2x(x-1) - 1(x - 1)
= (x - 1){3x2 + 2x - 1}
= (x - 1){3x2 + 2x - 1}
= (x - 1)(x + 1)(3x - 1)
Hence (x - 1), (x + 1) and (3x - 1 )are the factors of polynomial f(x).
Q.25. Using suitable identity, evaluate the following:
(i) 1033
= (100 + 3)3
= (100)3 + (3)3 + 3 x 100 x 3 x (100 + 3)
= 1000000 + 27 + 900 (103)
= 1000027 + 92700
= 1092727
(ii) 101 × 102
= (100 + 1) (100 + 2)
= (100) + 100(1 + 2) + 1 x 2
= 10000 + 300 + 2
= 10302
(iii) 9992
= (1000 - 1)2
= (1000)2 + (1)2 - 2 x 1000 x 1
= 1000000 + 1 - 2000
= 998001
Q.26. Factorise the following:
(i) 4x2 + 20x + 25
4x2 + 20x + 25 = (2x)2 + 2 × 2x × 5 + (5)2
= (2x+5)2 ........[Using identity, a2 + 2ab + b2 = (a + b)2]
(ii) 9y2 – 66yz + 121z2
Using (a−b)2 = a2 + b2 −2ab
= (3y)2 + (11z)2 −2 × 3y × 11
= (3y−11z)2
(iii) 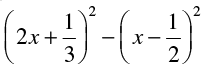
Using a2 − b2 = (a+b) (a−b)
Q.27. Factorise the following:
(i) 9x2 – 12x + 3
⇒ 9x2 − 3x − 9x + 3
⇒ 3x(3x − 1) − 3(3x −1)
⇒ (3x − 3)(3x − 1)
⇒ 3(x − 1)(3x − 1)
(ii) 9x2 – 12x + 4
9x2 – 12x + 4 = (3x)2 - 2 × 3x × 2 + (2)2
= (3x-2)2 .....[Using identity, (a – b)2 = a2 – 2ab + b2]
= (3x-2) (3x-2)
Q.28. Expand the following :
(i) (4a – b + 2 c)2
We have,
(4a − b + 2c)2
=(4a)2 +(−b)2 +(2c)2 + 2(4a)(−b) + 2(−b)(2c) + 2(2c)(4a)
[∵ a2 + b2 + c2 + 2ab + 2bc + 2ca = (a + b + c)2]
=16a2 + b2 + 4c2 −8ab − 4ac + 16ca
(ii) (3a – 5b – c)2
(3a − 5b − c)2
= (3a)2 + (−5b)2 + (−c)2 + 2(3a)2 − 5b+2(−5b)(−c) + 2(−c)(3a)
[∵ a2 + b2 + c2 + 2ab + 2bc + 2ca = (a + b + c)2]
= 9a2 + 25b2 + c2 − 30ab + 10bc − 6ca.
(iii) (– x + 2y – 3z)2
We know that,
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
Substituting, a = x, b = 2y and c = 3z
(x + 2y + 3z)2 = x2 + (2y)2 + (3z)2 + 2(x)(2y) + 2(2y)(3z) + 2(3z)(x)
= x2 + 4y2 + 9z2 + 4xy + 12y2 + 6zx
Q.29. Factorise the following :
(i) 9x2 + 4 y2 + 16z2 + 12xy – 16yz – 24xz
= (3x)2 + (2y)2 + (−4z)2 + 2(3x)(2y) + 2(2y)(−4z) + 2(−4z)(3x)
= (3x + 2y−4z)2= (3x + 2y − 4z)(3x + 2y − 4z)
(ii) 25x2 + 16y2 + 4z2 – 40xy + 16yz – 20xz
25x2 +16y2 +4z2 −40xy + 16yz − 20xz
= (−5x)2 +(4y)2 +(2z)2 + 2(−5x)(4y) + 2(4y)(2z) + 2(−5x)(2z)
Suitable identities is (x + y + z)3 = x3 + y3 + z3 + 2xy + 2yz + 2xz
Therefore, (−5x)2 +(4y)2 +(2z)2 + 2(−5x)(4y) + 2(4y)(2z) + 2(−5x)(2z)
= (−5x + 4y + 2z)2
(iii) 16x2 + 4y2 + 9z2 – 16xy – 12yz + 24 xz
16x2 + 4y2 + 9z2 −16xy −12yz + 24xz
Using identity,(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
16x2 + 4y2 + 9z2 − 16xy − 12yz + 24xz
=(4x)2 + (−2y)2 + (3z)2 + 2(4x)(−2y) + 2(−2y)(3z) + 2(3z)(4x)
=(4x − 2y + 3z)2
Q.30. If a + b + c = 9 and ab + bc + ca = 26, find a2 + b2 + c2.
Given, a + b + c = 9 and ab + bc + ca = 26.
We know, (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
⇒(a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca).
Putting the values here, we get,
(9)2 = a2 + b2 + c2 + 2(26)
⇒ 81 = a2 + b2 + c2 + 52
⇒ a2 + b2 + c2 = 81 − 52 = 29.
Hence, option D is correct.
Q.31. Expand the following :
(i) (3a – 2b)3
= (3a)3 – (2b)3 – 3(3a)(2b) [3a – 2b]
= 27a3 – 8b3 – 18ab (3a – 2b)
= 27a3 – 8b3 – 54a2b + 36ab2
= 27a3 – 54a2b + 36ab2 – 8b3
(ii) (1/x + y/3)3
......[Using identity, (a + b)3 = a3 + b3 + 3ab(a + b)]
Q.32. Factorise the following
(i) 1 – 64a3 – 12a + 48a2
= (1)3 −(4a)3 − 3(1)2 (4a) + 3(1)(4a)2
Suitable identities is x3 − y3 - 3x2 y + 3xy2 = (x−y) 3
∴(1)3 −(4a)3 −3(1)2 (4a) + 3(1)(4a)2
= (1−4a)3
(ii) 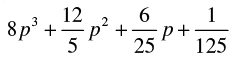
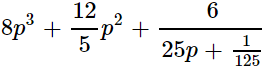
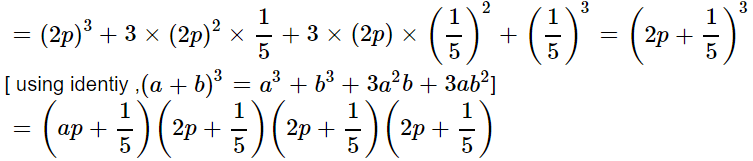
Q.33. Find the following products :
(i) 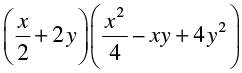
= (x/2)3 + (2y)3 [(a + b)(a2 − ab + b2) = a3 + b3]
= x3/8 + 8y3
(ii) (x2 – 1) (x4 + x2 + 1)
Given (x2 - 1) (x4 + x2 + 1)
We shall use the identity (a - b) (a2 + ab + b2) = a3 - b3
We can rearrange the (x2 - 1) (x4 + x2 + 1) as
(x2 − 1) [(x2)2 + (x2) (1) + (1)2]
=(x2)3 - (1)3
=(x2) × (x2) × (x2) - (1) × (1) × (1)
= x6 - 13
= x6 - 1
Hence the Product value of (x2 - 1)(x4 + x2 + 1) is x6 - 1.
Q.34. Factorise :
(i) 1 + 64x3
We know, (a3 + b3) = a3 + a2b − a2b − ab2 + ab2 + b3
= (a3 + a2b) − (a2b + ab2) + (ab2 + b3)
= a2(a + b) − ab(a + b) + b2(a + b)
= (a + b)(a2 − ab + b2)
Now, given, 1 + 64x3
=13 + (4x)3
= (1 + 4x)(1 − 4x(1) + (4x2))
= (1 + 4x)(1 − 4x + 16x2)
(ii) a3 –2√2b3
(a3 - b3) = a3 - a2b + a2b − ab2 + ab2 - b3
= (a3 - a2b) + (a2b - ab2) + (ab2 - b3)
= a2(a - b) + ab(a - b) + b2(a - b)
= (a - b)(a2 + ab + b2)
Now, given a3 − 2√2b3
=(a − √2b)(a2 + a(√2b) + (√2b)2)
= (a − √2b)(a2 + √2ab + 2b2)
Q.35. Find the following product: (2x – y + 3z) (4x2 + y2 + 9z2 + 2xy + 3yz – 6xz)
= (2x − y + 3z)(4x2 + y2 + 9z2 + 2xy + 3yz − 6xz)
= (a + b + c)(a2 + b2 + c2 - ab − bc − ac)
= a3 + b3 + c3−3abc
= (2x)3 + (−y)3 + (3z)3 − 3.(2x)(−y)(3z)
= 8x3 − y3 + 27z3 + 18xyz
Q.36. Factorise :
(i) a3 – 8b3 – 64c3 – 24abc
Here the given expression can be written as,
a3 − 8b3 − 64c3 −24abc = (a)3 + (−2b)3 + (−4c)3 −3(a)(−2b)(−4c)
Comparing with the given identity,
x3 + y3 + z3 −3xyz ≡ (x + y + z)(x2 + y2 + z2 − xy − yz − xz)
We get factor as
= (a − 2b − 4c)[(a)2 − (−2b)2 + (−4c)2 − (a)(−2b) − (−2b)(−4c) − (−4c)(a)]
= (a − 2b − 4c)(a2 + 4b2 + 16c2 + 2ab − 8bc + 4ca)
(ii) 2√2a3 + 8b3 – 27c3 + 18√2 abc.
We know that,
a3 + b3 + c3 −3abc = (a + b + c)(a2 + b2 + c2 − ab − bc − ca)
Thus, 2√2a3 + 8b3 − 27c3 + 18√2 abc
Here, a = √2 a, b = 2b and c = −3c
= (√2a + 2b − 3c)[(√2a)2 + (2b)2 + (−3c)2 − √2a(2b) − (2b)(−3c)−(−3c)(√2a)]
= (√2a + 2b − 3c)(2a2 + 4b2 + 9c2 − 2√2ab + 6bc + 3√2ac)
Q.37. Without actually calculating the cubes, find the value of :
(i) 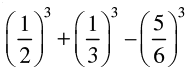
Let
We know that a3 + b3 + c3 = 3abc when a + b + c = 0
= - 5/12
(ii) (0.2)3 – (0.3)3 + (0.1)3
Given,
0.23 − 0.33 + 0.13= (0.1 × 2)3 − (0.1 × 3)3 + (0.1 × 1)3
= 0.13(23 − 33 + 13)
= 0.13(−18) = −0.018
Q.38. Without finding the cubes, factorise
(x – 2y)3 + (2y – 3z)3 + (3z – x)3
We know that, a3 + b3 + c3 − 3abc = (a + b + c) (a2 + b2 + c2 − ab − bc − ca)
Also, if a + b + c = 0,
then a3 + b3 + c3 = 3abc .....condition(1)
Here, we see that a + b + c = (x − 2y) + (2y − 3z) + (3z − x) = 0∴ Using condition (1), we get
⇒ (x − 2y)3 + (2y − 3z)3 + (3 z − x)3
= 3(x − 2y) (2y − 3z) (3z − x)
Q.39. Find the value of
(i) x3 + y3 – 12xy + 64, when x + y = – 4
We know that, a3 + b3 + c3 = (a + b + c) (a2 + b2 + c2 − ab − bc − ca) + 3abc
If a + b + c = 0, then a3 + b3 + c3 = 3abc
Now, given x3 + y3 −12xy + 64 and
x + y = −4
=> x + y + 4 = 0
Here, a = x, b = y, c = 4 and a + b + c = x + y + 4 = 0
Therefore x3 + y3 + 64 = 3xy(4)
= 12xyz
Now, x3 + y3 + 64 − 12xyz = 12xyz − 12xyz = 0
(ii) x3 – 8y3 – 36xy – 216, when x = 2y + 6
x3 − 8y3 − 36xy − 216
= x3 + (−2y)3 + (−6)3 − 3(x)(−2y)(−6)
= (x−2y−6)(x2 + 4y2 + 36 + 2xy − 12y + 6x)
= 0 × (x2 + 4y2 + 36 + 2xy − 12y + 6x) = 0
Q.40. Give possible expressions for the length and breadth of the rectangle whose area is given by 4a2 + 4a –3.
Given
Area = 4a2 + 4a − 3.
We know that
Area of rectangle = length × breadth
So, to find the possible expressions for the length and breadth we have to factorise the given expression.
Using the method of splitting the middle term,4a + 4a−3
= 4a2 + 6a − 2a − 3
= 2a(2a+3)−1(2a+3)
= (2a−1)(2a+3)
∴ length × breadth =(2a−1)(2a+3)
Hence, the possible expressions for the length and breadth of the rectangle are :
length = (2a−1) and breadth =(2a+3) or, length = (2a + 3) and breadth = (2a − 1).
Exercise 2.4
Q1. If the polynomials az3 + 4 z2 + 3 z – 4 and z3 – 4 z + a leave the same remainder when divided by z – 3, find the value of a.
Solution: Let p1(z) = az3 + 4z2 + 3z – 4 and p2(z) = z3 – 4z + 0
When we divide p1(z) by z – 3, then we get the remainder p,(3).
Now, p1(3) = a(3)3 + 4(3)2 + 3(3) – 4
= 27a + 36 + 9 – 4
= 27a + 41
When we divide p2(z) by z – 3 then
we get the remainder p2(3).
Now, p2(3) = (3)3 – 4(3) + a
= 27 – 12 + a
= 15 + a
Both the remainders are same.
p1(3) = p2(3)
27a + 41 = 15 + a
27a – a = 15 – 41 .
26a = 26a = – 1
Q2. The polynomial p(x) = x4 – 2x3 + 3x2 – ax + 3a – 7 when divided by x + 1 leaves the remainder 19. Find the values of a. Also find the remainder when p(x) is divided by x + 2.
Solution: Given, p(x) = x4 – 2x3 + 3x2 – ax + 3a – 7
When we divide p(x) by x + 1, then we get the remainder p(– 1).
Now, p(– 1) = (– 1)4 – 2(– 1)3 + 3(– 1)2 – a(– 1) + 3a – 7
= 1 + 2 + 3 + a + 3a – 7
= 4a – 1
p(– 1) = 19
⇒ 4a – 1 = 19
⇒ 4a = 20
∴ a = 5
∴ Required polynomial = x4 – 2x3 + 3x2 – 5x + 3(5) – 7 .....[Put a = 5 on p(x)]
= x4 – 2x3 + 3x2 – 5x + 15 – 7
= x4 – 2x3 + 3x2 – 5x + 8
When we divide p(x) by x + 2, then we get the remainder p(– 2)
Now, p(– 2) = (– 2)4 – 2(– 2)3 + 3(– 2)2 – 5(– 2) + 8
= 16 + 16 + 12 + 10 + 8
= 62
Hence, the value of a 5 and remainder is 62.
Q3. If both x – 2 and x – 1/2 are factors of px2 + 5x + r, show that p = r.
Solution: As (x - 2)and (x - 1/2)are the factors of the polynomial px2 + 5x + r
i.e., f(2) = 0 and f(1/2) = 0
Now,
f(2) = p(2)2 + 5(2) + r = 0
4p + r = -10 .....(1)
And
p/4 + 5/2 + r = 0
p + 10 + 4x = 0p + 4x = -10 ........(2)
From equation (1) and (2), we get
4p + r = p + 4r
3p = 3x
p = r
Q4. Without actual division, prove that 2x4 – 5x3 + 2x2 – x + 2 is divisible by x2 – 3x + 2.
Solution: Let p(x) = 2x4 – 5x3 + 2x2 – x + 2 firstly, factorise x2 - 3x + 2.
Now, x2 - 3x + 2 = x2 - 2x - x + 2 [by splitting middle term]
= x(x-2)-1 (x-2)
= (x-1)(x-2)
Hence, 0 of x2 - 3x + 2 are land 2.
We have to prove that, 2x4 – 5x3 + 2x2 – x + 2 is divisible by x2 - 3x + 2 i.e., to prove that p (1) =0 and p(2) =0
Now, p(1) = 2(1)4 – 5(1)3 + 2(1)2 -1 + 2
= 2 - 5 + 2 - 1 + 2
= 6 - 6
= 0
and p(2) = 2(2)4 – 5(2)3 + 2(2)2 – 2 + 2
= 2x16 - 5x8 + 2x4 + 0
= 32 – 40 + 8
= 40 – 40
= 0
Hence, p(x) is divisible by x2 - 3x + 2.
Q5. Simplify (2x – 5y)3 – (2x + 5y)3.
Solution: (2x -5y)3 – (2x + 5y)3
= [(2x)3 – (5y)3 – 3(2x)(5y)(2x – 5y)] -[(2x)3 + (5y)3 + 3(2x)(5y)(2x+5y)]
[using identity, (a – b)3 = a3 -b3 – 3ab and (a + b)3 = a3 +b3 + 3ab]
= (2x)3 – (5y)3 – 30xy(2x – 5y) – (2x)3 – (5y)3 – 30xy (2x + 5y)
= -2 (5y)3 – 30xy(2x – 5y + 2x + 5y)
= -2 x 125y3 – 30xy(4x)
= -250y3 -120x2y
Q6. Multiply x2 + 4y2 + z2 + 2xy + xz – 2yz by (– z + x – 2 y).
Solution: (x–2y–z)(x2 + 4y2 + z2 + 2xy + xz − 2yz)
= (x − 2y − z)[(x)2 + (−2y)2 + (−z)2 − (x)(−2y) − (−2y)(−z) − (x)(−z)]
= (x)3 + (−2y)3 +(−z)3 – 3(x)(−2y)(−z)
[Using the identity, a3 + b3 + c3 − 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ca)]
= x3 – 8y3 – z3 – 6xyz
Q7. If a, b, c are all non-zero and a + b + c = 0, prove that 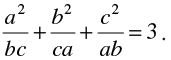
Solution: To prove,
We know that, a3 + b3 + c3 – 3abc = (a + b + c) (a2 + b2 + c2 – ab – bc – ca)
= 0(a2 + b2 + c2 – ab – bc – ca) [∵ a + b + c = 0 , given]
= 0
→ a3 + b3 + c3 = 3 abc
On dividing both sides by abc; we get,
Q8. If a + b + c = 5 and ab + bc + ca = 10, then prove that a3 + b3 + c3 –3abc = – 25.
Solution: Given: a + b + c = 5 and ab + bc + ca = 10
We know that: a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ca)
= (a + b + c)[a2 + b2 + c2 – (ab + bc + ca)]
= 5{a2 + b2 + c2 – (ab + bc + ca)} = 5(a2 + b2 + c2 – 10)
Given: a + b + c = 5
Now, squaring both sides, get: (a + b + c)2 = 52
a2 + b2 + c2 + 2(ab + bc + ca)
= 25 a2 + b2 + c2 + 2 × 10
= 25 a2 + b2 + c2 = 25 – 20
= 5
Now, a3 + b3 + c3 – 3abc = 5(a2 + b2 + c2 – 10)
= 5 × (5 – 10)
= 5 × (– 5)
= – 25Hence proved.
Q9. Prove that (a + b + c)3 – a3 – b3 – c3 = 3(a + b ) ( b + c) (c + a).
Solution: To prove: (a + b + c)3 – a3 – b3 – c3 = 3(a + b)(b + c)(c + a)
L.H.S = [(a + b + c)3 – a3] – (b3 + c3)
= (a + b + c – a)[(a + b + c)2 + a2 + a(a + b + c)] – [(b + c)(b2 + c2 – bc)] .......[Using identity, a3 + b3 = (a + b)(a2 + b2 – ab) and a3 – b3 = (a – b)(a2 + b2 + ab)]
= (b + c)[a2 + b2 + c2 + 2ab + 2bc + 2ca + a2 + a2 + ab + ac] – (b + c)(b2 + c2 – bc)
= (b + c)[b2 + c2 + 3a2 + 3ab + 3ac – b2 – c2 + 3bc]
= (b + c)[3(a2 + ab + ac + bc)]
= 3(b + c)[a(a + b) + c(a + b)]
= 3(b + c)[(a + c)(a + b)]
= 3(a + b)(b + c)(c + a) = R.H.S
Hence proved.
|
40 videos|471 docs|57 tests
|
FAQs on NCERT Exemplar Solutions: Polynomials - Mathematics (Maths) Class 9
| 1. What are polynomials in mathematics? |  |
| 2. How do you classify polynomials based on the number of terms they have? |  |
| 3. What is the degree of a polynomial and how is it determined? |  |
| 4. How can you add or subtract polynomials? |  |
| 5. Can you factorize polynomials and if so, how? |  |