NCERT Exemplar Solutions: Ratio & Proportion | Mathematics for Class 6 PDF Download
Exercise Page: 120
In questions 1 to 10, only one of the four options is correct. Write the correct one.
Q1: The ratio of 8 books to 20 books is
(a) 2 : 5
(b) 5 : 2
(c) 4 : 5
(d) 5 : 4
 View Answer
View Answer 
Ans: (a)
The comparison of two numbers or quantities by division is known as the ratio. Symbol ‘:’ is used to denote ratio.
Ratio of 8 books to 20 books = 8/20
Divide both numerator and denominator by 4.
= 2/5
Therefore, ratio of 8 books to 20 books = 2 : 5
Q2: The ratio of the number of sides of a square to the number of edges of a cube is
(a) 1 : 2
(b) 3 : 2
(c) 4 : 1
(d) 1 : 3
 View Answer
View Answer 
Ans: (d)
We know that, number of sides in a square = 4 and number of edges in a cube = 12
So, ratio of sides to edges = 4/12
Divide both numerator and denominator by 4.
= 1/3
Therefore, ratio of sides to edges = 1 : 3
Q3: A picture is 60cm wide and 1.8m long. The ratio of its width to its perimeter in lowest form is
(a) 1 : 2
(b) 1 : 3
(c) 1 : 4
(d) 1 : 8
 View Answer
View Answer 
Ans: (d)
From the question it is given that,
Width of a picture = 60 cm
Length of a picture = 1.8 m
We know that, 1 m = 100 cm
So, 1.8 m = 180 cm
Perimeter of rectangle = 2 (length + breadth)
= 2 (180 + 60)
= 2 (240)
= 480
Therefore, The ratio of its width to its perimeter in lowest form = 60/480
Divide both numerator and denominator by 20.
= 3/24
Again, divide both numerator and denominator by 3.
= 1/8
= 1 : 8
Q4: Neelam’s annual income is Rs. 288000. Her annual savings amount to Rs. 36000. The ratio of her savings to her expenditure is
(a) 1 : 8
(b) 1 : 7
(c) 1 : 6
(d) 1 : 5
 View Answer
View Answer 
Ans: (b)
From the question it is given that,
Neelam’s annual income is ₹ 288000
Her annual savings amount to ₹ 36000
So, Neelam’s expenditure = 288000 – 36000
= ₹ 252000
Then, ratio of her savings to her expenditure = 36000/252000
= 36/252
Divide both numerator and denominator by 12.
= 3/21
Again, divide both numerator and denominator by 3.
= 1/7
Therefore, ratio of her savings to her expenditure = 1 : 7
Q5: Mathematics textbook for Class VI has 320 pages. The chapter ‘symmetry’ runs from page 261 to page 272. The ratio of the number of pages of this chapter to the total number of pages of the book is
(a) 11 : 320
(b) 3 : 40
(c) 3 : 80
(d) 272 : 320
 View Answer
View Answer 
Ans: (c)
From the question it is given that,
Total number of pages in the Mathematics textbook for Class VI = 320 pages
The chapter ‘symmetry’ runs from page 261 to page 272
Number of pages contains symmetry chapter = 12
So, the ratio of the number of pages of symmetry chapter to the total number of pages of the book is,
= 12/320
Divide both numerator and denominator by 2.
= 6/160
Again, divide both numerator and denominator by 2.
= 3/80
Therefore, the ratio of the number of pages of this chapter to the total number of pages of the book is 3: 80.
Q6: In a box, the ratio of red marbles to blue marbles is 7:4. Which of the following could be the total number of marbles in the box?
(a) 18
(b) 19
(c) 21
(d) 22
 View Answer
View Answer 
Ans: (d)
From the question it is given that, the ratio of red marbles to blue marbles is 7:4.
Now, let us assume the common factor of 7 and 4 be x.
So, the total number of marbles in the box = 7x + 4x = 11x
Hence number of marbles in the box is a multiple of 11.
Therefore, 11 × 2 = 22
Q7: On a shelf, books with green cover and that with brown cover are in the ratio 2 : 3. If there are 18 books with green cover, then the number of books with brown cover is
(a) 12
(b) 24
(c) 27
(d) 36
 View Answer
View Answer 
Ans: (c)
From the question it is given that,
On a shelf, books with green cover and that with brown cover are in the ratio 2:3
There are 18 books with green cover
So, let us assume the common factor of 2 and 3 be x.
Then, 2x = 18
x = 18/2
Divide both numerator and denominator by 2.
x = 9
Therefore, the number of books with brown cover is = 3x = 3 × 9
= 27
Q8: The greatest ratio among the ratios 2 : 3, 5 : 8, 75 : 121 and 40 : 25 is
(a) 2 : 3
(b) 5 : 8
(c) 75 : 121
(d) 40 : 25
 View Answer
View Answer 
Ans: (d)
Consider the given ratios, 2 : 3, 5 : 8, 75 : 121 and 40 : 25.
Simplified form of 2: 3 = 2/3 = 0.67
Simplified form of 5 : 8 = 5/8 = 0.625
Simplified form of 75: 121 = 75/121 = 0.61
Simplified form of 40: 25 = 40/25 = 1.6
Therefore, the greatest ratio among the given ratios is 40 : 25
Q9: There are ‘b’ boys and ‘g’ girls in a class. The ratio of the number of boys to the total number of students in the class is:
(a) b/(b + g)
(b) g/(b + g)
(c) b/g
(d) (b + g)/b
 View Answer
View Answer 
Ans: (a)
From the question,
Number of boys in the class = b
Number of girls in the class = g
Total number of students in the class = b + g
Therefore, the ratio of the number of boys to the total number of students in the class
= b/(b + g)
Q10: If a bus travels 160 km in 4 hours and a train travels 320km in 5 hours at uniform speeds, then the ratio of the distances travelled by them in one hour is
(a) 1 : 2
(b) 4 : 5
(c) 5 : 8
(d) 8 : 5
 View Answer
View Answer 
Ans: (c)
From the question it is given that,
Bus travels 160 km in 4 hours
Train travels 320 km in 5 hours
So, distance travelled by bus in an hour = 160/4 = 40 km/h
Distance travelled by train in an hour = 320/5 = 64 km/h
Then the ratio of the distances travelled by them in one hour is = 40/64
Divide both numerator and denominator by 8.
= 5/8
Therefore, the ratio of the distances travelled by them in one hour is 5: 8.
In questions 11 to 15, find the missing number in the box [ ] in each of the proportions:
Q11: 3/5 = [ ]/20
 View Answer
View Answer 
Let us assume the missing number be y.
Then, (3/5) = (y/20)
By cross multiplication we get,
(3 × 20)/5 = y
y = 60/5
Divide both numerator and denominator by 5.
y = 12
Therefore, 3/5 = [12]/20
Q12: [ ]/18 = 2/9
 View Answer
View Answer 
Let us assume the missing number be y.
Then, y/18 = 2/9
By cross multiplication we get,
y = (2 × 18)/9
y = 36/9
Divide both numerator and denominator by 9.
y = 4
Therefore, [4]/18 = 2/9
Q13: 8/[ ] = 3.2/4
 View Answer
View Answer 
Let us assume the missing number be y.
Then, 8/y = 3.2/4
By cross multiplication we get,
y = (8 × 4)/3.2
y = 32/3.2
y = 320/32
Divide both numerator and denominator by 32.
y = 10
Therefore, 8/[10] = 3.2/4
Q14: [ ]/45 = 16/40 = 24/[ ]
 View Answer
View Answer 
Consider the first two ratios [ ]/45 = 16/40
Let us assume the missing number be P
Then, P/45 = 16/40
By cross multiplication we get,
P = (16 × 45)/40
P = 720/40
P = 72/4
Divide both numerator and denominator by 4.
P = 18
Therefore, [18]/45 = 16/40
Now, consider the last two ratios, 16/40 = 24/[ ]
Let us assume the missing number be Q,
Then, 16/40 = 24/Q
By cross multiplication we get,
Q = (24 × 40)/16
Q = 960/16
Divide both numerator and denominator by 16.
Q = 60
Therefore, 16/40 = 24/[60]
Q15: 16/36 = [ ]/63 = 36/[ ] = [ ]/117
 View Answer
View Answer 
Consider the first two ratios 16/36 = [ ]/63
Let us assume the missing number be P
Then, 16/36 = P/63
By cross multiplication we get,
P = (16 × 63)/36
P = 1008/36
Divide both numerator and denominator by 36.
P = 28
Therefore, 16/36 = [28]/63
Now, consider the middle two ratios, 28/63 = 36/[ ]
Let us assume the missing number be Q,
Then, 28/63 = 36/Q
By cross multiplication we get,
Q = (36 × 63)/28
Q = 2268/28
Divide both numerator and denominator by 28.
Q = 81
Therefore, 28/63 = 36/[81]
Consider the last two ratios 36/81 = [ ]/117
Let us assume the missing number be R
Then, 36/81 = R/117
By cross multiplication we get,
P = (36 × 117)/81
P = 4212/81
Divide both numerator and denominator by 81.
P = 52
Therefore, 36/81 = [52]/117
So, 16/36 = [28]/63 = 36/[81] = [52]/117
In questions 16 to 34, state whether the given statements are true (T) or false (F).
Q16: 3/8 = 15/40
 View Answer
View Answer 
True.
Consider the two fractions, 3/8 = 15/40
15/40 is further simplified by dividing both numerator and denominator by 5 we get,
= 3/8
Therefore, 3/8 = 3/8
Q17: 4 : 7 = 20 : 35
 View Answer
View Answer 
True.
Consider the two ratio, 4: 7 = 20: 35= 4/7 = 20/35
20/35 is further simplified by dividing both numerator and denominator by 5 we get,
= 4/7
Therefore, 4/7 = 4/7
Q18: 0.2 : 5 = 2 : 0.5
 View Answer
View Answer 
False.
Consider the two ratio, 0.2: 5 = 2: 0.50.2/5 = 2/0.5
0.04 ≠ 4
Q19: 3 : 33 = 33 : 333
 View Answer
View Answer 
False.
Consider the two ratios 3: 33 = 33 : 3333/33 = 33/333
0.0909 ≠ 0.0990
Q20: 15m : 40m = 35m : 65m
 View Answer
View Answer 
False.
Consider the two ratios 15m : 40m = 35m : 65m15/40 = 35/65
15/40 is further simplified by dividing both numerator and denominator by 5 we get,
= 3/8
35/65 is further simplified by dividing both numerator and denominator by 5 we get,
= 7/13
Hence, 3/8 ≠ 7/13
Therefore, 15/40 ≠ 35/65
Q21: 27cm2 : 57cm2 = 18cm : 38cm
 View Answer
View Answer 
True
Consider the two ratios 27cm2 : 57cm2 = 18cm : 38cm27/57 = 18/38
27/57 is further simplified by dividing both numerator and denominator by 3 we get,
= 9/19
18/38 is further simplified by dividing both numerator and denominator by 2 we get,
= 9/19
Hence, 9/19 = 9/19
Therefore, 27cm2 : 57cm2 = 18cm : 38cm
Q22: 5kg : 7.5kg = Rs 7.50 : Rs 5
 View Answer
View Answer 
False.
Consider the two ratios 5kg: 7.5kg = Rs 7.50: Rs 55/7.5 = 7.50/5
50/75 = 75/50
50/75 is further simplified by dividing both numerator and denominator by 25 we get,
= 2/3
75/50 is further simplified by dividing both numerator and denominator by 25 we get,
= 3/2
Hence, 2/3 ≠ 3/2
Therefore, 5kg: 7.5kg ≠ Rs 7.50: Rs 5
Q23: 20g : 100g = 1metre : 500cm
 View Answer
View Answer 
Consider the given ratios, 20g : 100g = 1metre : 500cm
20/100 = 1/500
We know that, 1 metre = 100 cm
So, 20g: 100g = 100cm : 500 cm
20/100 = 100/500
20/100 is further simplified by dividing both numerator and denominator by 20 we get,
= 1/5
100/500 is further simplified by dividing both numerator and denominator by 100 we get,
= 1/5
Hence, 1/5 = 1/5
Therefore, 20g : 100g = 1metre : 500cm
Q24: 12 hours : 30 hours = 8km : 20km
 View Answer
View Answer 
True
Consider the given ratios, 12 hours : 30 hours = 8km : 20km12/30 = 8/20
12/30 is further simplified by dividing both numerator and denominator by 6 we get,
= 2/5
8/20 is further simplified by dividing both numerator and denominator by 4 we get,
= 2/5
Hence, 2/5 = 2/5
Therefore, 12 hours : 30 hours = 8km : 20km
Q25: The ratio of 10kg to 100kg is 1:10
 View Answer
View Answer 
True.
The ratio of 10kg to 100kg = 10/100= 1/10
= 1:10
Q26: The ratio of 150cm to 1metre is 1:1.5.
 View Answer
View Answer 
False
We know that, 1 metre = 100 cmSo, the ratio of 150cm to 1metre is = 150/100
= 15/10
Divide both numerator and denominator by 5 we get,
= 3/2
So, the ratio of 150cm to 1metre is 3: 2
Q27: 25kg : 20g = 50kg : 40g
 View Answer
View Answer 
True.
We know that, 1 kg = 1000 gSo, 25 × 1000 = 25000 g
50 × 1000 = 50000g
Then, 25000g : 20g = 50000g : 40g
25000/20 = 50000/40
2500/2 = 5000/4
2500/2 is further simplified by dividing both numerator and denominator by 2 we get,
= 1250
5000/4 is further simplified by dividing both numerator and denominator by 4 we get,
= 1250
Hence, 1250 = 1250
So, 25kg : 20g = 50kg : 40g
Q28: The ratio of 1 hour to one day is 1:1.
 View Answer
View Answer 
We know that, 1 day = 24 hours
So, 1 hour: 1 day = 1 hour : 24 hours
1/1 ≠ 1/24
Q29: The ratio 4 :16 is in its lowest form.
 View Answer
View Answer 
False
4 : 16= 4/16
Divide both numerator and denominator by 4,
= 1/4
Therefore, lowest form of 4: 16 is 1/4
Q30: The ratio 5 : 4 is different from the ratio 4 : 5.
True.
 View Answer
View Answer 
5: 4 ≠ 4: 5
5/4 ≠ 4/5
1.25 ≠ 0.8
Q31: A ratio will always be more than 1.
 View Answer
View Answer 
False.
A ratio will be more than or less than 1Q32: A ratio can be equal to 1.
 View Answer
View Answer 
Example: 2: 2 = 2/2 = 1
Q33: If b : a = c : d, then a, b, c, d are in proportion.
 View Answer
View Answer 
False
Four quantities are said to be in proportion, if the ratio of the first and the second quantities is equal to the ratio of the third and the fourth quantities. The symbol ‘::’ or ‘=’ is used to equate the two ratios.Q34: The two terms of a ratio can be in two different units.
 View Answer
View Answer 
False.
For a ratio, the two quantities must be in the same unit. If they are not, they should be expressed in the same unit before the ratio is taken.In questions 35 to 46, fill in the blanks to make the statements true.
35: A ratio is a form of comparison by ______.
 View Answer
View Answer 
Q36: 20m : 70m = Rs 8 : Rs ______.
 View Answer
View Answer 
20m : 70m = Rs 8 : Rs 28.
Let us assume the missing number be P.
Then, 20m : 70m = ₹ 8 : ₹ P
20/70 = 8/P
P = (70 × 8)/20
P = 560/20
P = 56/2
P = 28
Therefore, 20m : 70m = Rs 8 : Rs 28.
Q37: There is a number in the box [ ] such that [ ], 24, 9, 12 are in proportion. The number in the box is _____.
 View Answer
View Answer 
There is a number in the box [ ] such that [ ], 24, 9, 12 are in proportion. The number in the box is 18.
Let us assume the missing number be ‘P’,
Then, P, 24, 9, 12
P: 24 = 9: 12
P/24 = 9/12
9/12 is further simplified by dividing both numerator and denominator by 3.
So, P/24 = 3/4
P = (3 × 24)/4
P = 72/4
P = 18
Therefore, the missing number is 18.
Q38: If two ratios are equal, then they are in _____.
 View Answer
View Answer 
If two ratios are equal, then they are in proportion.
Use Fig. (In which each square is of unit length) for questions 39 and 40:
Q39: The ratio of the perimeter of the boundary of the shaded portion to the perimeter of the whole figure is _______.
 View Answer
View Answer 
The ratio of the perimeter of the boundary of the shaded portion to the perimeter of the whole figure is 3: 7.
From the figure, perimeter of shaded portion = 1 + 2 + 1 + 2 = 6 units
Perimeter of whole figure = 3 + 4 + 3 + 4 = 14 units
Then, ratio of the perimeter of the boundary of the shaded portion to the perimeter of the whole figure = 6/14
= 3/7
= 3: 7
Q40: The ratio of the area of the shaded portion to that of the whole figure is ______.
 View Answer
View Answer 
The ratio of the area of the shaded portion to that of the whole figure is 1: 6.
Area of the shaded figure = 2 × 1
= 2 sq. units
Area of whole figure = 3 × 4 = 12 sq. units
The ratio of the area of the shaded portion to that of the whole figure is = 2: 12
= 2/12
= 1/6
= 1: 6
Q41: Sleeping time of a python in a 24 hour clock is represented by the shaded portion in Fig.
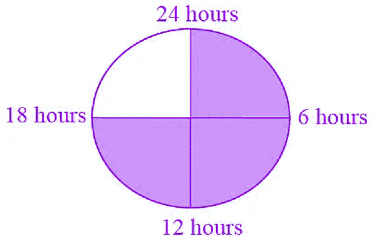 The ratio of sleeping time to awaking time is ______.
The ratio of sleeping time to awaking time is ______.
 View Answer
View Answer 
The ratio of sleeping time to awaking time is 3: 1.
From the figure, sleeping time = 18 hours
Then, awaking time = 24 – 18 = 6 hours
Therefore, the ratio of sleeping time to awaking time is 18/6
= 3/1
= 3: 1
Q42: A ratio expressed in lowest form has no common factor other than ______ in its terms.
 View Answer
View Answer 
A ratio expressed in lowest form has no common factor other than one in its terms.
Q43: To find the ratio of two quantities, they must be expressed in _____units.
 View Answer
View Answer 
To find the ratio of two quantities, they must be expressed in same units.
Q44: Ratio of 5 paise to 25 paise is the same as the ratio of 20 paise to _____
 View Answer
View Answer 
Ratio of 5 paise to 25 paise is the same as the ratio of 20 paise to 100 paise.
From the question,
5 paise : 25 paise = 20 paise: [ ]
Let us assume the missing number be Q,
5 paise : 25 paise = 20 paise: Q
5/25 = 20/Q
Q = (20 × 25)/5
Q = 500/5
Q = 100
Therefore, Ratio of 5 paise to 25 paise is the same as the ratio of 20 paise to 100 paise
Q45: Saturn and Jupiter take 9 hours 56 minutes and 10 hours 40 minutes, respectively for one spin on their axes. The ratio of the time taken by Saturn and Jupiter in lowest form is ______.
 View Answer
View Answer 
Saturn and Jupiter take 9 hours 56 minutes and 10 hours 40 minutes, respectively for one spin on their axes. The ratio of the time taken by Saturn and Jupiter in lowest form is 149: 160.
From the question,
Saturn takes 9 hours 56 minutes for one spin on their axes
We know that, 1 hour = 60 minutes
So, (9 × 60) + 56 = 540 + 56 = 596 minutes
Jupiter takes 10 hours 40 minutes for one spin on their axes
= (10 × 60) + 40
= 600 + 40
= 640 minutes
The ratio of the time taken by Saturn and Jupiter in lowest form is = 596/640
Divide both numerator and denominator by 2,
= 298/320
Again, divide both numerator and denominator by 2,
= 149/160
Therefore, the ratio of the time taken by Saturn and Jupiter in lowest form is 149 : 160.
Q46: 10 g of caustic soda dissolved in 100 mL of water makes a solution of caustic soda. Amount of caustic soda needed for 1 L of water to make the same type of solution is_________.
 View Answer
View Answer 
Given, 10 g of caustic soda dissolved in 100 mL water.
The ratio of caustic soda to water should be in proportion.
10g: 100 mL : :x g :1 L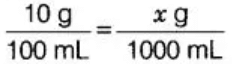 [∵ 1 L = 1000 mL]
[∵ 1 L = 1000 mL]
x g × 100 mL = 10 g × 1000 mL [by cross multiplication]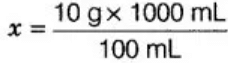
x = 100 g
Q47: The marked price of a table is Rs. 625 and its sale price is Rs. 500. What is the ratio of the sale price to the marked price?
 View Answer
View Answer 
Given, marked price of a table = ₹ 625
Sale price of a table = ₹ 500
Ratio of sale price to marked price = ₹500/625 = 500/625
= 20/25 [on dividing numerator and denominator by 25]
= 4/5 [on dividing numerator and denominator by 5]
∴ Required ratio = 4 : 5
Q48: Which pair of ratios are equal? And why?
(i) 2/3,4/6
(ii) 8/4,2/1
(iii) 4/5,12/20
 View Answer
View Answer 
(i) The given pair is equivalent as lowest form of 4/6 is 2/3 and other ratio is 2/3 .
(ii) The given pair is equivalent as lowest form of 8/4 is 2/1 and other ratio is —2/1
(iii) The given pair is not equivalent as lowest form of 12/20 is 3/5 and other ratio is 4/5 .
Q49: Which ratio is larger 10: 21 or 21: 93?
 View Answer
View Answer 
Ratio 10:21 is larger as it approximates to 0.476 and 21:93 approximates to 0.225.
Q50: Reshma prepared 18 kg of Burfi by mixing Khoya with sugar in the ratio 7 : 2. How much Khoya did she use?
 View Answer
View Answer 
Given,
Quantity of Burfi = 18 kg and Khoya : Sugar = 7 : 2
Total of ratio = 7 + 2 = 9
Quantity of Khoya = (18/9) x 7 = 14kg
So, Reshma used 14 kg Khoya.
Q51: A line segment 56 cm long is to be divided into two parts in the ratio of 2 : 5. Find the length of each part.
 View Answer
View Answer 
Given,
Length of the line segment = 56 cm Ratio of two parts = 2 : 5 Sum of ratios = 2 + 5 = 7
Length of first part = (2/7) x 56 = 16 cm
Length of second part = (5/7) x 56 = 40 cm
Q52: The number of milk teeth in human beings is 20 and the number of permanent teeth is 32. Find the ratio of the number of milk teeth to the number of permanent teeth.
 View Answer
View Answer 
Number of milk teeth in human beings = 20
Number of permanent teeth in human beings = 32
Ratio of the number of milk teeth to the number of permanent teeth = 20/32
= 5/8 [on dividing numerator and denominator by 4]
= 5 : 8
Q53: Sex ratio is defined as the number of females per 1000 males in the population. Find the sex ratio if there are 3732 females per 4000 males in a town.
 View Answer
View Answer 
Sex ratio if there are 3732 females per 4000 males in a town is given as,
= 3732/4000
Q54: In a year, Ravi earns Rs. 360000 and paid Rs. 24000 as income tax. Find the ratio of his
(a) income to income tax.
(b) income tax to income after paying income tax.
 View Answer
View Answer 
(a) Ratio of income to income tax is = 360000/24000
=15/1
(b) Ratio of income tax to income after paying income tax
= 24000/336000
= 3/42
Q55: Ramesh earns Rs 28000 per month. His wife Rama earns Rs 36000 per month. Find the ratio of
(a) Ramesh’s earnings to their total earnings
(b) Rama’s earnings to their total earnings.
 View Answer
View Answer 
(a) Ratio of Ramesh’s earnings to the total earnings of Ramesh and Rama
=28000/64000
=9/16
(b) Ratio of Rama’s earnings to the total earnings of Ramesh and Rama
=36000/64000
= 7/16
Q56: Of the 288 persons working in a company, 112 are men and the remaining are women. Find the ratio of the number of
(a) men to that of women.
(b) men to the total number of persons.
(c) women to the total number of persons.
 View Answer
View Answer 
No. of people working in a company = 288
Total no. of men in the company = 112
Total no. of women in the company = 176
(a) Ratio of the number of men to that of women = 112/176
=7/11
(b) Ratio of the number of women to the total number of persons
= 176/228
=44/57
Q57: A rectangular sheet of paper is of length 1.2 m and width 21 cm. Find the ratio of width of the paper to its length.
 View Answer
View Answer 
Given,
Length of rectangular sheet = 1.2 m [v 1 m = 100 cm]
= 1.2 x 100cm= 120cm Width of rectangular sheet = 21 cm
Ratio of width to length = 21 cm/120 cm
= 7/40 = 7:40 [on dividing numerator and denominator by 3]
Q58: A scooter travels 120km in 3 hours and a train travels 120km in 2 hours. Find the ratio of their speeds.
(Hint: Speed = distance travelled/time taken)
 View Answer
View Answer 
Speed of scooter =120/3 = 40km/h
Speed of train = 120/2 = 60 km/h
Now, ratio of speed of scooter to speed of train = 40/60 = 2/3
Q59: An office opens at 9 a.m. and closes at 5.30 p.m. with a lunch break of 30 minutes. What is the ratio of lunch break to the total period in the office?
 View Answer
View Answer 
As per given information, total period in office = 9 a.m. to 12 p.m. and 12 p.m. to 5 p.m.
This implies total period = 3 hours + 5 hours = 8 hours
Since 1 hour = 60 minutes So, 8 hours = 8 × 60 = 480 minutes
Now, Ratio of lunch interval to total period = 30/480= 1/16
Q60: The shadow of a 3m long stick is 4m long. At the same time of the day, if the shadow of a flagstaff is 24m long, how tall is the flagstaff?
 View Answer
View Answer 
Here given, length of shadow of stick = 4m
Length of stick = 3m
Also, length of shadow of flagstaff = 24m
Now, length of flagstaff =(3 x 24)/4 = 18m
Q61: A recipe calls for 1 cup of milk for every 1 2 2 cups of flour to make a cake that would feed 6persons. How many cups of both flour and milk will be needed to make a similar cake for 8 people?
 View Answer
View Answer 
As given, 1 cup of milk and 2 1/2 cup of flour to make cake for six persons.
For one person, the ingredients required will be, Milk = 1/6cup
Flour = 5/12 cups
Now, for 8 people, milk 8 x (1/6) = 4/3 cups
Flour = 10/3 cups
Therefore, we need 4/3 cups of milk and 10/3 cups of flour to make cake for eight people.
Q62: In a school, the ratio of the number of large classrooms to small classrooms is 3 : 4. If the number of small rooms is 20, then find the number of large rooms.
 View Answer
View Answer 
Given, ratio of number of large classrooms to small classrooms = 3:4 Number of small classrooms = 20 Let the classrooms are multiple of x.
So, large classrooms = 3x Small classrooms = 4x
According to the question, 4x = 20 => x=20/4 = 5 .
Hence, number of large classrooms = 3x
= 3 x 5 = 15
Q63: Samira sells newspapers at Janpath crossing daily. On a particular day, she had 312 newspapers out of which 216 are in English and remaining in Hindi.
Find the ratio of
(a) the number of English newspapers to the number of Hindi newspapers.
(b) the number of Hindi newspapers to the total number of newspapers.
 View Answer
View Answer 
Given, total newspapers = 312 English newspapers = 216
Hindi newspapers = Total number of newspapers – Newspapers in English = 312 – 216 = 96
(a) Ratio of number of English newspapers to number of Hindi newspapers = 216/96
= 9/4 = 9:4 [on dividing numerator and denominator by 24]
(b) Ratio of number of Hindi newspapers to the total number of newspapers = 96/312
= 4/13 = 4:13.
Q64: The students of a school belong to different religious backgrounds. The number of Hindu students is 288, the number of Muslim students is 252, the number of Sikh students is 144 and the number of Christian students is 72.
Find the ratio of
(a) the number of Hindu students to the number of Christian students.
(b) the number of Muslim students to the total number of students.
 View Answer
View Answer 
Given, number of Hindu students = 288 Number of Muslim students = 252 Number of Sikh students = 144 Number of Christian students = 72 Total number of students = 288+252+144+72 =756
(a) Ratio of number of Hindu students to the number of Christian students = 288/72
= 4/1 = 4:1 [on dividing numerator and denominator by 72]
(b) Ratio of number of Muslim students to the total number of students = 252/756
= 1/3 =1:3 [on dividing numerator and denominator by 252]
Q65: When Chinmay visited Chowpati at Mumbai on a holiday, he observed that the ratio of North Indian food stalls to South Indian food stalls is 5:4. If the total number of food stalls is 117, find the number of each type of food stalls.
 View Answer
View Answer 
Given, ratio of North Indian food stalls to South Indian food stalls = 5:4
Total number of food stalls =117
Total ratio = 5+4 = 9
North Indian food stalls = (5/9) x 117 = 65
South Indian food stalls = (4/9) x 117 = 52
Q66: At the parking stand of Ramleela ground, Kartik counted that there are 115 cycles, 75 scooters and 45 bikes. Find the ratio of the number of cycles to the total number of vehicles.
 View Answer
View Answer 
Given, at parking stand, number of Cycles = 115
Scooters = 75
Bikes = 45
Total number of vehicles = 115+75+ 45 = 235
Ratio of number of cycles to the total number of vehicles = 115/235
= 23/47 =23:47
[on dividing numerator and denominator by 5]
Q67: A train takes 2 hours to travel from Ajmer to Jaipur, which are 130km apart. How much time will it take to travel from Delhi to Bhopal which are 780km apart if the train is travelling at the uniform speed?
 View Answer
View Answer 
Time taken to travel from Ajmer to Jaipur = 2 hours
Distance between Ajmer and Jaipur = 130 km
Also, Distance between Delhi and Bhopal = 780km
Now, speed of train = 130/2 km/h = 65km/h
Thus, time taken by train to travel from Delhi to Bhopal = 780/65 =12 hours
Q68: The length and breadth of a school ground are 150m and 90m respectively, while the length and breadth of a mela ground are 210m and 126m, respectively. Are these measurements in proportion?
 View Answer
View Answer 
Ratio of length and breadth of a school ground = 150/90 = 5/3
Also, ratio of length and breadth of a mela ground = 210/126 = 5/3
Thus, the given measurements are in proportion.
Q69: In Fig. 8.4, the comparative areas of the continents are given: What is the ratio of the areas of
(a) Africa to Europe
(b) Australia to Asia
(c) Antarctica to Combined area of North America and South America.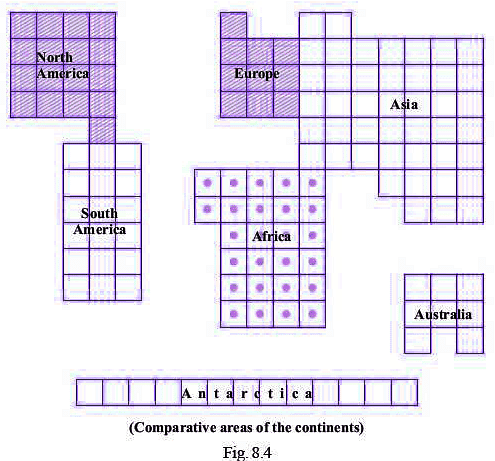
 View Answer
View Answer 
(a) From given figures, ratio of areas of Africa to Europe =13/5
(b) From given figures, ratio of areas of Australia to Asia = 2/11
(c) From given figures, ratio of areas of Antarctica to Combined area of North America and South America = 13/35
Q70: A tea merchant blends two varieties of tea costing it Rs. 234 and Rs. 130 per kg in the ratio of their costs. If the weight of the mixture is 84 kg, then find the weight of each variety of tea.
 View Answer
View Answer 
Given, cost of two varities of tea = Rs. 234 and Rs. 130
Ratio of their costs = 234/130 = 9/5 = 9:5
[on dividing numerator and denominator by 26]
Total weight of mixture = 84 kg Total ratio = 9+5 = 14
Weight of first variety tea = (9/14) x 84 = 54 kg
Weight of second variety tea = (5/14) x 84 = 30 kg
Q71: An alloy contains only Zinc and Copper and they are in the ratio of 7:9. If the weight of the alloy is 8 kg, then find the weight of Copper in the alloy.
 View Answer
View Answer 
Given, the ratio of Zinc and Copper in alloy = 7:9 and weight of alloy = 8 kg
Let the weight of Zinc and Copper in alloy be 7x and 9x respectively, where x is multiple of weight.
Then, total weight =7x+9x = 6x
16x = 8 kg => x = ½ kg
Weight of copper = 9x = 9 x (1/2) = 4 ½ kg Hence, the weight of copper is 4 ½ kg.
Q72: In the following figure, each division represents 1cm:

Express numerically the ratios of the following distances:
(i) AC : AF
(ii) AG : AD
(iii) BF : AI
(iv) CE : DI
 View Answer
View Answer 
(i) AC/AF = 2/5
(ii) AG/AD = 2/1
(iii) BF/AI = 1/2
(iv) CE/DI = 2/5
Q73: Find two numbers, whose sum is 100 and whose ratio is 9:16.
 View Answer
View Answer 
Let the two numbers are 9x and 16x, whose sum is 100.
⇒ 9x +16x = 100
⇒ 25x = 100
⇒ x = 4
Q74: In Fig. 8.6 (i) and Fig. 8.6 (ii), find the ratio of the area of the shaded portion to that of the whole figure: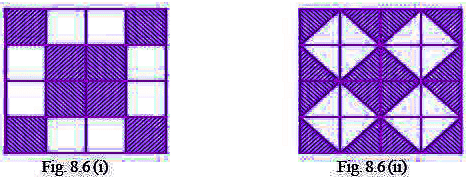
 View Answer
View Answer 
(i) Ratio of the area of the shaded portion to that of the whole figure
= 8/16
= 1/2
(ii) Ratio of the area of the shaded portion to that of the whole figure
= 16/32
= 1/2
Q75: A typist has to type a manuscript of 40 pages. She has typed 30 pages of the manuscript. What is the ratio of the number of pages typed to the number of pages left?
 View Answer
View Answer 
Total pages of manuscript to type = 40
Typed pages of manuscript = 30
Left pages = 40 – 30 = 10
Ratio of the number of pages to the types pages to the number of left pages = 30/10 = 3/1 = 3:1 .
Q76: In a floral design made from tiles each of dimensions 40cm by 60cm (See Fig. 8.7), find the ratios of:
(a) the perimeter of shaded portion to the perimeter of the whole design.
(b) the area of the shaded portion to the area of the unshaded portion.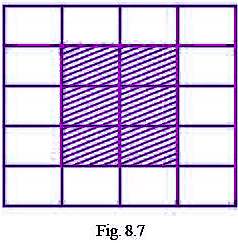
 View Answer
View Answer 
(a) Perimeter of shaded region = 2(20 + 36) = 112cm
Also, perimeter of whole design = 2 (40 + 60) = 200cm
ow, ratio of the perimeter of shaded portion to the perimeter of the whole design = 112/200 = 14/25
(b) Area of shaded portion = 20 x 36 = 720 sq.cm.
Area of unshaded portion = (40 x 60) - 720 = 1680 sq.cm.
Now, ratio of the area of the shaded portion to the area of the unshaded portion = 720/1680 = 3/7
Q77: In Fig. 8.8, what is the ratio of the areas of
(a) shaded portion I to shaded portion II ?
(b) shaded portion II to shaded portion III?
(c) shaded portions I and II taken together and shaded portion III?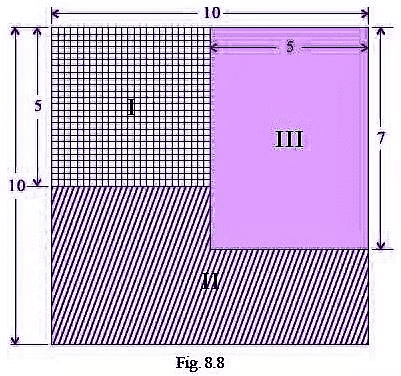
 View Answer
View Answer 
(a) Ratio of the areas of shaded portion I to shaded portion II is = 5/8
(b) Ratio of the areas of shaded portion II to shaded portion III = 8/7
(c) Ratio of the areas of shaded portions I and II taken together and shaded portion III = 13/7
Q78: A car can travel 240km in 15 litres of petrol. How much distance will it travel in 25 litres of petrol?
 View Answer
View Answer 
Distance travelled by car in 15 litres of petrol = 240km
Distance travelled by car in 25 litres of petrol = (240/15) x 25 = 400km
Q79: Bachhu Manjhi earns Rs. 24000 in 8 months. At this rate,
(a) how much does he earn in one year?
(b) in how many months does he earn Rs. 42000?
 View Answer
View Answer 
Money earned by Bachhu Manjhi in 8 months = Rs. 24000
(a) Money earned by Bachhu Manjhi in 12 months = (24000/8) x 12 = Rs. 36000
(b) Rs 24000 earned by Bachhu Manjhi in = 8 months
Rs 42000 earned by Bachhu Manjhi in = (8/24000) x 42000 = 16 months
Q80: The yield of wheat from 8 hectares of land is 360 quintals. Find the number of hectares of land required for a yield of 540 quintals?
 View Answer
View Answer 
360 quintals yield of wheat is obtained from = 8 hectares
540 quintals yield of wheat is obtained from = (8/360) x 540 = 12 hectares
Q81: The earth rotates 360º about its axis in about 24 hours. By how much degree will it rotate in 2 hours?
 View Answer
View Answer 
In 24 hours, Earth rotates by = 360 degrees
In 2 hours. Earth rotates by = (360/24) x 2 = 30 degrees
Q82: Shivangi is suffering from anaemia as haemoglobin level in her blood is lower than the normal range. Doctor advised her to take one iron tablet two times a day. If the cost of 10 tablets is Rs. 17, then what amount will she be required to pay for her medical bill for 15 days?
 View Answer
View Answer 
Tablets required per day = 2
Tablets required for 15 days = 15 x 2 = 30
Now cost of 10 tablets = Rs. 17
Cost of 30 tablets = (17/10) x30 = 51
Q83: The quarterly school fee in Kendriya Vidyalaya for Class VI is Rs 540. What will be the fee for seven months?
 View Answer
View Answer 
Quarterly fee for class VI = Rs 540
Fee for seven months = (540/4) x 7= Rs. 945
Q84: In an election, the votes cast for two of the candidates were in the ratio 5 : 7. If the successful candidate received 20734 votes, how many votes did his opponent receive?
 View Answer
View Answer 
As given, votes cast for two of the candidates were in the ratio = 5:7
Let votes received by the two candidates = 5x and 7x
Also, votes received by successful candidates = 20734
This implies, 7x = 20734 x = 2962
Votes received by the opponent = 5 x 2962 = 14810
Q85: A metal pipe 3 metre long was found to weigh 7.6kg. What would be the weight of the same kind of 7.8m long pipe?
 View Answer
View Answer 
Weight of 3 metre long pipe = 7.6kg
Weight of 7.8 m long pipe = (7.6/3) x 7.8 = 19.76 kg
Q86: A recipe for raspberry jelly calls for 5 cups of raspberry juice and 2(1/2) cups of sugar. Find the amount of sugar needed for 6 cups of the juice?
 View Answer
View Answer 
5 cups of raspberry juice requires sugar = 5/2 cups
6 cups of raspberry juice requires sugar = 5/(2x5) x 6 = 3 cups
Q87: A farmer planted 1890 tomato plants in a field in rows each having 63 plants. A certain type of worm destroyed 18 plants in each row. How many plants did the worm destroy in the whole field?
 View Answer
View Answer 
Consider the number of rows = x
This implies, total no. of plants = (number of plant in each row) x (number of rows)
1890 = 63x
x = 1890/63 = 30
So, no. of rows = 30
Plants destroyed by worm in each row = 18
Thus total plants destroyed by worm = 18x30 = 540
Q88: Length and breadth of the floor of a room are 5m and 3m, respectively. forty tiles, each with area 1/16 m2 are used to cover the floor partially. Find the ratio of the tiled and the non-tiled portion of the floor.
 View Answer
View Answer 
Given, length and breadth of the floor of a room = 5m and 3m So area of the floor = 3 x 5 = 15sqm
Also area of one tile = 1/16 sqm
So, area of floor covered by 40 tiles = (1/16) x 40 = 5/2 sqm
Area of floor not covered by tiles = 15 - 5/2 = 25/2 sqm
Now, ratio of the tiled and the non-tiled portion of the floor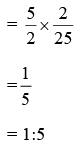
Q89: A carpenter had a board which measured 3m × 2m. She cut out a rectangular piece of 250cm × 90cm. What is the ratio of the area of cut out piece and the remaining piece?
 View Answer
View Answer 
Measurement of the board = 3m x 2m
So, area of the board = 300cm x 200cm = 60000 sqm
Measurement of rectangular piece cut down from board = 250cm × 90cm
So, area of rectangular piece cut down from board = 22500 sqcm
Area of remaining portion of the board = 60000 - 22500 = 37500 sqcm
Now, ratio of the area of cut out piece and the remaining piece = 22500/37500.
|
48 videos|331 docs|23 tests
|
FAQs on NCERT Exemplar Solutions: Ratio & Proportion - Mathematics for Class 6
| 1. What is the definition of ratio in mathematics? |  |
| 2. How do you simplify a ratio? |  |
| 3. What is the difference between ratio and proportion? |  |
| 4. How can ratios be used in real-life situations? |  |
| 5. What is an example of a proportion problem? |  |






















