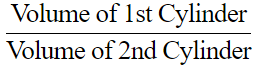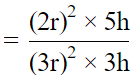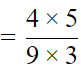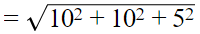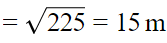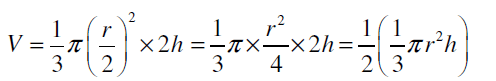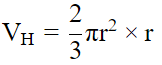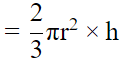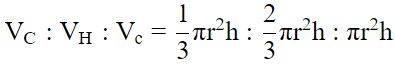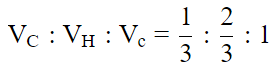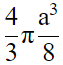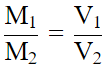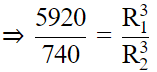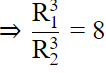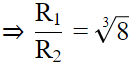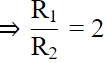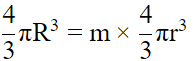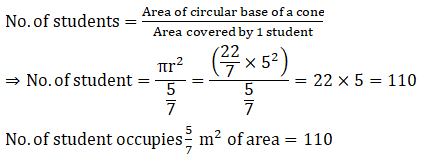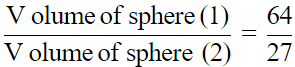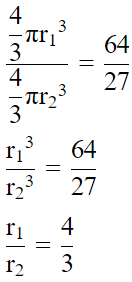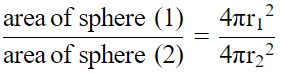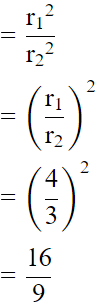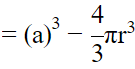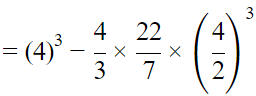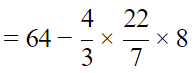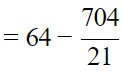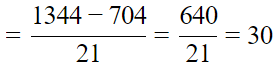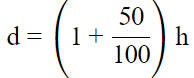NCERT Exemplar Solutions: Surface Area & Volume | Mathematics (Maths) Class 9 PDF Download
Exercise 13.1 Page No. 122
Write the correct answer in each of the following:
Q.1. The radius of a sphere is 2r, then its volume will be
(a) 4 / 3 πr3
(b) 4πr3
(c) 8πr3 / 3
(d) 32 / 3 πr3
The correct answer is Option (d)
Given, the radius of a sphere is 2r.
The volume of a sphere = (4 / 3) × (radius)3
Thus, the volume of the given sphere
= (4 / 3) × π × (2r)3 = (4 / 3) × π × 8 × r3
= (32 π r3 / 3)
Hence, option (d) is the correct answer.
Q.2. The total surface area of a cube is 96 cm2. The volume of the cube is:
(a) 8 cm3
(b) 512 cm3
(c) 64 cm3
(d) 27 cm3
The correct answer is Option (c)
The surface area of a cube is 96 cm2
Let the length of the cube be l cm.
Thus,
6 × l2 = 96
According to formula
l2 = 96 / 6
l2 = 16
l = 4
Thus the length of the cube is 4 cm.
Volume of a cube = l3
= 43
= 64
Thus the volume is 64 cm3.
Q.3. A cone is 8.4 cm high and the radius of its base is 2.1 cm. It is melted and recast into a sphere. The radius of the sphere is:
(a) 4.2 cm
(b) 2.1 cm
(c) 2.4 cm
(d) 1.6 cm
The correct answer is Option (b).
Height of cone, h = 8.4cm
The radius of base, r = 2.1cm
Thus volume of a cone = (1 / 3) × π × h × r2
= (1 / 3) × π × 8.4 × (2.1)2
Now when it is melted to form a sphere, say of radius r1 cm, the volumes of both are going to be equal.
Volume of sphere = (4 / 3) × π × r13
∴ 4 / 3 π x r13 = 1 / 3 π x 2.12 x 8.4
= 2.12 x 8.4
r31 = 2.12 x 2.1
r31 = 2.13
∴ r1 = 2.1cm
Thus the radius of the sphere is 2.1 cm.
Q.4. In a cylinder, radius is doubled and height is halved, curved surface area will be
(a) halved
(b) doubled
(c) same
(d) four times
The correct answer is Option (c).
Let the radius of a cylinder = r unit
Let the height of a cylinder = h unit.
According to question,
Radius is doubled = 2r
Height is halved = h / 2
Then,
Curved surface area of a cylinder = 2 × π × r × h
And according to the above condition,
Curved surface area = 2 × π × 2 × r × h / 2
= 2 × π × r × h
This is the same as the curved surface area of the cylinder with radius r and height h.
Q.5. The total surface area of a cone whose radius is r / 2 and slant height 2l is
(a) 2πr (l + r)
(b) πr(l + r / 4)
(c) πr(l + r)
(d) 2πrl
The correct answer is Option (b).
Given, radius of a cone is r / 2 and slant height is 2L.
Total surface area = π × radius × slant height + π × radius2
Hence, option (b) is the correct answer.
Q.6. The radii of two cylinders are in the ratio of 2:3 and their heights are in the ratio of 5:3. The ratio of their volumes is:
(a) 10 : 17
(b) 20 : 27
(c) 17 : 27
(d) 20 : 37
The correct answer is Option (b).
Step 1: Calculate Ratio of Volume by the help of Ratio of Radius and Height
Given: Ratio of Radii of two Cylinder is 2:3
Let the Common Multiple of Radius be r
⇒ Radius of 1st cylinder be 2r
⇒ Radius of 2nd Cylinder = 3r
Given: The ratio of Heights of Two Cylinder is 5:3.
Let the Common Multiple of Height be h
⇒ Height of 1st Cylinder = 5h
⇒ Height of 2nd Cylinder = 3h
∴ Ratio of volume =[Since the volume of a cylinder=πr2h]
= 20/27
Therefore, the Ratio of Volume of Two Cylinders is 20:27.
Q.7. The lateral surface area of a cube is 256 m2. The volume of the cube is
(a) 512 m3
(b) 64 m3
(c) 216 m3
(d) 256 m3
The correct answer is Option (a)
Given, the lateral surface area of a cube = 256 m2.
We know that the lateral surface area of cube =4(edge)2.
∴ 4(edge)2 = 256
⇒ (edge)2 = 256/4
⇒ (edge)2 = 64
⇒ edge = 8.
Also, volume of cube = (edge)3.
∴ Volume of cube = (8)3 = 512 m3.
Therefore, option (a) is correct.
Q.8. The number of planks of dimensions (4 m × 50 cm × 20 cm) that can be stored in a pit which is 16 m long, 12m wide and 4 m deep is
(a) 1900
(b) 1920
(c) 1800
(d) 1840
The correct answer is Option (b)
Given: the number of planks of dimensions (4m ×50 cm ×20 cm )
Volume of planks = lbh = 400(50)20 = 400000 cm3
Volume of pits = 1600(1200)400 = 768000000 cm3
Number of planks = 786000000/400000 = 1920.
Q.9. The length of the longest pole that can be put in a room of dimensions (10 m × 10 m × 5m) is
(a) 15 m
(b) 16 m
(c) 10 m
(d) 12 m
The correct answer is Option (b).
Longest pole can be faced along the diagonal and its length
Q.10. The radius of a hemispherical balloon increases from 6 cm to 12 cm as air is being pumped into it. The ratios of the surface areas of the balloon in the two cases is
(a) 1 : 4
(b) 1 : 3
(c) 2 : 3
(d) 2 : 1
The correct answer is Option (a).
Total surface area of a Hemisphere = 2πr2 + πr2 = 3πr2
r = 6, Surface area = 3π(6)2 =36
r = 12, Surface area=3π(12)2 = 144
Ratio = 36:144
= 1 : 4
Exercise 13.2 Page No: 124
Write True or False and justify your answer in each of the following:
Q.1. The volume of a sphere is equal to two-third of the volume of a cylinder whose height and diameter are equal to the diameter of the sphere.
True
Let the radius of the sphere = r.
According to the question,
height and diameter of cylinder = diameter of sphere.
So, the radius of the cylinder = r
And, the height of the cylinder = 2r
We know that,
Volume of sphere = 2 / 3 volume of cylinder
⇒ 4 / 3 πr3 = 2 / 3(πr2 x 2r) = 4 / 3 πr3
Hence, the given statement “the volume of a sphere is equal to two-third of the volume of a cylinder whose height and diameter are equal to the diameter of the sphere” is true.
Q.2. If the radius of a right circular cone is halved and height is doubled, the volume will remain unchanged.
False
Let the original radius of the cone = r
Let height of the cone = h.
The volume of cone = 1 / 3 πr2h
Now, when radius of a height circular cone is halved and height is doubled, then
We can observe that the new volume = half of the original volume.
Hence, the given statement “if the radius of a right circular cone is halved and height is doubled, the volume will remain unchanged” is false.
Q.3. In a right circular cone, height, radius and slant height do not always be sides of a right triangle.
True
Consider a right circular cone, with
Height = h
Radius = r
And slant height = l
We know, right triangle = one angle 90°
Using Pythagoras theorem in
⇒ l2 = h2 + r2
This justifies that height, radius and slant height of cone can always be the sides of a right triangle.
Hence, the given statement “in a right circular cone, height, radius and slant height do not always be sides of a right triangle” is true.
Q.4. If the radius of a cylinder is doubled and its curved surface area is not changed, the height must be halved.
True
Let radius of the cylinder = r
Height of the cylinder = h
Then, curved surface area of the cylinder, CSA = 2πrh
According to the question, Radius is doubled and curved surface area is not changed.
New radius of the cylinder, R = 2r
New curved surface area of the cylinder, CSA’ = 2πrh …(i)
Alternate case:
When R = 2r and CSA’ = 2πrh
But curved surface area of cylinder in this case, CSA’= 2πRh = 2π(2r)h = 4πrh …(ii)
Comparing equations (i) and (ii),
We get,
Since, 2πrh ≠ 4πrh
equation (i) ≠ equation (ii)
Thus, if h = h / 2 (height is halved)
Then,
CSA’ = 2π(2r)(h / 2) = 2πrh
Hence, the given statement “If the radius of a cylinder is doubled and its curved surface area is not changed, the height must be halved” is true.
Q.5. The volume of the largest right circular cone that can be fitted in a cube whose edge is 2r equals to the volume of a hemisphere of radius r.
True
According to the question,
Edge of cube, l = 2r
Then, diameter of the cone = 2r
⇒ radius of the cone = 2r / 2
= r
Height of the cone, h = height of the cube
= 2r
Volume of the cone is given by,
Volume of cone = 1 / 3 πr2h
= 1 / 3 πr2(2r)
= 2 / 3 πr3
= Volume of hemisphere of radius r
Hence, the given statement “the volume of the largest right circular cone that can be fitted in a cube whose edge is 2r equals to the volume of a hemisphere of radius r” is true.
Q.6. A cylinder and a right circular cone are having the same base and same height. The volume of the cylinder is three times the volume of the cone.
True
Let the radius of the base of a cylinder and a right circular cone be r and height be h.
Then, volume of the cylinder = πr2h
Volume of the cone = (1/3)πr2h
∴ Volume of the cylinder = 3 × Volume of the cone
Q.7. A cone, a hemisphere and a cylinder stand on equal bases and have the same height. The ratio of their volumes is 1 : 2 : 3.
TrueGiven: A cone, a hemisphere, and a cylinder stand on equal bases.
Hence radius of base of cone = radius of hemisphere = radius of cylinder = r
And,
They also have same height = h
Hight of cone = h
Hight of cylinder= h
Hight of Hemisphere r = h (r is the radius of sphere)
Now,
Volume of cone VC = (1/3) πr2h ...(1)
Volume of hemisphere...(2)
Volume of cylinder Vc = πr2h ...(3)
From equation 1, 2 and 3
VC : VH : Vc = 1 : 2 : 3
Q.8. If the length of the diagonal of a cube is 6√3 cm, then the length of the edge of the cube is 3 cm.
FalseThe diagonal of cube with side a is given as a√3
The diagonal of the given cube is 6√3
⇒ a√3 = 6√3
So the side of the cube is 6 cm.
Q.9. If a sphere is inscribed in a cube, then the ratio of the volume of the cube to the volume of the sphere will be 6 : π.
TrueLet the length of side of cube be a.
∴ V1 (Volume of cube) = a3
Now, Length of side of cube = Diameter of the sphere = a
Hence, Radius of sphere = (a/2).
V2 (Volume of sphere) =
Ratio of
Q.10. If the radius of a cylinder is doubled and height is halved, the volume will be doubled.
TrueLet the radius of the cylinder be r and height be h.
Then, volume of the cylinder, V1 = πr2h
New radius, R = 2r
New height of the cylinder, H = (h/2)
∴ Volume of a cylinder,
V2 = πr2h = π(2r)2(h/2)
= π × 4r2 × (h/2)
= 2πr2h
= 2V1
Hence, if the radius of a cylinder is doubled and height of a cylinder is halved, the volume of the cylinder is doubled.
Exercise 13.3 Page No: 126
Q.1. Metal spheres, each of radius 2 cm, are packed into a rectangular box of internal dimensions 16 cm × 8 cm × 8 cm. When 16 spheres are packed the box is filled with preservative liquid. Find the volume of this liquid. Give your answer to the nearest integer. [Use π = 3.14]
According to the question,
The radius of each sphere, r = 2 cm
The volume of a sphere is given by
Volume of 1 sphere = 4 / 3 πr3
Since there are 16 spheres in our question,
Volume of 16 spheres = 16 × 4 / 3 πr3
= 16 × 4 / 3 × 3.14 × 23 = 535.89 cm3
We know that,
Dimensions of rectangular box = 16 cm × 8 cm × 8 cm
Volume of rectangular box = 16 × 8 × 8 = 1024 cm3
In order to find the volume of the liquid that is filled in rectangular box,
We need to find the space left in the rectangular box after the space occupied by the spheres.
So, we can say that,
Volume of the liquid = (Volume of the rectangular box) – (Volume of the 16 spheres)
⇒ Volume of the liquid = 1024 – 535.89
= 488.11 cm3
Thus, the volume of this liquid is 488.11 cm3.
Q.2. A storage tank is in the form of a cube. When it is full of water, the volume of water is 15.625 m3. If the present depth of water is 1.3 m, find the volume of water already used from the tank.
When the cubical tank is full:
Volume of water = Volume of cube = 15.625 m3
So, we know that,
Volume of cube = (length of edge of cube)3
⇒ (length of edge of cube)3 = 15.625
⇒ length of edge of cube = ∛15.625
= 2.5 m
We know that,
Length of the edge of the cube = 2.5 m.
When the present depth of the water is 1.3 m:
Length of tank = 2.5 m
Breadth of tank = 2.5 m
So, volume of water upto 1.3 m depth = length × breadth × depth
= 2.5 × 2.5 × 1.3 = 8.125 m3
Then, volume of water already used from the tank = (Volume of tank when it was full of water) – (Volume of water when depth is 1.3 m)
= 15.625 – 8.125 = 7.5 m3
Thus, volume of water already used from the tank is 7.5 m3.
Q.3. Find the amount of water displaced by a solid spherical ball of diameter 4.2 cm, when it is completely immersed in water.
Water displaced when a solid spherical ball is immersed completely in water equals to its own volume.
According to the question,
Diameter of spherical ball = 4.2 cm
⇒ radius of spherical ball = 4.2 / 2 = 2.1 cm
So, volume of a sphere = 4 / 3 πr3
(4 / 3) (22 / 7)(2.1)3 = 38.81
Thus, volume of water displaced is 38.81 cm3.
Q.4. How many square metres of canvas is required for a conical tent whose height is 3.5 m and the radius of the base is 12 m?
According to the question,
Dimensions of conical tent are:
Height = 3.5 m
Radius = 12 m
Curved surface area of cone = πr√(r2 + h2)
= 22 / 7 × 12 √(122 + 3.52)
= 22 / 7 × 12 × √156.25
= 22 / 7 × 12 × 12.5
= 471.43 m2
Since, area of canvas = curved surface area of conical tent
Therefore, area of canvas required is 471.43 m2.
Q.5. Two solid spheres made of the same metal have weights 5920 g and 740 g, respectively. Determine the radius of the larger sphere, if the diameter of the smaller one is 5 cm.
Mass is directly proportional to volume for same metal (Density)
Let Mass of Solid 1 be M1, Volume be V1, Mass of Solid 2 be M2 and Volume be V2Now
Volume of sphere is directly proportional to R3
So,
So, R1 = R2 × 2
So, R1 =2.5 × 2 = 5 cm.
Q.6. A school provides milk to the students daily in a cylindrical glasses of diameter 7 cm. If the glass is filled with milk upto an height of 12 cm, find how many litres of milk is needed to serve 1600 students.
Volume of milk in 1 glass = πr2h
= π × (3.5)2 × 12 = 461.58cm2
for 1600 students milk needed is
= 1600 × 461.58
= 738258 litres.
Q.7. A cylindrical roller 2.5 m in length, 1.75 m in radius when rolled on a road was found to cover the area of 5500 m2. How many revolutions did it make?
Area covered by cylindrical roller in one revolution = Curved surface area of cylinder
Curved surface of cylinder = 2πr × l = 2π × (1.75)(2.5) = 27.5 m2
Revolution = (Total Area/ Area covered in one revolution) = 5500/27.5 = 200.
Q.8. A small village, having a population of 5000, requires 75 litres of water per head per day. The village has got an overhead tank of measurement 40 m × 25 m × 15 m. For how many days will the water of this tank last?
Volume of tank =(40)(25)(15)=15000 m3=150000001
Water to population required per day =5000(75)=3750001
Water tank Last for = (15000000/375000) = 40 days.
Q.9. A shopkeeper has one spherical laddoo of radius 5 cm. With the same amount of material, how many laddoos of radius 2.5 cm can be made?
Volume of 1 larger laddoo = Volume of m nos. of smaller laddoos
Therefore,
⇒ 125 = m × (25/10)3
⇒ m = 8
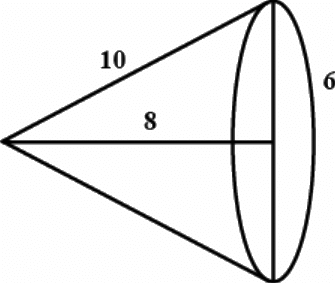
Q.10. A right triangle with sides 6 cm, 8 cm and 10 cm is revolved about the side 8 cm. Find the volume and the curved surface of the solid so formed.
After Drawing the figure we come to know that a cone if formed whose
l = 10 cm , h = 8 cm , r = 6 cm
Curved surface of the solid (CONE ) = πrl
A = πrl = 22/7 ∗ 10 ∗ 6 = 188.57 cm2
Exercise 13.4 Page No: 127
Q.1. A cylindrical tube opened at both the ends is made of iron sheet which is 2 cm thick. If the outer diameter is 16 cm and its length is 100 cm, find how many cubic centimeters of iron has been used in making the tube?
According to the question,
Outer diameter d = 16cm
Then,
Outer radius r – 16 / 2 = 8cm
Height = length = 100cm
Thickness of iron sheet = 2cm
Volume of cylinder = πr2h, where r = outer radius and π = 3.14
Thus, Volume of cylinder = πr2h
= 3.14 × (8)2 × 100
= 20,096 cm3
Now, inner diameter = outer diameter – 2 × thickness of iron sheet Inner diameter = 16 - (2 × 2) = 12cm
Inner radius R = 12 / 2 = 6cm
Thus, Volume of hollow space = πR2h, where R = inner radius and π = 3.14
= πR2h
= 3.14 × (6)2 × 100 = 11,304 cm3
Thus,
Volume of iron used = Volume of cylinder – Volume of hollow space
= (20,096 – 11,304 ) cm3
= 8800 cm3.
Q.2. A semi-circular sheet of metal of diameter 28cm is bent to form an open conical cup. Find the capacity of the cup.
According to the question,
Diameter of semi circular sheet = 28cm
Radius of semi circular sheet (r) = 28 / 2
= 14cm
Semi Circular sheet is bent to form an open conical cup
Thus, slant height of a conical cup (l) = radius of semicircular sheet(r) = 14cm
We know that,
Circumference of base of a cone = 2πR,
(where, R = radius of a cone and circumference of semi circle = πr)
Thus,
Circumference of base of a cone = Circumference of a Semi circle
⇒ 2πR = πr
⇒ R = πr / 2π = r / 2 = 14 / 2 = 7 cm
To find height, we use the Pythagorean theorem: R2 + h2 = l2
Where,
R = radius of a cone
h = height of a cone
l = slant height of a cone
⇒ (7)2 + h2 = (14)2
⇒ 49 + h2 = 196
⇒ h2 = 196 – 49 = 147
⇒ h = √147 = 7√3 cm
Thus, volume of a cone = 1 / 3 πR2h
⇒ Volume of a cone = (1 / 3) x (22 / 7) x 49 x 7√3 = 1078√3 / 3 cm3
⇒ 622.38 cm3
Q.3. A cloth having an area of 165 m2 is shaped into the form of a conical tent of radius 5 m
(i) How many students can sit in the tent if a student, on an average, occupies 5 / 7 m2 on the ground?
(ii) Find the volume of the cone.
According to the question,
Area of cloth = 165m2
Radius of conical tent = 5m
Area covered by 1 student = 5 / 7 m2
Curved surface area of cone = πrl
Thus, curved surface area of a conical; tent = πrl
⇒ 165 = 22 / 7 x 5 x 1
⇒ l = 165 x 7 / 22 x 5 = 21 / 2 = 10.5 m
(i)
(ii) Height of a cone
r2 + h2 = l2
Where,
r = radius of a cone
h = height of a cone
l = slant height of a cone
⇒ (5)2 + h2 = (10.5)2
⇒ 25 + h2 = 110.25
⇒ h2 = 110.25 – 25 = 85.25
⇒ h = √85.25 = 9.23 m
Volume of a cone = (1 / 3) πr2h
= 1 / 3 x 22 / 7 x 52 x 9.23 = 5076.5 / 21 = 241.73 m3
Q.4. The water for a factory is stored in a hemispherical tank whose internal diameter is 14 m. The tank contains 50 kilolitres of water. Water is pumped into the tank to fill to its capacity. Calculate the volume of water pumped into the tank.
According to the question,
Internal diameter of hemispherical tank = 14 m
Internal radius of hemispherical tank = 14 / 2 m = 7m
Tank contains 50kl = 50m3 of water (since, 1kl = 1m3)
Volume of a hemispherical tank = 2 / 3 πr3
Volume of a hemispherical tank = 2 / 3 x 22 / 7 x (7)3 = 2156 / 3 = 718.66 m3
Volume of water pumped into the tank = Volume of hemispherical tank – 50m3
= 718.66 – 50
= 668.66 m3
Q.5. The volumes of the two spheres are in the ratio 64 : 27. Find the ratio of their surface areas.
Given that,
Volume of two sphere are in ratio = 64 : 27
We know that,
Volume of sphere = (4/3)πr3
Then,
Then, Ratio of areas both spheres
Hence, this is the answer.
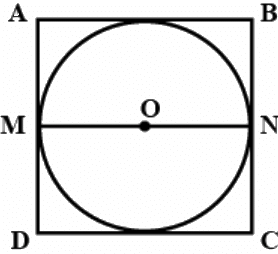
Q.6. A cube of side 4 cm contains a sphere touching its sides. Find the volume of the gap in between.
Let ABCD be cube which contain sphere touching its sides. The diameter of sphere is the sides of the cube.
Now,
The volume of the gap in between cube and sphere = volume of cube -volume of sphere
= 30 cm3
Q.7. A sphere and a right circular cylinder of the same radius have equal volumes. By what percentage does the diameter of the cylinder exceed its height?
The volume of sphere = The volume of cylinder
(4/3)πr3 = πr2h
(4/3)r = h
4r = 3h
2(2r) = 3h ...(∵ d = 2r)
⇒ 2d = 3h
d = 1.5h = (1 + 0.5)h
The diameter exceeds the height by 50%.
Q.8. 30 circular plates, each of radius 14 cm and thickness 3cm are placed one above the another to form a cylindrical solid. Find :
(i) the total surface area
(ii) volume of the cylinder so formed.
Given, radius 14 cm, thickness = 3 cm, number of plates = 30
Therefore, height of cylinder will be 3 × 30 = 90 cm
We know, total surface area of cylinder = 2πr(r + h) cm2
Therefore, total surface area = 2π(14)(14 + (90)) = 9152 cm2
|
40 videos|563 docs|57 tests
|
FAQs on NCERT Exemplar Solutions: Surface Area & Volume - Mathematics (Maths) Class 9
| 1. What is the formula for calculating the surface area of a cylinder? |  |
| 2. How do you find the volume of a cone? |  |
| 3. What is the relationship between surface area and volume for three-dimensional shapes? |  |
| 4. How can you derive the surface area of a sphere? |  |
| 5. What is the importance of understanding surface area and volume in real-life applications? |  |