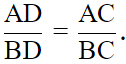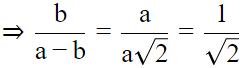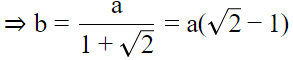NCERT Exemplar Solutions: Triangles | Mathematics (Maths) Class 9 PDF Download
| Table of contents |

|
| Exercise 7.1 Page No: 64 |

|
| Exercise 7.2 Page No: 65 |

|
| Exercise 7.3 Page No: 67 |

|
| Exercise 7.4 Page No: 69 |

|
Exercise 7.1 Page No: 64
In each of the following, write the correct answer:
Q.1. Which of the following is not a criterion for congruence of triangles?
(a) SAS
(b) ASA
(c) SSA
(d) SSS
Correct Answer is Option (c)
We know that,
Two triangles are congruent, if the side(S) and angles (A) of one triangle is equal to another.
And criterion for congruence of triangle are SAS, ASA, SSS, and RHS.
SSA is not the criterion for congruency of a triangle.
Hence, option (c) is the correct answer.
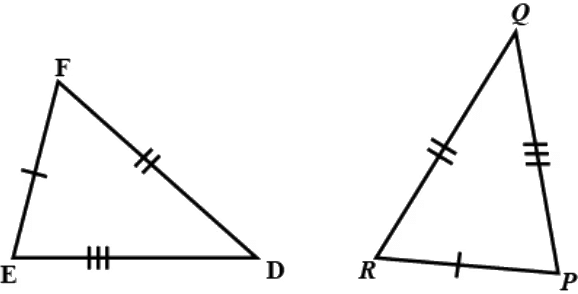
Q.2. If AB = QR, BC = PR and CA = PQ, then
(a) ΔABC ≅ ΔPQR
(b) ΔCBA ≅ ΔPRQ
(c) ΔBAC ≅ ΔRPQ
(d) ΔPQR ≅ ΔBCA
Correct Answer is Option (b)
According to the question,
AB = QR, BC = PR and CA = PQ
Since, AB = QR, BC = PR and CA = PQ
We can say that,
A corresponds to Q, B corresponds to R, C corresponds to P.Hence, (B) ΔCBA ≅ ΔPRQ
Hence, option (b) is the correct answer.
Q.3. In Δ ABC, AB = AC and ∠B = 50°. Then ∠C is equal to
(a) 40°
(b) 50°
(c) 80°
(d) 130°
Correct Answer is Option (b)
According to the question,
Δ ABC, AB = AC and ∠B = 50°.Since, AB = AC
Δ ABC is an isosceles triangle.
Hence, ∠B = ∠C
∠B = 50° (given)
⇒ ∠C = 50°
Hence, option B is the correct option.
Q.4. In Δ ABC, BC = AB and ∠B = 80°. Then ∠A is equal to
(a) 80°
(b) 40°
(c) 50°
(d) 100°
Correct Answer is Option (c)
Given: Δ ABC, BC = AB and ∠B = 80°Since, BC = AB
Δ ABC is an isosceles triangle.
Let, ∠C = ∠A = x
∠B = 80° (given)
We know that,
Using angle sum property,
Sum of interior angles of a triangle should be = 180o
∠A + ∠B + ∠C = 180°
⇒ x + 80° + x = 180°
⇒ 2x = 180° – 80°
⇒ 2x = 100°
⇒ x = 50°
Therefore, ∠C = ∠A = 50°
Hence, option C is the correct answer.
Q.5. In Δ PQR, ∠R = ∠P and QR = 4 cm and PR = 5 cm. Then the length of PQ is
(a) 4 cm
(b) 5 cm
(c) 2 cm
(d) 2.5 cm
Correct Answer is Option (a)
Given: ΔPQR, ∠R = ∠P and QR = 4 cm and PR = 5 cmSince, ∠R = ∠P
Δ PQR is an isosceles triangle.
Hence, PQ = QR
⇒ PQ = 4cm
Hence, option A is the correct answer.
Q.6. D is a point on the side BC of a ∆ ABC such that AD bisects ∠BAC. Then
(a) BD = CD
(b) BA > BD
(c) BD > BA
(d) CD > CA
Correct Answer is Option (b)Given- In ∆ ABC, AD is the angular bisector AD meets BC at the point D We know that AD is the bisector of ∠BAC∠BAD = ∠CAD In ∆ ACD, external angle is ∠ADC As the external angle of a triangle is greater than each internal opposite angle of the same triangle∠ADB = ∠DAC + ∠DCA Here ∠DAC = ∠BAD ∠ADB = ∠BAD + ∠DCA i.e. ∠ADC > ∠BADBA > BD Therefore, if D is a point on the side BC of a ∆ ABC such that AD bisects ∠BAC then BA > BD.So option B is true.Option A is true only when the triangle is equlateral or isosceles.Option C is false since Option B is true.option D is false since∠ADC > ∠BAD or ∠CADCorrect Answer is Option (b)
Given- In ∆ ABC, AD is the angular bisector
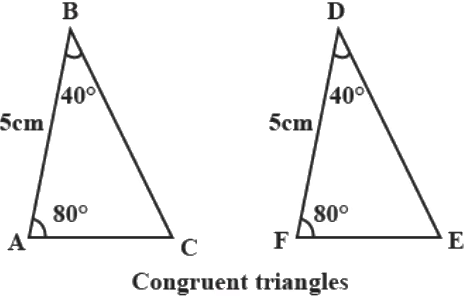
Q.7. It is given that ∆ ABC ≅ ∆ FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then which of the following is true?
(a) DF = 5 cm, ∠F = 60°
(b) DF = 5 cm, ∠E = 60°
(c) DE = 5 cm, ∠E = 60°
(d) DE = 5 cm, ∠D = 40°
Correct Answer is Option (b)Given:∆ ABC ≅ ∆ FDE, AB = 5 cm, ∠B = 40°, ∠A = 80° By c.p.c.t DF = AB So DF = 5 cm By c.p.c.t ∠E = ∠C Byangle sum property in ∆ ABC ∠A + ∠B + ∠C = 180° By substituting the values 80° + 40° + ∠C = 180° 120° + ∠C = 180° So we get ∠C = 180° - 120° ∠C = 60° So ∠E = ∠C = 60°Therefore, DF = 5 cm, ∠E = 60°is true.Therefore, DF = 5 cm, ∠E = 60° is true.
Q.8. Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be
(a) 3.6 cm
(b) 4.1 cm
(c) 3.8 cm
(d) 3.4 cm
Correct Answer is Option (d)
In a triangle, the difference between two sides should be less than the third side.
Hence, option d is correct 3.4 cm.
Q.9. In ∆ PQR, if ∠R > ∠Q, then
(a) QR > PR
(b) PQ > PR
(c) PQ < PR
(d) QR < PR
Correct Answer is Option (b) Given: In △PQR, ∠R > ∠Q As the sides opposite to greater angle is greater PQ > PR Therefore, PQ > PR .
Q.10. In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are
(a) isosceles but not congruent
(b) isosceles and congruent
(c) congruent but not isosceles
(d) neither congruent nor isosceles
Correct Answer is Option (a)
In △ABC and △PQR
∠C = ∠P (Given)
∠B = ∠Q (Given)
∠A = ∠R (Third angle of the triangle)
Thus, △ABC∼△PQR
Also, given, AB = AC
Thus, ∠B = ∠C (Isosceles triangle Property)
But, ∠B = ∠Q and ∠C = ∠P
Hence, ∠Q = ∠P
or PR = QR
Thus, both the triangles are Isosceles but not congruent.
Q.11. In triangles ABC and DEF, AB = FD and ∠A = ∠D. The two triangles will be congruent by SAS axiom if
(a) BC = EF
(b) AC = DE
(c) AC = EF
(d) BC = DE
Correct Answer is Option (b) In triangles ABC and DEF are It is given that AB = FD and ∠A = ∠D For a triangle to be congruent from the SAS axiom two sides and included angle must be equal For ∆ ABC ≅ ∆ DFE from SAS axiom we require AC = DE Therefore, the two triangles will be congruent by the SAS axiom if AC = DE.
Exercise 7.2 Page No: 65
Q.1. In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of Δ PQR should be equal to side AB of Δ ABC so that the two triangles are congruent? Give reason for your answer.
In triangle ABC and PQR, we have
∠A = ∠Q [Given]
∠B = ∠R [Given]
For the triangle to be congruent, AB should be equal to QR.
Hence, triangle ABC and PQR can be congruent by ASA congruence rule.
Q.2. In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of Δ PQR should be equal to side BC of Δ ABC so that the two triangles are congruent? Give reason for your answer.
In triangle ABC and PQR, we have
∠A = ∠Q and ∠B = ∠R [Given]
For the triangles to be congruent, we must have
BC = RP
Hence, triangle ABC and PQR will be congruent by AAS congruence rule.
Q.3. “If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
No, the statement, “if two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent” is false.
Justification:
Because by the congruent rule,
The two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle, i.e., SAS rule.
Q.4. “If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
The statement, “If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent.” is true.
Justification:
The statement is true because, the triangles will be congruent either by ASA rule or AAS rule. This is because two angles and one side are enough to construct two congruent triangles.
Q.5. Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.
No, it is not possible to construct a triangle with lengths of sides 4 cm, 3 cm and 7 cm.
Justification:
We know that,
Sum of any two sides of a triangle is always greater than the third side.
Here, the sum of two sides whose lengths are 4 cm and 3 cm = 4 cm + 3 cm = 7 cm,
Which is equal to the length of third side, i.e., 7 cm.
Hence, it is not possible to construct a triangle with lengths of sides 4 cm, 3 cm and 7 cm.
Q.6. It is given that Δ ABC ≅ Δ RPQ. Is it true to say that BC = QR? Why?
Ans: It is False Justification: Given ∆ ABC ≅ ∆ RPQ We know that AB = RP BC = PQ AC = RQ Here BC cannot be equal to QR Therefore, the statement is false.
Q.7. If ∆ PQR ≅ ∆ EDF, then is it true to say that PR = EF? Give reason for your answer.
Given: ∆ PQR ≅ ∆ EDF From the figure PQ = ED QR = DF PR = EF So PR = EF is true.Therefore, the statement is true.From the figure
Q.8. In ∆ PQR, ∠P = 70° and ∠R = 30°. Which side of this triangle is the longest? Give reason for your answer.
Given, △PQR, ∠P = 70°, ∠R = 30°
Sum of angles of triangle = 180°⇒ ∠P + ∠Q + ∠R = 180°
⇒ 70° + 30° + ∠Q = 180°
⇒ ∠Q = 80°
Since ∠Q is the largest ⇒ PR will be the longest side this is because when the two sides of a triangle are unequal, the angle opposite to the longer side is larger.
Q.9. AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2 AD? Give reason for your answer.
Given, △ABC, AD is median of triangle, on side BC
Now, In △ABD,AB + BD > AD (Sum of two sides of triangle is greater than the third side)
Now, In △ACD,
AC + CD > AD (Sum of two sides of triangle is greater than the third side)
Thus, adding both,
AB + BD + AC + CD > 2AD
AB + AC + BC > 2AD
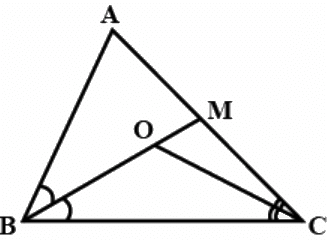
Q.10. M is a point on side BC of a triangle ABC such that AM is the bisector of ∠BAC. Is it true to say that perimeter of the triangle is greater than 2 AM? Give reason for your answer.
As long as point MM is on line BC,BC, the perimeter of △ABC △ABC would be greater than 2AM.2AM.
The sum of the two sides of a triangle is always greater that the third side.
In △ABM
AB + BM > AM ...(1)
In △ACM,
AC + CM > AM ...(2)
Now, adding equation (1) and (2),
AB + BM + AC + CM > AM + AM
AB + AC + BC > 2AM
Hence, the perimeter of △ABC is greater than 2AM.
Q.11. Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
For a triangle to be possible with given three sides, sum of two sides of the triangle must be greater than the third side.
Here, 9 + 7 = 16 < 17
The sum of two sides is less than the third side. Hence, a triangle is not possible.
Q.12. Is it possible to construct a triangle with lengths of its sides as 8 cm, 7 cm and 4 cm? Give reason for your answer.
Yes. It is possible to construct a triangle with lengths of its sides 8 cm,7 cm and 4 cm because the sum of two sides of a triangle is greater than the third side.
Exercise 7.3 Page No: 67
Q.1. ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.
According to the question,
ΔABC is an isosceles triangle and AB = AC, BD and CE are two mediansFrom ΔABD and ΔACE,
AB = AC (given)
2 AE = 2 AD (as D and E are mid points)
So, AE = AD
∠A = ∠A (common)
Hence, ΔABD ≅ ΔACE (using SAS)
⇒ BD = CE (by CPCT)
Hence proved.
Q.2. In Fig.7.4, D and E are points on side BC of a Δ ABC such that BD = CE and AD = AE.
Show that Δ ABD ≅ Δ ACE.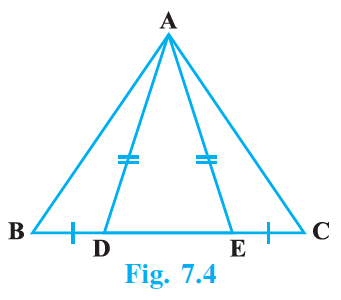
According to the question,
In ΔABC,
BD = CE and AD = AE.
In ΔADE,
AD = AE
Since opposite angles to equal sides are equal,
We have,
∠ADE = ∠AED … (1)
Now, ∠ADE + ∠ADB = 180° (linear pair)
∠ADB = 180° – ∠ADE … (2)
Also, ∠AED + ∠AEC = 180° (linear pair)
∠AEC = 180° – ∠AED
Since, ∠ADE = ∠AED
∠AEC = 180° – ∠ADE … (3)
From equation (2) and (3)
∠ADB = ∠AEC … (4)
Now, In ΔADB and ΔAEC,
AD = AE (given)
BD = EC (given)
∠ADB = ∠AEC (from (4)
Hence, ΔABD ≅ΔACE (by SAS)
Q.3. CDE is an equilateral triangle formed on a side CD of a square ABCD (Fig.7.5). Show that
ΔADE ≅ ΔBCE.
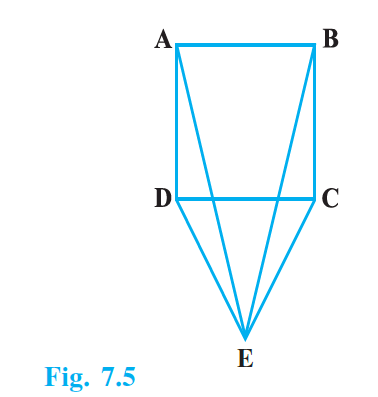
According to the question,
CDE is an equilateral triangle formed on a side CD of a square ABCD.
In ΔADE and ΔBCE,
DE = CE (sides of equilateral triangle)
Now,
∠ADC = ∠BCD = 90°
And, ∠EDC = ∠ECD = 60°
Hence, ∠ADE = ∠ADC + ∠CDE = 90° + 60° = 150°
And ∠BCE = ∠BCD + ∠ECD = 90° + 60° = 150°
⇒ ∠ADE = ∠BCE
AD = BC (sides of square)
Hence, ΔADE ≅ΔBCE (by SAS)
Q.4. In Fig.7.6, BA ⊥ AC, DE ⊥ DF such that BA = DE and BF = EC. Show that Δ ABC ≅ Δ DEF.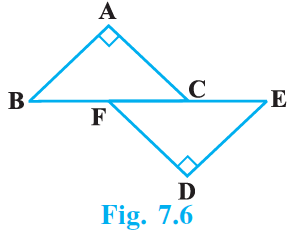
According to the question,
BA ⊥ AC, DE ⊥ DF such that BA = DE and BF = EC.
In ΔABC and ΔDEF
BA = DE (given)
BF = EC (given)
∠A = ∠D (both 90°)
BC = BF + FC
EF = EC + FC = BF + FC (∵ EC = BF)
⇒ EF = BC
Hence, ΔABC ≅ ΔDEF (by RHS)
Q.5. Q is a point on the side SR of a Δ PSR such that PQ = PR. Prove that PS > PQ.
Given: in ΔPSR, Q is a point on the side SR such that PQ = PR.
In ΔPRQ,
PR = PQ (given)
⇒ ∠PRQ = ∠PQR (opposite angles to equal sides are equal)
But ∠PQR > ∠PSR (exterior angle of a triangle is greater than each of opposite interior angle)
⇒ ∠PRQ > ∠PSR
⇒ PS > PR (opposite sides to greater angle is greater)
⇒ PS > PQ (as PR = PQ)
Q.6. S is any point on side QR of a ∆ PQR. Show that: PQ + QR + RP > 2 PS.
Theorem: In a triangle , sum of the length of any two sides is greater than the third side.
Draw the triangle and join the points P and S
In the figure,
In ΔPQS, according to the theorem,
PQ + QS > PS ...(1)
In ΔPSR, according to the theorem,
PR + SR > PS ... (2)
Adding (1) and (2),
PQ + QS + SR + PR > PS + PS
PQ + (QS + SR) + PR > 2PS
PQ + QR + PR > 2PS
Q.7. D is any point on side AC of a ∆ ABC with AB = AC. Show that CD < BD.
Consider the diagram shown below.
Given:
AB = AC
To prove:
CD < BD
Proof:
∠ABC = ∠ACB (Isosceles Triangle) … (1)
Here,
∠ABC = ∠CBD+∠DBA
∴∠ABC>∠CBD
Also, ⇒∠ACB=∠DCB>∠CBD {Because ∠ABC = ∠DCB = ∠ACB}
Therefore,
CD < BD (Converse of Angle opposite to greater side is greater in a triangle)
Hence, proved.
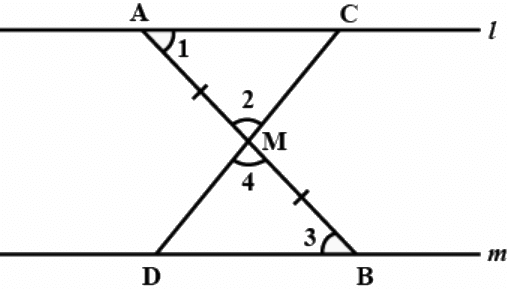
Q.8. In Fig. 7.7, l || m and M is the mid-point of a line segment AB. Show that M is also the mid-point of any line segment CD, having its end points on l and m, respectively.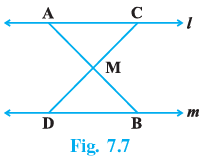
In △ AMC and △ BMD, we have
∠1 = ∠3 [Alt. ∠s because l ∥ m]
∠2 = ∠4 [Vert. opp. ∠s]
AM = BM [Given]
∴ △ AMC ≅ △ BMD [By ASS congruence rule]
∴ CM = DM [CPCT]
Hence, M is also the mid-point of CD.
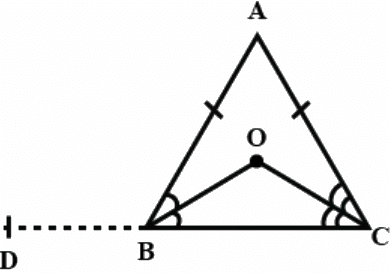
Q.9. Bisectors of the angles B and C of an isosceles triangle with AB = AC intersect each other at O. BO is produced to a point M. Prove that ∠MOC = ∠ABC.
Given:
Lines OB and OC are the bisectors of ∠B and ∠C of an isosceles ΔABC such that AB=AC which intersect each other at O and BO is produced to M.
To prove:
∠MOC = ∠ABC
Consider the diagram shown below.
Proof:
In ΔABC,
AB = AC (given)
∠ACB = ∠ABC (angles opposite to equal sides are equal)
(1/2) ∠ACB= (1/2) ∠ABC (dividing both sides by 2)
Therefore,
∠OCB = ∠OBC … (1)
(Since, OB and OC are the bisector of ∠B and ∠C)
Now, from equation (1), we have
∠MOC = ∠OBC + ∠OCB ∵ sum of interior angle = Exterior angle
∠MOC = 2∠OBC
⇒ ∠MOC = 2∠ABC × (1/2) = ∠ABC
(Since, OB is the bisector of ∠B)
Hence, proved.
Q.10. Bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Show that external angle adjacent to ∠ABC is equal to ∠BOC.
Given BD is Bisector of ∠ABC and CO is Bisector of ∠ACB produce CB to D
In ΔABC
AB=AC
∠ACB=∠ABC
(1/2)∠ACB = (1/2) ∠ABC
∠OCB = ∠OBC in ΔBOC∠OBC + ∠OCB + ∠BDC = 180°
2∠OBC+∠BOC=180°
∠ABC+∠BOC=180°
∠ABC+∠OBA=180°
∠DBA=∠BOC
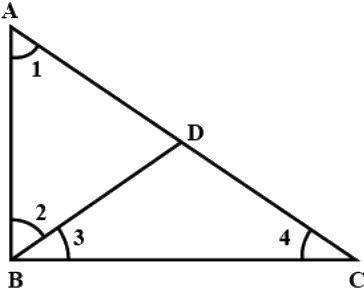
Q.11. In Fig. 7.8, AD is the bisector of ∠BAC. Prove that AB > BD.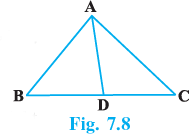
In ΔABC
AD is the bisector of ∠BAC
∠1 = ∠2 …(i)
Also in ΔADC
∠3 = ∠2 + ∠C (ext. angle is equal to sum of opposite interior angles)
∠3 > ∠2 (ext. angle is greater than one of the interior angles)
But ∠1 = ∠2
∠3 > ∠1
AB > BD
Hence proved.
Exercise 7.4 Page No: 69
Q.1. Find all the angles of an equilateral triangle.
In equilateral triangle,
All the sides are equal.
Therefore, all angles are also equal
Let the angles of an equilateral triangle = x
According to angle sum property,
We know that the sum of the interior angles is equal to 180o.
x + x + x =180o
3x = 180
x = 60°
Therefore, all the angles of an equilateral triangle are 60°
Q.2. The image of an object placed at a point A before a plane mirror LM is seen at the point B by an observer at D as shown in Fig. 7.12. Prove that the image is as far behind the mirror as the object is in front of the mirror.
[Hint: CN is normal to the mirror. Also, angle of incidence = angle of reflection].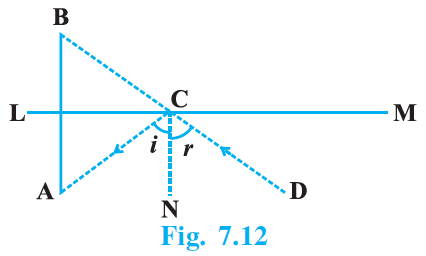
Let AB intersect LM at O. We have to prove that AO = BO.
Now, ∠i = ∠r …(1)
[∵ Angle of incidence = Angle of reflection]
∠B = ∠i [Corresponding angles] …(2)
And ∠A = ∠r [Alternate interior angles] …(3)
From (1), (2) and (3), we get
∠B = ∠A
⇒ ∠BCO = ∠ACO
In ΔBOC and ΔAOC we have
∠1 = ∠2 [Each = 90o]
OC = OC [Common side]
And ∠BCO = ∠ACO [Proved above]
ΔBOC ≅ ΔAOC [ASA congruence rule]
Hence, AO = BO [CPCT]
Q.3. ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Fig. 7.13). To prove that ∠BAD = ∠CAD, a student proceeded as follows:
In Δ ABD and Δ ACD,
AB = AC (Given)
∠B = ∠C (because AB = AC)
And ∠ADB = ∠ADC
Therefore, Δ ABD Δ Δ ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)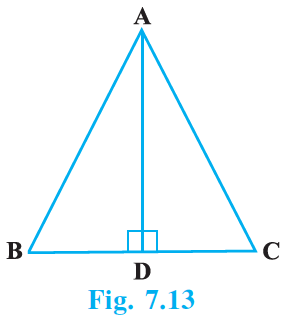 What is the defect in the above arguments?
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
In Δ ABD and Δ ADC, we have
∠ADB = ∠ADC
According to the question,
AB = BC
AD = AD [Common side]
By RHS criterion of congruence,
We have,
Δ ABD ≅ Δ ACD
∠BAD = ∠CAD [CPCT]
Hence Proved.
Q.4. P is a point on the bisector of ∠ABC. If the line through P, parallel to BA meet BC at Q, prove that BPQ is an isosceles triangle.
To prove: BPQ is an isosceles triangle.
According to the question,
Since, BP is the bisector of ∠ABC,
∠1 = ∠2 … (1)
Now, PQ is parallel to BA and BP cuts them
∠1 = ∠3 [Alternate angles] … (2)
From equations, (1) and (2),
We get
∠2 = ∠3
In Δ BPQ,
We have
∠2 = ∠3
PQ = BQ
Hence, BPQ is an isosceles triangle.
Q.5. ABCD is a quadrilateral in which AB = BC and AD = CD. Show that BD bisects both the angles ABC and ADC.
According to the question,
In ΔABC and ΔCBD,
We have
AB = BC
AD = CD
BD = BD [Common side]
ΔABC ≅ ΔCBD [By SSS congruence rule]
⇒ ∠1 = ∠2 [CPCT]
And ∠3 = ∠4
Hence, BD bisects both ∠ABC and ∠ADC.
Q.6. ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2 AD.
Given: A right angles triangle with AB = AC bisector of ∠A meets BC at D.
To prove: BC = 2ADProof:
According to the question,
In right Δ ABC,
AB = AC
Since, hypotenuse is the longest side,
BC is hypotenuse
∠BAC = 90o
Now,
In Δ CAD and Δ BAD,
We have,
AC = AB
Since, AD is the bisector of ∠A,
∠1 = ∠2
AD = AD [Common side]
Now,
By SAS criterion of congruence,
We get,
Δ CAD ≅ Δ BAD
CD = BD [CPCT]
Since, Mid-point of hypotenuse of a right triangle is equidistant from the 3 vertices of a triangle.
AB = BD = CD …(1)
Now, BC = BD + CD
⇒ BC = AD + AD [Using eq.(1)]
⇒ BC = 2AD
Hence, proved.
Q.7. O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that Δ OCD is an isosceles triangle.
According to the question,
It is given that: A square ABCD and OA = OB = AB.To prove: Δ OCD is an isosceles triangle.
Proof:
In square ABCD,
Since ∠1 and ∠2 is equal to 90o
∠1 = ∠2 …(1)
Now, in Δ OAB , we have
Since ∠3 and ∠4 is equal to 60o
∠3 = ∠4 …(2)
Subtracting equations (2) from (1),
We get
∠1−∠3 = ∠2 −∠4
⇒ ∠5 = ∠6
Now,
In Δ DAO and Δ CBO,
AD = BC [Given]
∠5 = ∠6 [Proved above]
OA = OB [Given]
By SAS criterion of congruence,
We have
Δ DAO ≅ Δ CBO
OD = OC
⇒ Δ OCD is an isosceles triangle.
Hence, proved.
Q.8. ABC and DBC are two triangles on the same base BC such that A and D lie on the opposite sides of BC, AB = AC and DB = DC. Show that AD is the perpendicular bisector of BC.
Given: Δ ABC and Δ DBC on the same base BC. Also, AB = AC and BD = DC.
To prove: AD is the perpendicular bisector of BC i.e., OB = OC
Proof: In Δ BAD and Δ CAD we have
AB = AC [Given]
BD = CD [Given]
AD = AD [common side]
So, by SSS criterion of congruence, we have
Δ BAD ≅ Δ CAD
∠1 = ∠2 [CPCT]
Now, in Δ BAO and Δ CAO, we have
AB = AC [Given]
∠1 = ∠2 [Proved above]
AO = AO [Common side]
So, by SAS criterion of congruence, we have
Δ BAO ≅ Δ CAO
BO = CO [CPCT]
And, ∠3 = ∠4 [CPCT]
But, ∠3+∠4 =180o [Linear pair axiom]
⇒ ∠3+∠3 =180
⇒ 2∠3 =180
⇒ ∠3 =180/2
⇒ ∠3 = 90o
Since BO = CO and ∠3 = 90o,
AD is perpendicular bisector of BC.
Hence, proved.
Q.9. ABC is an isosceles triangle in which AC = BC. AD and BE are respectively two altitudes to sides BC and AC. Prove that AE = BD.
According to the question,
In Δ ADC and Δ BEC,
We have
AC = BC [Given] …(1)
Since ∠ADC and ∠BEC = 90o
∠ADC = ∠BEC
∠ACD = ∠BCE [Common angle]
Δ ADC ≅ Δ BEC [By ASA congruence rule]
CE = CD … (2) [CPCT]
Subtracting equation (2) from (1),
We get
AC – CE = BC – CD
⇒ AE = BD
Hence, proved.
Q.10. Prove that sum of any two sides of a triangle is greater than twice the median with respect to the third side.
According to the question,
We have, Δ ABC with median AD.
To prove:
AB + AC > 2AD
AB + BC > 2AD
BC + AC > 2AD
Construction:
Extend AD to E such that DE = AD
Join EC.
Proof:
In Δ ADB and Δ EDC,
AD = ED [By construction]
∠1 = ∠2 [Vertically opposite angles are equal]
DB = DC [Given]
So, by SAS criterion of congruence, we have
Δ ADB ≅ Δ EDC
AB = EC [CPCT]
And ∠3 = ∠4 [CPCT]
Now, in Δ AEC,
Since sum of the lengths of any two sides of a triangle must be greater than the third side,
We have
AC + CE > AE
⇒ AC + CE > AD + DE
⇒ AC +CE > AD+ AD [\AD = DE]
⇒ AC + CE > 2AD
⇒ AC + AB > 2AD [∵AB = CE]
Similarly,
We get,
AB + BC > 2AD and BC + AC >2AD.
Hence, proved.
Q.11. Show that in a quadrilateral ABCD, AB + BC + CD + DA < 2 (BD + AC)
Since, the sum of lengths of any two sides in a triangle should be greater than the length of third side
Therefore,
In Δ AOB, AB < OA + OB ...(i)
In Δ BOC, BC < OB + OC ...(ii)
In Δ COD, CD < OC + OD ...(iii)
In Δ AOD, DA < OD + OA ...(iv)
⇒ AB + BC + CD + DA < 2OA + 2OB + 2OC + 2OD
⇒ AB + BC + CD + DA < 2[(AO + OC) + (DO + OB)]
⇒ AB + BC + CD + DA < 2(AC + BD)
Hence, it is proved.
Q.12. Show that in a quadrilateral ABCD, AB + BC + CD + DA > AC + BD?
ABCD is a quadrilateral and AC, and BD are the diagonals.
Sum of the two sides of a triangle is greater than the third side.
So, considering the triangle ABC, BCD, CAD and BAD, we get
AB + BC > AC
CD + AD > AC
AB + AD > BD
BC + CD > BD
Adding all the above equations,
2(AB + BC + CA + AD) > 2(AC + BD)
⇒ 2(AB + BC + CA + AD) > 2(AC + BD)
⇒ (AB + BC + CA + AD) > (AC + BD)
Hence, Proved.
Q.13. In a triangle ABC, D is the mid-point of side AC such that BD = (1/2) AC. Show that ∠ABC is a right angle.
D is mid-point of AC
AD = DC = (1/2)AC
But BD = (1/2) AC (given)
AD = DC = BD
In ΔABD
AD = BD
∠2 = ∠1 = x (angles opposite to equal sides are equal)
Also BD = DC
∠3 = ∠4 = x
In ΔABC
∠1 + (∠2 + ∠3) + ∠4 = 180°
x + (x+x) + x = 180°
4x = 180°
x = 45°
∠ABC= x + x = 45° + 45° = 90°
Hence proved.
Q.14. In a right triangle, prove that the line-segment joining the mid-point of the hypotenuse to the opposite vertex is half the hypotenuse.
Let P be the mid point of the hypotenuse of the right △ABC right angled at B
Draw a line parallel to BC from P meeting B at O
Join PB
In △PAD and △PBD
∠PDA = ∠PDB 90° each due to conv of mid point theorem
PD = PD ....... (common)
AD = DB ...... (As D is mid point of AB)
So △ PAD and PBD are congruent by SAS rule
PA = PB ...... (C.P.C.T)
As PA = PC .... (Given as P is mid-point)
∴ PA = PC = PB
Q.15. Two lines l and m intersect at the point O and P is a point on a line n passing through the point O such that P is equidistant from l and m. Prove that n is the bisector of the angle formed by l and m.
Given: Lines, l and m and n intersect at point O,P is a point on line n and such that P is equidistant from l and n.
Refer image,
To prove: n us the bisector of ∠QOR
Proof: In ΔOQP and ΔORP, we have ∠1 = ∠2
[∵ Each equal to 90°]
OP = OP [Common side]
PQ = QR [Given]
So, by RHS criterion of congruence, we have
ΔOQP ≅ ΔORP
∴∠3 = ∠4 [CPCT]
So, n is bisector of ∠QOR
Hence, proved.
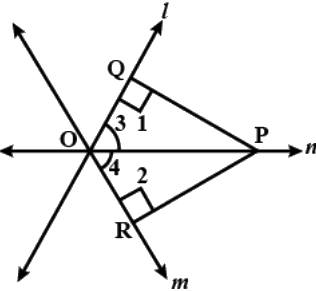
Q.16. Line segment joining the mid-points M and N of parallel sides AB and DC, respectively of a trapezium ABCD is perpendicular to both the sides AB and DC. Prove that AD = BC.
Construct AN and BN at the point N
Consider △ANM and ∠BNM
We know that N is the midpoint of the line AB
So we get
AM = BM
From the figure we know that
∠AMN = ∠BMN = 90°
MN is common i.e. MN = MN
By SAS congruence criterion
△ANM ≅ △BNM
AN = BN(c.p.c.t) …(1)
We know that
∠ANM = ∠BNM(c.p.c.t)
Subtracting LHS and RHS by 90°
90° − ∠ANM = 90°− ∠BNM
So we get
∠AND = ∠BNC …(2)
Now, consider △AND and △BNC
AN = BN
∠AND = ∠BNC
We know that N is the midpoint of the line DC
DN = CN
By SAS congruence criterion
△AND ≅ △BNC
AD = BC(c.p.c.t)
Therefore, it is proved that AD = BC.
Q.17. ABCD is a quadrilateral such that diagonal AC bisects the angles A and C. Prove that AB = AD and CB = CD.
In ΔABC and ΔADC,
∠BAC = ∠DAC (given)
∠ACB = ∠ACD (given)
AC = AC (common)
∴ ΔABC ≅ ΔADC (ASA axiom)
∴ AB = AD and CB = CD by CPCT.
Q.18. ABC is a right triangle such that AB = AC and bisector of angle C intersects the side AB at D. Prove that AC + AD = BC.
Let AB = AC = a and AD = b.△ABC is right angled at A ⇒ AB2 + AC2 = BC2 ⇒ BC = a√2BD = AB − AD = a−bBy angle-bisector theorem, ⇒ a + b = a√2But, we know AC= a, AD = b, BC = a√2⇒ AC + AD = BC. Hence it is proved.Let AB = AC = a and AD = b.
△ABC is right angled at A ⇒ AB2 + AC2 = BC2 ⇒ BC = a√2
BD = AB − AD = a−b
By angle-bisector theorem,
⇒ a + b = a√2
But, we know AC= a, AD = b, BC = a√2
⇒ AC + AD = BC. Hence it is proved.
Q.19. AB and CD are the smallest and largest sides of a quadrilateral ABCD. Out of ∠B and ∠D decide which is greater.
Let ABCD be a quadrilateral such that AB is it's smallest side and CD is it largest side.
Now join AC and BD
In ΔABC ,we have
BC > AB
⇒ ∠8 > ∠3 ...(1) {∵ angle opposite to longer side is greater.}
Since CD is the longest side of quadrilateral ABCD
In ΔACD, we have
CD > AD
⇒ ∠7 > ∠4 ...(2)
Adding (1) and(2) we get
∠8 + ∠7 > ∠3 + ∠4
⇒ ∠A > ∠C
Now in ΔABD, we have
AD > AB {∵ AB is the shortest side}
⇒ ∠1 > ∠6 ...(3)
In ΔBCD,we have
CD > BC
⇒ ∠2 > ∠5 ....(4)
Adding (3) and (4)
∠1 + ∠2 > ∠5 + ∠6
⇒ ∠B > ∠D
Hence proved.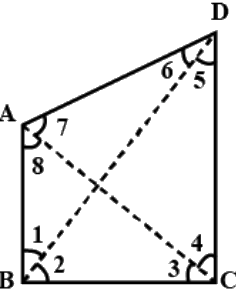
Q.20. Prove that in a triangle, other than an equilateral triangle, angle opposite the longest side is greater than (2/3) of a right angle.
Consider △PQR where PR is the longest side
So we get PR > PQ
i.e. ∠Q > ∠R ...(1)
We also know that PR > QR
i.e. ∠Q > ∠P ...(2)
By adding both the equations
∠Q + ∠Q > ∠R + ∠P
So we get
2 ∠Q > ∠R + ∠P
By adding ∠Q on both LHS and RHS
2∠Q + ∠Q > ∠R + ∠P + ∠Q
We know that ∠R + ∠P + ∠Q = 180°
So we get
3 ∠ Q > 180°
By division
∠Q > 60°
So we get
∠Q > (2/3)(90°)
i.e. ∠Q > (2/3)of a right angle
Therefore, it is proved that in a triangle, other than an equilateral triangle, angle opposite the longest side is greater (2/3) of a right angle.
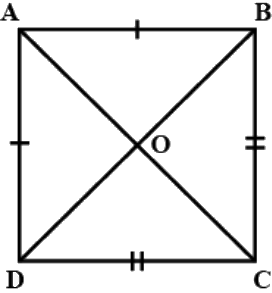
Q.21. ABCD is quadrilateral such that AB = AD and CB = CD. Prove that AC is the perpendicular bisector of BD.
In △AOB and △AOD
AB = AD (given)
∠BAD = ∠DAO (AC bisects ∠A)
∴AO = AO [common]
⇒ △AOB ≅ △AOD [SAS]
DO = BO ...(i) [CPCT]
∠AOD = ∠AOB
∠AOD + ∠AOB=180°
⇒ ∠AOD = ∠AOB = 90° ...(ii)
From (i) and (ii)
AC is perpendicular bisector of BD
|
40 videos|471 docs|57 tests
|
FAQs on NCERT Exemplar Solutions: Triangles - Mathematics (Maths) Class 9
| 1. What is a triangle and what are its key properties? |  |
| 2. How can the area of a triangle be calculated? |  |
| 3. What is the significance of the Pythagorean theorem in triangles? |  |
| 4. How do you determine if three lengths can form a triangle? |  |
| 5. What are the different types of triangles based on their angles? |  |