NCERT Exemplar: Statistics | Mathematics (Maths) Class 11 - Commerce PDF Download
SHORT ANSWER TYPE QUESTION
Q.1. Find the mean deviation about the mean of the distribution:
Ans.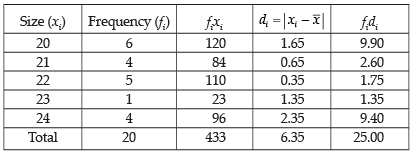
Mean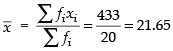
Mean deviation MD =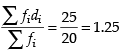
Here, the required MD = 1.25
Q.2. Find the mean deviation about the median of the following distribution:
Ans.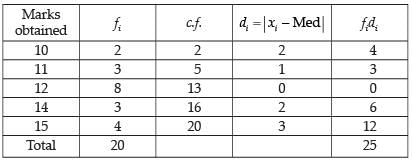
Here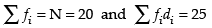
Median = 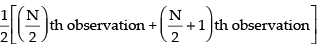
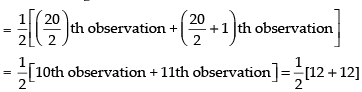
∴ Median = 12
∴ 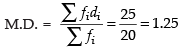
Hence, the required MD = 1.25
Q.3. Calculate the mean deviation about the mean of the set of first n natural numbers when n is an odd number.
Ans.
First n natural numbers are 1, 2, 3, ..., n. Here, n is odd.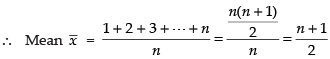
The deviations of numbers from mean 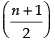 are
are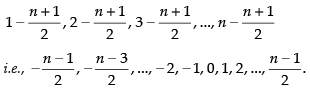
The absolute values of deviation from the mean i.e.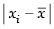 are
are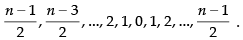
The sum of absolute values of deviations from the mean i.e.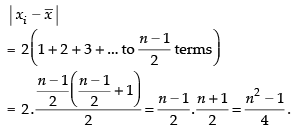
∴ Mean deviation about the mean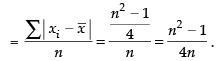
Q.4. Calculate the mean deviation about the mean of the set of first n natural numbers when n is an even number.
Ans. First n natural numbers are 1, 2, 3, 4, 5, 6, …, n (even)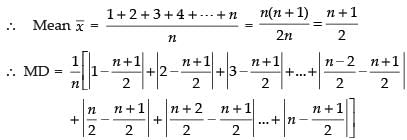

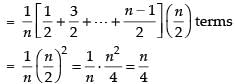
[∴ Sum of first odd n natural numbers = n2]
Hence, the required MD = n/4.
Q.5. Find the standard deviation of the first n natural numbers.
Ans.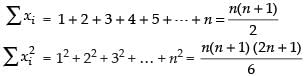
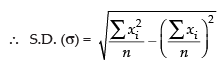
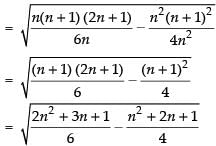
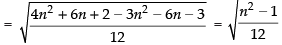
Hence, the required SD =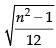
Q.6. The mean and standard deviation of some data for the time taken to complete a test are calculated with the following results:
Number of observations = 25, mean = 18.2 seconds, standard deviation = 3.25 seconds.
Further, another set of 15 observations x1, x2, ..., x15, also in seconds, is now available and we have 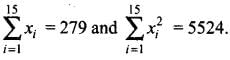 Calculate the standard derivation based on all 40 observations.
Calculate the standard derivation based on all 40 observations.
Ans. Given that n1 = 25, 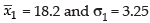
and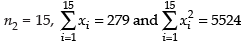
For the first set, we have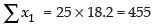
∴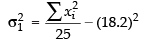
⇒ 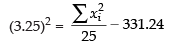
⇒ 10.5625 + 331.24 =
For the combined standard deviation of the 40 observation, n = 40
and
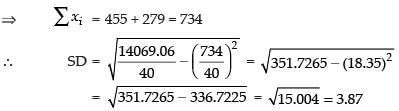
Hence, the required SD = 3.87
Q.7. The mean and standard deviation of a set of n1 observations are 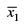 and s1, respectively while the mean and standard deviation of another set of n2 observations are
and s1, respectively while the mean and standard deviation of another set of n2 observations are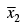 and s2, respectively. Show that the standard deviation of the combined set of (n1 + n2) observations is given by
and s2, respectively. Show that the standard deviation of the combined set of (n1 + n2) observations is given by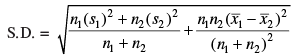
Ans.
Let xi, i = 1, 2, 3, 4, …, n1
and yj, j = 1, 2, 3, 4, …, n2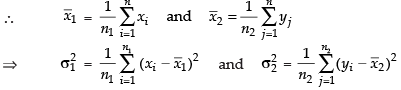
Now mean of the combined series is given by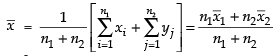
Therefore, σ2 of the combined series is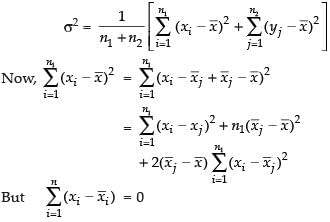
[∴ The algebraic sum of the deviation of values of first series from their mean is zero]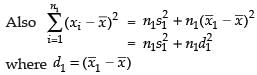
Similarly, we have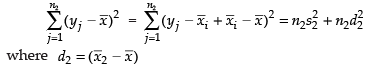
Now combined Standard Deviation (SD)
Q.8. Two sets each of 20 observations, have the same standard derivation 5. The first set has a mean 17 and the second a mean 22. Determine the standard deviation of the set obtained by combining the given two sets.
Ans.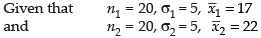
Now we know for combined two series that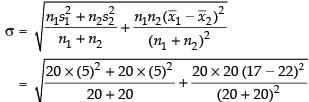
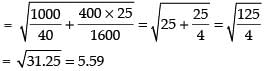
Hence, the required SD = 5.59
Q.9. The frequency distribution: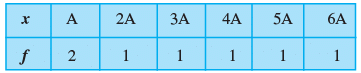
where A is a positive integer, has a variance of 160. Determine the value of A.
Ans.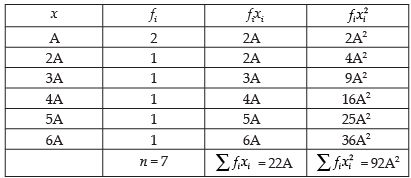
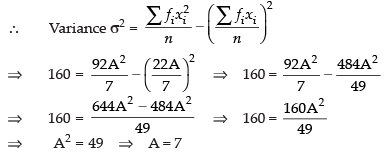
Hence, the value of A is 7.
Q.10. For the frequency distribution: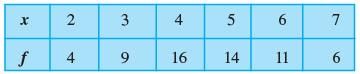
Find the standard distribution.
Ans.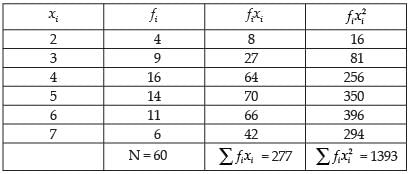
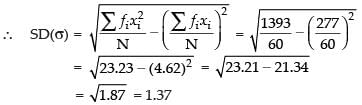
Hence, the required SD = 1.37
Q.11. There are 60 students in a class. The following is the frequency distribution of the marks obtained by the students in a test:
where x is a positive integer. Determine the mean and standard deviation of the marks.
Ans. Given that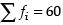
∴ x – 2 + x + x2 + (x + 1)2 + 2x + (x + 1) = 60
⇒ 4x – 2 + x2 + x2 + 2x + 1 + x + 1 = 60
⇒ 2x2 + 7x – 60 = 0
⇒ 2x2 + 15x – 8x – 60 = 0
⇒ x(2x + 15) – 4(2x + 15) = 0
⇒ (2x + 15) (x – 4) = 0
⇒ 2x + 15 = 0
∴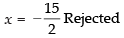
∴ x = 4 [∴ x ∈ I+]
Now put x = 4 in the frequency distribution table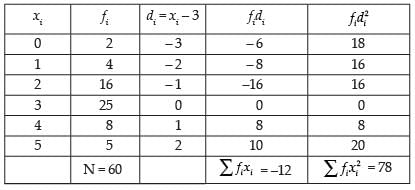
Let assumed mean A = 3
and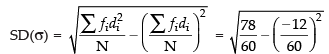
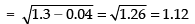
Hence, the required mean = 2.8 and SD = 1.12
Q.12. The mean life of a sample of 60 bulbs was 650 hours and the standard deviation was 8 hours. A second sample of 80 bulbs has a mean life of 660 hours and standard deviation 7 hours. Find the overall standard deviation.
Ans.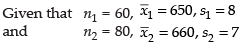
we know that for a combined series.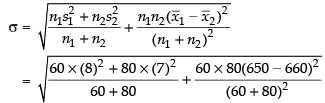
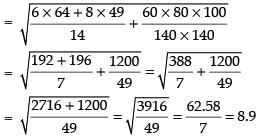
Hence, the required SD = 8.9
Q.13. Mean and standard deviation of 100 items are 50 and 4, respectively. Find the sum of all the item and the sum of the squares of the items.
Ans.
Given that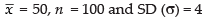
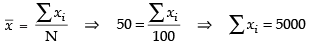
and variance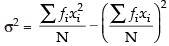
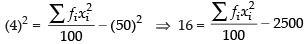
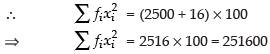
Hence, the required sum are 5000 and 251600.
Q.14. If for a distribution ∑(x − 5) = 3, ∑(x − 5)2 = 43 and the total number of item is 18, find the mean and standard deviation.
Ans.
Given that 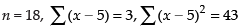
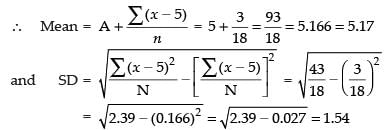
Hence, the required mean is 5.17 and SD = 1.54
Q.15. Find the mean and variance of the frequency distribution given below:
Ans.
Mean =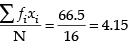
Variance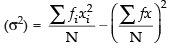
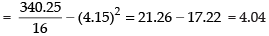
Hence, the required mean = 4.15 and variance = 4.04
LONG ANSWER TYPE QUESTION
Q.16. Calculate the mean deviation about the mean for the following frequency distribution:
Ans.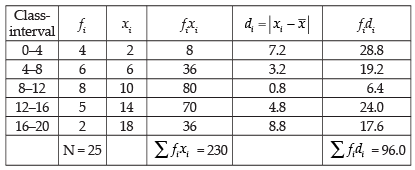
Mean =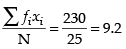
and Mean deviation =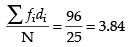
Hence, the required MD = 3.84
Q.17. Calculate the mean deviation from the median of the following data:
Ans.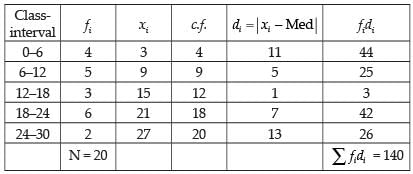
Median class =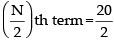 th term 10th term i.e.12 – 18
th term 10th term i.e.12 – 18
∴ Median =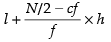
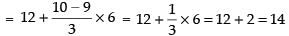
and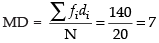
Hence, the required MD = 7
Q.18. Determine the mean and standard deviation for the following distribution:
Ans.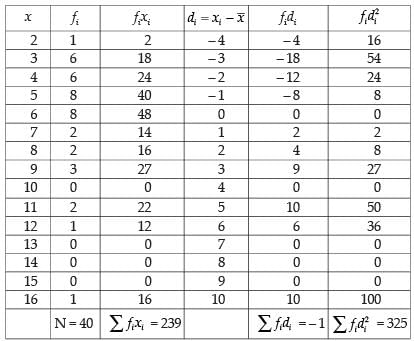
Mean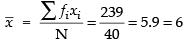
∴ 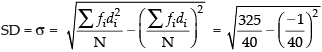
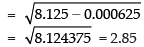
Here, the required mean = 6 and MD = 2.85
Q.19. The weights of coffee in 70 jars is shown in the following table:
Determine variance and standard deviation of the above distribution.
Ans.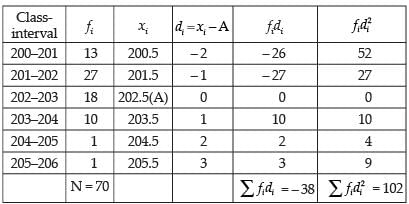
∴ Variance =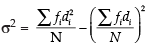
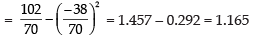
∴ 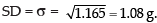
Hence, the required variance = 1.165 and SD = 1.08 g
Q.20. Determine mean and standard deviation of first n terms of an A.P. whose first term is a and common difference is d.
Ans.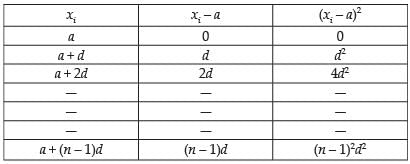
We know that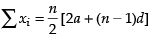
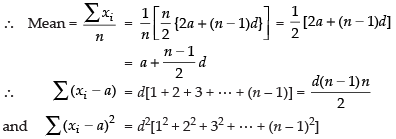
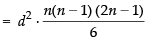
∴
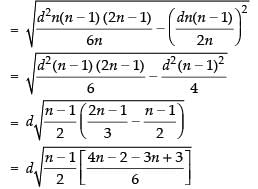
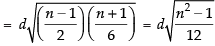
Hence, the required SD = 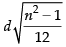
Q.21. Following are the marks obtained, out of 100, by two students Ravi and Hashina in 10 tests.
who is more intelligent and who is more consistent?
Ans.
Case I: For Ravi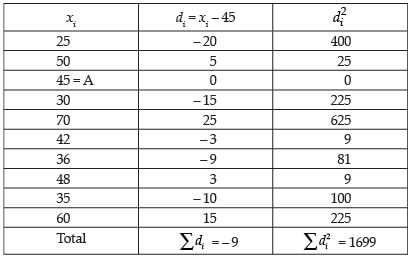
∴ 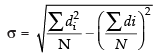
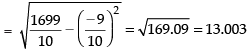
and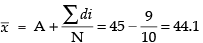
Now for Hashina
Assumed mean A = 55
∴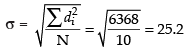

Hence, Hashina is more consistent and intelligent.
Q.22. Mean and standard deviation of 100 observations were found to be 40 and 10, respectively. If at the time of calculation two observations were wrongly taken as 30 and 70 in place of 3 and 27 respectively, find the correct standard deviation.
Ans.
Given that n = 100,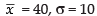
∴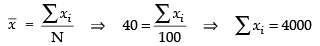
Corrected 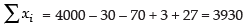
and Corrected mean =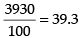
Now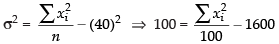
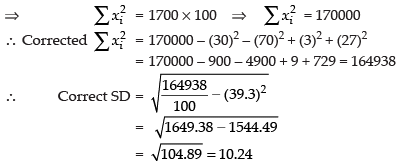
Hence, the required SD = 10.24.
Q.23. While calculating the mean and variance of 10 readings, a student wrongly used the reading 52 for the correct reading 25. He obtained the mean and variance as 45 and 16 respectively. Find the correct mean and the variance.
Ans. Given that n = 10,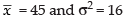
∴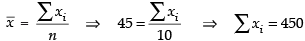
Corrected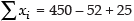
= 423
∴ Correct Mean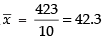
and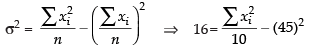
⇒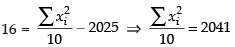
∴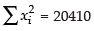
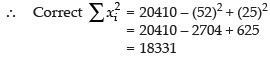
and corrected variance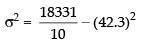
= 1833.1 – 1789.3 = 43.8
Hence the required mean = 42.3 and variance = 43.8
OBJECTIVE ANSWERS TYPE QUESTIONS
Q.24. The mean deviation of the data 3, 10, 10, 4, 7, 10, 5 from the mean is
(a) 2
(b) 2.57
(c) 3
(d) 3.75
Ans. (b)
Solution.
Observations are given by 3, 10, 10, 4, 7, 10 and 5
∴ 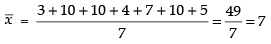
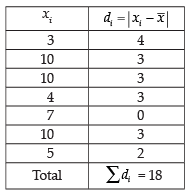
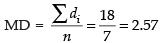
Hence, the correct option is (b).
Q.25. Mean deviation for n observations x1, x2, ..., xn from their mean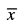
(a) 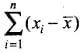
(b) 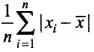
(c) 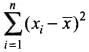
(d) 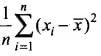
Ans. (b)
Solution.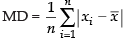
Hence, the correct option is (b).
Q.26. When tested the lines (in hours) of 5 bulbs were noted as follows:
1357, 1090, 1666, 1494, 1623
The mean deviation (in hours) from their mean is
(a) 178
(b) 179
(c) 220
(d) 356
Ans. (a)
Solution.
The lines of 5 bulbs are given by
1357, 1090, 1666, 1494, 1623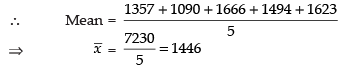
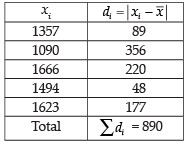
∴
Hence, the correct option is (a).
Q.27. Following are the marks obtained by 9 students in a Mathematics test
50, 69, 20, 33, 53, 39, 40, 65, 59.
The mean deviation from the median is
(a) 9
(b) 10.5
(c) 12.67
(d) 14.76
Ans. (c)
Solution.
Marks obtained are 50, 69, 20, 33, 53, 39, 40, 65 and 59
Let us write in ascending order
20, 33, 39, 40, 50, 53, 59, 65, 69.
Here n = 9
∴ Median =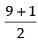 th term = 5th term i.e. 50
th term = 5th term i.e. 50
∴ Median = 50
Now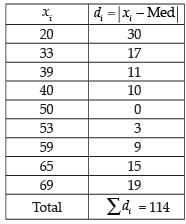
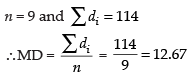
Hence, the correct option is (c).
Q.28. The standard deviation of the data 6, 5, 9, 13, 12, 8, 10 is
(a)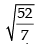
(b) 52/7
(c) √6
(d) 6
Ans. (a)
Solution.
Given data are 6, 5, 9, 13, 12, 8 and 10
∴ n = 7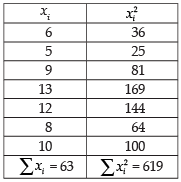
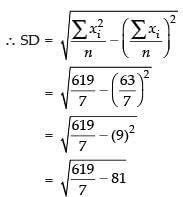
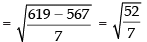
Hence, the correct option is (a).
Q.29. Let x1, x2, ..., xn be n observations and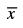 be their arithmetic mean. The formula for the standard deviation is given by
be their arithmetic mean. The formula for the standard deviation is given by
(a)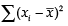
(b)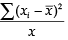
(c)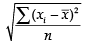
(d)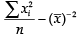
Ans. (c)
Solution.
The formula for S.D =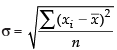
Hence, the correct option is (c).
Q.30. If the mean of 100 observations is 50 and their standard deviation is 5, then the sum of all the squares of all the observations is
(a) 50,000
(b) 250000
(c) 252500
(d) 255000
Ans. (c)
Solution.
Here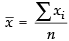
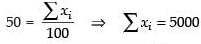
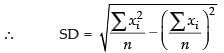
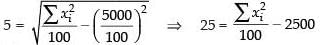
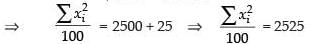
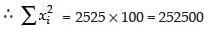
Hence, the correct option is (c).
Q.31. If a, b, c, d and e be the observations with mean m and standard deviations S, then find the standard deviation of the observations a + K, b + K, c + K, d + K and e + K is
(a) S
(b) KS
(c) S + K
(d) S/K
Ans. (a)
Solution.
Given observation are a, b, c, d and e
∴ Mean =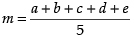
∴ 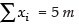
Now mean of a + K, b + K, c + K, d + K and e + K is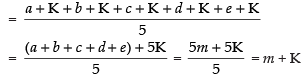
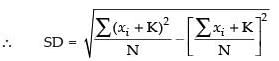
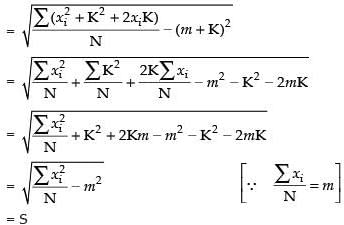
Hence, the correct option is (a).
Q.32. If x1, x2, x3, x4 and x5 be the observations with mean m and standard deviations S then, the standard deviation of the observations Kx1, Kx2, Kx3, Kx4 and Kx5 is
(a) K + S
(b) S/K
(c) KS
(d) S
Ans. (c)
Solution.
Here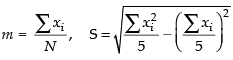
∴ 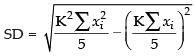
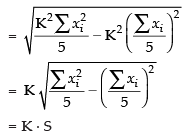
Here, the correct option is (c).
Q.33. Let x1, x2, x3, …, xn be n observations. Let wi = lxi + k for i = 1, 2, …, n where l and k are constants. If the mean of xi’s is 48 and their standard deviation is 12, the mean of wi’s is 55 and standard deviations of wi’s is 15, then the values of l and k should be
(a) l = 1.25, k = – 5
(b) l = – 1.25, k = 5
(c) l = 2.5, k = – 5
(d) l = 2.5, k = 5
Ans. (a)
Solution.
Given that wi = xi + k,
wi = 55 and SD(wi) = 15
then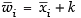
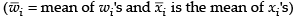
⇒ 55 = 48 + k (i)
SD of wi = SD of xi
15 = l x 12
⇒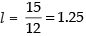 (ii)
(ii)
from eq. (i) and (ii) we have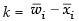 = 55 – 1.25 x 48 = 55 - 60 = 5
= 55 – 1.25 x 48 = 55 - 60 = 5
Here, the correct option is (a).
Q.34. The standard deviations for first 10 natural numbers is
(a) 5.5
(b) 3.87
(c) 2.97
(d) 2.87
Ans. (d)
Solution.
We know that SD of first n natural numbers
Here n = 10
∴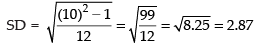
Hence, the correct option is (d).
Q.35. Consider the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10. If 1 is added to each numbers, the variance of the numbers, so obtained is
(a) 6.5
(b) 2.87
(c) 3.87
(d) 8.25
Ans. (d)
Solution.
Given numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Numbers obtained when 1 is added to the above numbers is
2, 3, 4, 5, 6, 7, 8, 9, 10 and 11.
∴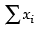 = 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11
= 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11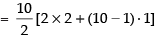
= 5[4 + 9] = 5 x 13 = 65
Now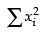 = 22 + 32 + 42 + ... + 112
= 22 + 32 + 42 + ... + 112
= (12 + 22 + 32 + 42 + ... + 112) - (1)2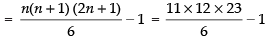
= 22 x 23 - 1 = 506 - 1 = 505
∴ Variance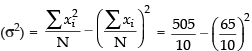
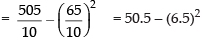
= 50.5 – 42.25 = 8.25
Hence, the correct option is (d).
Q.36. Consider the first 10 positive integers. If we multiply each number by – 1 and then add 1 to each number, the variance of the numbers, so obtained is (a) 8.25
(b) 6.5
(c) 3.85
(d) 2.87
Ans. (a)
Solution.
First 10 positive integers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
on multiplying each number by – 1, we get
– 1, – 2, – 3, – 4, – 5, – 6, – 7, – 8, – 9, – 10
on adding 1 to each of the number, we get
0, – 1, – 2, – 3, – 4, – 5, – 6, – 7, – 8, – 9
∴ 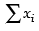 = 0 – 1 – 2 – 3 – 4 – 5 – 6 – 7 – 8 – 9
= 0 – 1 – 2 – 3 – 4 – 5 – 6 – 7 – 8 – 9
= – 45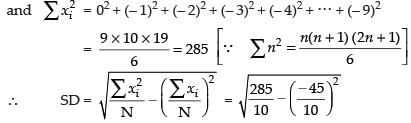
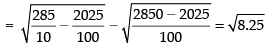
∴ Variance = (SD)2 =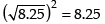
Hence, the correct option is (a).
Q.37. The following information relates to a sample of size 60 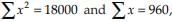 then the variance is
then the variance is
(a) 6.63
(b) 16
(c) 22
(d) 44
Ans. (d)
Solution.
We know that variance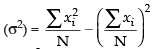
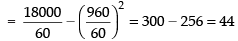
Hence, the correct option is (d).
Q.38. Coefficient of variation of two distributions are 50 and 60, and their arithmetic means are 30 and 25 respectively. Difference of their standard deviation is
(a) 0
(b) 1
(c) 1.5
(d) 2.5
Ans. (a)
Solution.
Here, we have CV1 = 50, CV2 = 60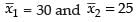
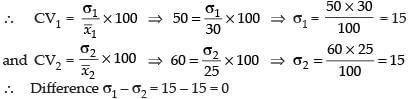
Hence, the correct option is (a).
Q.39. The standard deviation of some temperature data in °C is 5. If the data were converted into ºF, the variance would be
(a) 81
(b) 57
(c) 36
(d) 25
Ans. (a)
Solution.
Given that σC = 5
We know that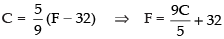
∴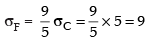
∴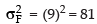
Hence, the correct option is (a)
FILL IN THE BLANKS
Q.40. Coefficient of variation =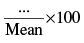
Ans.
Hence, the value of the filler is SD.
Q.41. If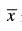 is the mean of n values of x, then
is the mean of n values of x, then 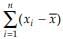 is always equal to _______. If a has any value other than
is always equal to _______. If a has any value other than 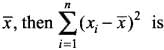 _________ than ∑(xi - a)2.
_________ than ∑(xi - a)2.
Ans. If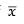 is the mean of n observations of x, then
is the mean of n observations of x, then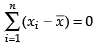 and if ‘a’ has the value other than
and if ‘a’ has the value other than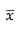 then
then 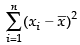 is less than
is less than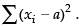
Hence, the value of the fillers are 0 and less.
Q.42. If the variance of a data is 121, then the standard deviation of the data
is _______.
Ans. We know that SD =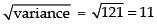
Hence, the value of the filler is 11.
Q.43. The standard deviation of a data is ___________ of any change in origin, but is _____ on the change of scale.
Ans. Since the standard deviation of any data is independent of any change in origin but is dependent of any change of scale.
Hence, the value of the fillers are independent and dependent.
Q.44. The sum of the squares of the deviations of the values of the variable is _______ when taken about their arithmetic mean.
Ans. The sum of the squares of the deviations of the value of variable is minimum when taken about their arithmetic mean.
Hence, the value of the filler is minimum.
Q.45. The mean deviation of the data is _______ when measured from the median.
Ans. The mean deviation of the data is least when measured from the median. Hence, the value of the filler is least.
Q.46. The standard deviation is _______ to the mean deviation taken from the arithmetic mean.
Ans. The standard deviations is greater than or equal to the mean deviation taken from the arithmetic mean.
Hence, the value of the filler is greater than or equal.
|
73 videos|264 docs|91 tests
|
FAQs on NCERT Exemplar: Statistics - Mathematics (Maths) Class 11 - Commerce
| 1. What is the importance of studying statistics? |  |
| 2. How can statistics be used to describe data? |  |
| 3. What are the different types of sampling techniques used in statistics? |  |
| 4. How do hypothesis testing and confidence intervals relate to statistics? |  |
| 5. Can statistics be used to analyze relationships between variables? |  |





















