NCERT Exemplar: Trigonometric Functions | Mathematics (Maths) for JEE Main & Advanced PDF Download
Q.1. Prove that 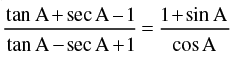
Ans.
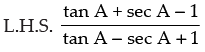
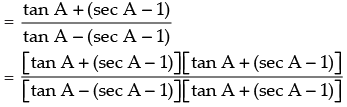
[Rationalizing the denominator]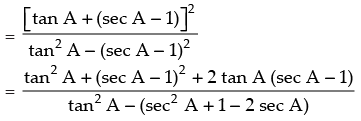
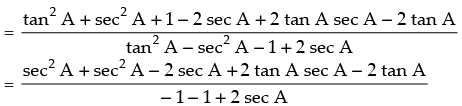
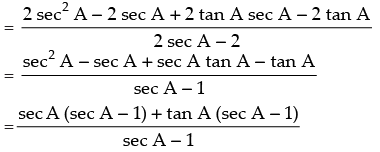
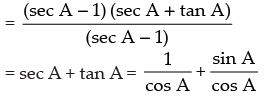
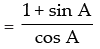 R.H.S. Hence proved.
R.H.S. Hence proved.
Q.2. If 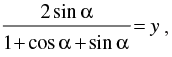 then prove that
then prove that
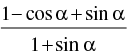 is also equal to y.
is also equal to y.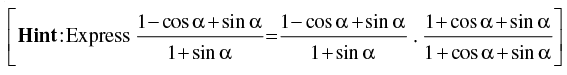
Ans.
Given that: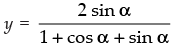
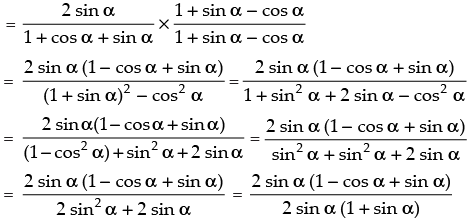
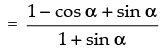
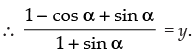
Hence proved.
Q.3. If m sin θ = n sin (θ + 2α), then prove that tan (θ + α) cot α = 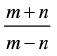
[Hint: Express 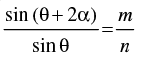 and apply componendo and dividendo]
and apply componendo and dividendo]
Ans.
Given that: m sin θ = n sin (θ + 2α)
⇒ 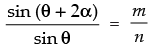
Using componendo and dividendo theorem we get
⇒ 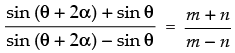
⇒ 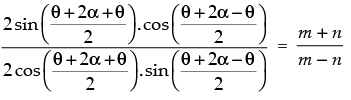
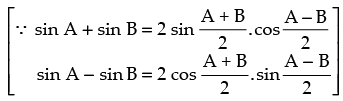
⇒ 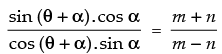
⇒ 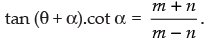
Hence proved.
Q.4. If cos (α + β) = 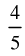 and sin (α – β) =
and sin (α – β) =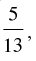 where α lie between 0 and
where α lie between 0 and 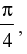 find the value of tan2α.
find the value of tan2α.
[Hint: Express tan 2 α as tan (α + β + α – β]
Ans.
Given that: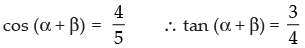
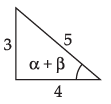
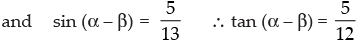
Now tan 2α = tan [α + β + α – β]
= tan [(α + β) + (α – β)]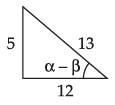
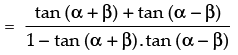
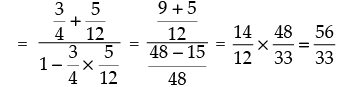
Hence, 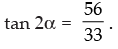
Q.5. If tan x = 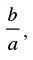 then find the value of
then find the value of 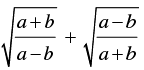
Ans.
Given that: tan x = 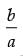
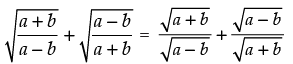
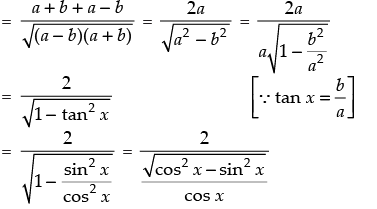
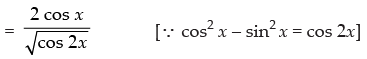
Hence, 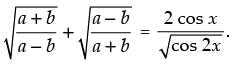
Q.6. Prove that cosθ cos 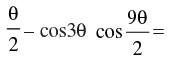 sin 7θ sin 8θ.
sin 7θ sin 8θ.
[Hint: Express L.H.S. = 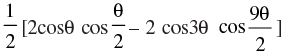
Ans.
L.H.S. 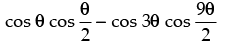
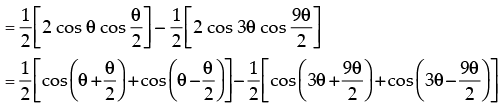
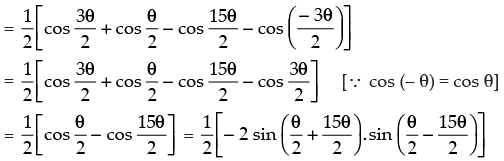
= – sin 8θ sin (– 7θ) = sin 7θ sin 8θ [∵ sin (-θ) = -sin θ]
L.H.S. = R.H.S. Hence proved.
Q.7. If a cos θ + b sin θ = m and a sin θ – b cos θ = n, then show that a2 + b2 = m2 + n2
Ans.
Given that: a cos θ + b sin θ
= m and a sin θ – b cos θ = n
R.H.S. = m2 + n2 = (a cos θ + b sin θ)2 + (a sin θ – b cos θ)2
= a2 cos2 θ + b2 sin2 θ + 2ab sin θ cos θ + a2 sin2 θ + b2 cos2 θ – 2ab sin θ cos θ
= a2 cos2 θ + b2 sin2 θ + a2 sin2 θ + b2 cos2 θ
= a2(cos2 θ + sin2 θ) + b2(sin2 θ + cos2 θ)
= a2.1 + b2.1 = a2 + b2 L.H.S.
L.H.S = R.H.S.
Hence proved.
Q.8. Find the value of tan 22°30 ′ .
[Hint: Let θ = 45°, use 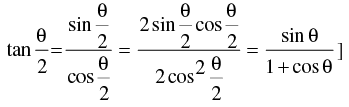
Ans.
Let 22°30’ 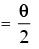 ∴ θ =45°
∴ θ =45°
tan 22°30’ 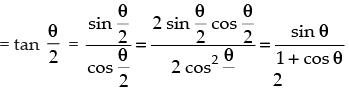
Put θ = 45°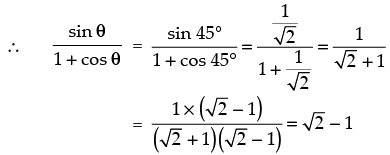
Hence, tan 22°30’ = √2 - 1
Q.9. Prove that sin 4A = 4sinA cos3A – 4 cosA sin3A.
Ans.
L.H.S. sin 4A = sin (A + 3A)
= sin A cos 3A + cos A sin 3A
= sin A(4 cos3 A – 3 cos A) + cos A(3 sin A – 4 sin3 A)
= 4 sin A cos3 A – 3 sin A cos A + 3 sin A cos A – 4 cos A sin3 A
= 4 sin A cos3 A – 4 cos A sin3 A. R.H.S.
L.H.S. = R.H.S.
Hence proved.
Q.10. If tanθ + sinθ = m and tanθ – sinθ = n, then prove that m2 – n2 = 4sinθ tanθ
[Hint: m + n = 2tanθ, m – n = 2 sinθ, then use m2 – n2 = (m + n) (m – n)]
Ans.
Given that: tan θ + sin θ = m and tan θ – sin θ = n
L.H.S. m2 – n2 = (m + n)(m – n)
= [(tan θ + sin θ) + (tan θ – sin θ)]. [(tan θ + sin θ) – (tan θ – sin θ)]
= (tan θ + sin θ + tan θ – sin θ).(tan θ + sin θ – tan θ + sin θ)
= 2 tan θ.2 sin θ= 4 sin θ tan θ. R.H.S.
L.H.S. = R.H.S. Hence proved.
Q.11. If tan (A + B) = p, tan (A – B) = q, then show that tan 2 A = 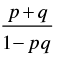
[Hint: Use 2A = (A + B) + (A – B)]
Ans.
Given that: tan (A + B) = p, tan (A – B) = q
tan 2A = tan (A + B + A – B) = tan [(A + B) + (A – B)]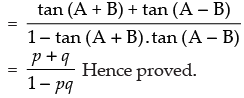
Q.12. If cosα + cosβ = 0 = sinα + sinβ, then prove that cos 2α + cos 2β = – 2cos (α + β).
[Hint: (cosα + cosβ)2 – (sinα + sinβ)2 = 0]
Ans.
Given that: cos α + cos β = 0 ................(i)
and sin α + sin α = 0 ...............(ii)
From (i) and (ii) we have
(cos α + cos β)2 – (sinα + sin β)2 = 0
⇒(cos2 α + cos2 β + 2 cos α cos β) – (sin2 α + sin2 β + 2 sin α sin β) = 0
⇒cos2 α + cos2 β + 2 cos α cos β – sin2 α – sin2 β – 2 sin α sin β = 0
⇒(cos2 α – sin2 α) + (cos2 β – sin2 β) + 2(cos α cos β – sin α sin β) = 0
⇒cos2 α + cos2 β + 2 cos (α + β) = 0
Hence, cos 2α + cos 2 β = – 2 cos (α + β).
Hence proved.
Q.13. If 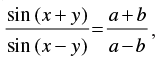 then show that
then show that
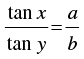
[Hint: Use Componendo and Dividendo].
Ans.
Given that: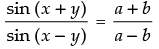
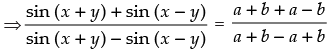
(Using componendo and dividendo theorem)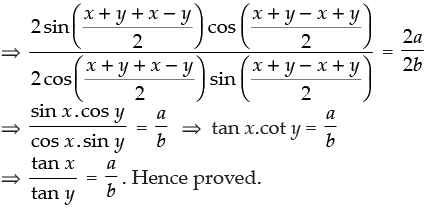
Q.14. If tanθ = 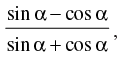 then show that sinα + cosα = √2 cosθ.
then show that sinα + cosα = √2 cosθ.
[Hint: Express tanθ = tan 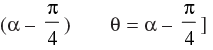
Ans.
Given that: 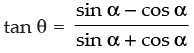
⇒ 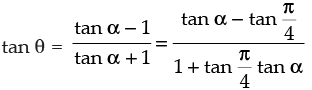
⇒ 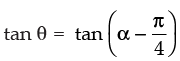
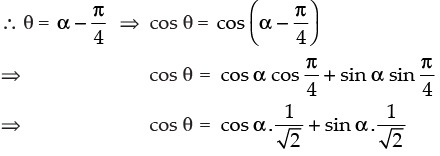
⇒ √2 cos θ = cos α + sin α
⇒ sin α + cos α = √2 cos θ.
Hence proved.
Q.15. If sinθ + cosθ = 1, then find the general value of θ.
Ans.
Given that: sin θ + cos θ = 1
Dividing both sides by 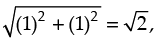 we get
we get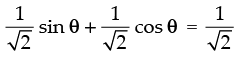 ...(1)
...(1)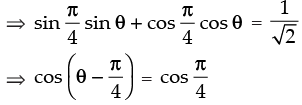
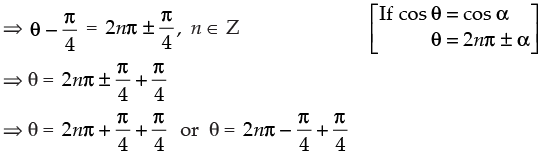
Hence, the general values of θ are 2nπ,n∈Z
Alternate method:
From eqn. (i) we get
Hence, the general value of 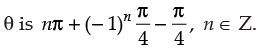
Q.16. Find the most general value of θ satisfying the equation tanθ = –1 and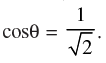
Ans.
Given that: tan θ = – 1 and cos θ = 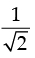
tan θ = – 1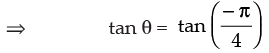
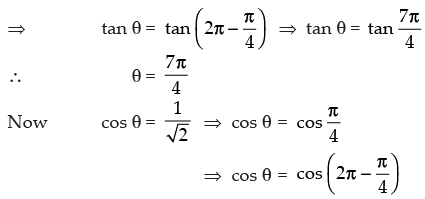
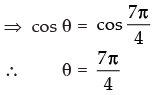
Hence, the general solution is 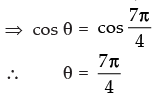
Q.17. If cotθ + tanθ = 2 cosecθ, then find the general value of θ.
Ans.
Given that: cot θ + tan θ = 2 cosec θ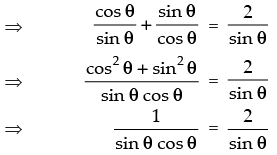
⇒ 2sin θ cos θ = sin θ
⇒ 2 sin θ cos θ – sin θ = 0
⇒ sin θ (2 cos θ – 1) = 0
⇒ sin θ = 0 or 2 cos θ – 1 = 0 or 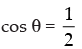
⇒ 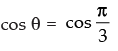
⇒ 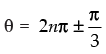
Hence, the general values of θ is 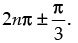
Q.18. If 2sin2θ = 3cosθ, where 0 ≤ θ ≤ 2π, then find the value of θ.
Ans.
Given that: 2 sin2 θ = 3 cos θ
⇒ 2(1 – cos2 θ) = 3 cos θ
⇒ 2 – 2 cos2 θ – 3 cos θ = 0
⇒ 2 cos2 θ + 3 cos θ – 2 = 0
⇒ 2 cos2 θ+ 4 cos θ – cos θ – 2 = 0
⇒2 cos θ (cos θ + 2) – 1(cos θ + 2) = 0
⇒ (cos θ + 2) (2 cos θ – 1) = 0
⇒ cos θ + 2 = 0 or 2 cos θ – 1 = 0
⇒ cos θ ≠ - 2 [- 1 ≤ cos θ ≤ 1]
∴ 2 cos θ – 1 = 0
⇒ 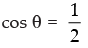
⇒ 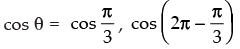
⇒ 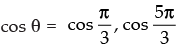
∴ 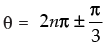
and 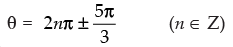
Hence, the value of θ are 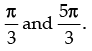
Q.19. If secx cos5x + 1 = 0, where 0 < x ≤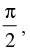 then find the value of x.
then find the value of x.
Ans.
Given that: sec x cos 5x + 1 = 0
⇒ 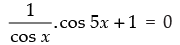
⇒ cos 5x + cos x = 0
⇒ 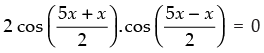
⇒ cos 3x . cos 2x = 0
⇒ cos 3x = 0 or cos 2x = 0
⇒ 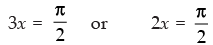
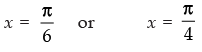
Hence, the values of x are 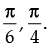
Long Answer Type
Q.20. If sin (θ + α) = a and sin (θ + β) = b, then prove that cos 2(α – β) – 4ab cos (α – β) = 1 – 2a2 – 2b2
[Hint: Express cos (α – β) = cos ((θ + α) – (θ + β))]
Ans.
Given that:
sin (θ + α) = a and sin (θ + β) = b .... (i)
cos (α - β) = cos [θ + α - θ – β) = cos [(θ + α) – (θ + β)]
∴ cos (α - β)= cos (θ + α) cos (θ + β) + sin (θ + α) sin (θ + β) 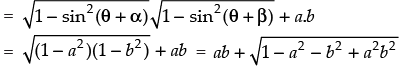
Now cos 2(α – β) – 4ab cos (α – β)
= 2 cos2 (α – β) – 1 – 4ab cos (α – β) [∴ cos 2θ = 2 cos2 θ – 1]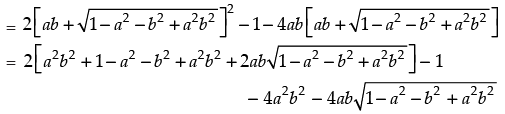
= 2a2 b2 + 2 - 2a2 - 2b2 + 2a2 b2 + 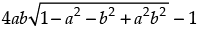
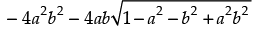
= 1 – 2a2 – 2b2
Hence, cos 2 (α - β) – 4ab cos (α - β) = 1 – 2a2 – 2b2.
Hence proved.
Q.21. If cos (θ + φ) = m cos (θ – φ), then prove that 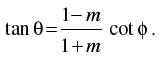
[Hint: Express 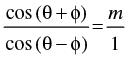 and apply Componendo and Dividendo]
and apply Componendo and Dividendo]
Ans.
Given that:
cos (θ + φ) = m cos (θ – φ)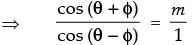
Using componendo and dividendo theorem, we get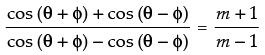
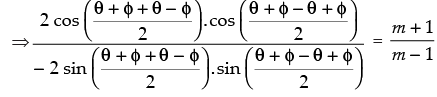
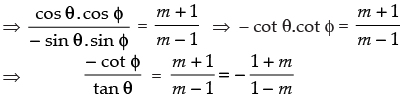
⇒ 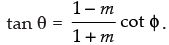
Hence proved.
Q.22. Find the value of the expression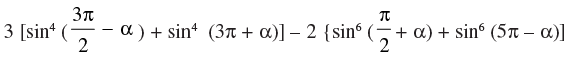
Ans.
Given that: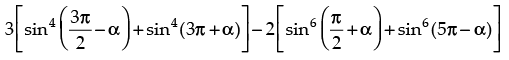
= 3[ cos4 α + sin4 (π + α)] – 2[cos6 α + sin6 (π - α)] = 3[cos4 α + sin4 α] – 2[cos6 α + sin6 α]
= 3[cos4 α + sin4 α + 2 sin2 α cos2 α - 2 sin2 α cos2 α] – 2[(cos2 α + sin2 α)3 – 3 cos2 α sin2 α (cos2 α + sin2 α)]
= 3[(cos2 α + sin2 α)2 – 2 sin2 α cos2 α] – 2[1 – 3 cos2 α sin2 α]
= 3[1 – 2 sin2 α cos2 α] – 2[1 – 3 cos2 α sin2 α]
= 3 – 6 sin2 α cos2 α - 2 + 6 cos2 α sin2 α
= 3 – 2 = 1
Hence, the value of the given expression is 1.
Q.23. If a cos 2θ + b sin 2θ = c has α and β as its roots, then prove that tanα + tan β = 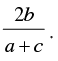
[Hint: Use the identities cos 2θ = 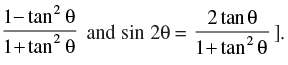
Ans.
Given that: a cos 2θ + b sin 2θ = c..... (i)
⇒ 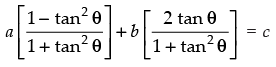
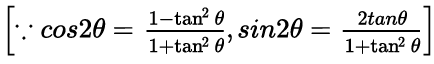
⇒ a – a tan2θ + 2b tanθ = c(1 + tan2 θ)
⇒ a – a tan2θ + 2b tan θ = c + c tan2 θ
⇒ a – a tan2θ + 2b tan θ – c tan2 θ – c = 0
⇒ - (a + c) tan2 θ + 2b tan θ + (a – c) = 0
⇒ (a + c) tan2 θ – 2b tan θ + (c – a) = 0..... (ii)
Since α and β are the roots of this equation
⇒ 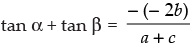
⇒ 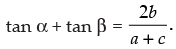 Hence proved.
Hence proved.
Q.24. If x = sec φ – tan φ and y = cosec φ + cot φ then show that xy + x – y + 1 = 0
[Hint: Find xy + 1 and then show that x – y = – (xy + 1)]
Ans.
Given that: x = sec φ – tan φ
and y = cosec φ + cot φ
xy + x – y + 1 = 0
L.H.S. xy + x – y + 1 = (sec φ – tan φ)
(cosec φ + cot φ) + (sec φ – tan φ) – (cosec φ + cot φ) + 1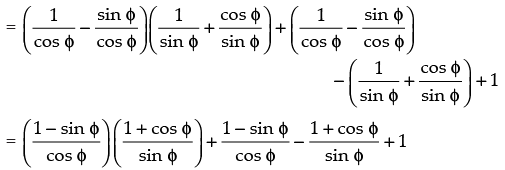
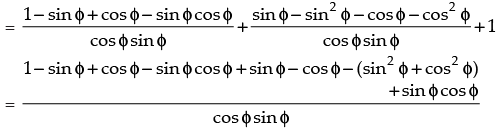
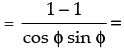 R.H.S.
R.H.S.
L.H.S. = R.H.S.
Hence proved.
Q.25. If θ lies in the first quadrant and cosθ = 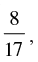 then find the value of
then find the value of
cos (30° + θ) + cos (45° – θ) + cos (120° – θ).
Ans.
Given that: 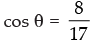
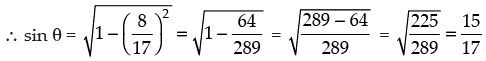
But θ lies in I quadrant.
∴ 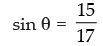
Now cos (30° + θ) + cos (45° – θ) + cos (120° – θ)
= cos 30° cos θ – sin 30° sin θ + cos 45° cos θ + sin 45° sin θ + cos 120° cos θ + sin 120° sin θ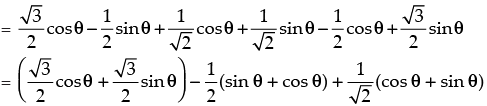
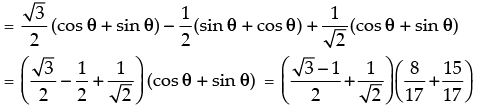
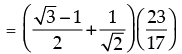
Hence, the required solution = 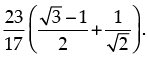
Q.26. Find the value of the expression 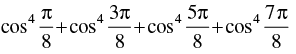
[Hint: Simplify the expression to 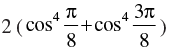
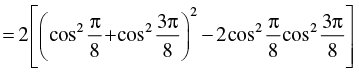
Ans.
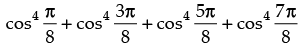
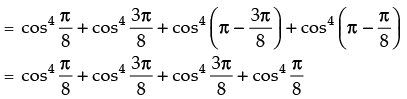
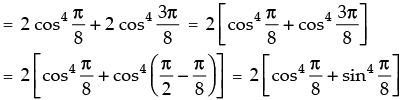
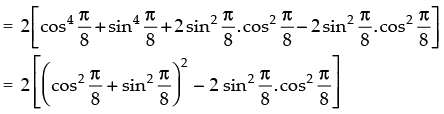
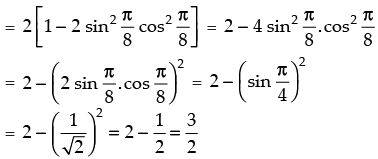
Hence, the required value of the expression = 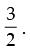
Q.27.Find the general solution of the equation
5cos2θ + 7sin2θ – 6 = 0
Ans.
5 cos2 θ + 7 sin2 θ – 6 = 0
⇒ 5 cos2 θ + 7(1 – cos2 θ) – 6 = 0
⇒ 5 cos2 θ + 7– 7 cos2 θ – 6 = 0
⇒ - 2 cos2 θ + 1 = 0
⇒ 2 cos2 θ = 1
⇒ 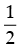
⇒ 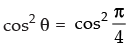
∴ 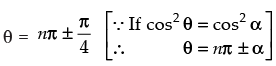
Hence, the general solution of 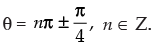
Q.28. Find the general solution of the equation
sinx – 3sin2x + sin3x = cosx – 3cos2x + cos3x
Ans.
Given that: sin x – 3 sin 2x + sin 3x = cos x – 3 cos 2x + cos 3x
⇒ (sin 3x + sin x) – 3 sin 2x = (cos 3x + cos x) – 3 cos 2x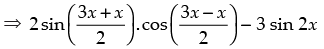
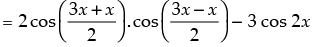
⇒ 2 sin 2x.cos x – 3 sin 2x = 2 cos 2x .cos x – 3 cos 2x
⇒ 2 sin 2x cos x – 2 cos 2x.cos x = 3 sin 2x – 3 cos 2x
⇒ 2 cos x(sin 2x – cos 2x) = 3(sin 2x – cos 2x)
⇒ 2 cos x (sin 2x – cos 2x) – 3(sin 2x – cos 2x) = 0
⇒ (sin 2x – cos 2x) (2 cos x – 3) = 0
⇒ sin 2x – cos 2x = 0 and 2 cos x – 3 ≠0 [∵ -1 ≤ cos x ≤ 1]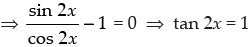
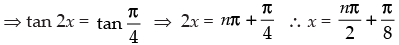
Hence, the general solution of the equation is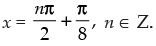
Q.29. Find the general solution of the equation ( √3 – 1) cosθ + ( √3 + 1) sinθ = 2
[Hint: Put √3 – 1= r sinα, √3 + 1 = r cosα which gives tanα = tan 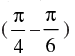
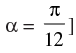
Ans.
Given that: ( √3 - 1) cos θ + ( √3 + 1) sin θ = 2
Put √3 - 1 = r sin α, √3 + 1 = r cos α
Squaring and adding, we get
r2 = √3 + 1 - 2 √3 + √3 + 1 + 2 √3
⇒ r2 = 8 ⇒r = ± 2 √2
Now the given equation can be written as
r sin α cos θ + r cos α sin θ = 2
⇒ r (sin α cos θ + cos α sin θ = 2
⇒ r (sin α cos θ + cos α sin θ) = 2
⇒2 √2 sin ( α + θ) = 2
⇒ sin (α + θ) = 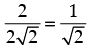
⇒ sin (α+ θ) = 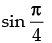
∴ 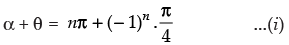
Now 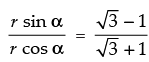
⇒ 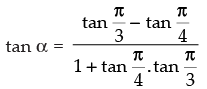
⇒ 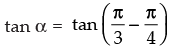
⇒ 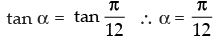
Putting the value of α in equation (i) we get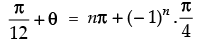
∴ 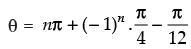
Hence, the general solution of the given equation is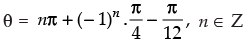
Objective Type Questions
Q.30. If sin θ + cosec θ = 2, then sin2 θ + cosec2 θ is equal to
(a) 1
(b) 4
(c) 2
(d) None of these
Ans. (c)
Solution.
Given that: sin θ + cosec θ = 2
Squaring both sides, we get
(sin θ + cosec θ)2 = (2)2
⇒ sin2 θ + cosec2 θ + 2 sin θ cosec θ = 4
⇒ sin2 θ + cosec2 θ + 2 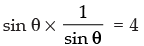
⇒ sin2 θ + cosec2 θ + 2 = 4
⇒ sin2 θ + cosec2 θ = 2
Hence, the correct option is (c).
Q.31. If f (x) = cos2 x + sec2 x, then
(a) f (x) < 1
(b) f (x) = 1
(c) 2 < f (x) < 1
(d) f(x) ≥ 2
[Hint: A.M ≥ G.M.]
Ans. (d)
Solution.
Given that: f(x) = cos2 x + sec2 x
We know that AM ≥ GM
⇒ 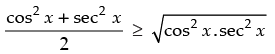
⇒ 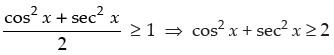
⇒ f(x) ≥ 2
Hence, the correct option is (d)
Q.32. If tan θ = 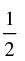 and tan φ =
and tan φ =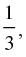 then the value of θ + φ is
then the value of θ + φ is
(a) π/6
(b) π
(c) 0
(d) π/4
Ans. (d)
Solution.
We know that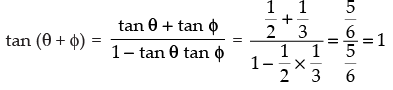
⇒ 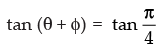
∴ 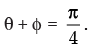
Hence the correct option is (d).
Q.33. Which of the following is not correct?
(a) 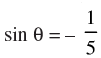
(b) cos θ = 1
(c) 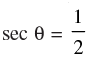
(d) tan θ = 20
Ans. (c)
Solution.
sin θ =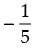 is correct. ∵1 ≤ sin θ ≤ 1
is correct. ∵1 ≤ sin θ ≤ 1
So (a) is correct.
cos θ = 1 is correct. ∵ cos 0° = 1
So (b) is correct.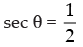
⇒ cos θ = 2 is not correct.
∵ - 1 ≤ cos θ ≤ 1
Hence, (c) is not correct.
Q.34. The value of tan 1° tan 2° tan 3° ... tan 89° is
(a) 0
(b) 1
(c) 1/2
(d) Not defined
Ans. (b)
Solution.
Given that: tan 1° tan 2° tan 3° .... tan 89°
= tan 1° tan 2° tan 3° .... tan 45°.tan (90 – 44°).tan (90 – 43°) ...tan (90 – 1°)
= tan 1° cot 1°.tan 2°.cot 2°.tan 3°.cot 3° ... tan 89°.cot 89°
= 1.1.1.1 ... 1.1 = 1
Hence, the correct option is (b).
Q.35. The value of 
(a) 1
(b) √3
(c) √3/2
(d) 2
Ans. (c)
Solution.
Given that: 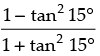
Let θ = 15° ∴ 2θ = 30°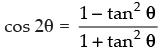
⇒ 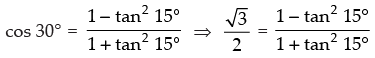
Hence, the correct option is (c).
Q.36. The value of cos 1° cos 2° cos 3° ... cos 179° is
(a) 1/√2
(b) 0
(c) 1
(d) –1
Ans. (b)
Solution.
Given expression is cos 1°.cos 2°.cos 3° ... cos 179°
⇒cos 1°.cos 2°.cos 3° ... cos 90°.cos 91° ... cos 179°
⇒ 0 [∵ cos 90° = 0]
Hence, the correct option is (b).
Q.37. If tan θ = 3 and θ lies in third quadrant, then the value of sin θ is
(a)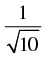
(b) 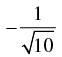
(c) 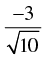
(d) 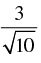
Ans. (c)
Solution.
tan θ = 3, θ lies in third quadrant, it is positive.
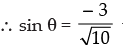 where θ lies in third quadrant
where θ lies in third quadrant
Hence the correct option is (c).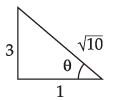
Q.38. The value of tan 75° – cot 75° is equal to
(a) 2√3
(b) 2 + √3
(c) 2 − √3
(d) 1
Ans. (a)
Solution.
The given expression is tan 75° – cot 75°
tan 75° – cot 75° = tan 75° – cot (90 – 15°)
= tan 75° – tan 15° = 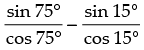
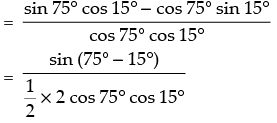
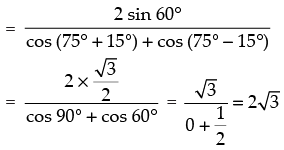
Hence, the correct option is (a).
Q.39. Which of the following is correct?
(a) sin1° > sin 1
(b) sin 1° < sin 1
(c) sin 1° = sin 1
(d) 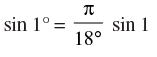
Ans. (b)
Solution.
We know that if θ increases then the value of sin θ also increases
So, sin 1° < sin 1 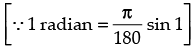
Hence the correct option is (b).
Q.40. If tan α = 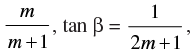 then α + β is equal to
then α + β is equal to
(a) 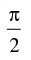
(b) 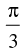
(c) 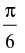
(d) 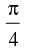
Ans. (d)
Solution.
Given that 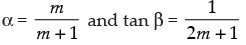
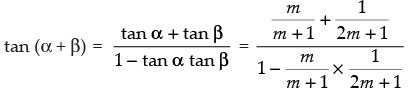
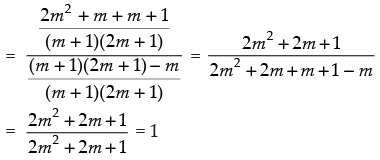
⇒ tan (α + β) 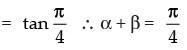
Hence, the correct option is (d).
Q.41. The minimum value of 3 cosx + 4 sinx + 8 is
(a) 5
(b) 9
(c) 7
(d) 3
Ans. (d)
Solution.
The given expression is 3 cos x + 4 sin x + 8
Let y = 3 cos x + 4 sin x + 8
⇒ y – 8 = 3 cos x + 4 sin x
Minimum value of y – 8 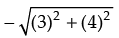
⇒ y – 8 = 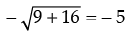
⇒ y = 8 – 5 = 3
So, the minimum value of the given expression is 3.
Hence, the correct option is (d).
Q.42. The value of tan 3A – tan 2A – tan A is equal to
(a) tan 3A tan 2A tan A
(b) – tan 3A tan 2A tan A
(c) tan A tan 2A – tan 2A tan 3A – tan 3A tan A
(d) None of these
Ans. (a)
Solution.
The given expression is tan 3A – tan 2A – tan A
tan 3A = tan (2A + A)
⇒ 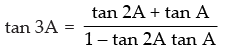
⇒ tan 3A(1 – tan 2A tan A) = tan 2A + tan A
⇒ tan 3A – tan 3A tan 2A tan A = tan 2A + tan A
⇒ tan 3A – tan 2A – tan A = tan 3A tan 2A tan A
Hence, the correct option is (a).
Q.43. The value of sin (45° + θ) – cos (45° – θ) is
(a) 2 cosθ
(b) 2 sinθ
(c) 1
(d) 0
Ans. (d)
Solution.
Given expression is (sin 45° + θ) – cos (45°- θ)
Sin (45° + θ) = sin 45° cos θ + cos 45° sin θ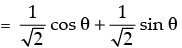
Cos (45° - θ) = cos 45° cos θ + sin 45° sin θ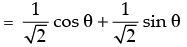
Sin (45°+ θ - cos (45°- θ)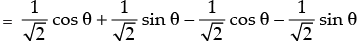
= 0.
Hence, the correct option is (d).
Q.44. The value of 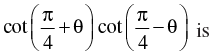
(a) 2 cosθ
(b) 2 sinθ
(c) 1
(d) 0
Ans. (c)
Solution.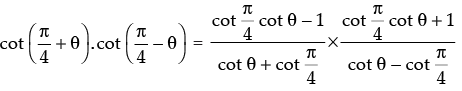
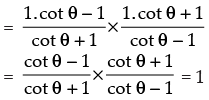
Hence, the correct option is (c).
Q.45. cos 2θ cos 2φ + sin2 (θ – φ) – sin2 (θ + φ) is equal to
(a) sin 2(θ + φ)
(b) cos 2(θ + φ)
(c) sin 2(θ – φ)
(d) cos 2(θ – φ)
[Hint: Use sin2 A – sin2 B = sin (A + B) sin (A – B)]
Ans. (b)
Solution.
Given that: cos 2θ.cos 2 φ + sin2 (θ - φ) – sin2 (θ + φ)
Cos 2θ cos 2φ + sin2 (θ - φ) – sin2 (θ + φ)
= cos 2θ cos 2φ + sin (θ - φ + θ + φ).sin (θ - φ - θ - φ)
[∵ sin2 A – sin2 B = sin (A + B).sin (A – B)]
= cos 2θ cos 2φ + sin 2θ.sin ( - 2φ)
= cos 2θ cos 2φ - sin 2θ sin 2φ [ ∵ sin(φ - θ) = - sin θ]
= cos 2(θ + φ)
Hence, the correct option is (b).
Q.46. The value of cos 12° + cos 84° + cos 156° + cos 132° is
(a) 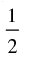
(b) 1
(c) 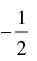
(d) 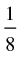
Ans. (c)
Solution.
The given expression is cos 12° + cos 84° + cos 156° + cos 132° (cos 132° + cos 12°) + (cos 156° + cos 84°)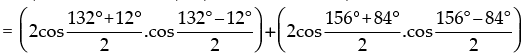
= 2 cos 72°.cos 60° + 2 cos 120°.cos 36°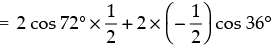
= cos 72° – cos 36°
= cos (90° – 18°) – cos 36° = sin 18° – cos 36°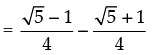
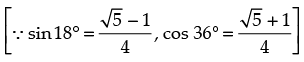
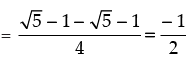
Hence, the correct option is (c).
Q.47. If tan A = 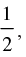 tan B =
tan B =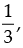 then tan (2A + B) is equal to
then tan (2A + B) is equal to
(a) 1
(b) 2
(c) 3
(d) 4
Ans. (c)
Solution.
Given that: tan A = 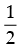 and tan B =
and tan B =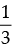
tan 2A = 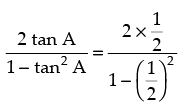
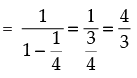
So, tan 2A = 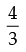 and tan B =
and tan B =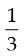
tan (2A + B) =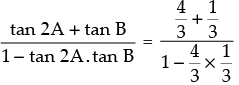
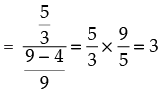
Hence, the correct option is (c).
Q.48. The value of 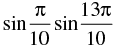 is
is
(a) 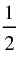
(b) 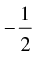
(c) 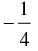
(d) 1
Ans. (c)
Solution.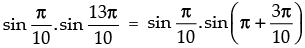
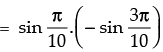
= – sin 18°.sin 54°
= – sin 18°.sin (90° – 36°) = – sin 18°.cos 36°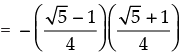
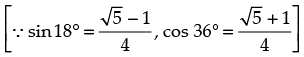
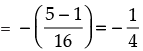
Hence, the correct option is (c).
Q.49. The value of sin 50° – sin 70° + sin 10° is equal to
(a) 1
(b) 0
(c) 1/2
(d) 2
Ans. (b)
Solution.
Given expression is sin 50° – sin 70° + sin 10°
(sin 50° – sin 70°) + sin 10°= 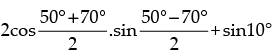
= 2 cos 60°.(– sin 10°) + sin 10°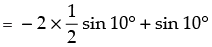
= – sin 10° + sin 10°
= 0
Hence, the correct option is (b).
Q.50. If sin θ + cos θ = 1, then the value of sin 2θ is equal to
(a) 1
(b) 1/2
(c) 0
(d) –1
Ans. (c)
Solution.
Given that:
sin θ + cos θ = 1
Squaring both sides, we get,
⇒ (sin θ + cos θ)2 = (1)2
⇒ sin2 θ + cos2 θ + 2 sin θ cos θ = 1
⇒ 1 + sin2 θ = 1
⇒ sin2 θ = 1 – 1 = 0
Hence, the correct option is (c).
Q.51. If α + β =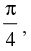 then the value of (1 + tan α) (1 + tan β) is
then the value of (1 + tan α) (1 + tan β) is
(a) 1
(b) 2
(c) – 2
(d) Not defined
Ans. (b)
Solution.
Given that: 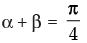
⇒ 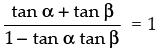
⇒ tan α + tan β = 1– tan α tan β
⇒ tan α + tan β + tan α tan β = 1
On adding 1 both sides, we get,
⇒ 1 + tan α + tan β + tan α tan β = 1 + 1
⇒ 1(1 + tan α) + tan β (1 + tan α) = 2
⇒ (1 + tan α )(1 + tan β) = 2
Hence, the correct option is (b)
Q.52. If sin θ = 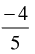 and θ lies in third quadrant then the value of
and θ lies in third quadrant then the value of
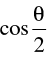 is
is
(a) 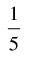
(b) 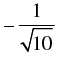
(c) 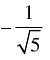
(d) 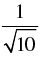
Ans. (c)
Solution.
Given that: 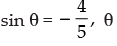 lies in third quadrant
lies in third quadrant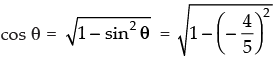
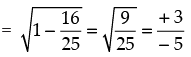
∴ 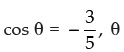 lies in third quadrant
lies in third quadrant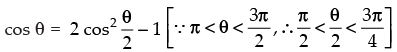
⇒ 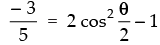
⇒ 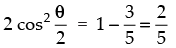
⇒ 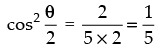
⇒ 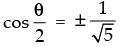
⇒ 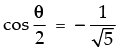
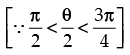
Hence, the correct option is (c).
Q.53. Number of solutions of the equation tan x + sec x = 2 cosx lying in the interval [0, 2π] is
(a) 0
(b) 1
(c) 2
(d) 3
Ans. (c)
Solution.
Given equation is tan x + sec x = 2 cos x
⇒ 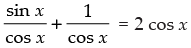
⇒ 1 + sin x = 2 cos2 x
⇒ 2 cos2 x – sin x – 1 = 0
⇒ 2(1 – sin2 x) – sin x – 1 = 0
⇒ 2 – 2 sin2 x – sin x – 1 = 0
⇒ – 2 sin2 x – sin x + 1 = 0
⇒ sin2 x + sin x – 1 = 0
Since, the equation is a quadratic equation in sin x.
So it will have 2 solutions.
Hence, the correct option is (c).
Q.54. The value of 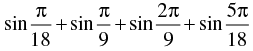 is given by
is given by
(a) 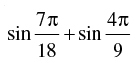
(b) 1
(c) 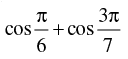
(d) 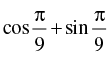
Ans. (a)
Solution.
The given expression is 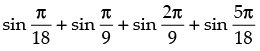
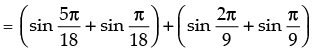
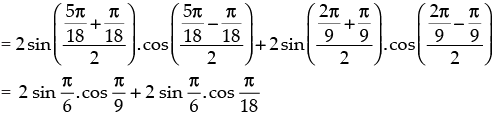
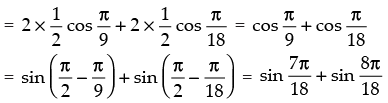
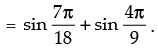
Hence, the correct option is (a).
Q.55. If A lies in the second quadrant and 3 tan A + 4 = 0, then the value of 2 cot A – 5 cos A + sin A is equal to
(a) 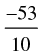
(b) 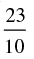
(c) 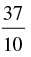
(d) 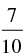
Ans. (b)
Solution.
Given that: 3 tan A + 4 = 0, A lies in second quadrant
∴ 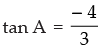
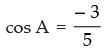
[A lies in second quadrant]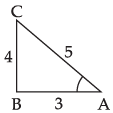
and 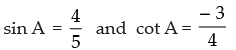
∴ 2 cot A – 5 cos A + sin A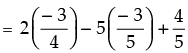
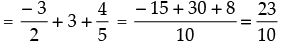
Hence, the correct option is (b).
Q.56. The value of cos2 48° – sin2 12° is
(a) 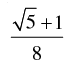
(b) 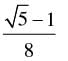
(c) 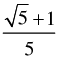
(d) 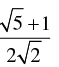
[Hint: Use cos2 A – sin2 B = cos (A + B) cos (A – B)]
Ans. (a)
Solution.
Given expression is cos2 48° – sin2 12°
cos2 48° – sin2 12° = cos (48° + 12°).cos (48° – 12°)
[∵ cos2 A – sin2 B = cos (A + B).cos (A – B)]
= cos 60°.cos 36°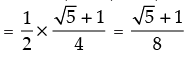
Hence, the correct option is (a).
Q.57. If tan α =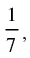 tan β =
tan β =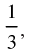 then cos 2α is equal to
then cos 2α is equal to
(a) sin 2β
(b) sin 4β
(c) sin 3β
(d) cos 2β
Ans. (b)
Solution.
Given that: 
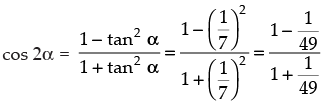
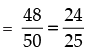
Now 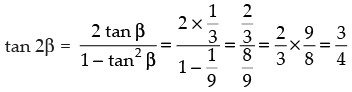
∴ 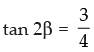
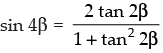
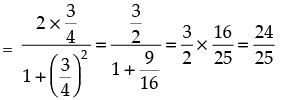
cos 2α = sin 4β =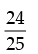
Hence, the correct option is (b).
Q.58. If tan θ = 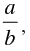 then b cos 2θ + a sin 2θ is equal to
then b cos 2θ + a sin 2θ is equal to
(a) a
(b) b
(c) a/b
(d) None
Ans. (b)
Solution.
Given that: 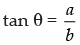
b cos 2θ + a sin 2θ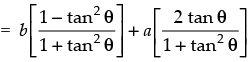
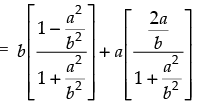
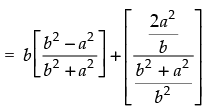
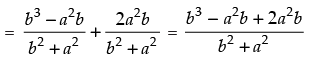
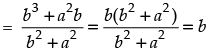
Hence, the correct option is (b).
Q.59. If for real values of x, cos θ =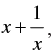 then
then
(a) θ is an acute angle
(b) θ is right angle
(c) θ is an obtuse angle
(d) No value of θ is possible
Ans. (d)
Solution.
Given that: 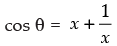
⇒ 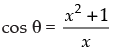
⇒ x2 + 1 = x cos θ
⇒ x2 – x cos θ + 1 = 0
For real value of x, b2 – 4ac ≥ 0
⇒ (- cos θ)2 – 4 × 1 × 1 ≥ 0
⇒ cos2 θ – 4 ≥ 0
⇒ cos2 θ ≥ 4
⇒ cos θ ≥ 2 [- 1 ≤ cos θ ≤ 1]
So, the value of θ is not possible.
Hence, the correct options (d).
Fill in the blanks
Q.60. The value of  is _______ .
is _______ .
Ans. 
Hence, the value of filler is 1.
Q.61. If k =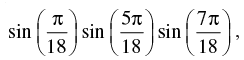 then the numerical value of k is _______.
then the numerical value of k is _______.
Ans.
Given that: k = 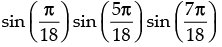
⇒ k = sin 10°. Sin 50°. Sin 70°
⇒ k = sin 10° sin (90° - 40°) sin (90° - 20°)
⇒ k = sin 10° cos 40° cos 20°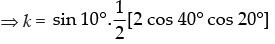

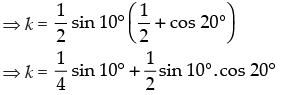
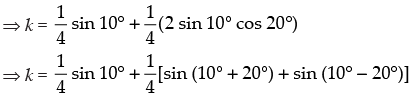
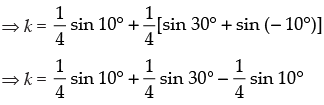
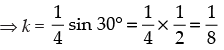
Hence, the value of the filler is 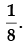
Q.62. If tan A =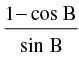 , then tan 2A = _______.
, then tan 2A = _______.
Ans.
Given that: tan A = 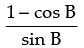
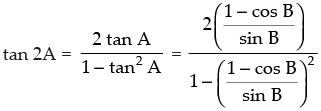
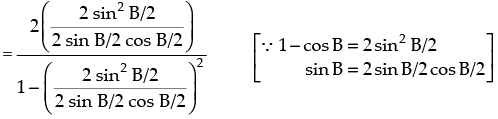
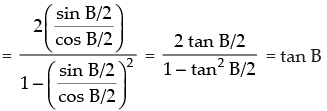
So, tan 2A = tan B
Hence, the value of the filler is tan B.
Q.63. If sin x + cos x = a, then
(i) sin6 x + cos6x = _______
(ii) | sin x – cos x | = _______.
Ans.
Given that: sin x + cos x = a
Squaring both sides, we get,
(sin x + cos x)2 = a2
⇒ sin2 x + cos2 x + 2 sin x cos x = a2
⇒ 1 + 2 sin x cos x = a2
⇒ sin x cos x = 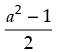 ...(i)
...(i)
(i) sin6 x + cos6 x = (sin2 x)3 + (cos2 x)3
= (sin2 x + cos2 x)3 – 3 sin2 x cos2 x(sin2 x + cos2 x)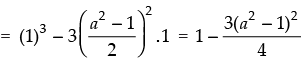
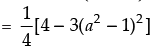
Hence, the value of the filler is 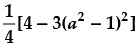
(ii) |sin x – cos x|2 = sin2 x + cos2 x – 2 sin x cos x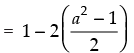
= 1 – (a2 – 1)
= 1 – a2 + 1
= 2 – a2
∴ |sin x – cos x| = 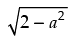
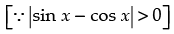
Hence, the value of the filler is 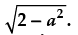
Q.64. In a triangle ABC with ∠C = 90° the equation whose roots are tan A and tan B is _______.
[Hint: A + B = 90° ⇒ tan A tan B = 1 and tan A + tan B = 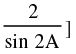
Ans.
Given a ΔABC with ∠C = 90°
x2 – (tan A + tan B)x + tan A.tan B = 0
A + B = 90° [∵ ∠C = 90°]
⇒ tan (A + B) = tan 90°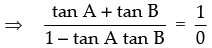
⇒ 1 – tan A tan B = 0
⇒ tan A tan B = 1……(i)
Now tan A + tan B = 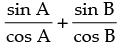
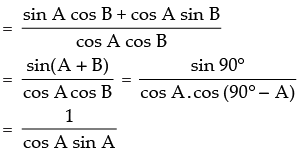
∴ tan A + tan B =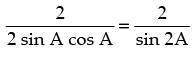 ……(ii)
……(ii)
From (i) and (ii) we get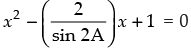
Hence, the value of the filler is 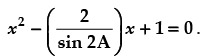
Q.65. 3 (sin x – cos x)4 + 6 (sin x + cos x)2 + 4 (sin6 x + cos6 x) = ______.
Ans.
Given expression is 3(sin x – cos x)4 + 6(sin x + cos x)2 + 4(sin6 x + cos6 x)
= 3[sin2 x + cos2 x – 2 sin x cos x]2 + 6(sin2 x + cos2 x + 2 sin x cos x) + 4 [(sin2 x)3 + (cos2 x)3]
= 3[1 – 2 sin x cos x]2 + 6(1 + 2 sin x cos x) + 4[(sin2 x + cos2 x)3 – 3 sin2 x cos2 x (sin2 x + cos2 x)]
= 3[1 + 4 sin2 x cos2 x – 4 sin x cos x] + 6(1 + 2 sin x cos x) + 4[1 – 3 sin2 x cos2 x]
= 3 + 12 sin2 x cos2 x – 12 sin x cos x + 6 + 12 sin x cos x + 4 – 12 sin2 x cos2 x
= 3 + 6 + 4 = 13
Hence, the value of the filler is 13.
Q.66. Given x > 0, the values of f (x) = – 3 cos 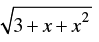 lie in the interval _______.
lie in the interval _______.
Ans.
Given that: f(x) =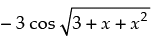
Put 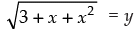
∴ f(x) = - 3 cos y
∵ - 1 ≤ cos y ≤ 1
3 ≥ - 3 cos y ≥ -3
⇒ - 3 ≤ - 3 cos y ≤ 3
∴ - 3 ≤ - 3 cos ≤ 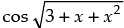 , x > 0
, x > 0
Hence, the value of the filler is [– 3, 3].
Q.67. The maximum distance of a point on the graph of the function y = √3 sin x + cos x from x-axis is _______.
Ans.
Given that y = √3 sin x + cos x ...(i)
∴ The maximum distance from a point on the graph of eqn. (i) from x-axis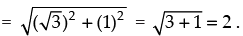
Hence, the value of the filler is 2.
state whether the statements is True or False? Also give justification.
Q.68. If tan A =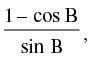 then tan 2A = tan B
then tan 2A = tan B
Ans.
Given that: tan A 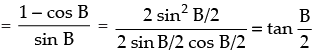
tan 2A = 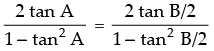
∴ tan 2A = tan B
Hence, the statement is ‘True’.
Q.69. The equality sin A + sin 2A + sin 3A = 3 holds for some real value of A.
Ans.
Given that: sin A + sin 2A + sin 3A = 3
Since the maximum value of sin A is 1 but for sin 2A
and sin 3A it is not equal to 1. So it is not possible.
Hence, the given statement is ‘False’.
Q.70. Sin 10° is greater than cos 10°.
Ans.
If sin 10° > cos 10°
⇒ sin 10° > cos (90° – 80°)
⇒sin 10° > sin 80°
which is not possible.
Hence, the statement is ‘False’.
Q.71. 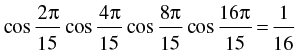
Ans.
L.H.S. 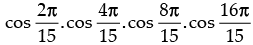
= cos 24°.cos 48°.cos 96°.cos 192°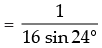 [(2 sin 24 cos 24 )(2 cos 48 )(2 cos 96 )(2 cos 192 )]
[(2 sin 24 cos 24 )(2 cos 48 )(2 cos 96 )(2 cos 192 )]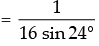 [sin 48 .2 cos 48 (2 cos 96 )(2 cos 192 )]
[sin 48 .2 cos 48 (2 cos 96 )(2 cos 192 )]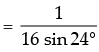 [2 sin 48 cos 48 (2 cos 96 )(2 cos 192 )]
[2 sin 48 cos 48 (2 cos 96 )(2 cos 192 )]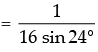 [sin 96 (2 cos 96 )(2 cos 192 )]
[sin 96 (2 cos 96 )(2 cos 192 )]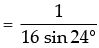 [2 sin 96 . cos 96 (2 cos 192 )]
[2 sin 96 . cos 96 (2 cos 192 )]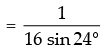 [sin 192 .(2 cos 192 )]
[sin 192 .(2 cos 192 )]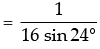 2 sin 192 cos 192
2 sin 192 cos 192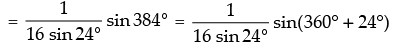
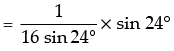 [∵ sin (360° + θ) = sin θ]
[∵ sin (360° + θ) = sin θ]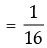 R.H.S.
R.H.S.
Hence, the given statement is ‘True’.
Q.72. One value of θ which satisfies the equation sin4 θ – 2sin2 θ – 1 lies between 0 and 2π.
Ans. Given equation is
sin4 θ – 2 sin2 θ – 1 = 0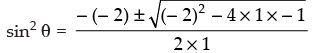
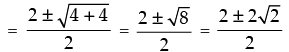
= 1 ± √2
∴ sin2 θ = (1 + √2 ) or (1 - √2 )
⇒ - 1 ≤ sin q ≤ 1
⇒ sin2 θ ≤ 1 but sin2 θ = (1 + √2 ) or (1 - √2 )
Which is not possible.
Hence, the given statement is ‘False’.
Q.73. If cosec x = 1 + cot x then x = 2nπ, 2nπ +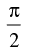
Ans.
Given that: cosec x = 1 + cot x
⇒ 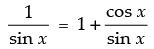
⇒ 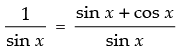
⇒ sin x + cos x = 1
⇒ 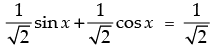
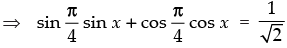
⇒ 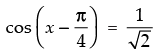
⇒ 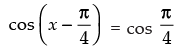
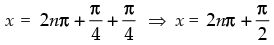
or 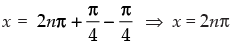
Hence, the given statement is ‘True’.
Q.74. If tan θ + tan 2θ + √3 tan θ tan 2θ = √3 , then 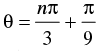
Ans.
Given that:tan θ + tan 2θ + √3 tan θ tan 2θ = √3
⇒ tan θ + tan 2θ = √3 - √3 tan θ tan 2θ
⇒ tan θ + tan 2θ = √3 (1 - tan θ tan 2θ)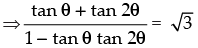
⇒ tan (θ + 2θ) = √3
⇒ 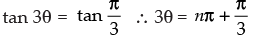
So 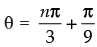
Hence, the given statement is ‘True’.
Q.75. If tan (π cosθ) = cot (π sinθ), then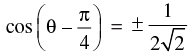
Ans.
Given that: tan (π cos θ) = cot (π sin θ)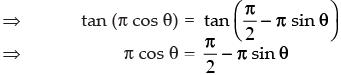
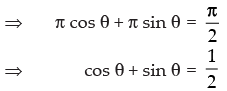
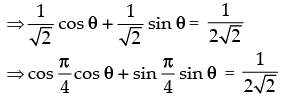
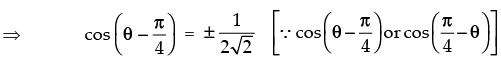
Hence, the given statement is ‘True’.
Q.76. In the following match each item given under the column C1 to its correct answer given under the column C2 :
| (a) sin (x + y) sin (x – y) | (i) cos2 x – sin2 y |
| (b) cos (x + y) cos (x – y) | 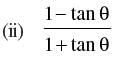 |
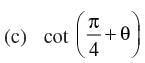 | 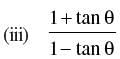 |
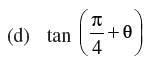 | (iv) sin2 x – sin2 y |
Ans.
(a) sin (x + y) sin (x – y) = sin2 x – sin2 y
∴ (a)↔(iv)
(b) cos (x + y) cos (x – y) = cos2 x – cos2 y
∴ (b) ↔ (i)
(c) 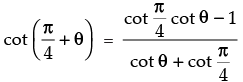
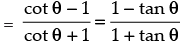
∴ (c) ↔ (ii)
(d) 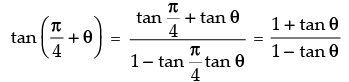
∴ (d) ↔ (iii)
Hence,
(a) ↔ (iv)
(b) ↔ (i)
(c) ↔ (ii)
(d) ↔ (iii).
|
172 videos|503 docs|154 tests
|
FAQs on NCERT Exemplar: Trigonometric Functions - Mathematics (Maths) for JEE Main & Advanced
| 1. What are trigonometric functions and why are they important in mathematics? |  |
| 2. How can I find the values of trigonometric functions for common angles? |  |
| 3. What is the significance of the unit circle in trigonometry? |  |
| 4. How do the graphs of trigonometric functions look, and what are their key characteristics? |  |
| 5. What are some practical applications of trigonometric functions in real life? |  |






















