NCERT Exemplar: Work, Energy & Power | Physics Class 11 - NEET PDF Download
MULTIPLE CHOICE QUESTIONS I
Q. 1. An electron and a proton are moving under the influence of mutual forces. In calculating the change in the kinetic energy of the system during motion, one ignores the magnetic force of one on another. This is because,
(a) The two magnetic forces are equal and opposite, so they produce no net effect.
(b) The magnetic forces do no work on each particle.
(c) The magnetic forces do equal and opposite (but non-zero) work on each particle.
(d) The magnetic forces are necessarily negligible.
Ans. (b)
Solution:
Key concept: To calculate the change in kinetic energy of the system during motion we have to apply work-energy, theorem. According to this theorem, Net work done = Final kinetic energy – Initial kinetic energy of the object The above statement shows the connection between work and kinetic energy as: “The work done by the net force acting on an object is equal to the change in the kinetic energy of that object”.
Net work done (IF) on a particle equals change in kinetic energy of the particle.
ΣW = K2-K1
According to the problem as the electron and proton are moving under the influence of mutual forces, the magnetic forces will be perpendicular to their motion, hence, it acts as a centripetal force for the particle. In this way the particle performs the uniform circular motion, this implies speed will remain constant. So, there is no change in kinetic energy of the particle. Hence no work is done by these forces.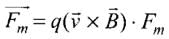
(magnetic force) will be perpendicular to both B and v, where B is the external magnetic field and v is the velocity of particle. That is why one ignores the magnetic force of one particle on another.
Q. 2. A proton is kept at rest. A positively charged particle is released from rest at a distance d in its field. Consider two experiments; one in which the charged particle is also a proton and in another, a positron. In the same time t, the work done on the two moving charged particles is
(a) Same as the same force law is involved in the two experiments.
(b) Less for the case of a positron, as the positron moves away more rapidly and the force on it weakens.
(c) More for the case of a positron, as the positron moves away a larger distance.
(d) Same as the work done by charged particle on the stationary proton.
Ans. (c)
Solution:
Force between two protons is equal to the force between proton and a
positron because their charges are same. As the mass of positron is much lesser than proton, (1/1840 times) it moves away through much larger distance compared to proton.
Change in their momentum will be same. So, velocity of lighter particle will be greater than that of a heavier particle. So, positron is moved through a larger distance.
As work done = force x distance. As forces are same in case of proton and positron but distance moved by positron is larger, hence, work done will be more.
Q. 3. A man squatting on the ground gets straight up and stand. The force of reaction of ground on the man during the process is
(a) constant and equal to mg in magnitude.
(b) constant and greater than mg in magnitude.
(c) variable but always greater than mg.
(d) at first greater than mg, and later becomes equal to mg.
Ans. In the process of squatting on the ground he gets straight up and stand. Then he is tilted somewhat, the man exerts a variable force on the ground to balance his weight, hence he also has to balance frictional force besides his weight in this case.
N = Normal reaction force = friction + mg => N > mg
Once the man gets straight up that variable force = 0 => Normal reaction force = mg
Q. 4. A bicyclist comes to a skidding stop in 10 m. During this process, the force on the bicycle due to the road is 200N and is directly opposed to the motion. The work done by the cycle on the road is
(a) + 2000J
(b) – 200J
(c) zero
(d) – 20,000J
Ans. (c)
Solution:
As the friction is present in fhis problem, so mechanical energy is not conserved. So energy will be lost due to dissipation by friction.^Here, work is done by the frictional force on the cycle and is equal to __ 200 x 10 = -2000 J
As the road does not move at all, therefore, work done by the cycle on the road is zero.
Important point: We should be aware that here the energy of bicyclist is lost during the motion, but it is lost due to friction in the form of heat.
Q. 5. A body is falling freely under the action of gravity alone in vacuum. Which of the following quantities remain constant during the fall?
(a) Kinetic energy.
(b) Potential energy.
(c) Total mechanical energy.
(d) Total linear momentum.
Ans. (c)
Solution:
During free fall, K.E. increases, momentum increases and P.E. decreases
Total mechanical energy=K.E.+P.E.
As P.E. decreases and K.E. increases ∴ M.E. remains constant.
Q. 6. During inelastic collision between two bodies, which of the following quantities always remain conserved?
(a) Total kinetic energy.
(b) Total mechanical energy.
(c) Total linear momentum.
(d) Speed of each body.
Ans. (c)
Solution :
If in a collision kinetic energy after collision is not equal to kinetic energy before collision, the collision is said to inelastic.
Coefficient of restitution 0 < e < 1
When we are considering the two bodies as system the total external force on the system
will be zero.
Hence, total linear momentum of the system remain conserved.
Here kinetic energy appears in other forms, i.e. energy may be lost in the form of heat and sound etc. In some cases (KE)final < (KE)initial
such as when initial KE is converted into intertial energy of the product (as heat, elastic or excitation)
while in other cases (KE)final > (KE)initial
such as when internal energy stored in the colliding particles is released.
Examples’.
(1) Collision between two billiard balls.
(2) Collision between two automobiles on a road.
In fact all majority of collisions belong to this category.
Q. 7. Two inclined frictionless tracks, one gradual and the other steep meet at A from where two stones are allowed to slide down from rest, one on each track as shown in Fig.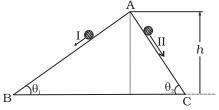 Which of the following statement is correct?
Which of the following statement is correct?
(a) Both the stones reach the bottom at the same time but not with the same speed.
(b) Both the stones reach the bottom with the same speed and stone I reaches the bottom earlier than stone II.
(c) Both the stones reach the bottom with the same speed and stone II reaches the bottom earlier than stone I.
(d) Both the stones reach the bottom at different times and with different speeds.
Ans. (c)
Solution:
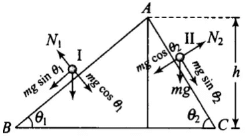
As shown in diagram AB and AC are two smooth planes inclined to the angle θ1 and θ2 respectively. As friction is absent here, hence, mechanical energy will be conserved. As both the tracks having common height h,
From conservation of mechanical energy,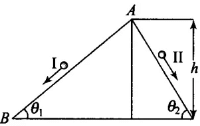
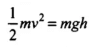 (for both tracks I and II)
(for both tracks I and II)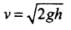
Hence, speed is same for both stones. For stone I, a1 = acceleration along inclined plane = g sinθ1
Similarly, for stone II,
a2 = g sinθ2 as θ2 > θ1, hence, a2 > a1.
And both length for track II is also less, hence stone II reaches earlier than stone I.
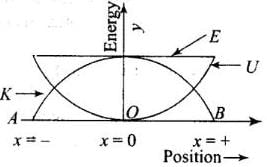
Q. 8. The potential energy function for a particle executing linear SHM is given by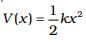 where k is the force constant of the oscillator (Fig). For
where k is the force constant of the oscillator (Fig). For
k = 0.5N/m, the graph of V(x) versus x is shown in the figure. A particle of total energy E turns back when it reaches x = 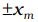 . If V and K indicate the P.E. and K.E., respectively of the particle at x = +xm, then which of the following is correct?
. If V and K indicate the P.E. and K.E., respectively of the particle at x = +xm, then which of the following is correct?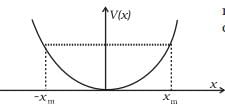 (a) V = O, K = E
(a) V = O, K = E
(b) V = E, K = O
(c) V < E, K = O
(d) V = O, K < E
Ans. (b) Solution:
Solution:
Key concept: Energy Graph for a Spring: If the mass attached with spring performs simple harmonic motion about its mean position then its potential energy at any position (x) can be given by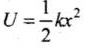 ................(i)
................(i)
So for the extreme position,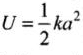 [As x = ±a for extreme]
[As x = ±a for extreme]
This is maximum potential energy or he total energy of mass.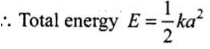 ................ (ii)
................ (ii)
[Because velocity of mass = 0 at extreme position]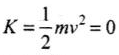
 Now kinetic energy at any position
Now kinetic energy at any position
K = E - U = 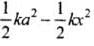
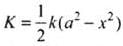
From the above formula, we can check that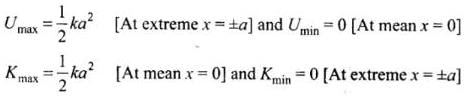
E =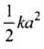 = constant (at all positions)
= constant (at all positions)
It means kinetic energy changes parabolically w.r.t. position but total energy remain always constant irrespective to the position of mass.
Total energy is E = PE + KE, which remains constant.
According to the question, when particle is at x = xm, i.e. at extreme position
x = xm =» KE = 0
Hence, total energy will be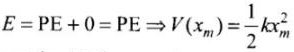
Hence option (b) is correct.
V = E , K = 0
Q. 9. Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V as shown in FigIf the collision is elastic, which of the following (Fig) is a possible result after collision?
(a)
(b)
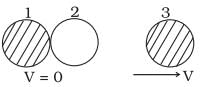
(c)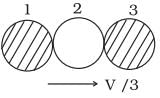
(d)
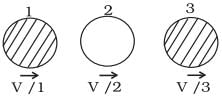 Ans. (b)
Ans. (b)
Solution:
Key concept: In a collision if the motion of colliding particles before and after the collision is along the same line, the collision is said to be head on or one dimensional. When two bodies of equal masses collides elastically, their velocities are interchanged. Kinetic energy and linear momentum remains conserved Total kinetic energy of the system before collision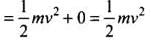
In (a), kinetic energy of the system after collision."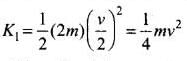
Hence this option is incorrect.
In (b), kinetic energy of the system after collision,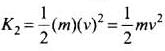
Hence this option will be correct.
In (c), kinetic energy of the system after collision.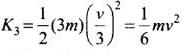
Hence this option is incorrect.
In (d), kinetic energy of the system after collision,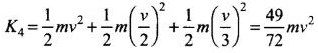
We see that kinetic energy is conserved only in (b).
Q.10. A body of mass 0.5 kg travels in a straight line with velocity v = ax3/2 where a = 5 m-1/2 s_1. The work done by the net force during its displacement from x = 0 to; x = 2m is
(a) 5 J
(b) 50 J
(c) 10 J
(d) 100 J
Ans. Key concept: When a variable force acts on a particle while it moves from point A to B, say along the path shown in the figure, work done by the force on the particle is given by on the particle is given by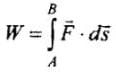 ............. (i)
............. (i)Here,
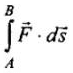 is to be integrated along the path the particle follows.
is to be integrated along the path the particle follows.
The vector integral is equivalent to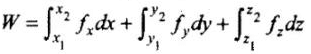
According to the problem, velocity = ax3/2, mass = 0.5 kg, a = 5 m-1/2 s-1, we have to find work done (W) by net force.
We know that
Acceleration,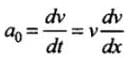
= 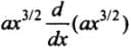
= 
Net Force = mao = m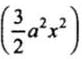
And work done due to variable force,
Work done = 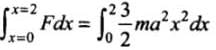
= 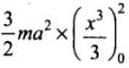
= 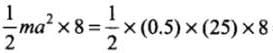
= 50 J
Q. 11. A body is moving unidirectionally under the influence of a source of constant power supplying energy. Which of the diagrams shown in figure correctly shown the displacement-time curve for its motion?
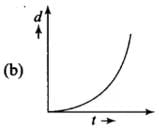
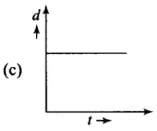
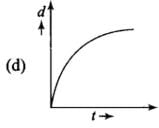
Ans. (b)
Solution:
For constant power Displacement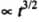
Because
P =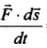 =
=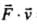 = constant
= constant
(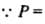 constant according to the problem)
constant according to the problem)
Now, will by dimensional analysis
[F)[v] = constant
=>[MLT-2][LT-1] = constant
= L2T-3 = constant (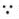 mass is constant)
mass is constant)
= L T3/2
T3/2
=> Displacement ( d )  t3/2
t3/2
Q. 12. Which of the diagrams shown in Fig. 6.6 most closely shows the variation in kinetic energy of the earth as it moves once around the sun in its elliptical orbit?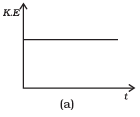
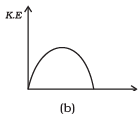
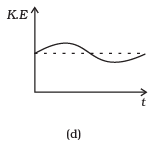
Ans. (d)
Solution:
As the earth moves once around the sun in its elliptical orbit, when the earth is closest to the sun, speed of the earth is maximum, hence KE is maximum. When the earth is farthest from the sun speed is minimum, hence KE is minimum but never zero and negative.
This variation of KE vs t is correctly represented by option (d).
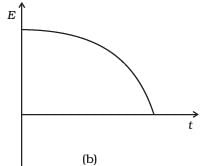
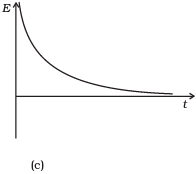
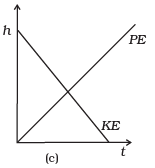
Q. 13. Which of the diagrams shown in Fig represents variation of total mechanical energy of a pendulum oscillating in air as function of time?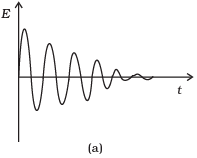
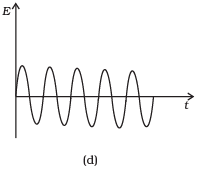 Ans. (c)
Ans. (c)
Solution:
When a pendulum oscillates in air, its total mechanical energy decreases continuously in overcoming resistance due to air. Therefore, total mechanical energy of the pendulum decreases exponentially with time.
The variation of E vs t is correctly represented by curve (c) in which the relation between energy and time is shown.
Q. 14. A mass of 5 kg is moving along a circular path of radius 1 m. If the mass moves with 300 revolutions per minute, its kinetic energy would be
(a) 250π2
(b) 100π2
(c) 5π2
(d) 0
Ans. According to the problem, Radius =1 m, mass = m = 5 kg
Frequency of revolution, f = 300 rev/min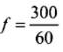
Angular velocity will be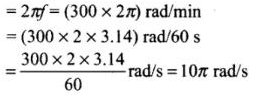
And relation between linear velocity and angular velocity is, v = ωR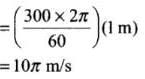
And kinetic energy = 1/2 mv2
=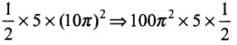
= 250 π2J
Q. 15. A raindrop falling from a height h above ground, attains a near terminal velocity when it has fallen through a height (3/4)h. Which of the diagrams shown in Fig correctly shows the change in kinetic and potential energy of the drop during its fall up to the ground?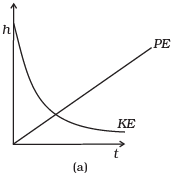
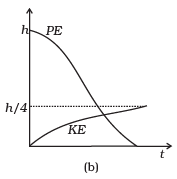
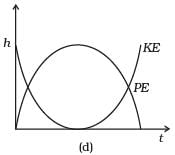 Ans. (b)
Ans. (b)
Solution:
At height h from ground raindrop have maximum potential energy. And kinetic velocity will be zero (at the instant when it dropped its velocity will be zero), then as the rain drop falls its PE starts decreasing and kinetic energy start increasing.
The total mechanical energy will remain conserved if we neglect the air resistance. If there is some air resistance, there is some force called upthrust (in fluids) which opposes its motion. It depends upon velocity of object as the velocity increases, upthrust also increases. Hence during fall of raindrop first its velocity increases and then become constant after some time.
This constant velocity is called terminal velocity, hence KE also become constant. PE decreases continuously as the drop is falling continuously.
The variation in PE and KE is best represented by (b).
Q. 16. In a shotput event an athlete throws the shotput of mass 10 kg with an initial speed of 1m s-1 at 45° from a height 1.5 m above ground. Assuming air resistance to be negligible and acceleration due to gravity to be 10 m s-2 , the kinetic energy of the shotput when it just reaches the ground will be
(a) 2.5 J
(b) 5.0 J
(c) 52.5 J
(d) 155.0 J
Ans. (d)
Solution: If air resistance is negligible, total mechanical energy of the system will remain constant. And let us take ground as a reference where potential energy will be zero.
According to the problem, h = 1.5 m, v = 1 m/s, m = 10 kg, g = 10 ms– 2
Initial energy of the shotput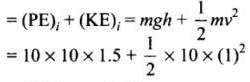
= 150 + 5 = 155 J
From conservation of mechanical energy,
(PE)i + (K E )i = (PE)f + ( K E )f
=> 155j = 0 + (KE)f
So, final kinetic energy of the shotput is 155 J.
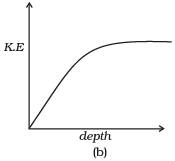
Q. 17. Which of the diagrams in Fig correctly shows the change in kinetic energy of an iron sphere falling freely in a lake having sufficient depth to impart it a terminal velocity?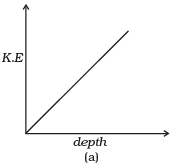
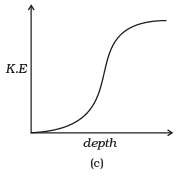
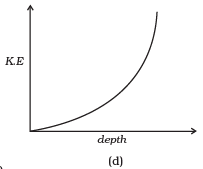 Ans. (b)
Ans. (b)
Solution: When an iron sphere is falling freely in the lake, it will accelerate by the force due to gravity then its velocity increases continuously and resistance due to water cause a force called viscous force or upthrust (in fluids) which opposes its motion. It depends upon velocity of object as the velocity increases upthrust increases. Hence during fall of sphere first its velocity increases and then become constant after some depth.
This constant velocity is called terminal velocity, hence KE become constant beyond this depth, which is best represented by (b).
Q. 18. A cricket ball of mass 150 g moving with a speed of 126 km/h hits at the middle of the bat, held firmly at its position by the batsman.
The ball moves straight back to the bowler after hitting the bat.
Assuming that collision between ball and bat is completely elastic and the two remain in contact for 0.001s, the force that the batsman had to apply to hold the bat firmly at its place would be
(a) 10.5 N
(b) 21 N
(c) 1.05 ×104 N
(d) 2.1 × 104 N
Ans. We know that force F
And the magnitude o f force will be, F = 2mv/t
According to the problem, m = 150 g =
Δt = time of contact = 0.001 s
u = 126 km/h =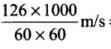
= 35 m/s
v = -126 km/h = -35 m/s
Change in momentum o f the ball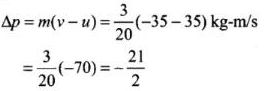
We know that force F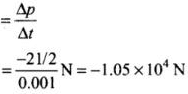
Here, - ve sign shows that force will be opposite to the direction o f movement o f the ball before hitting. So the force that the batsman had to apply to hold the bat firmly at its place would be F = 1.05 x 104 N k
MULTIPLE CHOICE QUESTIONS - II
Q. 19. A man, of mass m, standing at the bottom of the staircase, of height L climbs it and stands at its top.
(a) Work done by all forces on man is equal to the rise in potential energy mgL.
(b) Work done by all forces on man is zero.
(c ) Work done by the gravitational force on man is mgL.
(d) The reaction force from a step does not do work because the point of application of the force does not move while the force exists.
Ans. (b,d)
Solution:
When a man of mass m climbs up the staircase of height L, work done by the gravitational force on the man = -mgL
Work done by internal muscular forces = -Work done against gravitational force = mgL
Work done by all the forces = mgL – mgL = 0
As the point of application of the contact forces does not move, hence work done by reaction forces will also be zero.
And work done by friction will also be zero as there a no dissipation or rubbing is involved.
Q. 20 A bullet of mass m fired at 30° to the horizontal leaves the barrel of the gun with a velocity v. The bullet hits a soft target at a height h above the ground while it is moving downward and emerges out with half the kinetic energy it had before hitting the target.
Which of the following statements are correct in respect of bullet after it emerges out of the target?
(a) The velocity of the bullet will be reduced to half its initial value.
(b) The velocity of the bullet will be more than half of its earlier velocity.
(c ) The bullet will continue to move along the same parabolic path.
(d) The bullet will move in a different parabolic path.
(e) The bullet will fall vertically downward after hitting the target.
(f) The internal energy of the particles of the target will increase.
Ans. (b, d, f)
Solution: The given situation is shown in the diagram. Let speed after emerging from the target is v”, v’ is speed of the bullet just before hitting the target, v is the initial speed of bullet.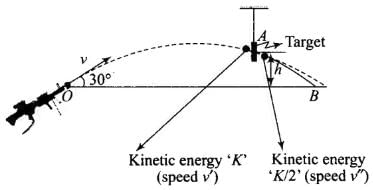 (a) The velocity of the bullet after it emerges out of the target will be reduced to half its initial value.
(a) The velocity of the bullet after it emerges out of the target will be reduced to half its initial value.
Compare the kinetic energies before and after hitting the target.Just before hitting the target the mechanical energy will be conserved. After hitting its energy will be loose. So by conservation of mechanical energy between “O” and “A” (A is the point where the target is placed),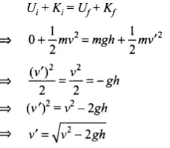 ............(i)
............(i)
Then,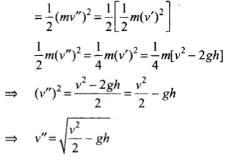 ...............(ii)
...............(ii)
From eq (i) and (ii),
Substituting in equation (i),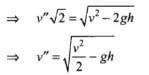
So as we increase the value of h, the value of v'' decreases.
So (a) is incorrect
(b) 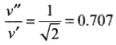
Hence, after emerging from the target velocity of the bullet (v”) is more than half of its earlier velocity v’ (velocity before emerging into the target). So option (b) is correct.
(c) Since velocity of the bullet is changed after hitting the target, so it follows a different parabolic path.
(d) As the velocity of the bullet changes to v’which is less than v’ hence path followed will change and the bullet reaches at point B instead of A’, as shown in the figure.
(e) After emerging from the target, bullet follows a parabollic path, the bullet will not fall vertically downward, so it is an incorrect option.
(f) As the bullet is passing through the target, the loss in energy of the • bullet is transferred to particles of the target. Therefore, their internal energy increases.
Q. 21. Two blocks M1 and M2 having equal mass are free to move on a horizontal frictionless surface. M2 is attached to a massless spring as shown in Fig. Initially M2 is at rest and M1 is moving toward M2 with speed v and collides head-on with M2.
(a) While spring is fully compressed all the KE of M1 is stored as PE of spring.
(b) While spring is fully compressed the system momentum is not conserved, though final momentum is equal to initial momentum.
(c) If spring is massless, the final state of the M1 is state of rest.
(d) If the surface on which blocks are moving has friction, then collision cannot be elastic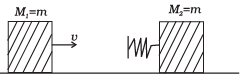 Ans.(c, d)
Ans.(c, d)
Solution:
If there is not specified we always consider the collision elastic.
When two bodies of equal masses collides elastically, their velocities are interchanged in these types of collision.
Kinetic energy and linear momentum remain conserved.
According to the above diagram when m1 comes in contact with the spring, m1 is retarded by the spring force and m2 is accelerated by the spring force.
(a) The spring will continue *to compress until the two blocks acquire common velocity. So some of kinetic energy of block Mx store into P.E and some part of it stores into K.E of block M2. So option (a) is incorrect.
(b) As surfaces are frictionalless momentum of the system will be conserved. So option (b) is also incorrect.
(c) The two bodies of equal mass exchange their velocities in a head on elastic collision between them. So, if spring is massless, the final state of the M1 is state of rest.
(d) Since there is a loss of K.E when the blocks collides on the rough surface. Hence, the collision is inelastic.
VERY SHORT ANSWER TYPE QUESTIONS
Q. 22. A rough inclined plane is placed on a cart moving with a constant velocity u on horizontal ground. A block of mass M rests on the incline. Is any work done by force of friction between the block and incline? Is there then a dissipation of energy?
Ans. Let us consider the diagram according to the situation. Just imagine the situation that wedge is moving with velocity u. As the block Mis at rest with respect to the inclined plane. There is no pseudo force acting on the block because the wedge is moving with constant velocity. So,
f = frictional force = Mg sinθ (upward as shown in the figure)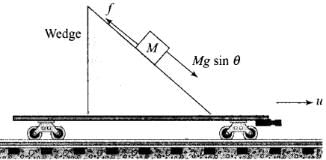 As the block rests on the incline, the force of friction acting between the block and the incline opposes the tendency of sliding of the block. Since, block is not in motion with respect to incline, therefore, work done by the force of friction between the block and the inclined plane is zero. Also due to this reason there is no dissipation of energy.
As the block rests on the incline, the force of friction acting between the block and the incline opposes the tendency of sliding of the block. Since, block is not in motion with respect to incline, therefore, work done by the force of friction between the block and the inclined plane is zero. Also due to this reason there is no dissipation of energy.
Q. 23. Why is electrical power required at all when the elevator is descending? Why should there be a limit on the number of passengers in this case?
Ans. When the elevator is descending, then electric motor (mainly induction motor are used) provides some force to overcome the weight of elevator to prevent it from falling freely under gravity, then electric power is required to run electric motor which is holding the elevator via cable to prevent it from falling freely. This cable is able to sustain some limiting value of tension developed in it. Due to this reason, it is needed to limit the number of passengers in the elevator.
Q. 24. A body is being raised to a height h from the surface of earth.
What is the sign of work done by
(a) Applied force
(b) Gravitational force?
Ans. (a) External force is applied on the body to lift it in upward direction against its weight, therefore, angle between the applied force and displacement is = 0°
Work done by the applied force
W= F. S =Fs cos = Fs cos 0° = Fs ( cos 0° = 1)
i.e., the sign of work done by applied force is positive.
(b) As shown in figure the gravitational force acts in downward direction and displacement in upward direction, therefore, angle between them is = 180°.
Work done by the gravitational force
W = Fs cos 180° = -Fs (cos 180° = -1)

Q. 25. Calculate the work done by a car against gravity in moving along a straight horizontal road. The mass of the car is 400 kg and the distance moved is 2m.
Ans. Weight of the car (mg) vertically downward and car is moving along horizontal road, so displacement of the car is in the along horizontal, i.e. angle between them is 90°.
Work done by weight of the car
W = Fs cos 90° = 0, (cos 90° = 0)
Hence, the work done by car against gravity will also be zero.
Q. 26. A body falls towards earth in air. Will its total mechanical energy be conserved during the fall? Justify.
Ans. If we neglect the air resistance then the total mechanical energy of the body is conserved but if there is some air resistance then a small part of its energy is utilized against resistive force of air, which is non-conservative force. So, total mechanical energy of the body falling freely under gravity in this case is not conserved. In this condition, gain in KE < loss in PE.
Let E be the total mechanical energy.
Initial mechanical energy of the body
Intermediate mechanical energy of the body will be
So,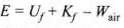
Hence, total mechanical energy of the body will not be conserved.
Q. 27. A body is moved along a closed loop. Is the work done in moving the body necessarily zero? If not, state the condition under which work done over a closed path is always zero.
Ans. Key concept: If the work done by a force on a body depends upon the initial and final positions only of that body, then the force is conservative e.g., gravitational, electrostatic, magnetic forces.
If the work done by a force on a body which has moved in closed path and has come back to its initial position is zero, the force is conservative.
Work done in moving along a closed loop is not always zero. Work done in moving a closed path is zero when forces acting on the body are conservative but for non-conservative forces like friction force, viscous force etc. work done in a closed path is not zero.
Q. 28. In an elastic collision of two billiard balls, which of the following quantities remain conserved during the short time of collision of the balls (i.e., when they are in contact)?
(a) Kinetic energy
(b) Total linear momentum
Give reason for your answer in each case.
Ans. During collision no external force is acting on the balls, therefore total linear momentum of the system of two balls is always conserved.
During collision when the balls are in contact, there may be deformation, hence some kinetic energy of system will be transformed to potential energy of system and consequently kinetic energy will not be conserved.
Important point: Though kinetic energy of system will not be conserved but total energy of the system will be conserved.
Q. 29. Calculate the power of a crane, in watts, which lifts a mass of 100 kg to a height of 10 m in 20 s.
Ans. According to the problem, mass = m= 100 kg height = h- 10 m, time interval, t = 20 s Power is the rate of doing work with respect to time.
Q. 30. The average work done by a human heart while it beats once is 0.5 J. Calculate the power used by heart if it beats 72 times in a minute.
Ans. According to the problem, average work done by a human heart per beat = 0.5 J
Total work done during 72 beats in 1 minute
= 72 x 0.5 J =36 J
Power = Work done = 36 J / 60s = 0.6 w
Q. 31. Give example of a situation in which an applied force does not result in a change in kinetic energy.
Ans. Assume a ball tied to a string and is moving in a vertical circle. Work done by tension force will be zero and hence tension force will not cause any change in KE of ball. Because at any instant of time the displacement is tangential and the force is central in nature, i.e., tension in the string and the small displacement at any instant are perpendicular to each other.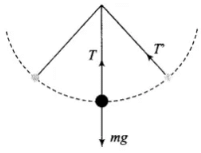
Q. 32. Two bodies of unequal mass are moving in the same direction with equal kinetic energy. The two bodies are brought to rest by applying retarding force of same magnitude. How would the distance moved by them before coming to rest compare?
Ans. According to work-energy theorem,
Change in KE is equal to work done by all the forces acting on the body. Let us assume that only one force (retarding force) is acting on the body, therefore,
KE of the body = Work done by retarding force KE of the body = Retarding force x Displacement
As KE of the bodies and retarding forces applied on them are same, therefore, both bodies will travel equal distances before coming to rest.
Q. 33. A bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in Fig. What will be the trajectory of the particle if the string is cut at
(a) Point B?
(b) Point C?
(c) Point X? Ans. When the bob is whirled into circular path the required centripetal force is provided by string (towards the centre of circular path) due to tension and it balances by centrifugal force provided by tangential velocity of particle.
Ans. When the bob is whirled into circular path the required centripetal force is provided by string (towards the centre of circular path) due to tension and it balances by centrifugal force provided by tangential velocity of particle.
Hence, when string is cut off, the centripetal force become zero and bob moves with tangential velocity under gravity.
(a) When string is cut off at B, it’s tangential velocity will be vertically downward, so bob will move along vertical path under gravity.
(b) When string is cut off at C. bob has horizontal velocity, so bob will move in half parabolic path as shown in figure.
(c) When string is cut off at X then the velocity of bob is makes some angle 9 with horizontal so it moves parabolic path reaches at higher height then again parabolic.
SHORT ANSWER TYPE QUESTIONS
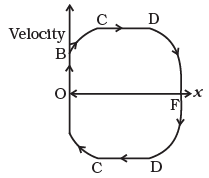
Q. 34. A graph of potential energy V (x) verses x is shown in Fig. A particle of energy E0 is executing motion in it. Draw graph of velocity and kinetic energy versus x for one complete cycle AFA.
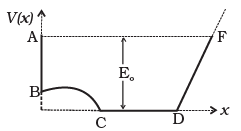 Ans. (i) KE versus x graph: By the law of conservation of energy:
Ans. (i) KE versus x graph: By the law of conservation of energy:
Total Mechanical energy.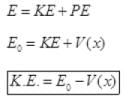
At point A
PE is maximum,
E = KE + PE
E0 = KE + V(x)
K.E. = E0 - V(x)
At point A
PE is maximum,
PE = E0 KE = E0- E0 = 0
KE = E0- E0 = 0
At B, x = 0 PE = VB(let)
KE = E0-V0
At C , x = xi PE = 0 KE = Eo - V(x) = E0 - 0 = E0
KE = Eo - V(x) = E0 - 0 = E0
At D, x = x2 KE = Eo
At E, x= x3 PE = E0 KE = 0
KE = 0
Figure shows graph KE versus x
| X | KE | Point |
| 0 | 0 | A |
| 0 | E1 | B |
| x1 | E0 | C |
| x2 | E0 | D |
| x3 | 0 | F |
(ii) Velocity (v) versus (x):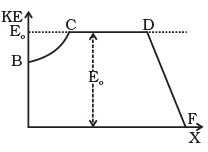 KE = -mv
KE = -mv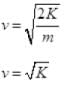
| Point | v | X |
| A | 0 | 0 |
| B | 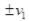 | 0 |
| C | 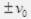 | x1 |
| D | 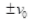 | x2 |
| E | 0 | x3 |
 At point A and F
At point A and F
KE = 0
and xA = O, xD - x3
At C and D, xc = x1, xD = x2
KE = E0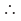 vmax =
vmax =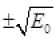 = v0
= v0 At B, x = 0 KE = E1
At B, x = 0 KE = E1 vB =
vB = 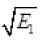 = ± v
= ± v
(v - x) graph is shown in given figure here."
Q. 35. A ball of mass m, moving with a speed 2v0, collides inelastically (e > 0) with an identical ball at rest. Show that
(a) For head-on collision, both the balls move forward.
(b) For a general collision, the angle between the two velocities of scattered balls is less than 90°.
Ans.
(a) For head on collision:
Conservation of momentum ⇒ 2mv0 = mv1 + mv2
Or 2v0 = v1 + v2
and
⇒ v2 = v1+ 2v0e ∴ 2v1 = 2v0 – 2ev0 ∴ v1 = v0(1 – e)Since e <1 ⇒ v 1 has the same sign as v 0, therefore the ball moves on after collission.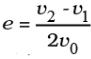
=> v2 = v1+ 2v0e
∴ 2v1 = 2v0 – 2ev0
∴ v1 = v0(1 – e)
Since e <1 ⇒ v1 has the same sign as v0, therefore the ball moves on after collission.
(b) Conservation of momentum ⇒ p = p1+ p2
But KE is lost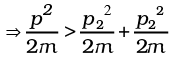
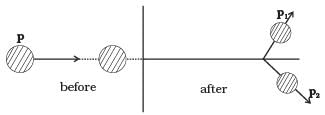

∴ p2 > p12 + p22
Thus p, p1 and p2 are related as shown in the figure.
θ is acute (less than 90°) (p2 = p12 + p22 would give θ = 90°)
Q. 36. Consider a one-dimensional motion of a particle with total energy E. There are four regions A, B, C and D in which the relation between potential energy V, kinetic energy (K) and total energy E is as given below:
Region A : V > E
Region B : V < E
Region C : K > E
Region D : V > K
State with reason in each case whether a particle can be found in the given region or not.
Ans. Region A : No, as KE will become negative.
Region B : Yes, total energy can be greater than PE for non zero K.E.
Region C : Yes, KE can be greater than total energy if its PE is negative.
Region D : Yes, as PE can be greater than KE.
Q. 37. The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in Fig.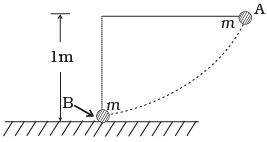 If the length of the pendulum is 1m, calculate
If the length of the pendulum is 1m, calculate
(a) the height to which bob A will rise after collision.
(b) the speed with which bob B starts moving.
Neglect the size of the bobs and assume the collision to be elastic.
Ans. Let m be the mass of the bob and h be the initial height of the bob.
Potential energy of a particle raised to the height h is = mgh
And kinetic energy of the particle with velocity v is given as =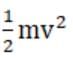
Just before collision, bob A reaches ground and its potential energy gets converted to kinetic energy,
∴ conserving energy we get,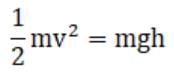
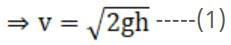
(a) Using the result that when two bodies of same mass collide, their velocities are mutually interchanged,
Bob A must come to rest and bob B must gain the velocity in equation (1).
a) ∴ from above we conclude the bob A will not rise to any height since its velocity will become zero after collision.
b) ∵ the velocities are interchanged,
∴ velocity of bob B = 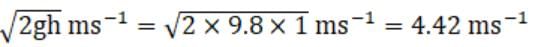
Q. 38. A raindrop of mass 1.00 g falling from a height of 1 km hits the ground with a speed of 50 m s–1. Calculate
(a) the loss of P.E. of the drop.
(b) the gain in K.E. of the drop.
(c) Is the gain in K.E. equal to loss of P.E.? If not why.
Take g = 10 ms-2
Ans. (a) Loss of PE = mgh = 1 ×10-3 ×10 ×10-3 =10J
(b) Gain in KE =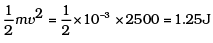
(c) No, because a part of PE is used up in doing work against the viscous drag of air.
Q. 39. Two pendulums with identical bobs and lengths are suspended from a common support such that in rest position the two bobs are in contact (Fig). One of the bobs is released after being displaced by 10o so that it collides elastically head-on with the other bob.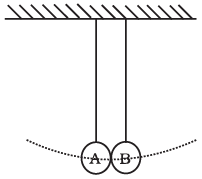 (a) Describe the motion of two bobs.
(a) Describe the motion of two bobs.
(b) Draw a graph showing variation in energy of either pendulum with time, for 0 ≤ t≤2T , where T is the period of each pendulum.
Ans. (b)
Solution: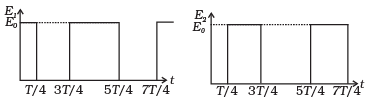
Q. 40. Suppose the average mass of raindrops is 3.0 × 10-5kg and their average terminal velocity 9 m s-1. Calculate the energy transferred by rain to each square metre of the surface at a place which receives 100 cm of rain in a year.
Ans. m = 3.0 × 10-5 kg ρ = 10-3 kg/m2 v = 9m/s
A = 1m2
h = 100 cm ⇒ n = 1m3
M = ρv = 10–3 kg,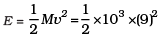
= 4.05 × 104 J
Q. 41. An engine is attached to a wagon through a shock absorber of length 1.5m. The system with a total mass of 50,000 kg is moving with a speed of 36 km h-1 when the brakes are applied to bring it to rest. In the process of the system being brought to rest, the spring of the shock absorber gets compressed by 1.0 m. If 90% of energy of the wagon is lost due to friction, calculate the spring constant.
Ans.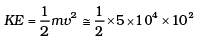
= 2.5 × 105 J.
10% of this is stored in the spring.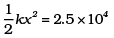
x = 1 m
k = 5 × 104 N/m.
Q. 42. An adult weighing 600N raises the centre of gravity of his body by 0.25 m while taking each step of 1 m length in jogging. If he jogs for 6 km, calculate the energy utilised by him in jogging assuming that there is no energy loss due to friction of ground and air.
Assuming that the body of the adult is capable of converting 10% of energy intake in the form of food, calculate the energy equivalents of food that would be required to compensate energy utilised for jogging.
Ans. In 6 km there are 6000 steps.
∴ E = 6000 (mg)h
= 6000 × 600 × 0.25
= 9 × 105J.
This is 10 % of intake.
∴ Intake energy = 10 E = 9 ×106J.
Q. 43. On complete combustion a litre of petrol gives off heat equivalent to 3×107 J. In a test drive a car weighing 1200 kg. including the mass of driver, runs 15 km per litre while moving with a uniform speed on a straight track. Assuming that friction offered by the road surface and air to be uniform, calculate the force of friction acting on the car during the test drive, if the efficiency of the car engine were 0.5.
Ans. With 0.5 efficiency, 1 litre generates 1.5 × 107 J, which is used for 15 km drive.
∴ F d = 1.5 ×107 J. with d = 15000 m
∴ F = 1000 N : force of friction.
LONG ANSWER TYPE QUESTIONS
Q. 44. A block of mass 1 kg is pushed up a surface inclined to horizontal at an angle of 30° by a force of 10 N parallel to the inclined surface (Fig).The coefficient of friction between block and the incline is 0.1. If the block is pushed up by 10 m along the incline, calculate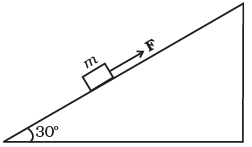 (a) work done against gravity
(a) work done against gravity
(b) work done against force of friction
(c) increase in potential energy
(d) increase in kinetic energy
(e) work done by applied force.
Ans. (a) Wg = mg sinθ d = 1 × 10 × 0.5 ×10 = 50 J.
(b) Wf = µ mg cosθ d = 0.1 ×10 × 0.866 × 10 = 8.66 J.
(c) ∆U = mgh = 1 × 10 × 5 = 50 J
(d) a = {F - (mgsinθ + µmgcosθ)}
= [10 - 5.87 ]
= 4.13 m/s2
v = u + at or v2 = u2 + 2ad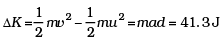
(e) W = F d = 100 J
Q. 45. A curved surface is shown in Fig. The portion BCD is free of friction. There are three spherical balls of identical radii and masses. Balls are released from rest one by one from A which is at a slightly greater height than C.
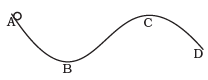 With the surface AB, ball 1 has large enough friction to cause rolling down without slipping; ball 2 has a small friction and ball 3 has a negligible friction.
With the surface AB, ball 1 has large enough friction to cause rolling down without slipping; ball 2 has a small friction and ball 3 has a negligible friction.
(a) For which balls is total mechanical energy conserved?
(b) Which ball (s) can reach D?
(c) For balls which do not reach D, which of the balls can reach back A?
Ans. (a) Energy is conserved for balls 1 and 3.
(b) Ball 1 acquires rotational energy, ball 2 loses energy by friction. They cannot cross at C. Ball 3 can cross over.
(c) Ball 1, 2 turn back before reaching C. Because of loss of energy, ball 2 cannot reach back to A. Ball 1 has a rotational motion in “wrong” sense when it reaches B. It cannot roll back to A, because of kinetic friction.
Q. 46. A rocket accelerates straight up by ejecting gas downwards. In a small time interval ∆t, it ejects a gas of mass ∆m at a relative speed u. Calculate KE of the entire system at t + ∆t and t and show that the device that ejects gas does work = (1/2) ∆mu2 in this time interval (neglect gravity).
Ans.
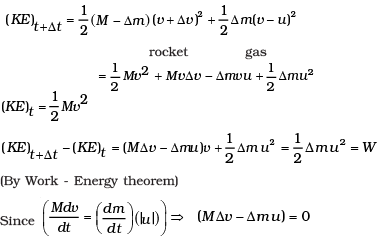
Q. 47. Two identical steel cubes (masses 50 g , side 1cm) collide head-on face to face with a speed of 10cm/s each. Find the maximum compression of each. Young’s modulus for steel = Y = 2 × 1011 N/m 2.
Ans. Hooke’s law : 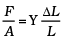
where A is the surface area and L is length of the side of the cube. If k is spring or compression constant, then F = k ∆ L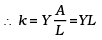
Initial KE =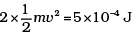
Final PE =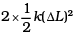
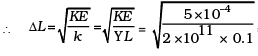
= 1.58 × 10–7m
Q. 48. A baloon filled with helium rises against gravity increasing its potential energy. The speed of the baloon also increases as it rises. How do you reconcile this with the law of conservation of mechanical energy? You can neglect viscous drag of air and assume that density of air is constant.
Ans. Let m , V, ρHe denote respectively the mass, volume and density of helium baloon and ρair be density of air Volume V of baloon displaces volume V of air.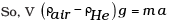 .................. (i)
.................. (i)
Integrating with respect to t,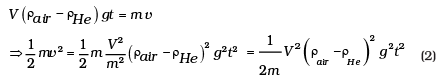
If the baloon rises to a height h , from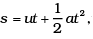
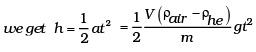 ............. (3)
............. (3)
From Eqs. (3) and (2),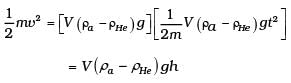
Rearranging the terms,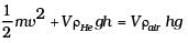
KEbaloon + PEbaloon = change in PE of air.
So, as the balloon goes up, an equal volume of air comes down, increase in PE and KE of the balloon is at the cost of PE of air [which comes down].
|
96 videos|367 docs|98 tests
|
FAQs on NCERT Exemplar: Work, Energy & Power - Physics Class 11 - NEET
| 1. What is work in the context of physics? |  |
| 2. How is work related to energy? |  |
| 3. What is the formula for calculating work? |  |
| 4. Can work be negative? |  |
| 5. What is power and how is it related to work? |  |
















