NCERT Exemplars - Electric Charges and Fields | Physics for Airmen Group X - Airforce X Y / Indian Navy SSR PDF Download
MULTIPLE CHOICE QUESTIONS - I
Q.1. In Fig.1.1, two positive charges q2 and q3 fixed along the y axis, exert a net electric force in the + x direction on a charge q1 fixed along the x axis. If a positive charge Q is added at (x, 0), the force on q1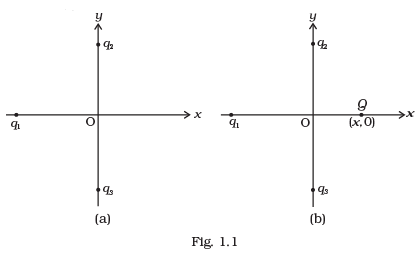 (a) Shall increase along the positive x-axis.
(a) Shall increase along the positive x-axis.
(b) Shall decrease along the positive x-axis.
(c) Shall point along the negative x-axis.
(d) Shall increase but the direction changes because of the intersection of Q with q2 and q3.
Ans. (a)
Solution. (i) As the resultant force on qj. due to q2 and q3 is along positive x direction. [Given]
(i) As the resultant force on qj. due to q2 and q3 is along positive x direction. [Given]
(ii) The vector sum of forces F12 and F13 is R, along positive x direction. So, F12 and F13 are attractive forces and |F12| = |F13| also.
(iii) So q1 is negative charges (as q2, q3 are positive charges.)
(iv) A Charges Q (x, O) is positive, so the force due to Q will be along positive x direction.
(v) As the direction of forces R (due to F12 and F21 and due to Q) are along positive x-axis, so the net force on q1 shall increase along positive x-axis.
Q.2. A point positive charge is brought near an isolated conducting sphere (Fig. 1.2). The electric field is best given by
(i)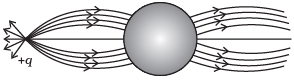
(ii) 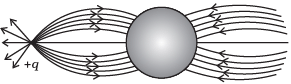
(iii) 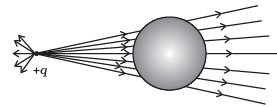
(iv) 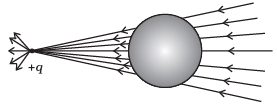
(a) Fig (i)
(b) Fig (ii)
(c) Fig (iii)
(d) Fig (iv)
Ans. (a)
Solution.
- Electric field lines come out of positive charge and go into the negative charge.
- Tangent to the field line at any point gives the direction of the field at that point.
- Field lines are always normal to the conducting surface.
- Field lines do not exist inside a conductor.
The explanation to this problem-can be done by keeping two things in mind.
(i) Concept of induction
(ii) The electric field lines interact with a conducting body normally.
Let us discuss the phenomenon of induction involved in this case. When a positive point charge is brought near an isolated conducting sphere without touching the sphere, then the free electrons in the sphere are attracted towards the positive charge.
Thus, the left surface of sphere has an excess of negative charge and the right surface of sphere has an excess of positive charge. It should be noted that both kinds of charges are bound in the metal sphere and cannot escape. They, therefore, reside on the surface of the sphere.
An electric field lines start from a positive point charge and ends at negative charge induced on the left surface of sphere. Also, electric field line emerges from a positive charge, in case of single charge and ends at infinity. Here, all these conditions are fulfilled in Fig. (i).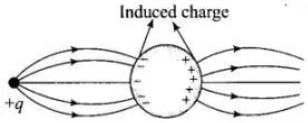
Q.3. The Electric flux through the surface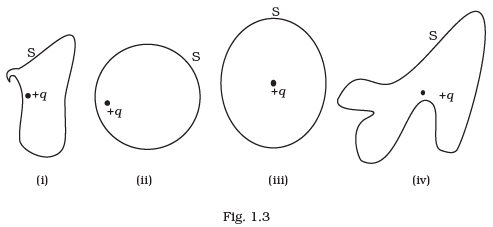 (a) In Fig.1.3 (iv) is the largest.
(a) In Fig.1.3 (iv) is the largest.
(b) In Fig. 1.3 (iii) is the least.
(c) In Fig. 1.3 (ii) is same as Fig. 1.3 (iii) but is smaller than Fig. 1.3 (iv)
(d) Is the same for all the figures.
Ans. (d)
Solution.
According to Gauss’ law of electrostatics, the total electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity,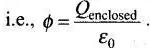
Thus, electric flux through a surface doesn’t depend on the shape, size or area of a surface but it depends on the amount of charge enclosed by the surface.
In given figures the charge enclosed are same that means the electric flux through all the surfaces should be the same.
Q.4. Five charges q1, q2, q3, q4, and q5 are fixed at their positions as shown in Fig. 1.4. S is a Gaussian surface. The Gauss’s law is given by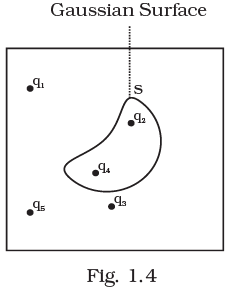
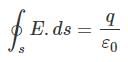 Which of the following statements is correct?
Which of the following statements is correct?
(a) E on the LHS of the above equation will have a contribution from q1, q5 and q3 while q on the RHS will have a contribution from q2 and q4 only.
(b) E on the LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q2 and q4 only.
(c) E on the LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q1, q3 and q5 only.
(d) Both E on the LHS and q on the RHS will have contributions from q2 and q4 only.
Ans. (b)
Solution.
According to Gauss’ law, the term qenclosed on the right side of the equation Фs E . dS = qenclosed / ϵ0 includes the sum of all charges enclosed by the surface called (Gaussian surface).
In left side equation, the electric field is due to all the charges present both inside as well as outside the Gaussian surface.
Hence in given question, E on LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q2 and q4 only.
Q.5. Figure 1.5 shows electric field lines in which an electric dipole p is placed as shown. Which of the following statements is correct?
(a) The dipole will not experience any force.
(b) The dipole will experience a force towards right.
(c) The dipole will experience a force towards left.
(d) The dipole will experience a force upwards.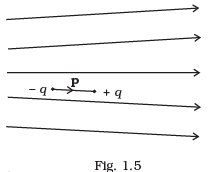 Ans. (c)
Ans. (c)
Solution.
If the lines of forces are equidistant and parallel straight lines, the field is uniform and if either lines of force are not equidistant, or straight line or both, the field will be non-uniform. The number of electric field lmes passing per unit area is proportional to the strength of electric field. For example, see the following figures: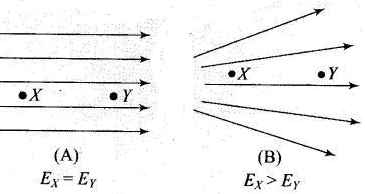 Hence in given question, from given pattern of electric field lines it is clear that the strength of electric field decreases from left to right. As a result force on charges also decreases from left to right.
Hence in given question, from given pattern of electric field lines it is clear that the strength of electric field decreases from left to right. As a result force on charges also decreases from left to right.
Here in given figure, the force on charge -q is greater than force on charge +q in turn dipole will experience a force towards left.
Q.6. A point charge +q, is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of the plane is
(a) Directed perpendicular to the plane and away from the plane.
(b) Directed perpendicular to the plane but towards the plane.
(c) Directed radially away from the point charge.
(d) Directed radially towards the point charge.
Ans. (a)
Solution.
If a point positive charge is placed near an isolated conducting plane, free electrons are attracted towards the positive charge. Result of this some negative charge develops on the surface of the plane towards the positive charge side and an equal positive charge develops on opposite side of the plane. The electric field lines are away from positive charge and perpendicular to the surface. Hence the field at a point P on the other side of the plane is directed perpendicular to the plane and away from the plane.
Q.7. A hemisphere is uniformly charged positively. The electric field at a point on a diameter away from the centre is directed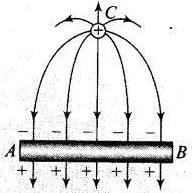 (a) Perpendicular to the diameter
(a) Perpendicular to the diameter
(b) Parallel to the diameter
(c) At an angle tilted towards the diameter
(d) At an angle tilted away from the diameter.
Ans. (a)
Solution.
In case of a uniformly positive charged hemisphere, if a point situated at a point on a diameter away from the centre, the electric field should be perpendicular to the diameter. In this case the component of electric field intensity parallel to the diameter cancel out.
MULTIPLE CHOICE QUESTIONS - II
Q.8. If  over a surface, then
over a surface, then
(a) The electric field inside the surface and on it is zero.
(b) The electric field inside the surface is necessarily uniform.
(c) The number of flux lines entering the surface must be equal to the number of flux lines leaving it.
(d) All charges must necessarily be outside the surface.
Ans. (c, d)
Solution.
We know electric flux is proportional to the number of electric field lines and the term Фs E . dS represents electric flux over the closed surface.
It means Фs E . dS represents the algebraic sum of number of flux lines entering the surface and number of flux lines leaving the surface.
If Фs E . dS = 0, this means the number of flux lines entering the surface must be equal to the number of flux lines leaving from it.
From Gauss’ law, we know Фs E . dS = q / ϵ0, here q is the charge enclosed by , the closed surface. If Фs E . dS = 0 then q = 0, i.e., net charge enclosed by the surface must be zero.
Hence all other charges must necessarily be outside the surface. This is because of the fact that charges outside the surface do not contribute to the electric flux.
Q.9. The Electric field at a point is
(a) Always continuous.
(b) Continuous if there is no charge at that point.
(c) Discontinuous only if there is a negative charge at that point.
(d) Discontinuous if there is a charge at that point.
Ans. (b, d)
Solution.
We cannot define electric field at the position of a charge, so we cannot say that electric field is always continuous. Hence option (a) is ruled out and option (d) is the correct choice. The electric field due to any charge will be continuous, if there is no other charge in the medium. It will be discontinuous if there is a charge at the point under consideration.
Q.10. If there were only one type of charge in the universe, then
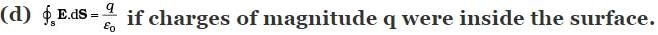
Ans. (b, d)
Solution.
From Gauss’ law, we know Фs E. dS =q / ϵ0, here q is the charge enclosed by the closed surface. If Фs E. dS= 0 then q = 0, i.e., net charge enclosed by the surface must be zero.
If the charge is outside the surface, then charge enclosed by the surface is q = 0 and thus, (j) Фs E. dS = 0.
Q.11. Consider a region inside which there are various types of charges but the total charge is zero. At points outside the region
(a) The electric field is necessarily zero.
(b) The electric field is due to the dipole moment of the charge distribution only.
(c) The dominant electric field is ∝ 1/r3,for large r, where r is the distance from
a origin in this region.
(d) The work done to move a charged particle along a closed path, away from the region, will be zero.
Ans. (c, d)
Solution.
From Gauss’ law, we know Фs E . dS =qenclosed / ϵ0. in left side equation.
the electric field is due to all the charges present both inside as well as outside the Gaussian surface. Hence if qenclosed= 0, it cannot be said that the electric field is necessarily zero.
If there are various types of charges in a region and total charge is zero, the region may be supposed to contain a number of electric dipoles.
Therefore, at points outside the region (may be anywhere w.r.t. electric dipoles), the dominant electric field ∝ 1/r3 for large r.
The electric field is conservative, work done to move a charged particle along a closed path, away from the region will be zero.
Q.12. Refer to the arrangement of charges in Fig. 1.6 and a Gaussian surface of radius R with Q at the centre. Then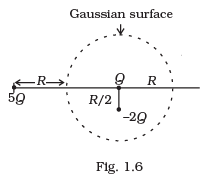 (a) Total flux through the surface of the sphere is -Q/εo.
(a) Total flux through the surface of the sphere is -Q/εo.
(b) Field on the surface of the sphere is -Q/4πε0R2.
(c) Flux through the surface of sphere due to 5Q is zero.
(d) Field on the surface of sphere due to –2Q is same everywhere.
Ans. (a) and (c)
Solution.
(a) Is true by Gauss’s law. Here net charge = -2Q + Q.
(b) Is the electric field on a conducting sphere. There is no any conducting sphere but only surface or spherical space is there.
(c) 5Q charge outside the Gaussian surface will not contribute to electric flux in Gaussian surface (or space).
For (d), the distance of Gaussian surface from -2Q is different, so field will not be same on the surface.
Q.13. A positive charge Q is uniformly distributed along a circular ring of radius R. A small test charge q is placed at the centre of the ring (Fig. 1.7). Then
(a) If q > 0 and is displaced away from the centre in the plane of the ring, it will be pushed back towards the centre.
(b) If q < 0 and is displaced away from the centre in the plane of the ring, it will never return to the centre and will continue moving till it hits the ring.
(c) If q < 0, it will perform SHM for small displacement along the axis.
(d) Q at the centre of the ring is in an unstable equilibrium within the plane of the ring for q > 0.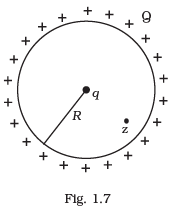 Ans. (a, b, c, d)
Ans. (a, b, c, d)
Solution.
The positive charge Q is uniformly distributed along the circular ring then electric field at the centre of ring will be zero, hence no force is experienced by the charge if it is placed at the centre of the ring.
Now the charge is displaced away from the centre in the plane of the ring. There will be net electric field opposite to displacement will push back the charge towards the centre of the ring if the charge is positive. If charge is negative, it will experience net force in the direction of displacement and the charge will continue moving till it hits the ring. Also this negative charge is in an unstable equilibrium. Hence options (a), (b) and (d) are correct.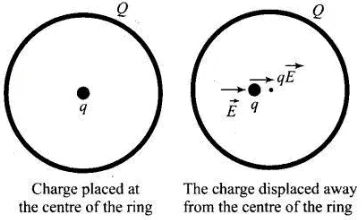
 The direction of electric field on the axis of a positively charged ring is along the axis of the ring and away from the centre of ring. If a negative charge is shifted away from the centre along the axis of ring, charge will experience a net force towards the centre and return to the centre and will perform SHM for small displacement along the axis.
The direction of electric field on the axis of a positively charged ring is along the axis of the ring and away from the centre of ring. If a negative charge is shifted away from the centre along the axis of ring, charge will experience a net force towards the centre and return to the centre and will perform SHM for small displacement along the axis.
VERY SHORT ANSWER TYPE QUESTIONS
Q.14. An arbitrary surface encloses a dipole. What is the electric flux through this surface?
Ans. From Gauss’s theorem, Electric flux,
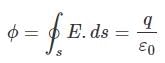
Net charge inside the Gaussian surface due to a dipole = +q - q = 0
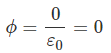
Q.15. A metallic spherical shell has an inner radius R1 and outer radius R2. A charge Q is placed at the centre of the spherical cavity. What will be surface charge density on
(i) The inner surface, and
(ii) The outer surface?
Ans. A charge Q is placed at the centre of the spherical cavity. So, the charge induced at the inner surface of the sphere will be -Q and at outer surface of the sphere is +Q. The Surface charge density on the inner surface σ1 = Charge/Area = -Q/4πR12
The Surface charge density on the inner surface σ1 = Charge/Area = -Q/4πR12
Surface charge density on the outer surface σ2 = + Q/4πR22
Hence,
(i) =-Q/4πR12
(ii) + Q/4πR22
Q.16. The dimensions of an atom are of the order of an Angstrom. Thus there must be large electric fields between the protons and electrons. Why, then is the electrostatic field inside a conductor zero?
Ans. In any neutral atom, the number of electrons and protons are equal, and the protons and electrons are bound into an atom with distinct and independent existence. Electrostatic fields are caused by the presence of excess charges. But there can be no excess charge on the inter-surface of an isolated conductor. So, the electrostatic fields inside a conductor is zero despite the fact that the dimensions of an atom are of the order of an Angstrom.
Q.17. If the total charge enclosed by a surface is zero, does it imply that the electric field everywhere on the surface is zero? Conversely, if the electric field everywhere on a surface is zero, does it imply that net charge inside is zero.
Ans. According to Gauss’ law, the flux associated with any closed surface is given by Фs E . dS =qenclosed /ϵ0. The term qenclosed on the right side of the equation includes the sum of all charges enclosed by the surface called (Gaussian surface).
In left side equation,the electric field is due to all the charges present both inside as well as outside the Gaussian surface.
Thus, despite being total charge enclosed by a surface zero, it doesn’t imply that the electric field everywhere on the surface is zero, the field may be normal to the surface.
Also, conversely if the electric field everywhere on a surface is zero.
Q.18. Sketch the electric field lines for a uniformly charged hollow cylinder shown in Fig 1.8.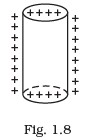 Ans. The electric field lines starts from positive charges and move towards infinity and meet plane surface normally as shown in the figure below:
Ans. The electric field lines starts from positive charges and move towards infinity and meet plane surface normally as shown in the figure below: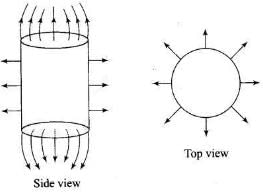 Important point: No electric field lines will be present inside the cylinder because of electrostatic shielding. Electrostatic shielding/screening is the phenomenon of protecting a certain region of space from external electric field. Sensitive instruments and appliances are affected seriously with strong external electrostatic fields. Their working suffers and they may start misbehaving under the effect of unwanted fields.
Important point: No electric field lines will be present inside the cylinder because of electrostatic shielding. Electrostatic shielding/screening is the phenomenon of protecting a certain region of space from external electric field. Sensitive instruments and appliances are affected seriously with strong external electrostatic fields. Their working suffers and they may start misbehaving under the effect of unwanted fields.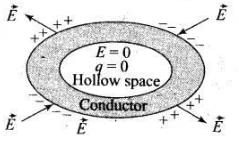 The electrostatic shielding can be achieved by protecting and enclosing the sensitive instruments inside a hollow conductor because inside hollow conductors, electric fields is zero.
The electrostatic shielding can be achieved by protecting and enclosing the sensitive instruments inside a hollow conductor because inside hollow conductors, electric fields is zero.
Q.19. What will be the total flux through the faces of the cube (Fig. 1.9) with side of length a if a charge q is placed at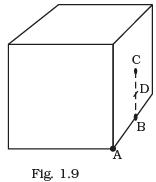 (a) A: a corner of the cube.
(a) A: a corner of the cube.
(b) B: mid-point of an edge of the cube.
(c) C: centre of a face of the cube.
(d) D: mid-point of B and C.
Ans.
(a) Use of symmetry consideration may be useful in problems of flux calculation. We can imagine the charged particle is placed at the centre of a cube of side 2a. We can observe that the charge is being shared equally by 8 cubes. Therefore, total flux through the faces of the given cube =q/8ϵ0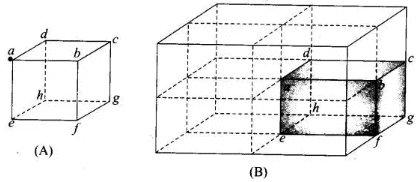 (b) If the charge q is placed at B, middle point of an edge of the cube, it is being shared equally by 4 cubes. Therefore, total flux through the faces of the given cube = q/4ϵ0
(b) If the charge q is placed at B, middle point of an edge of the cube, it is being shared equally by 4 cubes. Therefore, total flux through the faces of the given cube = q/4ϵ0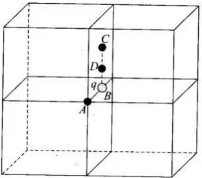 (c) If the charge q is placed at C, the centre of a face of the cube, it is being shared equally by 2 cubes. Therefore, total flux through the faces of the given cube =q/2ϵ0
(c) If the charge q is placed at C, the centre of a face of the cube, it is being shared equally by 2 cubes. Therefore, total flux through the faces of the given cube =q/2ϵ0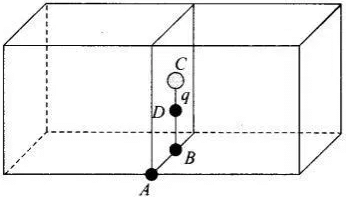 (d) Finally, if charge q is placed at D, the mid-point of B and C, it is being shared equally by 2 cubes. Therefore, total flux through the faces of the given cube =q/2ϵ0
(d) Finally, if charge q is placed at D, the mid-point of B and C, it is being shared equally by 2 cubes. Therefore, total flux through the faces of the given cube =q/2ϵ0
SHORT ANSWER TYPE QUESTIONS
Q.20. A paisa coin is made up of Al-Mg alloy and weighs 0.75 g. It has a square shape and its diagonal measures 17 mm. It is electrically neutral and contains equal amounts of positive and negative charges.
Treating the paisa coins made up of only Al, find the magnitude of equal number of positive and negative charges. What conclusion do you draw from this magnitude?
Ans. A 0.75 g paisa coin now is made with Al only.
So, the mass of a paisa coin = 0.75g
Atomic mass of Al ≅ 27 a.m.u
So, number of moles in 0.75 g = 0.75/27 mole
Number of Al atoms in coin =N
= 0.75/27 x 6.022 x 1023 atoms
Atomic number of Al= 13
∴ Number of electrons (negative charge) and protons (positive charge) =13.
So, number of either proton or electron in a coin
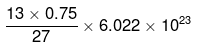
Magnitude of charge on a proton or electron =1.6 x 10-19 C
So, total charge (either positive or negative)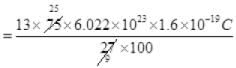
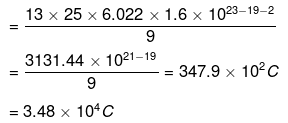
Either positive or negative charge on a coin= 34.8 KC
It concludes that even a 0.75 g Al contains an enormous amount of positive and negative charges and equal in magnitude.
Q.21. Consider a coin of Example 1.20. It is electrically neutral and contains equal amounts of positive and negative charge of magnitude 34.8 kC. Suppose that these equal charges were concentrated in two point charges seperated by
(i) 1 cm (~1/2 x diagonal of the one paisa coin),
(ii) 100 m (~ length of a long building), and
(iii) 106 m (radius of the earth).
Find the force on each such point charge in each of the three cases. What do you conclude from these results?
Ans. We know force between two point charges separated at a distance r,
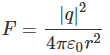
Here,
q = ± 34.8 kC = ±3.48 x 104 C
r1 = 1 cm = 10-2 m, r2 = 100m, r3 = 106 m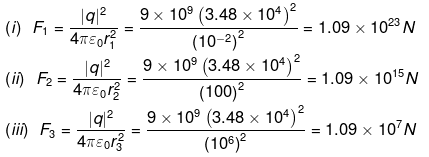
Conclusion: Here we can observe that when positive and negative charges in ordinary neutral matter are separated as point charges, they exert very large force. It means, it is very difficult to disturb electrical neutrality of matter.
Q.22. Fig. 1.10 represents a crystal unit of cesium chloride, CsCl. The cesium atoms, represented by open circles are situated at the corners of a cube of side 0.40 nm, whereas a Cl atom is situated at the centre of the cube. The Cs atoms are deficient in one electron while the Cl atom carries an excess electron.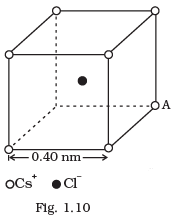 (i) What is the net electric field on the Cl atom due to eight Cs atoms?
(i) What is the net electric field on the Cl atom due to eight Cs atoms?
(ii) Suppose that the Cs atom at the corner A is missing. What is the net force now on the Cl atom due to seven remaining Cs atoms?
Ans.
(i) The cesium atoms, are situated at the comers of a cube and Cl atom is situated at the centre of the cube. From the given figure, we can analyse that the chlorine atom is at equal distance from all the eight comers of cube where cesium atoms are placed. Thus, due to symmetry the electric field due to all Cs atoms, on Cl atom will cancel out. Hence net electric field at the centre of cube is zero.
(ii) We define force on a charge particle due to external electric field as F = qE. If eight cesium atoms, are situated at the comers of a cube, the net force on Cl atom is situated at the centre of the cube will be zero as net electric field at the centre of cube is zero. We can write that the vector sum of electric field due to charge A and electric field due to other seven charges at the centre of cube should be zero or, EA + Eseven charges= 0
Hence,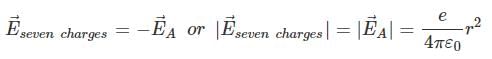
Thus, net force on Cl atom at A would be,
F = eEseven charge = e2/4πε0r2
where, r = distance between Cl ion and Cs ion.
Here,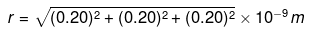
= 0.346 x 10-9 m
Now,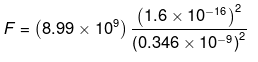
= 1.92 x 10-9 N, direct from A to Cl-
Q.23. Two charges q and –3q are placed fixed on x-axis separated by distance ‘d’. Where should a third charge 2q be placed such that it will not experience any force?
Ans. The force on any charge will be zero only if net electric field at the position of charge is zero. Let electric field is zero at a distance x from charge q.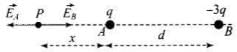
At point P,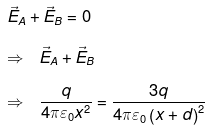
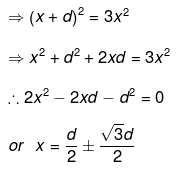
(Negative sign lies between q and - 3q and hence is unadaptable.)
Hence,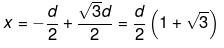
Hence if charge 2q is placed at a distance d/2(1 + √3) to the left of q.
Q.24. Fig. 1.11 shows the electric field lines around three point charges A, B and C.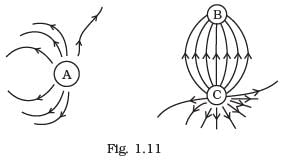 (a) Which charges are positive?
(a) Which charges are positive?
(b) Which charge has the largest magnitude? Why?
(c) In which region or regions of the picture could the electric field be zero? Justify your answer.
(i) near A,
(ii) near B,
(iii) near C,
(iv) nowhere.
Ans.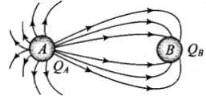
(i) The number of lines originating or terminating on a charge is proportional to the magnitude of charge. In the following figure electric lines of force are originating from A and terminating at B, hence QA is positive while QB is negative. Also number of electric lines at force linked with QA are more than those linked with QB, hence |QA| > |QB|.
(ii) The electric lines of forces always starts from a positive charge and ends at a negative charge. In case of a single isolated charge, electric lines of force start from positive charge ends at infinity. There is no neutral point between unlike charges. Point between two like charges where electrostatic force is zero is called neutral point. A neutral point may exist between two like charges. Also between two like charges the neutral point is closer to the charge with smaller magnitude.
(a) Here, in the figure, the electric lines of force starts from A and C.
Therefore, charges A and C must be positive.
(b) The number of electric lines of forces starting from charge C are maximum, so C must have the largest magnitude.
(c) From the figure we see that a neutral point exists between charges A and C. Here, more number of electric lines of forces shows higher strength of charge C than A. Thus, electric field is zero near charge A hence neutral point lies near A.
Q.25. Five charges, q each are placed at the corners of a regular pentagon of side ‘a’ (Fig. 1.12).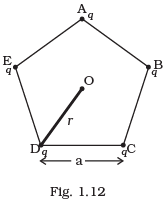 (a)
(a)
(i) What will be the electric field at O, the centre of the pentagon?
(ii) What will be the electric field at O if the charge from one of the corners (say A) is removed?
(iii) What will be the electric field at O if the charge q at A is replaced by –q?
(b) How would your answer to (a) be affected if pentagon is replaced by n-sided regular polygon with charge q at each of its corners?
Ans. (a)
(i) Point O is symmetric to all the five equal charges of +q placed at vertices of the regular polygon. So net electric field will be zero at O.
(ii) When a charge q from A is removed from symmetric charge distribution about ‘O’, the net electric field due to rest of the charges will be equal in magnitude as there is -q charge at ‘A’. So Electric field at ‘O’ in this case
E1 = -1q/4πε0r2
The direction of E is from O to A.
(iii) When the charge q from A is removed and -q charge is placed then electric field of at O
When a new charge -q is placed the E.F. will increase by -q/4πε0r2
Now the resultant becomes
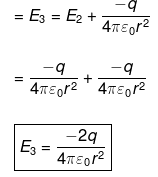
(b) Now when Pentagon is replaced by the n-sided polygon
(i) electric field at ‘O’ will be again zero as all charge distribution about O is symmetric as in the case of the electric field at the centre of conducting ring or shell.
(ii) The electric field at O will remain same as in an (ii) if a charge q is removed. The resultant will be equal to the electric field due to charge -q at A.
So, the electric field at ‘O’ at the centre of a regular polygon of n side if a charge from one vertex is removed is equal to 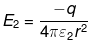 . The direction from O is opposite to OA.
. The direction from O is opposite to OA.
(iii) If charge -q is placed at one vertex after removing +q from there then resultant electric field at ‘O’ will be due to charge (-2q) at A.
So the net electric field at O after removing q from A by placing -q at A.
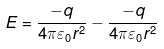
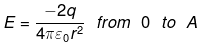
LONG ANSWER TYPE QUESTIONS
Q.26. In 1959 Lyttleton and Bondi suggested that the expansion of the Universe could be explained if matter carried a net charge.
Suppose that the Universe is made up of hydrogen atoms with a number density N, which is maintained a constant. Let the charge on the proton be: ep = – (1 + y)e where e is the electronic charge.
(a) Find the critical value of y such that expansion may start.
(b) Show that the velocity of expansion is proportional to the distance from the centre.
Ans.
(a) Consider that the Universe is spherical with radius R made up of H atoms.
Charge on proton = -(1+y)e
So the total charge on H atom i.e eH = ep+e
= -(1+y)e+e
= [-1-y+1]e
Charge on 1 H atom =-ye
The number of H atoms in spherical Universe = N.V.
= N. 4/3πR3
∴ The net charge in Universe = N. 4/3πR3(-ye)
Consider the boundaries of Universe as Gaussian surface then by Gauss’s law of electrostatics,
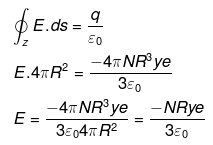
Electrostatic force or Columb force acting on one H atom Fc = qE
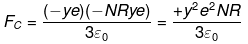
Positive sign Fc shows repulsive force.
We know, gravitational potential at boundary of Universe = GM/R2
M=mass of Universe (or all H atoms)
So, the gravitational force acting on H atom at boundary of Universe = Gravitational potential x m [m=mass of H-atom]
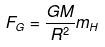
Mass of 1H atom = mass of a proton
=mp
Mass of Universe(M)= No. of H atoms in Universe x mp
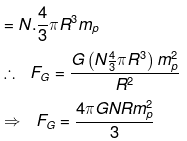
If Fc > Fg> then the universe will start to expand. So for critical value of expansion of y would be when
FC = FG
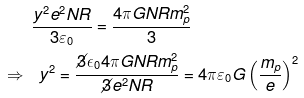
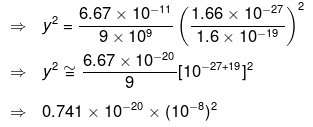
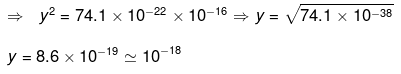
So critical value of y is of the order of 10-18 so that Universe start to expand.
(b) For expansion repulsive force Fc must be greater than, attractive gravitational force So net force on H atom to expand
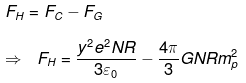
This force FH will produce acceleration in H atom
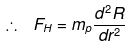
Here R (size of Universe) changes with time as Universe expands with velocity
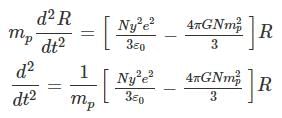
As N, y,e,∈0 , n, G, mp are constants so taking a new constant α2 such that
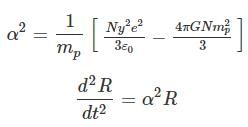
It is a differential equation of order 2. Its solution is
R = Aeαt + Be-αt
For expansion of Universe B = 0
∴ R = Aeαt
Receding velocity of Universe v = dR/dt
v = Aαeαt or v = Rα
As α is constant. So the receding (expanding) velocity of Universe is directly proportional to the distance of matter (H atom) from the centre of Universe.
Q.27. Consider a sphere of radius R with charge density distributed as
ρ(r) = kr (for r < R)
ρ(r) = 0 (for r>R) .
(a) Find the electric field at all points r.
(b) Suppose the total charge on the sphere is 2e where e is the electron charge. Where can two protons be embedded such that the force on each of them is zero. Assume that the introduction of the proton does not alter the negative charge distribution.
Ans.
(a) Consider a sphere (solid) of radius R with charge density ρ (r)=kr (for r>R) and ρ (r)=0 (for r >R)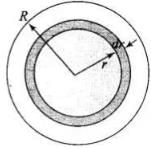 Case-I: Consider the Gaussian surface at radius r < R. Applying Gaussian law at A
Case-I: Consider the Gaussian surface at radius r < R. Applying Gaussian law at A
v = Volume of Gaussian surface
∴ q = ρ(r). 4/3 πr3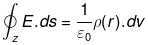
v = 4/3 πr3
dv = 4/3 π3r2dr = 4 πr2 dr
ρ (r)=kr for r<R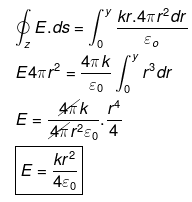
As the field is positive so the direction of E is radially outward.
Case-II: Consider a Gaussian surface of radius r>R As charge inside the Gaussian surface is up to r= 0 to r = R remains same as earlier. So, net charge in this Gaussian surface
As charge inside the Gaussian surface is up to r= 0 to r = R remains same as earlier. So, net charge in this Gaussian surface
q=ρ(r).dv
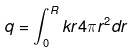
as charge reside upto radius R only
By Gaussian law,
As,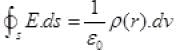
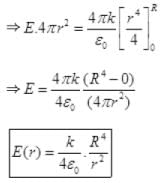
The direction of electric field is radially outward.
(b) As the total negative charge on the sphere is 2e (e is the charge on the electron) is distributed in a sphere of radius R symmetrically. So two protons must be symmetrical in the sphere. i.e., two protons must be on the opposite sides equidistant from the centre as shown in fig.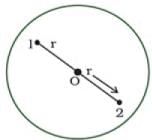 Charge on sphere q = p(r)dv
Charge on sphere q = p(r)dv
From last part (a) dv = 4πr2.dr
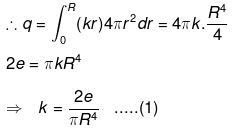
Protons 1 and 2 shown in fig. are embedded at distance r from centre O, of the sphere, thus the force of attraction between a proton and negative charge distribution in a sphere as E is due to (-) charge. Electric field due to charge distribution inside the charged sphere at r<R from part (a) is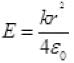
The protons 1 & 2 are embedded at distance r from the centre of the sphere, the attractive force on proton 1 due to charge distribution is: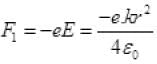
Repulsive force on proton 1 due to proton 2 = F2 by Coulomb’s law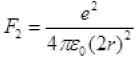
Net force on proton 1, F = F1 + F2 = 0
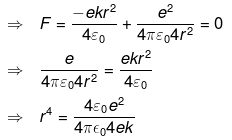
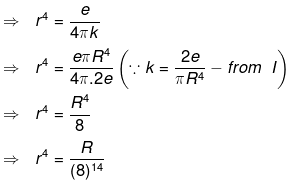
So protons must be embedded at a distance of R/(8)1/4 from the centre of the sphere of radius R.
Q.28. Two fixed, identical conducting plates (α & β), each of surface area S are charged to –Q and q, respectively, where Q > q > 0. A third identical plate (γ), free to move is located on the other side of the plate with charge q at a distance d (Fig 1.13). The third plate is released and collides with the plate β . Assume the collision is elastic and the time of collision is sufficient to redistribute charge amongst β &γ .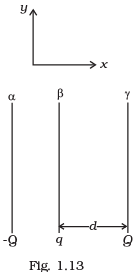 (a) Find the electric field acting on the plate γ before collision.
(a) Find the electric field acting on the plate γ before collision.
(b) Find the charges on β and γ after the collision.
(c) Find the velocity of the plate γ after the collision and at a distance d from the plate β.
Ans.
(a) As the plate y has Q charge. So, electric field on plate y due to plate α
Eα = σ/2ε0 = -Q/2Sε0
E∞ = -Q/2Sεo towards left
Similarly, an electric field on y due to plate β = Eβ = +q/2Sε0 towards the right.
So, this net electric field on plate γ = E = Fα + Eβ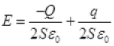

So, the electric field on plate y before the collision is towards left as (|Q>|q|)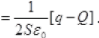
(b) On collision between plate β and y, their potential becomes same. Suppose during the collision at any point P between plates p and y the charges on β and y plates are q1 and q2 respectively. Consider a point 0 to the right of plate B and left to plate γ such that net electric field at 0 is zero.
Electric field due to plate α at 0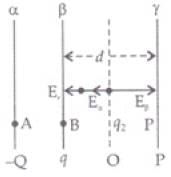 Electric field due to plate a at 0 = -Q/2Sε0 (towards left)
Electric field due to plate a at 0 = -Q/2Sε0 (towards left)
Electric field at O due to plate β = +q1/2Sε0 (towards right)
Electric field at O due to plate γ
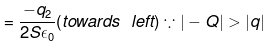
Net electric field at O must be zero so,
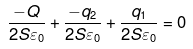
Or Q=q1 - q2 … I
As there is no loss of charge on collision by law of conversation of charges so,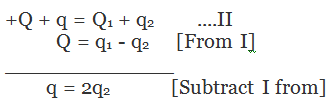
Or q2 = q/2
So, charge on plate y after collision = q/2 unit.
Charge on plate β = Q + q - q/2
⇒ Charge on plate β = Q+ q/2
(c) After the collision of plate γ with β and after charge distribution between plate γ and β, the plates will repel each other and plate γ will move towards its initial position as plate γ is free to move but plate, α β are fixed.
Let the velocity of plate γ after the collision at distance d is v and mass of plate is m, then gain in KE round the trip from P to B and B to P must be equal to the work done by the electric field.
After collision, the electric field on plate y at 0, due to plate at a and p
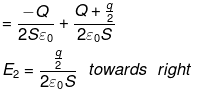
Electric field on plate y just before collision due to plate, α and β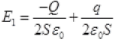
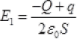
Force on plate γ just before collision = E1Q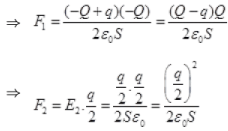
W = (F1+F2)d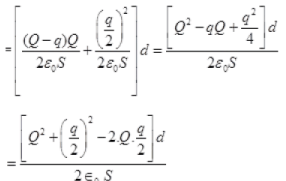
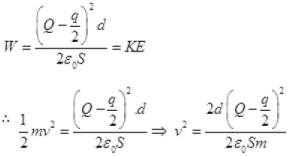
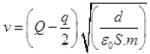
is the velocity of plate y at a distance d after the collision.
Q.29. There is another useful system of units, besides the SI/mks A system, called the cgs (centimeter-gram-second) system. In this system Coloumb’s law is given by
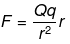
where the distance r is measured in cm (= 10-2 m), F in dynes (=10-5 N) and the charges in electrostatic units (es units), where 1 es unit of charge = 1/[3] x 10-9C
The number [3] actually arises from the speed of light in vaccum which is now taken to be exactly given by c = 2.99792458 × 108 m/s. An approximate value of c then is c = [3] × 108 m/s.
(i) Show that the coloumb law in cgs units yields
1 esu of charge = 1 (dyne)1/2 cm.
Obtain the dimensions of units of charge in terms of mass M, length L and time T. Show that it is given in terms of fractional powers of M and L.
(ii) Write 1 esu of charge = x C, where x is a dimensionless number.
Show that this gives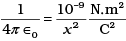
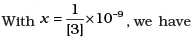
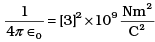
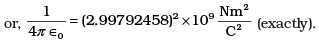
Ans.
(i) F = Qq/r2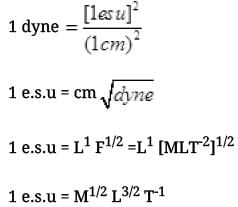
So e.s.u of charge is represented in terms of fractional powers of 1/2 of M, 3/2 of L and (-1) of T
(ii)1 e.s.u = x C [Given]
Where, x is a dimensionless number. The Columbian force between two charges each of magnitude 1 e.s.u separated by 1 cm is one dyne =10-5N. This situation is equivalent to two charges of magnitude x C separated by 10-2m. By Coulomb’s law,
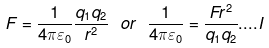
q1= q2= x C
r = 1 cm = 10-2 m
If F= 1 dyne,
From I,

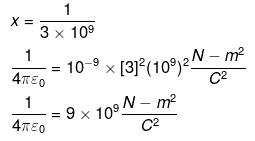
If [3] → 2.99792458 we get
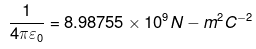
Q.30. Two charges –q each are fixed separated by distance 2d. A third charge q of mass m placed at the mid-point is displaced slightly by x (x<<d) perpendicular to the line joining the two fixed charged as shown in Fig. 1.14. Show that q will perform simple harmonic oscillation of time period.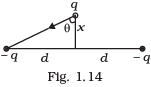

Ans.
Force acting on charge q due to -q at A will be FPA along P to A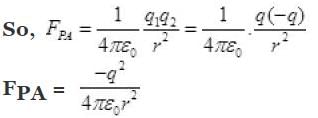
Similarly,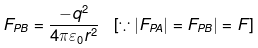
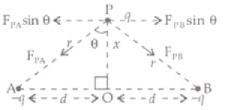
So, the horizontal components of FPA and FPB are equal and opposite so neutralise each other. The vertical components of FPA and FPB are downward and so add up.
Net force on q at P= FpB cos θ + FPA cos θ = 2F cos θ
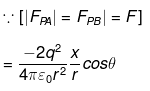
Force on q downwards
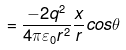
r2=x2+d2 [by Pythagoras theorem]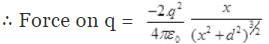
∵ x<<<d ∴ x2<<<<d2
As negative sign shows force of attraction.
So net force on q at P downwards
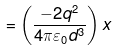
So the force on q is directly proportional to the displacement from mean position O ( the midpoint of the segment joining -q and -q charges). So the motion of q about O will be S.H.M.
F = -kx where,
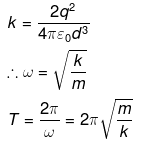
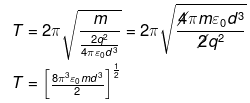
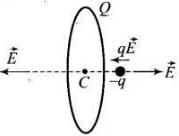
Q.31. Total charge –Q is uniformly spread along length of a ring of radius R. A small test charge +q of mass m is kept at the centre of the ring and is given a gentle push along the axis of the ring.
(a) Show that the particle executes a simple harmonic oscillation.
(b) Obtain its time period.
Ans.
(a) As -Q charge is equally distributed along a conducting ring, so, at the point O, the centre of ring is symmetric to charge distribution. So the electric field at O will be zero, or force on charge q placed at 0 will be equal to qE i.e., qx 0=0.
But when the charge q is displaced gently from ‘O’, or mean position the electric field on q will not be zero so force acts on q as in fig. below.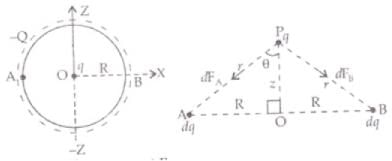 Force on q at P when z is small
Force on q at P when z is small
F = FA+FB 
FY = FAcos θ+ FA cosθ
FY = 2FA cos θ(downward)
The horizontal component of FA and FB will be equal and opposite, so cancelled out. So net force acting on q due to small element dl of ring = dF cos θ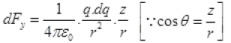
Charge on small element dl of ring
dq= λ dl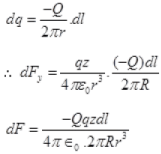
Integrating both sides we get,
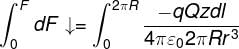
[if z<<<R,z2<<<<R2 or z2 can be neglected]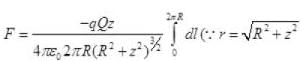
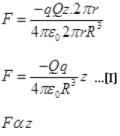
So motion of q is SHM
F = -kz...[II]
(b)
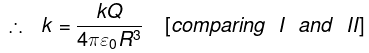
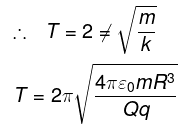
|
201 videos|410 docs|280 tests
|






















