Structure of Atom - 2 NCERT Solutions - RRB Group D / RPF Constable PDF Download
Ques 2.26: An atom of an element contains 29 electrons and 35 neutrons. Deduce
(i) the number of protons and
(ii) the electronic configuration of the element.
Ans:-
(i) For an atom to be neutral, the number of protons is equal to the number of electrons.
∴ Number of protons in the atom of the given element = 29
(ii) The electronic configuration of the atom is
1s2 2s2 2p6 3s2 3p6 4s2 3d10.
Ques 2.27: Give the number of electrons in the species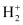 , H2 and
, H2 and 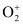
Ans:-
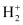 :
:
Number of electrons present in hydrogen molecule (H2) = 1 + 1 = 2
∴ Number of electrons in 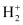 = 2 – 1 = 1
= 2 – 1 = 1
H2:
Number of electrons in H2 = 1 + 1 = 2
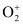 :
:
Number of electrons present in oxygen molecule (O2) = 8 + 8 = 16
∴ Number of electrons in 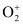 = 16 – 1 = 15
= 16 – 1 = 15
Ques 2.28: (i) An atomic orbital has n = 3. What are the possible values of l and ml ?
(ii) List the quantum numbers (ml and l) of electrons for 3d orbital.
(iii) Which of the following orbitals are possible?
1p, 2s, 2p and 3f
Ans:-
(i) n = 3 (Given)
For a given value of n, l can have values from 0 to (n – 1).
∴ For n = 3
l = 0, 1, 2
For a given value of l, ml can have (2l 1) values.
For l = 0, m = 0
l = 1, m = – 1, 0, 1
l = 2, m = – 2, – 1, 0, 1, 2
∴ For n = 3
l = 0, 1, 2
m0 = 0
m1 = – 1, 0, 1
m2 = – 2, – 1, 0, 1, 2
(ii) For 3d orbital, l = 2.
For a given value of l, mlcan have (2l 1) values i.e., 5 values.
∴ For l = 2
m2 = – 2, – 1, 0, 1, 2
(iii) Among the given orbitals only 2s and 2p are possible. 1p and 3f cannot exist.
For p-orbital, l = 1.
For a given value of n, l can have values from zero to (n – 1).
∴ For l is equal to 1, the minimum value of n is 2.
Similarly,
For f-orbital, l = 4.
For l = 4, the minimum value of n is 5.
Hence, 1p and 3f do not exist.
Ques 2.29: Using s, p, d notations, describe the orbital with the following quantum numbers.
(a) n = 1, l = 0,
(b) n = 3; l =1,
(c) n = 4; l = 2,
(d) n = 4; l =3.
Ans:- (a) n = 1, l = 0 (Given)
The orbital is 1s.
(b) For n = 3 and l = 1
The orbital is 3p.
(c) For n = 4 and l = 2
The orbital is 4d.
(d) For n = 4 and l = 3
The orbital is 4f.
Ques 2.30: Explain, giving reasons, which of the following sets of quantum numbers are not possible.
(a) n = 0, l = 0, ml = 0, 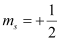
(b) n = 1, l = 0, ml = 0,
(c) n = 1, l = 1, ml = 0, 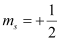
(d) n = 2, l = 1, ml = 0, 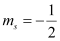
(e) n = 3, l = 3, ml = – 3, 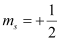
(f) n = 3, l = 1, ml = 0, 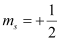
Ans:-
(a) The given set of quantum numbers is not possible because the value of the principal quantum number (n) cannot be zero.
(b) The given set of quantum numbers is possible.
(c) The given set of quantum numbers is not possible.
For a given value of n, ‘l’ can have values from zero to (n – 1).
For n = 1, l = 0 and not 1.
(d) The given set of quantum numbers is possible.
(e) The given set of quantum numbers is not possible.
For n = 3,
l = 0 to (3 – 1)
l = 0 to 2 i.e., 0, 1, 2
(f) The given set of quantum numbers is possible.
Ques 2.31: How many electrons in an atom may have the following quantum numbers?
(a) n = 4, 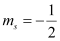
(b) n = 3, l = 0
Ans:-
(a) Total number of electrons in an atom for a value of n = 2n2
∴ For n = 4,
Total number of electrons = 2 (4)2 = 32
The given element has a fully filled orbital as
1s2 2s2 2p6 3s2 3p6 4s2 3d10.
Hence, all the electrons are paired.
∴ Number of electrons (having n = 4 and 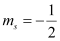 ) = 16
) = 16
(b) n = 3, l = 0 indicates that the electrons are present in the 3s orbital. Therefore, the number of electrons having n = 3 and l = 0 is 2.
Ques 2.32: Show that the circumference of the Bohr orbit for the hydrogen atom is an integral multiple of the de Broglie wavelength associated with the electron revolving around the orbit.
Ans:- Since a hydrogen atom has only one electron, according to Bohr’s postulate, the angular momentum of that electron is given by:
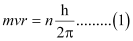
Where, n = 1, 2, 3, …
According to de Broglie’s equation:
Substituting the value of ‘mv’ from expression (2) in expression (1):
Since ‘2πr’ represents the circumference of the Bohr orbit (r), it is proved by equation (3) that the circumference of the Bohr orbit of the hydrogen atom is an integral multiple of de Broglie’s wavelength associated with the electron revolving around the orbit.
Ques 2.33: What transition in the hydrogen spectrum would have the same wavelength as the Balmer transition n = 4 to n = 2 of He spectrum?
Ans:- For He+ ion, the wave number 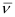 associated with the Balmer transition, n = 4 to n = 2 is given by:
associated with the Balmer transition, n = 4 to n = 2 is given by:
Where,
n1 = 2, n2 = 4
Z = atomic number of helium
According to the question, the desired transition for hydrogen will have the same wavelength as that of He+ .
By hit and trail method, the equality given by equation (1) is true only when n1 = 1and n2 = 2.
∴ The transition for n2 = 2 to n = 1 in hydrogen spectrum would have the same wavelength as Balmer transition n = 4 to n = 2 of He+ spectrum.
Ques 2.34: Calculate the energy required for the process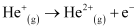 The ionization energy for the H atom in the ground state is 2.18 ×10–18 J atom–1
The ionization energy for the H atom in the ground state is 2.18 ×10–18 J atom–1
Ans:- Energy associated with hydrogen-like species is given by,

For the given process,
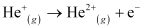
An electron is removed from n = 1 to n = ∞.
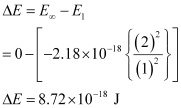
∴ The energy required for the process 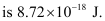
Ques 2.35: If the diameter of a carbon atom is 0.15 nm, calculate the number of carbon atoms which can be placed side by side in a straight line across length of scale of length 20 cm long.
Ans:- 1 m = 100 cm
1 cm = 10–2 m
Length of the scale = 20 cm
= 20 × 10–2 m
Diameter of a carbon atom = 0.15 nm
= 0.15 × 10–9 m
One carbon atom occupies 0.15 × 10–9 m.
∴ Number of carbon atoms that can be placed in a straight line
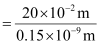
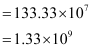
Question 2.36: 2 × 108 atoms of carbon are arranged side by side. Calculate the radius of carbon atom if the length of this arrangement is 2.4 cm.
Ans:- Length of the given arrangement = 2.4 cm
Number of carbon atoms present = 2 × 108
∴ Diameter of carbon atom

Question 2.37: The diameter of zinc atom is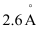 .Calculate (a) radius of zinc atom in pm and (b) number of atoms present in a length of 1.6 cm if the zinc atoms are arranged side by side lengthwise.
.Calculate (a) radius of zinc atom in pm and (b) number of atoms present in a length of 1.6 cm if the zinc atoms are arranged side by side lengthwise.
Ans:- (a) Radius of zinc atom = diameter/2
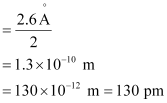
(b) Length of the arrangement = 1.6 cm
= 1.6 × 10–2 m
Diameter of zinc atom = 2.6 × 10–10 m
∴ Number of zinc atoms present in the arrangement
Question 2.38: A certain particle carries 2.5 × 10–16C of static electric charge. Calculate the number of electrons present in it.
Ans:- Charge on one electron = 1.6022 × 10–19 C
⇒ 1.6022 × 10–19C charge is carried by 1 electron.
∴ Number of electrons carrying a charge of 2.5 × 10–16 C
Question 2.39: In Milikan’s experiment, static electric charge on the oil drops has been obtained by shining X-rays. If the static electric charge on the oil drop is –1.282 × 10–18C, calculate the number of electrons present on it.
Ans:- Charge on the oil drop = 1.282 ×10–18C
Charge on one electron = 1.6022 × 10–19C
∴Number of electrons present on the oil drop
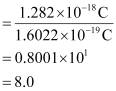
Question 2.40: In Rutherford’s experiment, generally the thin foil of heavy atoms, like gold, platinum etc. have been used to be bombarded by the α-particles. If the thin foil of light atoms like aluminium etc. is used, what difference would be observed from the above results?
Ans:- A thin foil of lighter atoms will not give the same results as given with the foil of heavier atoms. Lighter atoms would be able to carry very little positive charge. Hence, they will not cause enough deflection of α-particles (positively charged).
Question 2.41: Symbols 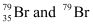 can be written, whereas symbols
can be written, whereas symbols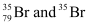 are not acceptable. Answer briefly.
are not acceptable. Answer briefly.
Ans:- The general convention of representing an element along with its atomic mass (A) and atomic number (Z) is 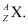
Hence,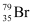 is acceptable but
is acceptable but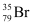 is not acceptable.
is not acceptable.
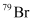 can be written but
can be written but 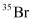 cannot be written because the atomic number of an element is constant, but the atomic mass of an element depends upon the relative abundance of its isotopes. Hence, it is necessary to mention the atomic mass of an element
cannot be written because the atomic number of an element is constant, but the atomic mass of an element depends upon the relative abundance of its isotopes. Hence, it is necessary to mention the atomic mass of an element
Question 2.42: An element with mass number 81 contains 31.7% more neutrons as compared to protons. Assign the atomic symbol.
Ans:- Let the number of protons in the element be x.
∴ Number of neutrons in the element
= x + 31.7% of x
= x + 0.317 x
= 1.317 x
According to the question,
Mass number of the element = 81
∴ (Number of protons number of neutrons) = 81
Hence, the number of protons in the element i.e., x is 35.
Since the atomic number of an atom is defined as the number of protons present in its nucleus, the atomic number of the given element is 35.
∴ The atomic symbol of the element is  .
.
Question 2.43: An ion with mass number 37 possesses one unit of negative charge. If the ion contains 11.1% more neutrons than the electrons, find the symbol of the ion.
Ans:- Let the number of electrons in the ion carrying a negative charge be x.
Then, Number of neutrons present = x + 11.1% of x
= x + 0.111 x
= 1.111 x
Number of electrons in the neutral atom = (x – 1)
(When an ion carries a negative charge, it carries an extra electron)
∴ Number of protons in the neutral atom = x – 1
Given, Mass number of the ion = 37
∴ (x – 1) + 1.111x = 37
2.111x = 38
x = 18
∴The symbol of the ion is 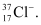
Question 2.44: An ion with mass number 56 contains 3 units of positive charge and 30.4% more neutrons than electrons. Assign the symbol to this ion.
Ans:- Let the number of electrons present in ion 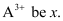
∴ Number of neutrons in it = x + 30.4% of x = 1.304 x
Since the ion is tri-positive,
⇒ Number of electrons in neutral atom = x + 3
∴ Number of protons in neutral atom = x + 3
Given, Mass number of the ion = 56
∴ Number of protons = x + 3 = 23 + 3 = 26
∴ The symbol of the ion 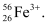
Question 2.45: Arrange the following type of radiations in increasing order of frequency:
(a) radiation from microwave oven
(b) amber light from traffic signal
(c) radiation from FM radio
(d) cosmic rays from outer space and
(e) X-rays.
Ans:- The increasing order of frequency is as follows:
Radiation from FM radio < amber light < radiation from microwave oven < X- rays < cosmic rays
The increasing order of wavelength is as follows:
Cosmic rays < X-rays < radiation from microwave ovens < amber light < radiation of FM radio
Question 2.46: Nitrogen laser produces a radiation at a wavelength of 337.1 nm. If the number of photons emitted is 5.6 × 1024, calculate the power of this laser.
Ans:- Power of laser = Energy with which it emits photons
Power 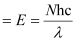
Where,
N = number of photons emitted
h = Planck’s constant
c = velocity of radiation
λ = wavelength of radiation
Substituting the values in the given expression of Energy (E):
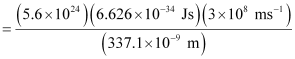
E = 0.3302 × 107 J
= 3.33 × 106 J
Hence, the power of the laser is 3.33 × 106 J.
Question 2.47: Neon gas is generally used in the sign boards. If it emits strongly at 616 nm, calculate
(a) the frequency of emission,
(b) distance traveled by this radiation in 30 s
(c) energy of quantum and
(d) number of quanta present if it produces 2 J of energy.
Ans:- Wavelength of radiation emitted = 616 nm
= 616 × 10–9 m (Given)
(a) Frequency of emission 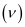

Where,
c = velocity of radiation
λ = wavelength of radiation
Substituting the values in the given expression of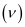 :
:
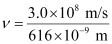
= 4.87 × 108 × 109 × 10–3 s–1
ν = 4.87 × 1014 s–1
Frequency of emission (ν) = 4.87 × 1014 s–1
(b) Velocity of radiation, (c) = 3.0 × 108 ms–1
Distance travelled by this radiation in 30 s
= (3.0 × 108 ms–1) (30 s)
= 9.0 × 109 m
(c) Energy of quantum (E) = hν
(6.626 × 10–34 Js) (4.87 × 1014 s–1)
Energy of quantum (E) = 32.27 × 10–20 J
(d) Energy of one photon (quantum) = 32.27 × 10–20 J
Therefore, 32.27 × 10–20 J of energy is present in 1 quantum.
Number of quanta in 2 J of energy
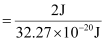
= 6.19 ×1018
= 6.2 ×1018
Question 2.48: In astronomical observations, signals observed from the distant stars are generally weak. If the photon detector receives a total of 3.15 × 10–18 J from the radiations of 600 nm, calculate the number of photons received by the detector.
Ans:- From the expression of energy of one photon (E),
E = hc / λ
Where,
λ = wavelength of radiation
h = Planck’s constant
c = velocity of radiation
Substituting the values in the given expression of E:
E 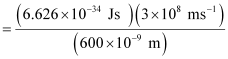
E = 3.313 × 10–19 J
Energy of one photon = 3.313 × 10–19 J
Number of photons received with 3.15 × 10–18 J energy

= 9.5 ≈ 10
Question 2.49: Lifetimes of the molecules in the excited states are often measured by using pulsed radiation source of duration nearly in the nano second range. If the radiation source has the duration of 2 ns and the number of photons emitted during the pulse source is 2.5 × 1015, calculate the energy of the source.
Ans:- Frequency of radiation (ν),
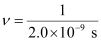
ν = 5.0 × 108 s–1
Energy (E) of source = Nhν
Where,
N = number of photons emitted
h = Planck’s constant
ν = frequency of radiation
Substituting the values in the given expression of (E):
E = (2.5 × 1015) (6.626 × 10–34 Js) (5.0 × 108 s–1)
E = 8.282 × 10–10 J
Hence, the energy of the source (E) is 8.282 × 10–10 J.
Question 2.50: The longest wavelength doublet absorption transition is observed at 589 and 589.6 nm. Calculate the frequency of each transition and energy difference between two excited states.
Ans:-
For λ1 = 589 nm
Frequency of transition
Frequency of transition (ν1) = c / λ1
= 5.093 × 1014 s–1
Similarly, for λ2 = 589.6 nm
Frequency of transition
Frequency of transition (ν2) = c / λ2
=5.088 × 1014 s–1
Energy difference (ΔE) between excited states = E1 – E2
Where,
E2 = energy associated with λ2
E1 = energy associated with λ1
ΔE = hν1 – hν2
= h(ν1 – ν2)
= (6.626 × 10–34 Js) (5.093 × 1014 – 5.088 × 1014)s–1
= (6.626 × 10–34 J) (5.0 × 10–3 × 1014)
ΔE = 3.31 × 10–22 J.

Question 2.51: The work function for caesium atom is 1.9 eV. Calculate
(a) the threshold wavelength and
(b) the threshold frequency of the radiation. If the caesium element is irradiated with a wavelength 500 nm, calculate the kinetic energy and the velocity of the ejected photoelectron.
Ans:- It is given that the work function (W0) for caesium atom is 1.9 eV.
(a) From the expression, , we get:
Where,
λ0 = threshold wavelength
h = Planck’s constant
c = velocity of radiation
Substituting the values in the given expression of (λ0):
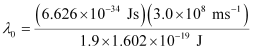
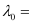 6.53 × 10–7 m
6.53 × 10–7 m
Hence, the threshold wavelength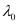 is 653 nm.
is 653 nm.
(b) From the expression,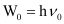 , we get:
, we get:
Vo = W0/h
Where, ν0 = threshold frequency
h = Planck’s constant
Substituting the values in the given expression of ν0:
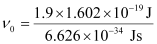
(1 eV = 1.602 × 10–19 J)
ν0 = 4.593 × 1014 s–1
Hence, the threshold frequency of radiation (ν0) is 4.593 × 1014 s–1.
(c) According to the question:
Wavelength used in irradiation (λ) = 500 nm
Kinetic energy = h (ν – ν0)
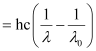
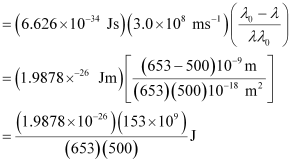
= 9.3149 × 10–20 J
Kinetic energy of the ejected photoelectron = 9.3149 × 10–20J
Since K.E 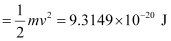

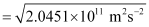 = 4.52 × 105 ms–1
= 4.52 × 105 ms–1
Hence, the velocity of the ejected photoelectron (v) is 4.52 × 105 ms–1.
Question 2.52: Following results are observed when sodium metal is irradiated with different wavelengths. Calculate (a) threshold wavelength and, (b) Planck’s constant.
Ans:- (a) Assuming the threshold wavelength to be
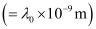 , the kinetic energy of the radiation is given as:
, the kinetic energy of the radiation is given as:
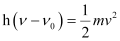
Three different equalities can be formed by the given value as:
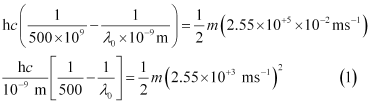
Similarly,
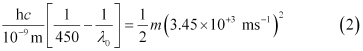
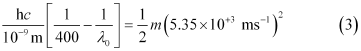
Dividing equation (3) by equation (1):
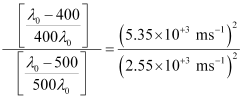
 Threshold wavelength
Threshold wavelength 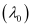 = 540 nm
= 540 nm
Note: part (b) of the question is not done due to the incorrect values of velocity given in the question.
Q. 2.53 The ejection of the photoelectron from the silver metal in the photoelectric effect experiment can be stopped by applying the voltage of 0.35 V when the radiation 256.7 nm is used. Calculate the work function for silver metal.
Ans. From the principle of conservation of energy, the energy of an incident photon (E) is equal to the sum of the work function (W0) of radiation and its kinetic energy (K.E) i.e.,
E = W0 K.E
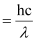 ⇒ W0 = E – K.E
⇒ W0 = E – K.E
Energy of incident photon (E)
Where,
c = velocity of radiation
h = Planck’s constant
λ = wavelength of radiation
Substituting the values in the given expression of E:
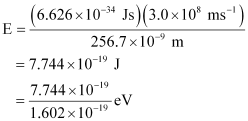
E = 4.83 eV
The potential applied to silver metal changes to kinetic energy (K.E) of the photoelectron. Hence,
K.E = 0.35 V
K.E= 0.35 eV
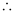 Work function, W0 = E – K.E
Work function, W0 = E – K.E
= 4.83 eV – 0.35 eV
= 4.48 eV
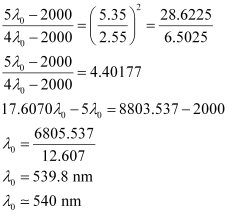
Q. 2.54 If the photon of the wavelength 150 pm strikes an atom and one of its inner bound electrons is ejected out with a velocity of 1.5 × 107 ms–1, calculate the energy with which it is bound to the nucleus.
Ans. Energy of incident photon (E) is given by,
E = hc / λ
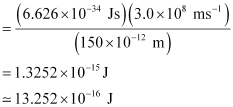
Energy of the electron ejected (K.E)

= 10.2480 × 10–17 J = 1.025 × 10–16J
Hence, the energy with which the electron is bound to the nucleus can be obtained as:
E – K.E = 13.252 × 10–16 J – 1.025 × 10–16 J
= 12.227 × 10–16 J

Q. 2.55 Emission transitions in the Paschen series end at orbit n = 3 and start from orbit n and can be represented as v = 3.29 × 1015 (Hz) [1/32 – 1/n2] . Calculate the value of n if the transition is observed at 1285 nm. Find the region of the spectrum.
Ans. Wavelength of transition = 1285 nm
= 1285 × 10–9 m (Given)
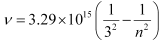 (Given)
(Given)
Since v = c/λ
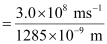
ν = 2.33 × 1014 s–1
Substituting the value of ν in the given expression,
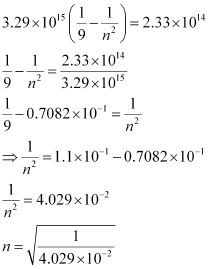
n = 4.98 ≈ 5
Hence, for the transition to be observed at 1285 nm, n = 5.
The spectrum lies in the infra-red region.
Q. 2.56 Calculate the wavelength for the emission transition if it starts from the orbit having radius 1.3225 nm & ends at 211.6 pm. Name the series to which this transition belongs & the region of the spectrum.
Ans. The radius of the nth orbit of hydrogen-like particles is given by,
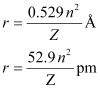
For radius (r1) = 1.3225 nm
= 1.32225 × 10–9 m
= 1322.25 × 10–12 m
= 1322.25 pm
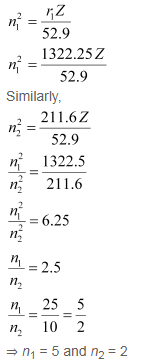
Thus, the transition is from the 5th orbit to the 2nd orbit. It belongs to the Balmer series.
Wave number 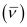 for the transition is given by,
for the transition is given by,
1.097 × 107 m–1 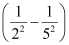
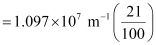
= 2.303 × 106 m–1
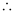 Wavelength (λ) associated with the emission transition is given by,
Wavelength (λ) associated with the emission transition is given by,
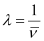
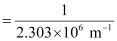
= 0.434 ×10–6 m
λ = 434 nm
Q. 2.57 Dual behaviour of matter proposed by de Broglie led to the discovery of electron microscope often used for the highly magnified images of biological molecules & other type of material. If the velocity of the electron in this microscope is 1.6×106 ms–1, calculate de Broglie wavelength associated with this electron.
Ans. From de Broglie’s equation,
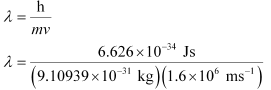
= 4.55 × 10–10 m = 455 pm
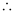 de Broglie’s wavelength associated with the electron is 455 pm.
de Broglie’s wavelength associated with the electron is 455 pm.
Q. 2.58 Similar to electron diffraction, neutron diffraction microscope is also used for the determination of the structure of molecules. If the wavelength used here is 800 pm, calculate the characteristic velocity associated with the neutron.
Ans. From de Broglie’s equation,
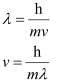
Where,
v = velocity of particle (neutron)
h = Planck’s constant
m = mass of particle (neutron)
λ = wavelength
Substituting the values in the expression of velocity (v),
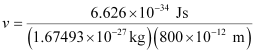
= 4.94 × 102 ms–1
v = 494 ms–1
 Velocity associated with the neutron = 494 ms–1
Velocity associated with the neutron = 494 ms–1
Q. 2.59 If the velocity of the electron in Bohr’s first orbit is 2.19 × 106 ms–1, calculate the de Broglie wavelength associated with it.
Ans. According to de Broglie’s equation,
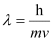
Where,
λ = wavelength associated with the electron
h = Planck’s constant
m = mass of electron
v = velocity of electron
Substituting the values in the expression of λ:
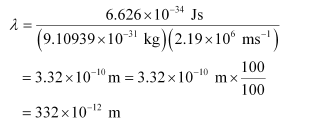
λ = 332 pm
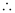 Wavelength associated with the electron = 332 pm
Wavelength associated with the electron = 332 pm
Q. 2.60 The velocity associated with a proton moving in a potential difference of 1000 V is 4.37 × 105 ms–1. If the hockey ball of mass 0.1 kg is moving with this velocity, calculate the wavelength associated with this velocity.
Ans. According to De Broglie’s expression,
λ = h/mv
Substituting the values in the expression,
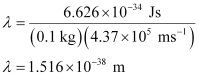
Q. 2.61 If the position of the electron is measured within an accuracy of 0.002 nm, calculate the uncertainty in the momentum of the electron. Suppose the momentum of the electron is h/4πm × 0.05 nm, is there any problem in defining this value.
Ans. From Heisenberg’s uncertainty principle,
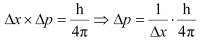
Where,
Δx = uncertainty in position of the electron
Δp = uncertainty in momentum of the electron
Substituting the values in the expression of Δp:
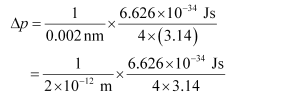
= 2.637 × 10–23 Jsm–1
Δp = 2.637 × 10–23 kgms–1 (1 J = 1 kgms2s–1)
 Uncertainty in the momentum of the electron = 2.637 × 10–23 kgms–1.
Uncertainty in the momentum of the electron = 2.637 × 10–23 kgms–1.
Actual momentum = 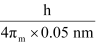
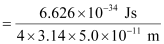
= 1.055 × 10–24 kgms–1
Since the magnitude of the actual momentum is smaller than the uncertainty, the value cannot be defined.
Q. 2.62 The quantum numbers of six electrons are given below. Arrange them in order of increasing energies. If any of these combination(s) has/have the same energy lists:
(1). n = 4, l = 2, ml = –2 , ms = –1/2
(2). n = 3, l = 2, ml= 1 , ms = 1/2
(3). n = 4, l = 1, ml = 0 , ms = 1/2
(4). n = 3, l = 2, ml = –2 , ms = –1/2
(5). n = 3, l = 1, ml = –1 , ms= 1/2
(6). n = 4, l = 1, ml = 0 , ms = 1/2
Ans. For n = 4 and l = 2, the orbital occupied is 4d.
For n = 3 and l = 2, the orbital occupied is 3d.
For n = 4 and l = 1, the orbital occupied is 4p.
Hence, the six electrons i.e., 1, 2, 3, 4, 5, and 6 are present in the 4d, 3d, 4p, 3d, 3p, and 4p orbitals respectively.
Therefore, the increasing order of energies is 5(3p) < 2(3d) = 4(3d) < 3(4p) = 6(4p) < 1 (4d).
Q. 2.63 The bromine atom possesses 35 electrons.It contains 6 electrons in 2p orbital,6 electrons in 3p orbital & 5 electrons in 4p orbital. Which of these electron experiences the lowest effective nuclear charge?
Ans. Nuclear charge experienced by an electron (present in a multi-electron atom) is dependant upon the distance between the nucleus and the orbital, in which the electron is present. As the distance increases, the effective nuclear charge also decreases.
Among p-orbitals, 4p orbitals are farthest from the nucleus of bromine atom with ( 35) charge. Hence, the electrons in the 4p orbital will experience the lowest effective nuclear charge. These electrons are shielded by electrons present in the 2p and 3p orbitals along with the s-orbitals. Therefore, they will experience the lowest nuclear charge.
Q. 2.64 Among the following pairs of orbitals which orbital will experience the larger effective nuclear charge?
(i) 2s and 3s,
(ii) 4d and 4f,
(iii) 3d and 3p
Ans. Nuclear charge is defined as the net positive charge experienced by an electron in the orbital of a multi-electron atom. The closer the orbital, the greater is the nuclear charge experienced by the electron (s) in it.
(i) The electron(s) present in the 2s orbital will experience greater nuclear charge (being closer to the nucleus) than the electron(s) in the 3s orbital.
(ii) 4d will experience greater nuclear charge than 4f since 4d is closer to the nucleus.
(iii) 3p will experience greater nuclear charge since it is closer to the nucleus than 3f.
Q. 2.65 The unpaired electrons in Al and Si are present in 3p orbital. Which electrons will experience more effective nuclear charge from the nucleus?
Ans. Nuclear charge is defined as the net positive charge experienced by an electron in a multi-electron atom.The higher the atomic number,the higher is the nuclear charge. Silicon has 14 protons while aluminium has 13 protons. Hence, silicon has a larger nuclear charge of ( 14) than aluminium, which has a nuclear charge of ( 13) Thus, the electrons in the 3p orbital of silicon will experience a more effective nuclear charge than aluminium.
Q. 2.66 Indicate the number of unpaired electrons in:
(a) P,
(b) Si,
(c) Cr,
(d) Fe
(e) Kr.
Ans. (a) Phosphorus (P):
Atomic number = 15
The electronic configuration of P is:
1s2 2s2 2p6 3s2 3p3
The orbital picture of P can be represented as:
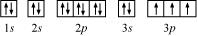
From the orbital picture, phosphorus has three unpaired electrons.
(b) Silicon (Si):
Atomic number = 14
The electronic configuration of Si is:
1s2 2s2 2p6 3s2 3p2
The orbital picture of Si can be represented as:
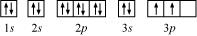
From the orbital picture, silicon has two unpaired electrons.
(c) Chromium (Cr):
Atomic number = 24
The electronic configuration of Cr is:
1s2 2s2 2p6 3s2 3p6 4s1 3d5
The orbital picture of chromium is:
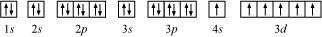
From the orbital picture, chromium has six unpaired electrons.
(d) Iron (Fe):
Atomic number = 26
The electronic configuration is:
1s2 2s2 2p6 3s2 3p6 4s2 3d6
The orbital picture of chromium is:
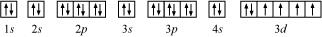
From the orbital picture, iron has four unpaired electrons.
(e) Krypton (Kr):
Atomic number = 36
The electronic configuration is:
1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6
The orbital picture of krypton is:
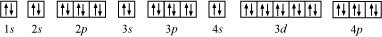
Since all orbitals are fully occupied, there are no unpaired electrons in krypton.
Q. 2.67
(a) How many sub-shells are associated with n = 4?
(b) How many electrons will be present in the sub-shells having ms value of –1/2 for n = 4?
Ans. (a) n = 4 (Given)
For a given value of ‘n’, ‘l’ can have values from zero to (n – 1).
∴ l = 0, 1, 2, 3
Thus, four sub-shells are associated with n = 4, which are s, p, d and f.
(b) Number of orbitals in the nth shell = n2
For n = 4
Number of orbitals = 16
If each orbital is taken fully, then it will have 1 electron with ms value of - ½.
∴ Number of electrons with ms value of (- ½ ) is 16.
FAQs on Structure of Atom - 2 NCERT Solutions - RRB Group D / RPF Constable
| 1. What is the structure of an atom? |  |
| 2. How are protons, neutrons, and electrons arranged in an atom? |  |
| 3. What is the significance of the atomic number and mass number of an atom? |  |
| 4. How do electrons occupy different energy levels in an atom? |  |
| 5. What is the role of electrons in chemical bonding? |  |




















