NCERT Solutions Class 12 Maths Chapter 11 - Three Dimensional Geometry
Three Dimensional Geometry
Question 1: If a line makes angles 90°, 135°, 45° with x, y and z-axes respectively, find its direction cosines.
ANSWER : - Let direction cosines of the line be l, m, and n.
Therefore, the direction Cosines of the line are
Question 2: Find the direction cosines of a line which makes equal angles with the coordinate axes.
ANSWER : - Let the direction cosines of the line make an angle α with each of the coordinate axes
Thus, direction cosines of the line make an angle α with each of the coordinate axes
Question 3: If a line has the direction ratios −18, 12, −4, then what are its direction cosines?
ANSWER : - If a line has direction ratios of −18, 12, and −4, then its direction cosines are
Thus, the direction cosines are -9/11, 6/11, -2/11
Question 4: Show that the points (2, 3, 4), (−1, −2, 1), (5, 8, 7) are collinear.
ANSWER : - The given points are A (2, 3, 4), B (− 1, − 2, 1), and C (5, 8, 7).
It is known that the direction ratios of line joining the points, (x1, y1, z1) and (x2, y2, z2), are given by, x2 − x1, y2 − y1, and z2 − z1.
The direction ratios of AB are (−1 − 2), (−2 − 3), and (1 − 4) i.e., −3, −5, and −3.
The direction ratios of BC are (5 − (− 1)), (8 − (− 2)), and (7 − 1) i.e., 6, 10, and 6.
It can be seen that the direction ratios of BC are −2 times that of AB i.e., they are proportional.
Therefore, AB is parallel to BC. Since point B is common to both AB and BC, points A, B, and C are collinear.
Question 5: Find the direction cosines of the sides of the triangle whose vertices are (3, 5, − 4), (− 1, 1, 2) and (− 5, − 5, − 2)
ANSWER : - The vertices of ΔABC are A (3, 5, −4), B (−1, 1, 2), and C (−5, −5, −2).
The direction ratios of side AB are (−1 − 3), (1 − 5), and (2 − (−4)) i.e., −4, −4, and 6.
Therefore, the direction cosines of AB are
Therefore, the direction cosines of BC are
Therefore, the direction cosines of AC are
Question 7: Show that the line through the points (1, −1, 2) (3, 4, −2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).
ANSWER : - Let AB be the line joining the points, (1, −1, 2) and (3, 4, − 2), and CD be the line joining the points, (0, 3, 2) and (3, 5, 6).
The direction ratios, a1, b1, c1, of AB are (3 − 1), (4 − (−1)), and (−2 − 2) i.e., 2, 5, and −4.
The direction ratios, a2, b2, c2, of CD are (3 − 0), (5 − 3), and (6 −2) i.e., 3, 2, and 4.
AB and CD will be perpendicular to each other, if a1a2 + b1b2 + c1c2 = 0
a1a2 b1b2 c1c2 = 2 × 3 5 × 2 (− 4) × 4
= 6 + 10 – 16 = 0
Therefore, AB and CD are perpendicular to each other.
Question 8: Show that the line through the points (4, 7, 8) (2, 3, 4) is parallel to the line through the points (−1, −2, 1), (1, 2, 5).
ANSWER : - Let AB be the line through the points, (4, 7, 8) and (2, 3, 4), and CD be the line through the points, (−1, −2, 1) and (1, 2, 5).
The directions ratios, a1, b1, c1, of AB are (2 − 4), (3 − 7), and (4 − 8) i.e., −2, −4, and −4.
The direction ratios, a2, b2, c2, of CD are (1 − (−1)), (2 − (−2)), and (5 − 1) i.e., 2, 4, and 4.
Thus, AB is parallel to CD.
Question 9: Find the equation of the line which passes through the point (1, 2, 3) and is parallel to the vector .
ANSWER : - It is given that the line passes through the point A (1, 2, 3). Therefore, the position vector through A is
It is known that the line which passes through point A and parallel to is given by is a constant
Question 10: Find the equation of the line in vector and in Cartesian form that passes through the point with position vector 2i - j +4k and is in the direction i + 2j - k .
ANSWER : - It is given that the line passes through the point with position vector
It is known that, a line through a point with position vector is given by the equations
Eliminating λ, we obtain the Cartesian form equation as
Question 11: Find the Cartesian equation of the line which passes through the point (−2, 4, −5) and parallel to the line given by
Answer: It is given that the line passes through the point (−2, 4, −5) and is parallel to
The direction ratios of the line are 3, 5, and 6.
The required line is parallel to
Therefore, its direction ratios are 3k, 5k, and 6k, where k ≠ 0
It is known that the equation of the line through the point (x1, y1, z1) and with direction ratios, a, b, c, is given by
Therefore the equation of the required line is
Question 12: The Cartesian equation of a line is Write its vector form.
ANSWER : - The Cartesian equation of the line is
...(1)
The given line passes through the point (5, −4, 6). The position vector of this point is
Also, the direction ratios of the given line are 3, 7, and 2.
This means that the line is in the direction of vector,
It is known that the line through position vector and in the direction of the vector is given by the equation
This is the required equation of the given line in vector form
Question 13: Find the vector and the Cartesian equations of the lines that pass through the origin and (5, −2, 3).
ANSWER : -
The required line passes through the origin. Therefore, its position vector is given by, a = 0 ..(1)
The direction ratios of the line through origin and (5, −2, 3) are
(5 − 0) = 5, (−2 − 0) = −2, (3 − 0) = 3
The line is parallel to the vector given by the equation
The equation of the line in vector form through a point with position vector a and parallel to b is,
The equation of the line through the point (x1, y1, z1) and direction ratios a, b, c is given by,
Therefore, the equation of the required line in the Cartesian form is
Question 14: Find the vector and the Cartesian equations of the line that passes through the points (3, −2, −5), (3, −2, 6).
ANSWER : - Let the line passing through the points, P (3, −2, −5) and Q (3, −2, 6), be PQ.
Since PQ passes through P (3, −2, −5), its position vector is given by,
The direction ratios of PQ are given by,
(3 − 3) = 0, (−2 2) = 0, (6 5) = 11
The equation of the vector in the direction of PQ is
The equation of PQ in Cartesian form is
Question 15: Find the angle between the following pairs of lines:
and
ANSWER : - (i) Let Q be the angle between the given lines.
The angle between the given pairs of lines is given by,
(ii) The given lines are parallel to the vectors ,respectively.
Question 16: Find the angle between the following pairs of lines:
1.
2.
ANSWER : - Let and be the vectors parallel to the pair of lines respectively.
The angle, Q, between the given pair of lines is given by the relation
(ii) Let be the vectors parallel to the given pair of lines, respectively.
Question 17: Find the values of p so the line are at right angles
Answer: The given equations can be written in the standard form as
The direction ratios of the lines are −3,2p/7,2,-3p/7,1,-5, respectively.
Two lines with direction ratios, a1, b1, c1 and a2, b2, c2, are perpendicular to each other, if a1a2 + b1 b2 + c1c2 = 0
Question 18: Show that the lines are perpendicular to each other.
ANSWER : - The equations of the given lines are
The direction ratios of the given lines are 7, −5, 1 and 1, 2, 3 respectively.
Two lines with direction ratios, a1, b1, c1 and a2, b2, c2, are perpendicular to each other
if a1a2 + b1 b2 + c1c2 = 0
∴ 7 × 1 + (−5) × 2 + 1 × 3
= 7 − 10 + 3
= 0
Therefore, the given lines are perpendicular to each other.
Question 19: Find the shortest distance between the lines
ANSWER : - The equations of the given lines are
It is known that the shortest distance between the lines
..(1)
Comparing the given equations, we obtain
Substituting all the values in equation (1), we obtain
Therefore, the shortest distance between the two lines is 3√2/2 units
Question 20: Find the shortest distance between the lines
ANSWER : - The given lines are
It is known that the shortest distance between the two
lines, , is given by.
.....(1)
Comparing the given equations, we obtain
Substituting all the values in equation (1), we obtain
Since distance is always non-negative, the distance between the given lines is units.
Question 21: Find the shortest distance between the lines whose vector equations are
ANSWER : - The given lines are and
It is known that the shortest distance between the lines. , is given by.
...(i)
Comparing the given equations with
obtain
Substituting all the values in equation (1).. we obtain
Therefore, the shortest distance between the two given lines is units.
ANSWER:-The given lilies are
It is known that the shortest distance between the lines, is given by.
For the given equations,
Substituting all the values in equation (3).. we obtain
Therefore, the shortest, distance between the lines is units.
Question 23: In each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin.
(a) z = 2
(b) x + y + z = I
(c) 2x+3y-z = 5
(d) 5y+ 8 = 0
ANSWER : - (a) The equation of the plane is z = 2 or 0x + 0y + z = 2 … (1)
The direction ratios of normal are 0, 0, and 1.
This is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of the perpendicular drawn from the origin.
Therefore, the direction cosines are 0, 0, and 1 and the distance of the plane from the origin is 2 units.
(b) x + y + z = 1 … (1)
The direction ratios of normal are 1, 1, and 1.
Dividing both sides of equation (1) by √3, , we obtain
This equation is of the form are the direction cosines of normal to the plane andd is the distance of normal from the origin.
Therefore, the direction cosines of the normal are and the distance of normal from the origin is
(c) 2x+3y - z = 5 ... (1)
The direction ratios of normal are 2. 3. and-1.
Dividing both sides of equation (1) by, we obtain
This equation is of the form are the direction cosines of normal to the plane and d is the distance of normal from the origin.
Therefore, the direction cosines of the normal to the plane are and the distance of normal from the origin is
units.
(d) 5y + 8 = 0
⇒ 0x- 5y + 0z = 8 ... (1)
The direction ratios of normal are 0,-5, and 0.
Dividing both sides of equation (1) by 5, we obtain
This equation is of the form lx + my + nz = d. where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.
Therefore, the direction cosines of the normal to the plane are 0, -1, and 0 and the distance of normal
Question 24: Find the vector equation of a plane which is at a distance of 7 units from the origin and normal to the vector
ANSWER : - The normal vector is
It is known that the equation of the plane with position vector
This is the vector equation of the required plane.
Question 25: Find the Cartesian equation of the following planes:
ANSWER:-(a) It is given that equation of the plane is
For any arbitrary point P (x.. y. z) on the plane, position vector
Substituting the value of in equation (1), we obtain
This is the Cartesian equation of the plane.
For any arbitrary point P (x, y. z) on the plane, position vector
Substituting the value of equation (1), we obtain
This is the Cartesian equation of the plane.
For any arbitrary point P (x,y, z) on the plane, position vector
Substituting the value of equation (1), we obtain
This is the Cartesian equation of the given plane.
Question 26: In the following cases, find the coordinates of the foot of the perpendicular drawn from the origin.
(a) 2x + 3y + 4z -12 = 0
(b) 3y + 4z - 6 = 0
(c) x + y+z = 1
(d) 5 v + 8 = 0
ANSWER: - (a) Let the coordinates of the foot of perpendicular P from the origin to the plane be
(x1,y1,z1)
2x + 3 y + 4 z - 12=0
⇒ 2x + 3y + 4z = 12 ... (1)
The direction ratios of normal are 2, 3, and 4.
Dividing both sides of equation (1) by , we obtain
This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin
The coordinates of the foot of the perpendicular are given by (Id. md. nd).
Therefore, the coordinates of the foot of the perpendicular are
(b) Let the coordinates of the foot of perpendicular P from the origin to the plane be (x1, y1 z1)
3y + 4z - 6 = 0
The direction ratios of the normal are 0; 3. and 4.
Dividing both sides of equation (1) by 5, we obtain
This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.
The coordinates of the foot of the perpendicular are given by
(ld, md, nd).
Therefore, the coordinates of the foot of the perpendicular are
(c) Let the coordinates of the foot of perpendicular P from the origin to the plane be (x1,y1,z1)
x+y + z = 1 ... (1)
The direction ratios of the normal are 1, 1, and 1.
Dividing both sides of equation (1) by √3, , we obtain
This equation is of the form lx + my + nz = d. where l, m. n are the direction cosines of normal to the plane andd is the distance of normal from the origin.
The coordinates of the foot of the perpendicular are given by (Id. md. nd).
Therefore, the coordinates of the foot of the nemendicular are
(d) Let the coordinates of the foot of perpendicular P from the origin to the plane be (x1,y1,z1).
5y + 8 = 0
⇒ 0x- 5y + 0z = 8 ... (1)
The direction ratios of the normal are 0, −5, and 0.
Dividing both sides of equation (1) by 5, we obtain
This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.
The coordinates of the foot of the perpendicular are given by
(ld, md, nd).
Therefore, the coordinates of the foot of the perpendicular are (0,-1,0) and (0,-8/5, 0)
Question 27: Find the vector and Cartesian equation of the planes
(a) that passes through the point (1, 0, −2) and the normal to the plane .
(b) that passes through the point (1, 4, 6) and the normal vector to the plane
ANSWER : - (a) The position vector of point (1, 0,-2) is
The normal vector perpendicular to the plane is
The vector equation of the plane is given by,
is the position vector of any point P (x, y. z) in the plane.
Therefore, equation (1) becomes
This is the Cartesian equation of the required plane.
(b) The position vector of the point (1. 4, 6) is
The normal vector perpendicular to the plane is
The vector equation of the plane is given by.
is the position vector of any point P (x,y\ z) in the plane
Therefore, equation (1) becomes
This is the Cartesian equation of the required plane.
Question 28: Find the equations of the planes that passes through three points.
(a) (1, 1,-1), (6,4, -5), (-4, -2, 3)
(b) (1,1,0), (1,2, 1), (-2,2,-1)
ANSWER: - (a) The given points are A (1,1, - 1),B (6. 4, -5), and C (-4. - 2, 3).
= 2+2-4
= 0
Since A,B,C are collinear points.there will be infinite number of planes passing through the given points.
(b) The given points are A (1,1,0),B (1,2, 1), andC (-2,2,-1).
It is known that the equation of the plane through the points.
This is the Cartesian equation of the required plane.
Question 29: Find the intercepts cut off by the plane 2x + y -z = 5
ANSWER:- 2x + y - z = 5 ..... (1)
Dividing both sides of equation (1) by 5, we obtain
It is known that the equation of a plane in intercept form is , where a, b, c are the intercepts cut off by the plane at x,y, and z axes respectively.
Therefore, for the given equation.
Thus, the intercepts cut off by the plane are
Question 30: Find the equation of the plane with intercept 3 on the y-axis and parallel to ZOX plane.
ANSWER : - The equation of the plane ZOX is
y = 0
Any plane parallel to it is of the form, y = a
Since the y-intercept of the plane is 3,
∴ a = 3
Thus, the equation of the required plane is y = 3
Question 31: Find the equation of the plane through the intersection of the planes point (2, 2, 1)
ANSWER : - The equation of any plane through the intersection of the planes,
3x − y + 2z − 4 = 0 and x + y + z − 2 = 0, is
.......(1)
The plane passes through the point (2, 2, 1). Therefore, this point will satisfy equation (1).
Substituting ill equation (1). we obtain
This is the required equation of the plane.
Question 32: Find the vector equation of the plane passing through the intersection of the planes and through the point (2.1, 3)
ANSWER : - The equations of the planes are
The equation of any plane through the intersection of the planes given in equations (1) and (2) is given by;
Hie plane passes through the point ('2,1,3). Therefore. its position vector is given by,
Substituting ill equation (3). we obtain
Substituting in equation (3), we obtain
This is the vector equation of the required plane.
Question 33: Find the equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y+ 4z = 5 which is perpendicular to the plane x - y + z = 1
ANSWER : - The equation of the plane through the intersection of the planes, x + y + z = 1 and 2x + 3y + 4z = 5, is
The direction ratios, a1,b1,c1, of this plane are (2λ + 1). (3λ+ 1), and (4λ+ 1).
The plane in equation (1) is perpendicular to x- y + z = 0
Its direction ratios, a2,b2,c2, are 1,-1, and 1.
Since the planes are perpendicular,
Substituting in equation (1), we obtain
This is the required equation of the plane.
Question 34: Find the angle between the planes whose vector equations are and
ANSWER : - The equations of the given planes are
It is known that if are normal to the planes.
, then the angle between them. Q. is given by.
Substituting the value of ill equation (1), we obtain
Question 35: In the following cases, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.
Therefore, the given planes are not parallel.
The angle between them is given by,
ANSWER : - The direction ratios of normal to the plane. and
The angle between L1 and L2 is given by,
(a) The equations of the planes are 7x - 5y - 6z- 30=0 and
Therefore, the given planes are not perpendicular.
Therefore, the given planes are not parallel.
The angle between them is given by,
(b) The equations of the planes are
Thus, the given planes are perpendicular to each other.
(c) The equations of the given planes are
Thus, the given planes are not perpendicular to each other.
Thus, the given planes are parallel to each other.
(d) The equations of the planes are
Thus, the given lines are parallel to each other
(e) The equations of the given planes are
Therefore, the given lines are not perpendicular to each other.
Therefore, the given lines are not parallel to each other.
The angle between the planes is given by,
Question 36: In the following cases, find the distance of each of the given points from the corresponding given plane.
Point Plane
(a) (0, 0, 0) 3x - 4y +12 = 3
(b) (3, -2,1) 2x-y + 2z + 3 = 0
(c)(2,3,-5) x+2y-2z = 9
(d)(-6,0,0) 2x-3y + bz-2 = 0
ANSWER : - It is known that the distance between a point, p(x1, y1, z1), and a plane, Ax+By+Cz = D, is given by,
(a) The given point is (0: 0. 0) and the plane is
(b) The given point is (3, - 2,1) and the plane is
(c) The given point is (2, 3,-5) and the plane is
(d) The given point is (—6,0. 0) and the plane is
Question 37: Show that the line joining the origin to the point (2, 1, 1) is perpendicular to the line determined by the points (3, 5, −1), (4, 3, −1).
ANSWER : - Let OA be the line joining the origin, O (0, 0, 0), and the point, A (2, 1, 1).
Also, let BC be the line joining the points, B (3, 5, −1) and C (4, 3, −1).
The direction ratios of OA are 2, 1, and 1 and of BC are (4 − 3) = 1, (3 − 5) = −2, and (−1 1) = 0
OA is perpendicular to BC, if a1a2 + b1b2 + c1c2 = 0
∴ a1a2 + b1b2 + c1c2 = 2 × 1 +1 (−2) + 1 ×0 = 2 − 2 = 0
Thus, OA is perpendicular to BC.
Question 38:If l1, m1, n1 and l2, m2, n2 are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these are m1n2 − m2n1,n1l2 − n2l1, l1m2 − l2m1.
ANSWER : - It is given that l1, m1, n1 and l2, m2, n2 are the direction cosines of two mutually perpendicular lines. Therefore,
Let l, m, n be the direction cosines of the line which is perpendicular to the line with direction cosines
l, m, n are the direction cosines of the line.
It is known that
From (1), (2).and(3), we obtain
Substituting the values from equations (5) and (6) in equation (4), we obtain
Thus, the direction cosines of the required line are
Question 39: Find the angle between the lines whose direction ratios are a. b. c and b - c. c - a. a - b.
ANSWER:-The angle O between the lines with direction cosines, a. b. c and b - c, c - a,
a - b. is given by.
Thus, the angle between the lines is 90°.
Question 40: Find the equation of a line parallel to x-axis and passing through the origin.
ANSWER : - The line parallel to x-axis and passing through the origin is x-axis itself.
Let A be a point on x-axis. Therefore, the coordinates of A are given by (a, 0, 0), where a ∈ R.
Direction ratios of OA are (a − 0) = a, 0, 0
The equation of OA is given by,
Thus, the equation of line parallel to x-axis and pas sing through origin is
Question 41: If the coordinates of the points A, B, C, D be (1, 2, 3), (4, 5, 7), (−4, 3, −6) and (2, 9, 2) respectively, then find the angle between the lines AB and CD.
ANSWER : - The coordinates of A, B, C, and D are (1, 2, 3), (4, 5, 7), (−4, 3, −6), and
(2, 9, 2) respectively.
The direction ratios of AB are (4 − 1) = 3, (5 − 2) = 3, and (7 − 3) = 4
The direction ratios of CD are (2 −(− 4)) = 6, (9 − 3) = 6, and (2 −(−6)) = 8
It can be seen that,
Therefore, AB is parallel to CD.
Thus, the angle between AB and CD is either 0° or 180°.
Question 42: If the lilies are petpendicular.find the value of k.
ANSWER : - The direction of ratios of the lines. , are -3, 2k, 2 and 3k,1, - 5 respectively.
It is known that two lines with direction ratios a1, b1, c1 and a2, b2, c2 are perpendicular,
if a1a2 + b1b2 + c1c2 = 0
Therefore, for . the given lines are perpendicular to each other.
Question 43: Find the vector equation of the plane passing through (1,2, 3) and perpendicular to the plane
ANSWER : - The position vector of the point (1, 2, 3) is
The direction ratios of the normal to the plane. .are 1.2. and -5 and the normal vector is
The equation of a line passing through a point and perpendicular to the given plane is given by,
Question 44: Find the equation of the plane passing through (a, b. c) and parallel to the plane
ANSWER : - Any plane parallel to the plane. , is of the form
The plane passes through the point (a. b. c). Therefore, the position vector of this point is
Therefore, equation (1) becomes
Substituting in equation (1), we obtain
Substituting in equation (2), we obtain
Question 45: Find the shortest distance between lines and
ANSWER: - The given lines are
It is known that the shortest distance betw een two lines. is given by
Comparing to equations (1) and (2), we obtain
Substituting all the values in equation (1), we obtain
Therefore, the shortest distance between the two given lines is 9 units.
Question 46: Find the coordinates of the point where the line through (5, 1, 6) and (3, 4, 1) crosses the YZ-plane
ANSWER: It is known that the equation of the line passing through the points, is
The line pas sing through the points. (5. 1. 6) and (3. 4. 1), is given by.
Any point, on the line is of the form (5 - 2k. 3k + 1, 6 - 5k).
The equation of YZ-plane is x = 0
Since the line passes through YZ-plane.
Therefore, the required point is
Question 47: Find the coordinates of the point where the line through (5,1, 6) and (3,4,1) crosses the ZX - plane.
ANSWER: - It is known that the equation of the line passing through the points, is
The line passing through the points, (5,1,6) and (3, 4,1), is given by,
Any point, on the line is of the form
Since the line passes through ZX-plane.
Therefore, the required point is
Question 48: Find the coordinates of the point where the line through (3, −4, −5) and (2, − 3, 1) crosses the plane 2x + y + z = 7).
ANSWER : - It is known that the equation of the line through the points, (x1, y1, z1) and (x2, y2, z2), is
Since the line passes through the points. its equation is given by.
Therefore, any point on the line is of the form
This point lies on the plane, 2x + y + z = 7
Hence, the coordinates of the required point are (3 − 2, 2 − 4, 6 × 2 − 5) i.e., (1, −2, 7).
Question 49: Find the equation of the plane passing through the point (−1, 3, 2) and perpendicular to each of the planes x + 2y + 3z = 5 and 3x + 3y + z = 0.
ANSWER : - The equation of the plane passing through the point (−1, 3, 2) is
a (x + 1) b (y − 3) c (z − 2) = 0 … (1)
where, a, b, c are the direction ratios of normal to the plane.
It is known that two planes  and
and 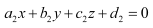 are perpendicular,
are perpendicular,
if 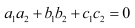
Plane (1) is perpendicular to the plane, x + 2y + 3z = 5

Also, plane (1) is perpendicular to the plane, 3x + 3y + z = 0

From equations (2) and (3), we obtain
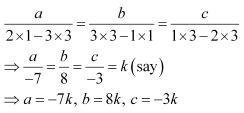
Substituting the values of a, b, and c in equation (1), we obtain
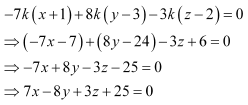
This is the required equation of the plane.
Question 51: Find the equation of the plane passing through the line of intersection of the planes and
and parallel to x-axis.
ANSWER : - The given planes are
The required plane is parallel to x-axis. Therefore, its normal is perpendicular to x-axis.
The direction ratios of x-axis are 1, 0, and 0
Therefore, its Cartesian equation is y − 3z + 6 = 0
This is the equation of the required plane.
Question 52: If O be the origin and the coordinates of P be (1, 2, −3), then find the equation of the plane passing through P and perpendicular to OP.
ANSWER : - The coordinates of the points, O and P, are (0, 0, 0) and (1, 2, −3) respectively.
Therefore, the direction ratios of OP are (1 − 0) = 1, (2 − 0) = 2, and (−3 − 0) = −3
It is known that the equation of the plane passing through the point (x1, y1 z1) is
where, a, b, and c are the direction ratios of normal.
Here, the direction ratios of normal are 1, 2, and −3 and the point P is (1, 2, −3).
Thus, the equation of the required plane is
Question 53: Find the equation of the plane which contains the line of intersection of the planes & which is perpendicular to the plane
ANSWER : - The equations of the given planes are
The equation of the plane passing through the line intersection of the plane given in equation (1) and equation (2) is
..(3)
The plane in equation (3) is perpendicular to the plane
Substituting l = 7/19in equation (3), we obtain
This is the vector equation of the required plane.
The Cartesian equation of this plane can be obtained by substituting in equation (3).
Question 54: Find the distance of the point (−1, −5, −10) from the point of intersection of the line and the plane
ANSWER : - The equation of the given line is
..(1)
The equation of the given plane is
..(2)
Substituting the value of r_ from equation (1) in equation (2), we obtain
Substituting this value in equation (1), we obtain the equation of the line as This means that the position vector of the point of intersection of the line & the plane is
This shows that the point of intersection of the given line and plane is given by the coordinates, (2, −1, 2). The point is (−1, −5, −10).
The distance d between the points, (2, −1, 2) and (−1, −5, −10), is
Question 55: Find the vector equation of the line passing through (1, 2, 3) and parallel to the planes
ANSWER : - Let the required line be parallel to vector b given by
The position vector of the point (1, 2, 3) is
The equation of line passing through (1, 2, 3) and parallel to b is given by,
The equations of the given planes are
The line in equation (1) and plane in equation (2) are parallel. Therefore, the normal to the plane of equation (2) and the given line are perpendicular.
From equations (4) and (5), we obtain
Therefore, the direction ratios of
Substituting the value of ill equation (1), we obtain
This is the equation of the required line.
Question 56: Find the vector equation of the line passing through the point (1, 2, − 4) and perpendicular to the two lines:
Answer: - Let the required line be parallel to the vector b given by,
The position vector of the point (1, 2, − 4) is
The equation of the line passing through (1, 2, −4) and parallel to vector b is
The equations of the lines are
Line (1) and line (2) are perpendicular to each other.
Also, line (1) and line (3 ) are perpendicular to each othei
From equations (4) and (5); we obtain
∴ Direction ratios of
Substituting ill equation (1), we obtain
This is the equation of the required line.
Question 57: Prove that if a plane has the intercepts a, b, c and is at a distance of P units from the origin, then
ANSWER : - The equation of a plane having intercepts a, b, c with x, y, and z axes respectively is given by,
The distance (p) of the plane from the origin is given by,
Question 58:Distance between the two planes: 2x +3y + 4z = 4 and 4x+6y+8z =12 is
(A)2 units
(B)4 units
(C)8 units
Answer:
The equations of the planes are
It can be seen that the given planes are parallel
It is known that the distance between two parallel planes, ax + by + cz = d1 and ax + by + cz = d2, is given by,
Thus, the distance between the lines is units
Hence, the correct answer is D.
Question 59: The planes: 2x − y + 4z = 5 and 5x − 2.5y + 10z = 6 are
(A) Perpendicular
(B) Parallel
(C) intersect y-axis
(C) passes through (0,0,5/4)
ANSWER : - The equations of the planes are
2x - y - 4z = 5 ... (1)
5x - 2.5y+ 10z = 6 ... (2)
It can be seen that.
Therefore, the given planes are parallel.
Hence, the correct answer is B.
Question 60: Name the octants in which the following points lie:
(1, 2, 3), (4, –2, 3), (4, –2, –5), (4, 2, –5), (–4, 2, –5), (–4, 2, 5), (–3, –1, 6), (2, –4, –7)
Answer
The x-coordinate, y-coordinate, and z-coordinate of point (1, 2, 3) are all positive. Therefore, this point lies in octant I.
The x-coordinate, y-coordinate, and z-coordinate of point (4, –2, 3) are positive, negative, and positive respectively. Therefore, this point lies in octant IV.
The x-coordinate, y-coordinate, and z-coordinate of point (4, –2, –5) are positive, negative, and negative respectively. Therefore, this point lies in octant VIII.
The x-coordinate, y-coordinate, and z-coordinate of point (4, 2, –5) are positive, positive, and negative respectively. Therefore, this point lies in octant V.
The x-coordinate, y-coordinate, and z-coordinate of point (–4, 2, –5) are negative, positive, and negative respectively. Therefore, this point lies in octant VI.
The x-coordinate, y-coordinate, and z-coordinate of point (–4, 2, 5) are negative, positive, and positive respectively. Therefore, this point lies in octant II.
The x-coordinate, y-coordinate, and z-coordinate of point (–3, –1, 6) are negative, negative, and positive respectively. Therefore, this point lies in octant III.
The x-coordinate, y-coordinate, and z-coordinate of point (2, –4, –7) are positive, negative, and negative respectively. Therefore, this point lies in octant VIII.
Question 61: Find the distance between the following pairs of points:
(i) (2, 3, 5) and (4, 3, 1) (ii) (–3, 7, 2) and (2, 4, –1)
(iii) (–1, 3, –4) and (1, –3, 4) (iv) (2, –1, 3) and (–2, 1, 3)
Answer
The distance between points P(x1, y1, z1) and P(x2, y2, z2) is given by 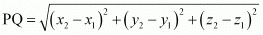
(i) Distance between points (2, 3, 5) and (4, 3, 1)
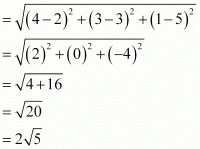
(ii) Distance between points (–3, 7, 2) and (2, 4, –1)
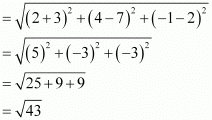
Question 62: Show that the points (–2, 3, 5), (1, 2, 3) and (7, 0, –1) are collinear.
Answer
Let points (–2, 3, 5), (1, 2, 3), and (7, 0, –1) be denoted by P, Q, and R respectively.
Points P, Q, and R are collinear if they lie on a line.
Here, PQ + QR 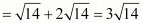 = PR
= PR
Hence, points P(–2, 3, 5), Q(1, 2, 3), and R(7, 0, –1) are collinear.
Question 63: Verify the following:
(i) (0, 7, –10), (1, 6, –6) and (4, 9, –6) are the vertices of an isosceles triangle.
(ii) (0, 7, 10), (–1, 6, 6) and (–4, 9, 6) are the vertices of a right angled triangle.
(iii) (–1, 2, 1), (1, –2, 5), (4, –7, 8) and (2, –3, 4) are the vertices of a parallelogram.
Answer
(i) Let points (0, 7, –10), (1, 6, –6), and (4, 9, –6) be denoted by A, B, and C respectively.
Here, AB = BC ≠ CA
Thus, the given points are the vertices of an isosceles triangle.
(ii) Let (0, 7, 10), (–1, 6, 6), and (–4, 9, 6) be denoted by A, B, and C respectively.
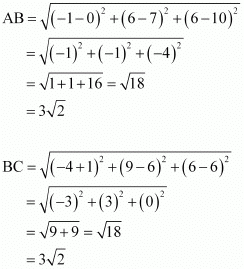
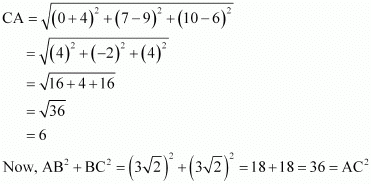
Therefore, by Pythagoras theorem, ABC is a right triangle.
Hence, the given points are the vertices of a right-angled triangle.
(iii) Let (–1, 2, 1), (1, –2, 5), (4, –7, 8), and (2, –3, 4) be denoted by A, B, C, and D respectively.
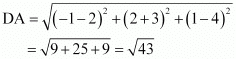
Here, AB = CD = 6, BC = AD =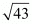
Hence, the opposite sides of quadrilateral ABCD, whose vertices are taken in order, are equal.
Therefore, ABCD is a parallelogram.
Hence, the given points are the vertices of a parallelogram.
Question 64: Find the equation of the set of points which are equidistant from the points (1, 2, 3) and (3, 2, –1).
Answer
Let P (x, y, z) be the point that is equidistant from points A(1, 2, 3) and B(3, 2, –1).
Accordingly, PA = PB
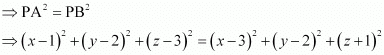
⇒ x2 – 2x + 1 + y2 – 4y + 4 + z2 – 6z + 9 = x2 – 6x + 9 + y2 – 4y + 4 + z2 + 2z + 1
⇒ –2x –4y – 6z + 14 = –6x – 4y + 2z + 14
⇒ – 2x – 6z + 6x – 2z = 0
⇒ 4x – 8z = 0
⇒ x – 2z = 0
Thus, the required equation is x – 2z = 0.
Question 65: Find the equation of the set of points P, the sum of whose distances from A (4, 0, 0) and B (–4, 0, 0) is equal to 10.
Answer
Let the coordinates of P be (x, y, z).
The coordinates of points A and B are (4, 0, 0) and (–4, 0, 0) respectively.
It is given that PA + PB = 10.
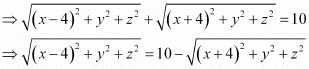
On squaring both sides, we obtain
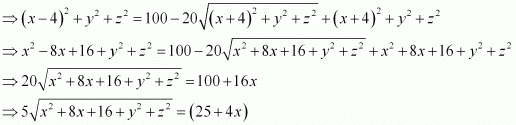
On squaring both sides again, we obtain
25 (x2 + 8x + 16 + y2 + z2) = 625 + 16x2 + 200x
⇒ 25x2 + 200x + 400 + 25y2 + 25z2 = 625 + 16x2 + 200x
⇒ 9x2 + 25y2 + 25z2 – 225 = 0
Thus, the required equation is 9x2 + 25y2 + 25z2 – 225 = 0.
Question 66:
Find the coordinates of the point which divides the line segment joining the points (–2, 3, 5) and (1, –4, 6) in the ratio (i) 2:3 internally, (ii) 2:3 externally.
Answer
(i) The coordinates of point R that divides the line segment joining points P (x1, y1, z1) and Q (x2, y2, z2) internally in the ratio m: n are
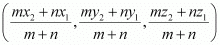 .
.
Let R (x, y, z) be the point that divides the line segment joining points(–2, 3, 5) and (1, –4, 6) internally in the ratio 2:3
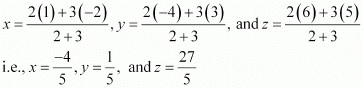
Thus, the coordinates of the required point are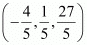 .
.
(ii) The coordinates of point R that divides the line segment joining points P (x1, y1, z1) and Q (x2, y2, z2) externally in the ratio m: n are
 .
.
Let R (x, y, z) be the point that divides the line segment joining points(–2, 3, 5) and (1, –4, 6) externally in the ratio 2:3
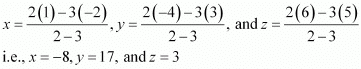
Thus, the coordinates of the required point are (–8, 17, 3).
Question 67:
Given that P (3, 2, –4), Q (5, 4, –6) and R (9, 8, –10) are collinear. Find the ratio in which Q divides PR.
Answer
Let point Q (5, 4, –6) divide the line segment joining points P (3, 2, –4) and R (9, 8, –10) in the ratio k:1.
Therefore, by section formula,
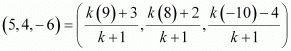
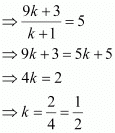
Thus, point Q divides PR in the ratio 1:2.
Question 68:
Find the ratio in which the YZ-plane divides the line segment formed by joining the points (–2, 4, 7) and (3, –5, 8).
Answer
Let the YZ planedivide the line segment joining points (–2, 4, 7) and (3, –5, 8) in the ratio k:1.
Hence, by section formula, the coordinates of point of intersection are given by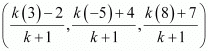
On the YZ plane, the x-coordinate of any point is zero.
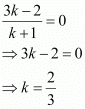
Thus, the YZ plane divides the line segment formed by joining the given points in the ratio 2:3.
Question 67:
Using section formula, show that the points A (2, –3, 4), B (–1, 2, 1) and 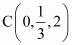 are collinear.
are collinear.
Answer
The given points are A (2, –3, 4), B (–1, 2, 1), and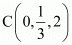 .
.
Let P be a point that divides AB in the ratio k:1.
Hence, by section formula, the coordinates of P are given by
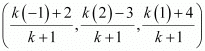
Now, we find the value of k at which point P coincides with point C.
By taking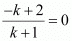 , we obtain k = 2.
, we obtain k = 2.
For k = 2, the coordinates of point P are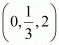 .
.
i.e., 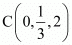 is a point that divides AB externally in the ratio 2:1 and is the same as point P.
is a point that divides AB externally in the ratio 2:1 and is the same as point P.
Hence, points A, B, and C are collinear.
Question 68:
Find the coordinates of the points which trisect the line segment joining the points P (4, 2, –6) and Q (10, –16, 6).
Answer
Let A and B be the points that trisect the line segment joining points P (4, 2, –6) and Q (10, –16, 6)
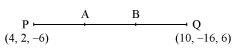
Point A divides PQ in the ratio 1:2. Therefore, by section formula, the coordinates of point A are given by
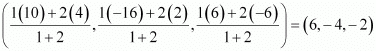
Point B divides PQ in the ratio 2:1. Therefore, by section formula, the coordinates of point B are given by
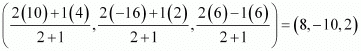
Thus, (6, –4, –2) and (8, –10, 2) are the points that trisect the line segment joining points P (4, 2, –6) and Q (10, –16, 6).
Question 69:
Three vertices of a parallelogram ABCD are A (3, –1, 2), B (1, 2, –4) andC (–1, 1, 2). Find the coordinates of the fourth vertex.
Answer
The three vertices of a parallelogram ABCD are given as A (3, –1, 2), B (1, 2, –4), and C (–1, 1, 2). Let the coordinates of the fourth vertex be D (x, y, z).
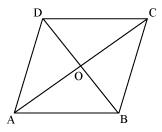
We know that the diagonals of a parallelogram bisect each other.
Therefore, in parallelogram ABCD, AC and BD bisect each other.
∴Mid-point of AC = Mid-point of BD
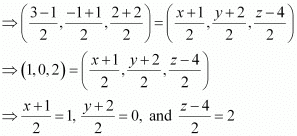
⇒ x = 1, y = –2, and z = 8
Thus, the coordinates of the fourth vertex are (1, –2, 8).
Question 70:
Find the lengths of the medians of the triangle with vertices A (0, 0, 6), B (0, 4, 0) and (6, 0, 0).
Answer
Let AD, BE, and CF be the medians of the given triangle ABC.
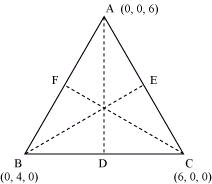
Since AD is the median, D is the mid-point of BC.
∴Coordinates of point D =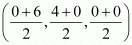 = (3, 2, 0)
= (3, 2, 0)
Since BE is the median. E is the mid-point of AC.
Since CF is the median, F is the mid-point of AB,
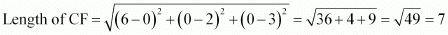
Thus, the lengths of the medians of ΔABC are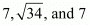 .
.
Question 71:
If the origin is the centroid of the triangle PQR with vertices P (2a, 2, 6), Q (–4, 3b, –10) and R (8, 14, 2c), then find the values of a, b and c.
Answer
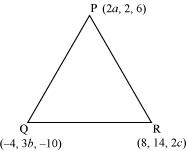
It is known that the coordinates of the centroid of the triangle, whose vertices are (x1, y1, z1), (x2, y2, z2) and (x3, y3, z3), are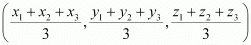 .
.
Therefore, coordinates of the centroid of ΔPQR
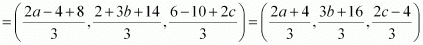
It is given that origin is the centroid of ΔPQR.
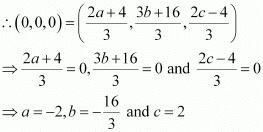
Thus, the respective values of a, b, and c are 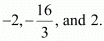
Question 72:
Find the coordinates of a point on y-axis which are at a distance of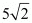 from the point P (3, –2, 5).
from the point P (3, –2, 5).
Answer
If a point is on the y-axis, then x-coordinate and the z-coordinate of the point are zero.
Let A (0, b, 0) be the point on the y-axis at a distance of 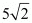 from point P (3, –2, 5). Accordingly,
from point P (3, –2, 5). Accordingly, 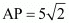
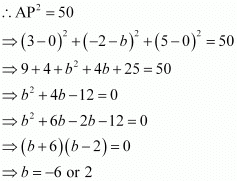
Thus, the coordinates of the required points are (0, 2, 0) and (0, –6, 0).
Question 73:
A point R with x-coordinate 4 lies on the line segment joining the pointsP (2, –3, 4) and Q (8, 0, 10). Find the coordinates of the point R.
[Hint suppose R divides PQ in the ratio k: 1. The coordinates of the point R are given by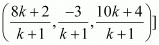
Answer
The coordinates of points P and Q are given as P (2, –3, 4) and Q (8, 0, 10).
Let R divide line segment PQ in the ratio k:1.
Hence, by section formula, the coordinates of point R are given by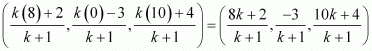
It is given that the x-coordinate of point R is 4.
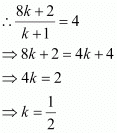
Therefore, the coordinates of point R are
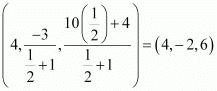
Question 74:
If A and B be the points (3, 4, 5) and (–1, 3, –7), respectively, find the equation of the set of points P such that PA2 + PB2 = k2, where k is a constant.
Answer
The coordinates of points A and B are given as (3, 4, 5) and (–1, 3, –7) respectively.
Let the coordinates of point P be (x, y, z).
On using distance formula, we obtain
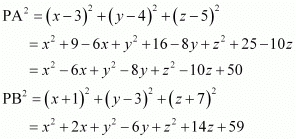
Now, if PA2 + PB2 = k2, then
Thus, the required equation is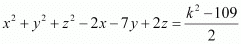 .
.
|
172 videos|503 docs|154 tests
|
FAQs on NCERT Solutions Class 12 Maths Chapter 11 - Three Dimensional Geometry
| 1. What are the basic concepts of three-dimensional geometry? |  |
| 2. How do you calculate the distance between two points in three-dimensional space? |  |
| 3. How do you find the equation of a plane in three-dimensional geometry? |  |
| 4. What is the concept of cross product in three-dimensional geometry? |  |
| 5. How do you determine the angle between two lines in three-dimensional space? |  |

















