Constructions, Class 10, Mathematics NCERT Solutions PDF Download
INTRODUCTION
In class IX, we have discussed a number of constructions with the help of ruler and compass e.g. bisecting a line segment, bisecting an angle, perpendicular bisector of line segment, some more constructions of triangles etc. with their justifications. In this chapter we will discuss more constructions by using the knowledge of the earlier construction.
DIVISION OF A LINE SEGMENT
Let us divide the given line segment in the given ratio say 5 : 8. This can be done in the following two ways:
(i) Use of Basic Proportionality Theorem.
(ii) Constructing a triangle similar to a given triangle.
Construction-1: Draw a segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two
parts.

Steps of Construction :
Step 1 : Draw any ray AX making an angle of 30° with AB.
Step 2 : Locate 13 points 



Step 3 : Join B with A13.
Step 4 : Through the point A5, draw a line A5C  A13B such that
A13B such that  AA5C = corr.
AA5C = corr.  AA13B intersecting AB
AA13B intersecting AB
at a point C. Then AC : CB = 5 : 8.
Let us see how this method gives us the required division.
Since A5C is parallel to A13 B

(Basic Proportionality Theorem)

This given that C divides AB in the ratio 5 : 8.
By measurement, we find, AC = 2.9 cm, CB = 4.7 cm.
By Calculation


Alternative Solution
Step 1 : Draw a line segment AB = 7.6 cm and to be divided in the ratio 5 : 8.
Step 2 : Draw any ray AX making an angle of 30° with AB.
Step 3 : Draw a ray BY parallel to AX by making  ABY equal to
ABY equal to  BAX. i.e.
BAX. i.e.  ABY = corr.
ABY = corr.  BAX.
BAX.

Step 4 : Locate the points A1, A2, A3, A3, A4, A5 on AX and B1, B2, B3, B4, B5, B6, B7, and B8 on BY
such that:
AA1 = A1A2 = .............. = A4A5 = BB1 = B1B2 = .................... = B6B7 = B7B8
Step 5 : Join A5B8. Let it intersect AB at a point C. Then AC : CB = 5 : 8.·

Construction-2 : Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are 7/5 of the corresponding sides of the first triangle
Sol. First of all we are to construct a triangle ABC with given sides, AB = 6 cm, BC = 7 cm, CA = 5 cm.
Given a triangle ABC, we are required to construct a triangle whose sides are 75 of the corresponding sides of ΔABC.
Steps of Construction :
Step 1 : Draw any ray BX making an angle of 30° with the base BC of ΔABC on the opposite side of the vertex A..
Step 2 : Locate seven points B1, B2, B3, B4, B5, B6 and B7 on BX so that
BB1 = B1B2 = B2B3 = B3B4 = B4B5 = B5B6 = B6B7·

[Note that the number of points should be greater of m and n in the scale factor m/n]
Step 3 : Join B5 (the fifth point) to C and draw a line through B7 parallel to B5C, intersecting the extended line segment BC at C'.
Step 4 : Draw a line through C' parallel to CA intersecting the extended line segment BA at A'.
Then, A'BC' is the required triangle.

Construction-3 : Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and  ABC = 60°. Then construct a triangle whose sides are 3/4 of the corresponding sides of the triangle ABC.
ABC = 60°. Then construct a triangle whose sides are 3/4 of the corresponding sides of the triangle ABC.
Sol. Given a triangle ABC, we are required to construct another triangle whose sides are 3/4
of the corresponding sides of the triangle ABC.

Steps of Construction :
Step 1 : Draw a line segment BC = 6 cm.
Step 2 : At B construct  CBY = 60° and cut off AB = 5 cm, join AB and AC. ABC is the required Δ.
CBY = 60° and cut off AB = 5 cm, join AB and AC. ABC is the required Δ.
Step 3 : Draw any ray BX making an acute angle say 30° with BC on the opposite side of the vertex
A,  CBX = 30° downwards.
CBX = 30° downwards.
Step 4 : Locate four (the greater of 3 and 4 in 3/4) points B1, B2, B3 and B4 on BX, so that BB1 =
B1B2 = B2B3 = B3B4.
Step 5 : Join B4C and draw a line through B3 (the 3rd point) parallel to B4C to intersect BC at C'.
Step 6 : Draw a line through C' parallel to the line CA to intersect BA at A'.
Then A'BC' is the required triangle whose each side is 3/4 times the corresponding sides of the ΔABC. Let us now see how this construction gives the required triangle.
For justification of the construction.

CONSTRUCTION OF TANGENTS TO A CIRCLE
a) If a point lies inside a circle, we can not draw any tangent to the circle i.e., No tangent is possible in this case.

b) If a point lies on the circle, then there is only one tangent to the circle at this point. The tangent to a circle at any point is perpendicular to the radius passing through the point of contact.

Two tangents are drawn from an external point to circle, they are equal in length.

Construction 4 : Draw a circle of radius 5 cm. From a point 8 cm away from its centre, construct pair of tangents to the circle measure their lengths.
Sol.

Steps of Construction :
Step-1 : Draw a circle with radius 5 cm whose centre is O.
Step-2 : Take a point P at a distance 8 cm from the centre O such that OP = 8cm.
Step-3 : Bisect the line segment OP at the point C such that OC =CP =4 cm.
Step-4 : Taking C as centre and OC as arc, draw a dotted circle to intersect the given circle at the points T and T'.
Step-5 : Join PT and PT'
PT and PT' are the required pair of tangents to the circle.
By measurement we obtain PT = PT' = 6.2 cm (Answer)

Construction 5. Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Sol.

Steps of Construction:
Step 1 : Draw two concentric circles with centre O and radii 4 cm and 6 cm such that OP = 6 cm, OQ = 4 cm.
Step 2 : Join OP and bisect it at M. i.e. M is the mid-point of OP i.e. OM = PM = 3 cm.
Step 3 : Taking M as centre with OM as radius draw a circle intersecting the smaller circle in two points namely T and S.
Step 4 : Join PT and PS.
PT and PS are the required tangents from a point P to the smaller circle, whose radius is 4 cm. By measurement:
PT = 4.5 cm.
Verification. OTP is right Δ at T
OP2 = OT2 + PT2
62 = 42 + PT2 PT2 = 36 – 16 = 20
PT2 = 36 – 16 = 20
PT = 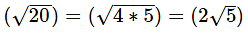 = 2 x 2.24 = 4.48 cm.
= 2 x 2.24 = 4.48 cm.
FAQs on Constructions, Class 10, Mathematics NCERT Solutions
| 1. What are the different types of constructions covered in Class 10 Mathematics? |  |
| 2. How can we construct a tangent to a circle from a point outside the circle? |  |
| 3. How can we construct a triangle given its three sides? |  |
| 4. How can we construct a circle passing through three non-collinear points? |  |
| 5. How can we construct a quadrilateral given its four sides and one diagonal? |  |

|
Explore Courses for Class 10 exam
|

|


















