NCERT Solutions Class 11 Maths Chapter 10 - Conic Sections
Q1: Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse 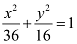
Ans: The given equation is 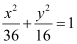 .
.
Here, the denominator of  is greater than the denominator of
is greater than the denominator of 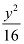 .
.
Therefore, the major axis is along the x-axis, while the minor axis is along the y-axis.
On comparing the given equation with 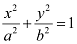 , we obtain a = 6 and b = 4.
, we obtain a = 6 and b = 4.
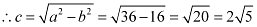
Therefore,
The coordinates of the foci are 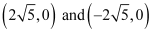 .
.
The coordinates of the vertices are (6, 0) and (–6, 0).
Length of major axis = 2a = 12
Length of minor axis = 2b = 8
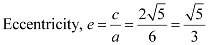
Length of latus rectum 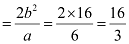
Q2: Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse 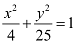
Ans: The given equation is 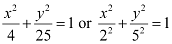 .
.
Here, the denominator of 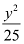 is greater than the denominator of
is greater than the denominator of 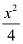 .
.
Therefore, the major axis is along the y-axis, while the minor axis is along the x-axis.
On comparing the given equation with 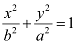 , we obtain b = 2 and a = 5.
, we obtain b = 2 and a = 5.
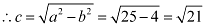
Therefore,
The coordinates of the foci are 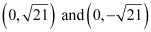 .
.
The coordinates of the vertices are (0, 5) and (0, –5)
Length of major axis = 2a = 10
Length of minor axis = 2b = 4
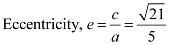
Length of latus rectum 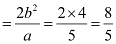
Q3: Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse 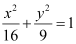
Ans: The given equation is 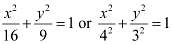 .
.
Here, the denominator of 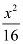 is greater than the denominator of
is greater than the denominator of 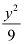 .
.
Therefore, the major axis is along the x-axis, while the minor axis is along the y-axis.
On comparing the given equation with 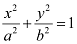 , we obtain a = 4 and b = 3.
, we obtain a = 4 and b = 3.
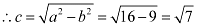
Therefore,
The coordinates of the foci are 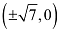 .
.
The coordinates of the vertices are 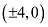 .
.
Length of major axis = 2a = 8
Length of minor axis = 2b = 6
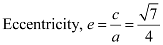
Length of latus rectum 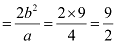
Q4: Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse 
Ans: The given equation is 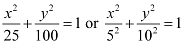 .
.
Here, the denominator of 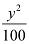 is greater than the denominator of
is greater than the denominator of 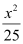 .
.
Therefore, the major axis is along the y-axis, while the minor axis is along the x-axis.
On comparing the given equation with 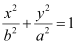 , we obtain b = 5 and a = 10.
, we obtain b = 5 and a = 10.

Therefore,
The coordinates of the foci are 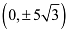 .
.
The coordinates of the vertices are (0, ±10).
Length of major axis = 2a = 20
Length of minor axis = 2b = 10

Length of latus rectum 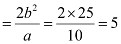
Q5: Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse 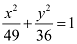
Ans: The given equation is 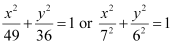 .
.
Here, the denominator of  is greater than the denominator of
is greater than the denominator of 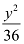 .
.
Therefore, the major axis is along the x-axis, while the minor axis is along the y-axis.
On comparing the given equation with 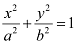 , we obtain a = 7 and b = 6.
, we obtain a = 7 and b = 6.
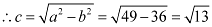
Therefore,
The coordinates of the foci are 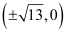 .
.
The coordinates of the vertices are (± 7, 0).
Length of major axis = 2a = 14
Length of minor axis = 2b = 12
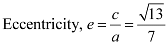
Length of latus rectum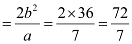
Q6: Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse 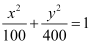
Ans: The given equation is 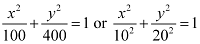 .
.
Here, the denominator of 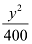 is greater than the denominator of
is greater than the denominator of 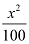 .
.
Therefore, the major axis is along the y-axis, while the minor axis is along the x-axis.
On comparing the given equation with 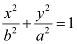 , we obtain b = 10 and a = 20.
, we obtain b = 10 and a = 20.
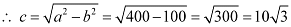
Therefore,
The coordinates of the foci are 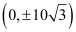 .
.
The coordinates of the vertices are (0, ±20)
Length of major axis = 2a = 40
Length of minor axis = 2b = 20

Length of latus rectum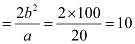
Q7: Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse 36x2 + 4y2 = 144
Ans: The given equation is 36x2 + 4y2 = 144.
It can be written as
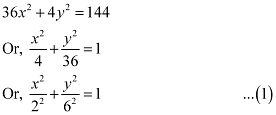
Here, the denominator of  is greater than the denominator of
is greater than the denominator of 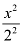 .
.
Therefore, the major axis is along the y-axis, while the minor axis is along the x-axis.
On comparing equation (1) with 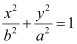 , we obtain b = 2 and a = 6.
, we obtain b = 2 and a = 6.
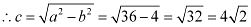
Therefore,
The coordinates of the foci are 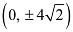 .
.
The coordinates of the vertices are (0, ±6).
Length of major axis = 2a = 12
Length of minor axis = 2b = 4
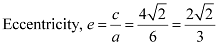
Length of latus rectum 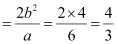
Q8: Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse 16x2 + y2 = 16
Ans: The given equation is 16x2 + y2 = 16.
It can be written as
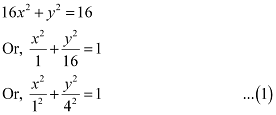
Here, the denominator of 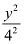 is greater than the denominator of
is greater than the denominator of 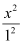 .
.
Therefore, the major axis is along the y-axis, while the minor axis is along the x-axis.
On comparing equation (1) with 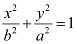 , we obtain b = 1 and a = 4.
, we obtain b = 1 and a = 4.
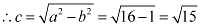
Therefore,
The coordinates of the foci are 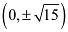 .
.
The coordinates of the vertices are (0, ±4).
Length of major axis = 2a = 8
Length of minor axis = 2b = 2

Length of latus rectum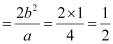
Q9: Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse 4x2 + 9y2 = 36
Ans: The given equation is 4x2 + 9y2 = 36.
It can be written as
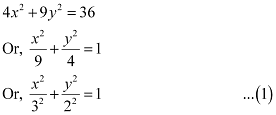
Here, the denominator of 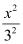 is greater than the denominator of
is greater than the denominator of 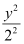 .
.
Therefore, the major axis is along the x-axis, while the minor axis is along the y-axis.
On comparing the given equation with 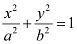 , we obtain a = 3 and b = 2.
, we obtain a = 3 and b = 2.
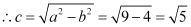
Therefore,
The coordinates of the foci are 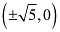 .
.
The coordinates of the vertices are (±3, 0).
Length of major axis = 2a = 6
Length of minor axis = 2b = 4
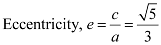
Length of latus rectum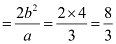
Q10: Find the equation for the ellipse that satisfies the given conditions: Vertices (±5, 0), foci (±4, 0)
Ans: Vertices (±5, 0), foci (±4, 0)
Here, the vertices are on the x-axis.
Therefore, the equation of the ellipse will be of the form 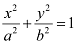 , where a is the semi-major axis.
, where a is the semi-major axis.
Accordingly, a = 5 and c = 4.
It is known that 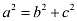 .
.
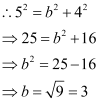
Thus, the equation of the ellipse is 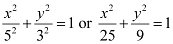 .
.
Q11: Find the equation for the ellipse that satisfies the given conditions: Vertices (0, ±13), foci (0, ±5)
Ans: Vertices (0, ±13), foci (0, ±5)
Here, the vertices are on the y-axis.
Therefore, the equation of the ellipse will be of the form 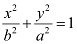 , where a is the semi-major axis.
, where a is the semi-major axis.
Accordingly, a = 13 and c = 5.
It is known that  .
.

Thus, the equation of the ellipse is  .
.
Q12: Find the equation for the ellipse that satisfies the given conditions: Vertices (±6, 0), foci (±4, 0)
Ans: Vertices (±6, 0), foci (±4, 0)
Here, the vertices are on the x-axis.
Therefore, the equation of the ellipse will be of the form 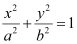 , where a is the semi-major axis.
, where a is the semi-major axis.
Accordingly, a = 6, c = 4.
It is known that 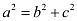 .
.
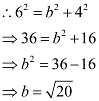
Thus, the equation of the ellipse is 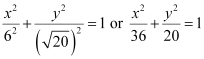 .
.
Q13: Find the equation for the ellipse that satisfies the given conditions: Ends of major axis (±3, 0), ends of minor axis (0, ±2)
Ans: Ends of major axis (±3, 0), ends of minor axis (0, ±2)
Here, the major axis is along the x-axis.
Therefore, the equation of the ellipse will be of the form 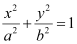 , where a is the semi-major axis.
, where a is the semi-major axis.
Accordingly, a = 3 and b = 2.
Thus, the equation of the ellipse is 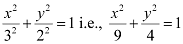 .
.
Q14: Find the equation for the ellipse that satisfies the given conditions: Ends of major axis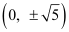 , ends of minor axis (±1, 0)
, ends of minor axis (±1, 0)
Ans: Ends of major axis  , ends of minor axis (±1, 0)
, ends of minor axis (±1, 0)
Here, the major axis is along the y-axis.
Therefore, the equation of the ellipse will be of the form 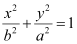 , where a is the semi-major axis.
, where a is the semi-major axis.
Accordingly, a = 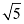 and b = 1.
and b = 1.
Thus, the equation of the ellipse is 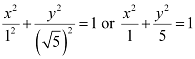 .
.
Q15: Find the equation for the ellipse that satisfies the given conditions: Length of major axis 26, foci (±5, 0)
Ans: Length of major axis = 26; foci = (±5, 0).
Since the foci are on the x-axis, the major axis is along the x-axis.
Therefore, the equation of the ellipse will be of the form 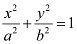 , where a is the semi-major axis.
, where a is the semi-major axis.
Accordingly, 2a = 26 ⇒ a = 13 and c = 5.
It is known that 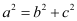 .
.
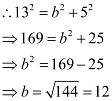
Thus, the equation of the ellipse is 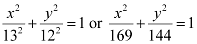 .
.
Q16: Find the equation for the ellipse that satisfies the given conditions: Length of minor axis 16, foci (0, ±6)
Ans: Length of minor axis = 16; foci = (0, ±6).
Since the foci are on the y-axis, the major axis is along the y-axis.
Therefore, the equation of the ellipse will be of the form  , where a is the semi-major axis.
, where a is the semi-major axis.
Accordingly, 2b = 16 ⇒ b = 8 and c = 6.
It is known that 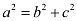 .
.
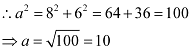
Thus, the equation of the ellipse is  .
.
Q17: Find the equation for the ellipse that satisfies the given conditions: Foci (±3, 0), a = 4
Ans: Foci (±3, 0), a = 4
Since the foci are on the x-axis, the major axis is along the x-axis.
Therefore, the equation of the ellipse will be of the form 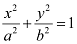 , where a is the semi-major axis.
, where a is the semi-major axis.
Accordingly, c = 3 and a = 4.
It is known that 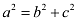 .
.
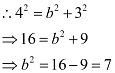
Thus, the equation of the ellipse is 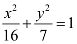 .
.
Q18: Find the equation for the ellipse that satisfies the given conditions: b = 3, c = 4, centre at the origin; foci on the x axis.
Ans: It is given that b = 3, c = 4, centre at the origin; foci on the x axis.
Since the foci are on the x-axis, the major axis is along the x-axis.
Therefore, the equation of the ellipse will be of the form 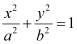 , where a is the semi-major axis.
, where a is the semi-major axis.
Accordingly, b = 3, c = 4.
It is known that 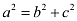 .
.
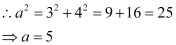
Thus, the equation of the ellipse is 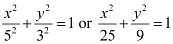 .
.
Q19: Find the equation for the ellipse that satisfies the given conditions: Centre at (0, 0), major axis on the y-axis and passes through the points (3, 2) and (1, 6).
Ans: Since the centre is at (0, 0) and the major axis is on the y-axis, the equation of the ellipse will be of the form
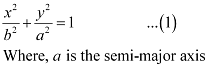
The ellipse passes through points (3, 2) and (1, 6). Hence,
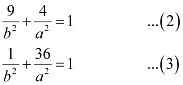
On solving equations (2) and (3), we obtain b2 = 10 and a2 = 40.
Thus, the equation of the ellipse is 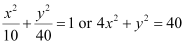 .
.
Q20: Find the equation for the ellipse that satisfies the given conditions: Major axis on the x-axis and passes through the points (4, 3) and (6, 2).
Ans: Since the major axis is on the x-axis, the equation of the ellipse will be of the form

The ellipse passes through points (4, 3) and (6, 2). Hence,
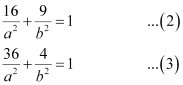
On solving equations (2) and (3), we obtain a2 = 52 and b2 = 13.
Thus, the equation of the ellipse is  .
.
|
75 videos|238 docs|91 tests
|
FAQs on NCERT Solutions Class 11 Maths Chapter 10 - Conic Sections
| 1. What are the different types of conic sections? |  |
| 2. How can I identify the type of conic section from its equation? |  |
| 3. What are the applications of conic sections in real life? |  |
| 4. How are conic sections related to the focus and directrix? |  |
| 5. Can conic sections be represented in polar coordinates? |  |

|
Explore Courses for Commerce exam
|

|

















