Fractions NCERT Solutions | Maths for Class 6 (Ganita Prakash) - New NCERT PDF Download
| Table of contents |

|
| Page 152 |

|
| Page 155 |

|
| Page 158 |

|
| Page 160 |

|
| Page 162 |

|
| Page 163 |

|
| Page 164 |

|
| Page 165 |

|
| Page 166 |

|
| Page 168 |

|
| Page 172 |

|
| Page 173 |

|
| Page 174 |

|
| Page 179 |

|
| Page 181 |

|
| Page 182 |

|
Page 152
Fill in the blanks with fractions.
Q1: Three guavas together weigh 1 kg. If they are roughly of the same size, each guava will roughly weigh ______kg.
Ans: 1/3
Q2: A wholesale merchant packed 1 kg of rice in four packets of equal weight. The weight of each packet is ____ kg.
Ans: 1/4
Q3: Four friends ordered 3 glasses of sugarcane juice and shared it equally among themselves. Each one drank ____ glass of sugarcane juice.
Ans: 3/4
Q4: The big fish weighs 1/2 kg. The small one weighs 1/4 kg. Together they weigh ____ kg.
Ans: 3/4
Q5: Arrange these fraction words in order of size from the smallest to the biggest in the empty box below: One and a half, three quarters, one and a quarter, half, quarter, two and a half.
Ans: One and a half means = 1 + 1/2 = 3/2, Three quarters means = 3/4, One and a quarter means = 1 + 1/4 = 5/4, Half means = 1/2, Quarter means = 1/4, Two and a half means = 2 + 1/2 = 5/2
Arrange these fractions from smallest to largest = 1/4 < 1/2 < 3/4 < 5/4 < 3/2 < 5/2.
So, let’s arrange these fraction words in order of size from smallest to larges,
Quarter < Half < Three quarters < One and a quarter < One and a half < Two and a half
Page 155
Q: The figures below show different fractional units of a whole chikki. How much of a whole chikki is each piece? Ans:
Ans:

Page 158
Q1: Continue this table of 1/2 for 2 more steps. Ans:
Ans: 
Q2: Can you create a similar table for 1/4?
Ans: 
Q3: Make 1/3 using a paper strip. Can you use this to also make 1/6?
Ans:  Yes, when you divide each part of this 1/3 it is 1/6.
Yes, when you divide each part of this 1/3 it is 1/6.
Q4: Draw a picture and write an addition statement as above to show:
a. 5 times 1/4 of a roti
Ans: 
b. 9 times 1/4 of a roti
Ans: 
Q5: Match each fractional unit with the correct picture: Ans:
Ans:
Page 160
Q1: On a number line, draw lines of lengths 1/10, 3/10, and 4/5.
Ans:
Q2: Write five more fractions of your choice and mark them on the number line.
Ans: Five fractions are = 1/5, 2/5, 5/10, 7/10 and 9/10
Q3: How many fractions lie between 0 and 1? Think, discuss with your classmates, and write your answer.
Ans: There are an infinite number of fractions between 0 and 1.
Example: 3/5, 7/10, 3/4, 1/2etc.
Q4: What is the length of the blue line and black line shown below? The distance between 0 and 1 is 1 unit long, and it is divided into two equal parts. The length of each part is 1/2. So the blue line is 1/2 units long. Write the fraction that gives the length of the black line in the box. Ans: Length of black line = ½ + ½ + ½ = 3/2
Ans: Length of black line = ½ + ½ + ½ = 3/2
Q5: Write the fraction that gives the lengths of the black lines in the respective boxes. Ans:
Ans:
Page 162
(a)
Q1: How many whole units are there in 7/2?
Ans: 
7 There are 3 whole units in 7/2.
Q2: How many whole units are there in 4/3 and in 7/3?
Ans:
(i) 
There are 1 whole unit in 4/3.
(ii) 
There are 2 whole units in 7/3.
(b)
Q1: Figure out the number of whole units in each of the following fractions:
(a) 8/3
Ans: 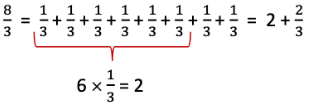
There are 2 whole units in 8/3.
(b) 11/5
Ans: 
There are 2 whole units in 11/5.
(c) 9/4
Ans: 
There are 2 whole units in 9/4.
Q2: Can all fractions greater than 1 be written as such mixed numbers?
Ans: Yes, all fractions greater than 1 can be written as mixed numbers. A mixed number consists of a whole number and a proper fraction (fraction less than 1).
Q3: Write the following fractions as mixed fractions (e.g.,  )
)
a. 9/2
Ans: 
b. 9/5
Ans:
c. 21/19
Ans: 
d. 47/9
Ans: 
e. 12/11
Ans:
f. 19/6
Ans:
Page 163
Q: Write the following mixed numbers as fractions:
Ans:

Page 164
Answer the following questions after looking at the fraction wall: Q1: Are the lengths 1/2 and 3/6 equal?
Q1: Are the lengths 1/2 and 3/6 equal?
Ans: Yes, here lengths 1/2 and 3/6 = 1/2
Lengths are equal.
Q2: Are 2/3 and 4/6 equivalent fractions? Why?
Ans: Yes, lengths 2/3 and 4/6 = 1/3 are equivalent fraction, as they have same length.
Q3: How many pieces of length 1/6 will make a length of 1/2?
Ans:
Total no. of pieces = 
Hence three pieces of length 1/6 will make a length of 1/2.
Q4: How many pieces of length 1/6 will make a length of 1/3?
Ans:
Total no. of pieces =
Hence two pieces of length 1/6 will make a length of 1/3.
Page 165
Q1: Are 3/6, 4/8, 5/10 equivalent fractions? Why?
Ans: 
Yes, 3/6, 4/8, 5/10 are equivalent fractions because they all simplify to 1/2.
Q2: Write two equivalent fractions for 2/6.
Ans: 
Therefore, 4/12, 6/18 are two equivalent fractions for 2/6
Q3:  (Write as many as you can)
(Write as many as you can)
Ans: 
Page 166
Q1: Three rotis are shared equally by four children. Show the division in the picture and write a fraction for how much each child gets. Also, write the corresponding division facts, addition facts and multiplication facts.
Fraction of roti each child gets is _________________ .
Division fact:
Addition fact:
Multiplication fact:
Compare your picture and answers with your classmates! Ans: As 3 rotis are divided equally among 4 children:
Ans: As 3 rotis are divided equally among 4 children:
(i) Each roti is divided into 4 equal parts.
(ii) Each child receives share from each roti.
Fraction of roti each child gets =
 Division fact:
Division fact:
3 wholes divided in 4 parts
3 ÷ 4 = 3/4
Addition fact:
Four times 3/4 added gives 3 wholes
= 3/4 + 3/4 + 3/4 + 3/4
= 12/4 = 3
Multiplication fact:
4 parts of 3/4 make 3 wholes
4 × 3/4 = 3
Q2: Draw a picture to show how much each child gets when 2 rotis are shared equally by 4 children. Also, write the corresponding division facts, addition facts, and multiplication facts. Ans: As 2 rotis have to be shared equally by 4 children we divide each roti in 4 parts and give
Ans: As 2 rotis have to be shared equally by 4 children we divide each roti in 4 parts and give
(a) 1 part of each roti to each child as shown below:
(b) 2 parts to each child as shown below
Division fact:
2 wholes divide in 4 parts
2 ÷ 4 or 2/4 = 12
Addition fact:
2/4 + 2/4 + 2/4 + 2/4 = 8/4 = 2
Multiplication fact:
4 × 2/4 = 2
Q3: Anil was in a group where 2 cakes were divided equally among 5 children. How much cake would Anil get? Ans: Anil is in a group where 2 cakes were divided equally among 5 children.
Ans: Anil is in a group where 2 cakes were divided equally among 5 children.
Each cake gets divided into 5 parts and Anil gets one part from each cake i.e. 1/5 + 1/5 = 2/5
Page 168
Q: Find the missing numbers:
a. 5 glasses of juice shared equally among 4 friends is the same as ____________ glasses of juice shared equally among 8 friends. 
Ans: Here, the amount of juice each friend gets when 5 glasses are shared among 4 friends = number of glasses number of friends = 5/4
Now to determine how many glasses of juice would be needed to give each of the 8 friends the same amount = 8 × 5/4 = 10 glasses
So, 10 glasses of juice shared equally among 8 friends is the same as 5 glasses of juice shared equally among 4 friends.
∴ 5/4 = 10/8
b. 4 kg of potatoes divided equally in 3 bags is the same as 12 kgs of potatoes divided equally in ____________ bags.
Ans: Let x is the number of bags for 12 kg of potatoes, where each bag has the same amount of potatoes then
12 kg/x bags = 4/3 kg per bag
⇒ 12 × 3 = 4 × x
⇒ 36 = 4x
⇒ x = 36/4
⇒ x = 9
∴ 4/3 = 12/9
c. 7 rods divided among 5 children is the same as rods divided among children. So, 75 = ____________
Ans: Dividing 7 rotis among 4 children gives 7 each child = 7/5 of a roti. We can find an equivalent fraction by multiplying both the numerator and the denominator by the same number. For example, multiplying both by 2.
So, 7 rotis divided among 5 children is the same as 14 rotis divided among 10 children
∴ 7/5 = 14/10
Page 172
Q: Find equivalent fractions for the given pairs of fractions such that the fractional units are the same.
a. 7/2 and 3/5
Ans: Given fractions are 7/2 and 3/5
Here, the denominators are 2 and 5.
And least common multiple of 2 and 5 is 10.
Hence for both fractions let’s have same denominator of 10.
Now for 7/2 multiply both the numerator and the denominator by 5.
And for 3/5 multiply both the numerator and the denominator by 2, we get,

Hence, the equivalent fractions with the same denominator are:
35/10 and 6/10
b. 8/3 and 5/6
Ans: Given fractions are 8/3 and 5/6
Here, the denominators are 3 and 6.
And least common multiple of 3 and 6 is 6.
Now for 8/3 multiply both the numerator and the denominator by 2.

5/6 already have a denominator 6.
Hence, the equivalent fractions with the same denominator are:
16/6 and 5/6
c. 3/4 and 3/5
Ans: Given fractions are 3/4 and 3/5
Here, the denominators are 4 and 5.
And least common multiple of 4 and 5 is 20.
Now for 3/4 multiply both the numerator and the denominator by 5.

And for 3/5 multiply both the numerator and the denominator by 4, we get

So, the equivalent fractions with the same denominator are:
15/20 and 12/20
d. 6/7 and 8/5
Ans: Given fractions are 6/7 and 8/5
Here, the denominators are 7 and 5.
And least common multiple of 7 and 5 is 35.
Now for 6/7 multiply both the numerator and the denominator by 5.

And for 8/5 multiply both the numerator and the denominator by 7, we get

So, the equivalent fractions with the same denominator are:
30/35 and 56/35
e. 9/4 and 5/2
Ans: Given fractions are 9/4 and 5/2
Here, the denominators are 4 and 2.
And least common multiple of 4 and 2 is 4.
Now for 5/2 multiply both the numerator and the denominator by 2.

and 9/4 already have a denominator 4
So, the equivalent fractions with the same denominator are:
9/4 and 10/4
f. 1/10 and 2/9
Ans: Given fractions are and 1/10 and 2/9
Here, the denominators are 10 and 9.
And least common multiple of 10 and 9 is 90.
Now for 1/10 multiply both the numerator and the denominator by 9.

And for 2 multiply both the numerator and the denominator by 10, we get

So, the equivalent fractions with the same denominator are:’
9/90 and 20/90
g. 8/3 and 11/4
Ans: Given fractions are 8/3 and 11/4
Here, the denominators are 3 and 4.
And least common multiple of 3 and 4 is 12.
Now for 8/3 multiply both the numerator and the denominator by 4.

And for 11/4 multiply both the numerator and the denominator by 3, we get

So, the equivalent fractions with the same denominator are:
32/12 and 33/12
h. 13/6 and 1/9
Ans: Given fractions are 13/6 and 1/9
Here, the denominators are 6 and 9.
And least common multiple of 6 and 9 is 18.
Now for 13/6 multiply both the numerator and the denominator by 3.

And for 1/9 multiply both the numerator and the denominator by 2, we get

So, the equivalent fractions with the same denominator are:
39/18 and 2/18
Page 173
Q: Express the following fractions in lowest terms:
a. 17/51
Ans: Here 51 is divisible by 17 then 51/17 = 3

which is the lowest term.
b. 64/144
Ans: Here 64 and 144 are both multiples of 16. So we divide both by 16.
c. 126/147
Ans: Here, 126/147

[∵ HCF of 126 and 147 is 7 × 3 = 21]

d. 525/112
Ans: Here 525 and 112 are both multiples of 7, we divide both by 7.
Page 174
Q1: Compare the following fractions and justify your answers:
a. 8/3, 5/2
Ans: L.C.M of 3 and 2 is 6.


b. 4/9, 3/7
Ans: Given fractions are 4/9 and 3/7.
Here LCM of denominators 9 and 7 is 63.
then multiplying and dividing 4/9 by 7 and 3/7 by 9 then

c. 7/10, 9/14
Ans: Given fractions are 7/10 and 9/14.
Here LCM of denominators 10 and 14 is 70.
then multiplying and dividing 7/10 by 7 and 9/14 by 5 then
d. 12/5, 8/5
Ans: Given fractions are 12/5, 8/5
Since, the denominators of both the fractions are same, then the fraction with the larger numerator is greater.
Here, 12/5 > 8/5
e. 9/4, 5/2
Ans: Given fractions are 9/4, 5/2.
Here LCM of denominators 4 and 2 is 4.
then multiplying and dividing 5/2 by 2 and
Equivalent fractions with 4 are 
9/4 < 10/4
∴ 9/4 < 5/2
Q2: Write following fractions in ascending order.
a. 7/10, 11/15, 2/5
Ans: The given fractions are 7/10, 11/15, 2/5
Let us find LCM of denominator 10, 15, 5
∴ LCM of 10, 15 and 5 = 2 × 3 × 5 = 30
Now let us make denominator of each fractions as LCM

Hence given fractions in ascending order are: 25,710115
b. 19/24, 5/6, 7/12
Ans: The given fractions are 19/24, 5/6, 7/12
Here LCM of 24, 6, 12 is 24.

On arranging in ascending Order, we get
14/24, 19/24, 20/24
⇒ 7/12, 19/24, 5/6
Q3: Write the following fractions descending order.
a. 25/16, 7/8, 13/4, 17/32
Ans: The given fractions are 25/16, 7/8, 13/4, 17/32
Let us find LCM of denominator 16, 8, 4, 32
LCM of 16, 8,4, 32 = 2 × 2 × 2 × 2 × 2 = 32
Now let us make denominator of each fractions as LCM thus

On arranging in descending order, we get

Hence given fractions in descending order are 13/4, 25/16, 7/8 and 17/32.
b. 3/4, 12/5, 7/12, 5/4
Ans: Given fractions are 3/4, 12/5, 7/12, 5/4
Here LCM of 4, 5, 12, 4 is 60
Now let us make denominator of each fraction as LCM then
Hence fractions in descending order are
12/5 > 5/4 > 3/4 > 7/12
Page 179
Q1: Add the following fractions using Brahmagupta’s method:
a. 
Ans: 
b. 
Ans: Here 
Here LCM of denominators 4 and 3 is 12
∴ Equivalent fraction of 3/4 with denominators 12 is 9/12 and equivalent fraction of 1/3 with denominators 12 is 4/12

c. 
Ans: Given
Now LCM of 3 and 6 is 6.
Expressing as equivalent fractions with denominators 6, we get
d. 
Ans: Here 
Now LCM of 3 and 7 is 21
Expressing as equivalent fractions with denominators 21, we get
To add , start by finding the least common denominator (LCD) of the two fractions. The denominators are 3 and 7, and their LCD is 21.
Next, rewrite each fraction with a denominator of 21.
is equivalent to , because .
is equivalent to , because .
Now that the fractions have the same denominator, add them together:
The final result is
e. 
Ans: Here 
Now LCM of 4, 3, 5 is 60.
Expressing as equivalent fractions with denominators 60, we get


f. 
Ans: Here 
Now LCM of 3 and 5 is 15
Expressing as equivalent fractions with denominators 15, we get


g. 
Ans: Here 
Now LCM of 5 and 3 is 15
Thus expressing as equivalent fractions with denominators 15, we get

h. 
Ans: Given 
Here LCM of 5 and 8 is 40
Expressing as equivalent fractions with denominators 40, we get
i. 
Ans: Here 
Now LCM of 2 and 4 is 4.
Expressing as equivalent fractions with denominators 4, we get


j. 
Ans: Given 
Here LCM of 3 and 7 is 21
Expressing as equivalent fractions with denominators 21, we get


k. 
Ans: Here 
Now LCM of 4, 3, 5 is 60
Expressing as equivalent fractions with denominators 60, we get


l. 
Ans: Here 
Now LCM of 3, 5 and 7 is 105.
Expressing as equivalent fractions with denominators 105, we get


m. 
Ans: Given 
Here LCM of 2, 4, 6 is 12.
Now expressing as equivalent fractions with denominators 12, we get

Q2: Rahim mixes 2/3 litres of yellow paint with 3/4 litres of blue paint to make green paint. What is the volume of green paint he has made?
Ans: Given quantity of yellow paint = 2/3 litres
and quality of blue paint = 3/4 litres
Volume of green paint made
= 2/3 litres + 3/4 litres
Here LCM of 3 and 4 is 12
Now expressing as equivalent fractions with denominator 12, we get


Q3: Geeta bought 2/5 meter of lace and Shamim bought 3/4 meter of the same lace to put a complete border on a table cloth whose perimeter is 1 meter long. Find the total length of the lace they both have bought. Will the lace be sufficient to cover the whole border?
Ans: Given length of lace bought by Geeta = 2/5 meter
and length of lace bought by Shamim = 3/4 meter
Total length of lace = 2/5 + 3/4
LCM of 5 and 4 is 20
Now expressing as equivalent fractions with denominator 20, we get
Total lace required = Perimeter = 1 m
Hence total lace Geeta and Shamim have together is sufficient to cover the whole border.
Page 181
Q1: 
Ans: 
Q2: 
Ans: 
Q3: 
Ans: 
Page 182
Q1: Carry out the following subtractions using Brahmagupta’s method:
a. 
Ans: Given 
Fractional unit for both fractions is 1/15 then
b. 
Ans: Given 
Here LCM of 5 and 15 is 15. Fractional unit for both fractions should be 1/15
c. 
Ans: Given 
Hence LCM of 6 and 9 is 18. Fractional unit for both fractions should be 1/18 then
d. 
Ans: Given 
Here LCM of 3 and 2 is 6. Fractional unit for both fractions should be 1/6
Q2: Subtract as indicated:
a. 
Ans: Given y – y
Here, LCM of 3 and 4 is 12.
Fractional unit for both fractions should be 1/12
b. 
Ans: Here, 
Now, LCM of 3 and 5 is 15.
Fractional unit = 1/15 for both fractions
Hence
c. 
Ans: Here fractional = 1/7 for both fractions.


Q3: Solve the following problems:
a. Java’s school is 7/10 km from her home. She takes an auto for 1/2 km from her home daily, and then walks the remaining distance to reach her school. How much does she walk daily to reach the school?
Ans: Given distance between Jaya’s school and home is 7/10 km and distance covered by Jaya in auto is 1/2 km.
∴ Distance Jaya covered by walking = 
LCM of 10 and 2 is 10.
Hence Jaya walks 1/5 km or 200 meters to reach her school.
b. Jeevika takes 10/3 minutes to take a complete round of the park and her 13 friend Namit takes 13/4 minutes to do the same. Who takes less time and by how much?
Ans: Time taken by Jeevika to cover 1 round of park = 10/3 mm
Time taken by Namit to cover 1 round of 13 park= 13/4 min
To find who takes less time we need to compare 10/3 and 13/4
Here, LCM of 3 and 4 is 12

[Expressing fractions in fractional unit 1/12]

Hence Namit takes less time
Namit takes 1/2 of minutes less than Jeevika.
|
2 videos|74 docs|19 tests
|
FAQs on Fractions NCERT Solutions - Maths for Class 6 (Ganita Prakash) - New NCERT
| 1. What are fractions and how are they represented? |  |
| 2. How do you add fractions with the same denominator? |  |
| 3. What is the process to subtract fractions with different denominators? |  |
| 4. How can fractions be simplified? |  |
| 5. What is the difference between proper and improper fractions? |  |
|
2 videos|74 docs|19 tests
|

|
Explore Courses for Class 6 exam
|

|

















