All Courses
Get the App Signup / Login
Sign in Open App
Commerce Exam  >  Commerce Notes  >  Mathematics (Maths) Class 11  >  NCERT Solutions: Introduction to Three Dimensional Geometry

Introduction to Three Dimensional Geometry NCERT Solutions | Mathematics (Maths) Class 11 - Commerce PDF Download

Exercise 11.1

Q1: A point is on the x-axis. What are its y-coordinate and z-coordinates?
Ans: If a point is on the x-axis, then the coordinates of y and z are 0.
So the point is (x, 0, 0).

Q2: A point is in the XZ-plane. What can you say about its y-coordinate?
Ans: If a point is in the XZ plane, then its y-co-ordinate is 0.

Q3: Name the octants in which the following points lie:
(1, 2, 3), (4, –2, 3), (4, –2, –5), (4, 2, –5), (– 4, 2, –5), (– 4, 2, 5), (–3, –1, 6) (2, –4, –7).
Ans: Here is the table which represents the octants:

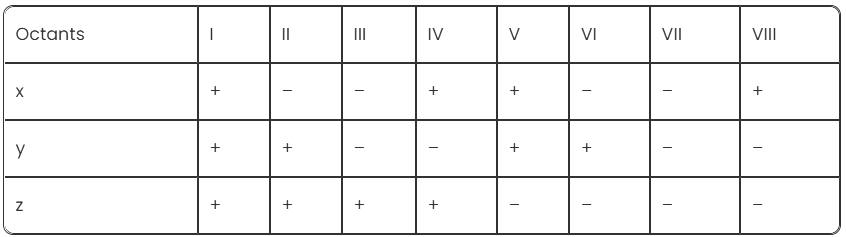
Introduction to Three Dimensional Geometry NCERT Solutions | Mathematics (Maths) Class 11 - Commerce

(i) (1, 2, 3)
Here, x is positive, y is positive, and z is positive.
So, it lies in the I octant.
(ii) (4, -2, 3)
Here, x is positive, y is negative, and z is positive.
So, it lies in the IV octant.
(iii) (4, -2, -5)
Here, x is positive, y is negative, and z is negative.
So, it lies in the VIII octant.
(iv) (4, 2, -5)
Here, x is positive, y is positive, and z is negative.
So, it lies in the V octant.
(v) (-4, 2, -5)
Here, x is negative, y is positive, and z is negative.
So, it lies in VI octant.
(vi) (-4, 2, 5)
Here, x is negative, y is positive, and z is positive.
So, it lies in the II octant.
(vii) (-3, -1, 6)
Here, x is negative, y is negative, and z is positive.
So, it lies in the III octant.
(viii) (2, -4, -7)
Here, x is positive, y is negative, and z is negative.
So, it lies in the VIII octant.

Q4: Fill in the blanks:
(i) The x-axis and y-axis, taken together, determine a plane known as _______.
(ii) The coordinates of points in the XY-plane are of the form _______.
(iii) Coordinate planes divide the space into ______ octants.
Ans: (i) The x-axis and y-axis, taken together, determine a plane known as XY Plane.
(ii) The coordinates of points in the XY-plane are of the form (x, y, 0).
(iii) Coordinate planes divide the space into eight octants.

Exercise 11.2

Q1: Find the distance between the following pairs of points:
(i) (2, 3, 5) and (4, 3, 1)
(ii) (–3, 7, 2) and (2, 4, –1)
(iii) (–1, 3, –4) and (1, –3, 4)
(iv) (2, –1, 3) and (–2, 1, 3)
Ans: (i) (2, 3, 5) and (4, 3, 1)
Let P be (2, 3, 5) and Q be (4, 3, 1)
By using the formula,
Distance PQ = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
So, here
x1 = 2, y1 = 3, z1 = 5
x2 = 4, y2 = 3, z2 = 1
Distance PQ = √[(4 – 2)2 + (3 – 3)2 + (1 – 5)2]
= √[(2)2 + 02 + (-4)2]
= √[4 + 0 + 16]
= √20
= 2√5
∴ The required distance is 2√5 units.

(ii) (–3, 7, 2) and (2, 4, –1)
Let P be (– 3, 7, 2) and Q be (2, 4, –1)
By using the formula,
Distance PQ = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
So, here
x1 = – 3, y1 = 7, z1 = 2
x2 = 2, y2 = 4, z2 = – 1
Distance PQ = √[(2 – (-3))2 + (4 – 7)2 + (-1 – 2)2]
= √[(5)2 + (-3)2 + (-3)2]
= √[25 + 9 + 9]
= √43
∴ The required distance is √43 units.

(iii) (–1, 3, –4) and (1, –3, 4)
Let P be (– 1, 3, – 4) and Q be (1, – 3, 4)
By using the formula,
Distance PQ = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
So here,
x1 = – 1, y1 = 3, z1 = – 4
x2 = 1, y2 = – 3, z2 = 4
Distance PQ = √[(1 – (-1))2 + (-3 – 3)2 + (4 – (-4))2]
= √[(2)2 + (-6)2 + (8)2]
= √[4 + 36 + 64]
= √104
= 2√26
∴ The required distance is 2√26 units.

(iv) (2, –1, 3) and (–2, 1, 3)
Let P be (2, – 1, 3) and Q be (– 2, 1, 3)
By using the formula,
Distance PQ = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
So here,
x1 = 2, y1 = – 1, z1 = 3
x2 = – 2, y2 = 1, z2 = 3
Distance PQ = √[(-2 – 2)2 + (1 – (-1))2 + (3 – 3)2]
= √[(-4)2 + (2)2 + (0)2]
= √[16 + 4 + 0]
= √20
= 2√5
∴ The required distance is 2√5 units.

Q2: Show that the points (–2, 3, 5), (1, 2, 3) and (7, 0, –1) are collinear.
Ans: If three points are collinear, then they lie on the same line.
First, let us calculate the distance between the 3 points
i.e., PQ, QR and PR
Calculating PQ
P ≡ (–2, 3, 5) and Q ≡ (1, 2, 3)
By using the formula,
Distance PQ = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
So, here
x1 = – 2, y1 = 3, z1 = 5
x2 = 1, y2 = 2, z2 = 3
Distance PQ = √[(1 – (-2))2 + (2 – 3)2 + (3 – 5)2]
= √[(3)2 + (-1)2 + (-2)2]
= √[9 + 1 + 4]
= √14
Calculating QR
Q ≡ (1, 2, 3) and R ≡ (7, 0, – 1)
By using the formula,
Distance QR = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
So, here
x1 = 1, y1 = 2, z1 = 3
x2 = 7, y2 = 0, z2 = – 1
Distance QR = √[(7 – 1)2 + (0 – 2)2 + (-1 – 3)2]
= √[(6)2 + (-2)2 + (-4)2]
= √[36 + 4 + 16]
= √56
= 2√14
Calculating PR
P ≡ (–2, 3, 5) and R ≡ (7, 0, – 1)
By using the formula,
Distance PR = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
So here,
x1 = –2, y1 = 3, z1 = 5
x2 = 7, y2 = 0, z2 = –1
Distance PR = √[(7 – (-2))2 + (0 – 3)2 + (-1 – 5)2]
= √[(9)2 + (-3)2 + (-6)2]
= √[81 + 9 + 36]
= √126
= 3√14
Thus, PQ = √14, QR = 2√14 and PR = 3√14
So, PQ + QR = √14 + 2√14
= 3√14
= PR
∴ The points P, Q and R are collinear.

Q3: Verify the following:
(i) (0, 7, –10), (1, 6, –6), and (4, 9, –6) are the vertices of an isosceles triangle.
(ii) (0, 7, 10), (–1, 6, 6), and (–4, 9, 6) are the vertices of a right-angled triangle.
(iii) (–1, 2, 1), (1, –2, 5), (4, –7, 8), and (2, –3, 4) are the vertices of a parallelogram.
Ans: (i) (0, 7, –10), (1, 6, –6), and (4, 9, – 6) are the vertices of an isosceles triangle.
Let us consider the points,
P(0, 7, –10), Q(1, 6, –6) and R(4, 9, –6)
If any 2 sides are equal, it will be an isosceles triangle
So, first, let us calculate the distance of PQ, QR
Calculating PQ
P ≡ (0, 7, – 10) and Q ≡ (1, 6, – 6)
By using the formula,
Distance PQ = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
So, here,
x1 = 0, y1 = 7, z1 = – 10
x2 = 1, y2 = 6, z2 = – 6
Distance PQ = √[(1 – 0)2 + (6 – 7)2 + (-6 – (-10))2]
= √[(1)2 + (-1)2 + (4)2]
= √[1 + 1 + 16]
= √18
Calculating QR
Q ≡ (1, 6, – 6) and R ≡ (4, 9, – 6)
By using the formula,
Distance QR = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
So, here
x1 = 1, y1 = 6, z1 = – 6
x2 = 4, y2 = 9, z2 = – 6
Distance QR = √[(4 – 1)2 + (9 – 6)2 + (-6 – (-6))2]
= √[(3)2 + (3)2 + (-6+6)2]
= √[9 + 9 + 0]
= √18
Hence, PQ = QR
18 = 18
2 sides are equal
∴ PQR is an isosceles triangle.

(ii) (0, 7, 10), (–1, 6, 6), and (–4, 9, 6) are the vertices of a right-angled triangle.
Let the points be
P(0, 7, 10), Q(– 1, 6, 6) & R(– 4, 9, 6)
First, let us calculate the distance of PQ, OR and PR
Calculating PQ
P ≡ (0, 7, 10) and Q ≡ (– 1, 6, 6)
By using the formula,
Distance PQ = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
So here,
x1 = 0, y1 = 7, z1 = 10
x2 = –1, y2 = 6, z2 = 6
Distance PQ = √[(-1 – 0)2 + (6 – 7)2 + (6 – 10)2]
= √[(-1)2 + (-1)2 + (-4)2]
= √[1 + 1 + 16]
= √18
Calculating QR
Q ≡ (1, 6, –6) and R ≡ (4, 9, –6)
By using the formula,
Distance QR = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
So, here
x1 = 1, y1 = 6, z1 = –6
x2 = 4, y2 = 9, z2 = –6
Distance QR = √[(4 – 1)2 + (9 – 6)2 + (-6 – (-6))2]
= √[(3)2 + (3)2 + (-6+6)2]
= √[9 + 9 + 0]
= √18
Calculating PR
P ≡ (0, 7, 10) and R ≡ (– 4, 9, 6)
By using the formula,
Distance PR = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
So, here
x1 = 0, y1 = 7, z1 = 10
x2 = – 4, y2 = 9, z2 = 6
Distance PR = √[(-4 – 0)2 + (9 – 7)2 + (6 – 10)2]
= √[(-4)2 + (2)2 + (-4)2]
= √[16 + 4 + 16]
= √36
Now,
PQ2 + QR2 = 18 + 18
= 36
= PR2
By using the converse of Pythagoras theorem,
∴ The given vertices P, Q & R are the vertices of a right–angled triangle at Q.

(iii) (–1, 2, 1), (1, –2, 5), (4, –7, 8), and (2, –3, 4) are the vertices of a parallelogram.
Let the points: A(–1, 2, 1), B(1, –2, 5), C(4, –7, 8) & D(2, –3, 4)
ABCD can be vertices of parallelogram only if opposite sides are equal.
i.e., AB = CD and BC = AD
First, let us calculate the distance
Calculating AB
A ≡ (–1, 2, 1) and B ≡ (1, –2, 5)
By using the formula,
Distance AB = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
So, here
x1 = – 1, y1 = 2, z1 = 1
x2 = 1, y2 = – 2, z2 = 5
Distance AB = √[(1 – (-1))2 + (-2 – 2)2 + (5 – 1)2]
= √[(2)2 + (-4)2 + (4)2]
= √[4 + 16 + 16]
= √36
= 6
Calculating BC
B ≡ (1, –2, 5) and C ≡ (4, –7, 8)
By using the formula,
Distance BC = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
So, here
x1 = 1, y1 = – 2, z1 = 5
x2 = 4, y2 = – 7, z2 = 8
Distance BC = √[(4 – 1)2 + (-7 – (-2))2 + (8 – 5)2]
= √[(3)2 + (-5)2 + (3)2]
= √[9 + 25 + 9]
= √43
Calculating CD
C ≡ (4, –7, 8) and D ≡ (2, –3, 4)
By using the formula,
Distance CD = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
So here,
x1 = 4, y1 = –7, z1 = 8
x2 = 2, y2 = –3, z2 = 4
Distance CD = √[(2 – 4)2 + (-3 – (-7))2 + (4 – 8)2]
= √[(-2)2 + (4)2 + (-4)2]
= √[4 + 16 + 16]
= √36
= 6
Calculating DA
D ≡ (2, –3, 4) and A ≡ (–1, 2, 1)
By using the formula,
Distance DA = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
So, here
x1 = 2, y1 = – 3, z1 = 4
x2 = –1, y2 = 2, z2 = 1
Distance DA = √[(-1 – 2)2 + (2 – (-3))2 + (1 – 4)2]
= √[(-3)2 + (5)2 + (-3)2]
= √[9 + 25 + 9]
= √43
Since AB = CD and BC = DA (given),
In ABCD, both pairs of opposite sides are equal.
∴ ABCD is a parallelogram.

Q4:  Find the equation of the set of points which are equidistant from the points (1, 2, 3) and (3, 2, –1).
Ans: Let A (1, 2, 3) & B (3, 2, –1)
Let point P be (x, y, z)
Since it is given that point P(x, y, z) is equal distance from point A(1, 2, 3) & B(3, 2, –1)
i.e. PA = PB
First, let us calculate
Calculating PA
P ≡ (x, y, z) and A ≡ (1, 2, 3)
By using the formula,
Distance PA = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
So, here
x1 = x, y1 = y, z1 = z
x2 = 1, y2 = 2, z2 = 3
Distance PA = √[(1 – x)2 + (2 – y)2 + (3 – z)2]
Calculating PB
P ≡ (x, y, z) and B ≡ (3, 2, –1)
By using the formula,
Distance PB = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
So, here
x1 = x, y1 = y, z1 = z
x2 = 3, y2 = 2, z2 = –1
Distance PB = √[(3 – x)2 + (2 – y)2 + (-1 – z)2]
Since PA = PB
Square on both sides, we get
PA2 = PB2
(1 – x)2 + (2 – y)2 + (3 – z)2 = (3 – x)2 + (2 – y)2 + (– 1 – z)2
(1 + x2 – 2x) + (4 + y2 – 4y) + (9 + z2 – 6z)
(9 + x2 – 6x) + (4 + y2 – 4y) + (1 + z2 + 2z)
– 2x – 4y – 6z + 14 = – 6x – 4y + 2z + 14
4x – 8z = 0
x – 2z = 0
∴ The required equation is x – 2z = 0.

Q5: Find the equation of the set of points P, the sum of whose distances from A(4, 0, 0) and B(–4, 0, 0) is equal to 10.
Ans: Let A(4, 0, 0) & B(– 4, 0, 0)
Let the coordinates of point P be (x, y, z)
Calculating PA
P ≡ (x, y, z) and A ≡ (4, 0, 0)
By using the formula,
Distance PA = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
So, here
x1 = x, y1 = y, z1 = z
x2 = 4, y2 = 0, z2 = 0
Distance PA = √[(4– x)2 + (0 – y)2 + (0 – z)2]
Calculating PB,
P ≡ (x, y, z) and B ≡ (– 4, 0, 0)
By using the formula,
Distance PB = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
So here,
x1 = x, y1 = y, z1 = z
x2 = – 4, y2 = 0, z2 = 0
Distance PB = √[(-4– x)2 + (0 – y)2 + (0 – z)2]
It is given that,
PA + PB = 10
PA = 10 – PB
Square on both sides, we get
PA2 = (10 – PB)2
PA2 = 100 + PB2 – 20 PB
(4 – x)2 + (0 – y)2 + (0 – z)2
100 + (– 4 – x)2 + (0 – y)2 + (0 – z)2 – 20 PB
(16 + x2 – 8x) + (y2) + (z2)
100 + (16 + x2 + 8x) + (y2) + (z2) – 20 PB
20 PB = 16x + 100
5 PB = (4x + 25)
Square on both sides again, we get
25 PB2 = 16x2 + 200x + 625
25 [(– 4 – x)2 + (0 – y)2 + (0 – z)2] = 16x2 + 200x + 625
25 [x2 + y2 + z2 + 8x + 16] = 16x2 + 200x + 625
25x2 + 25y2 + 25z2 + 200x + 400 = 16x2 + 200x + 625
9x2 + 25y2 + 25z2 – 225 = 0
∴ The required equation is 9x2 + 25y2 + 25z2 – 225 = 0.

The document Introduction to Three Dimensional Geometry NCERT Solutions | Mathematics (Maths) Class 11 - Commerce is a part of the Commerce Course Mathematics (Maths) Class 11.
All you need of Commerce at this link: Commerce
75 videos|238 docs|91 tests
Join Course for Free

Top Courses for Commerce

Related Exams
About this Document
4.92/5 Rating
Dec 23, 2024 Last updated
Document Description: NCERT Solutions: Introduction to Three Dimensional Geometry for Commerce 2024 is part of Mathematics (Maths) Class 11 preparation. The notes and questions for NCERT Solutions: Introduction to Three Dimensional Geometry have been prepared according to the Commerce exam syllabus. Information about NCERT Solutions: Introduction to Three Dimensional Geometry covers topics like Exercise 11.1, Exercise 11.2 and NCERT Solutions: Introduction to Three Dimensional Geometry Example, for Commerce 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for NCERT Solutions: Introduction to Three Dimensional Geometry.
Introduction of NCERT Solutions: Introduction to Three Dimensional Geometry in English is available as part of our Mathematics (Maths) Class 11 for Commerce & NCERT Solutions: Introduction to Three Dimensional Geometry in Hindi for Mathematics (Maths) Class 11 course. Download more important topics related with notes, lectures and mock test series for Commerce Exam by signing up for free. Commerce: Introduction to Three Dimensional Geometry NCERT Solutions | Mathematics (Maths) Class 11 - Commerce
Description
Full syllabus notes, lecture & questions for Introduction to Three Dimensional Geometry NCERT Solutions | Mathematics (Maths) Class 11 - Commerce - Commerce | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 11 | Best notes, free PDF download
Information about NCERT Solutions: Introduction to Three Dimensional Geometry
In this doc you can find the meaning of NCERT Solutions: Introduction to Three Dimensional Geometry defined & explained in the simplest way possible. Besides explaining types of NCERT Solutions: Introduction to Three Dimensional Geometry theory, EduRev gives you an ample number of questions to practice NCERT Solutions: Introduction to Three Dimensional Geometry tests, examples and also practice Commerce tests
75 videos|238 docs|91 tests
Join Course for Free
Download as PDF
Explore Courses for Commerce exam

Top Courses for Commerce

Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
10M+ students study on EduRev
Related Searches

pdf

,

Summary

,

study material

,

Important questions

,

Introduction to Three Dimensional Geometry NCERT Solutions | Mathematics (Maths) Class 11 - Commerce

,

video lectures

,

Objective type Questions

,

Viva Questions

,

Introduction to Three Dimensional Geometry NCERT Solutions | Mathematics (Maths) Class 11 - Commerce

,

practice quizzes

,

Introduction to Three Dimensional Geometry NCERT Solutions | Mathematics (Maths) Class 11 - Commerce

,

Exam

,

shortcuts and tricks

,

Previous Year Questions with Solutions

,

Semester Notes

,

mock tests for examination

,

past year papers

,

Extra Questions

,

ppt

,

Sample Paper

,

MCQs

,

Free

;
Additional Information about NCERT Solutions: Introduction to Three Dimensional Geometry for Commerce Preparation

NCERT Solutions: Introduction to Three Dimensional Geometry Free PDF Download

The NCERT Solutions: Introduction to Three Dimensional Geometry is an invaluable resource that delves deep into the core of the Commerce exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the NCERT Solutions: Introduction to Three Dimensional Geometry now and kickstart your journey towards success in the Commerce exam.

Importance of NCERT Solutions: Introduction to Three Dimensional Geometry

The importance of NCERT Solutions: Introduction to Three Dimensional Geometry cannot be overstated, especially for Commerce aspirants. This document holds the key to success in the Commerce exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

NCERT Solutions: Introduction to Three Dimensional Geometry Notes

NCERT Solutions: Introduction to Three Dimensional Geometry Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to NCERT Solutions: Introduction to Three Dimensional Geometry. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, NCERT Solutions: Introduction to Three Dimensional Geometry Notes on EduRev are your ultimate resource for success.

NCERT Solutions: Introduction to Three Dimensional Geometry Commerce Questions

The "NCERT Solutions: Introduction to Three Dimensional Geometry Commerce Questions" guide is a valuable resource for all aspiring students preparing for the Commerce exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study NCERT Solutions: Introduction to Three Dimensional Geometry on the App

Students of Commerce can study NCERT Solutions: Introduction to Three Dimensional Geometry alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the NCERT Solutions: Introduction to Three Dimensional Geometry, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of NCERT Solutions: Introduction to Three Dimensional Geometry is prepared as per the latest Commerce syllabus.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup