NCERT Solutions for Class 8 Maths - Linear Equations in One Variable (Exercise 2.1)

Exercise 2.1
Solve the following equations and check your results.Q1: 3x = 2x + 18
Sol: Transposing 2x from RHS to LHS, we have
3x – 2x = 18
⇒ x = 18
Putting the value of x in RHS and LHS we get,
3 × 18 = (2 × 18) +18
⇒ 54 = 54
⇒ LHS = RHS
Q2: 5t – 3 = 3t – 5
Sol: Transposing (–3) to RHS, we have
5t = 3t – 5 + 3
⇒ 5t = 3t – 2
Transposing 3t to LHS, we have
5t – 3t = –2
⇒ 2t = –2
Diving both sides by 2, we have
t = –1
Putting the value of t in RHS and LHS we get,
5 × (-1) – 3 = 3 × (-1) – 5
⇒ -5 – 3 = -3 – 5
⇒ -8 = -8
⇒ LHS = RHS
Q3: 5x + 9 = 5 + 3x
Sol: Transposing 9 to RHS, we have
5x = 5 + 3x – 9
⇒ 5x = –4 + 3x
Transposing 3x to LHS, we have
5x – 3x = –4
⇒ 2x = –4
Dividing both sides by 2, we have
x = -4/2 = -2
x = -2
Putting the value of x in RHS and LHS we get, 5× (-2) + 9 = 5 + 3× (-2)
⇒ -10 + 9 = 5 + (-6)
⇒ -1 = -1
⇒ LHS = RHS
Q4: 4z + 3 = 6 + 2z
Sol: Transposing 3 to RHS, we have
4z = 6 – 3 + 2z
⇒ 4z = 3 + 2z
Transposing 2z to LHS, we have
4z – 2z = 3
⇒ 2z = 3
Dividing both sides by 2, we have
z = 3/2
Putting the value of z in RHS and LHS we get,
(4 × 3/2) + 3 = 6 + (2 × 3/2)
⇒ 6 + 3 = 6 + 3
⇒ 9 = 9
⇒ LHS = RHS
Q5: 2x – 1 = 14 – x
Sol: Transposing (–1) to RHS, we have
2x = 14 – x + 1
⇒ 2x = 15 – x
Transposing (–x) to LHS, we have
2x + x = 15
⇒ 3x = 15
Dividing both sides by 3, we have
x = 15/3 = 5
∴ x = 5
Putting the value of x in RHS and LHS we get, (2×5) – 1 = 14 – 5
⇒ 10 – 1 = 9
⇒ 9 = 9
⇒ LHS = RHS
Q6: 8x + 4 = 3(x – 1) + 7
Sol: 8x + 4 = 3x – 3 + 7
⇒ 8x + 4 = 3x + 4
Transposing 4 to RHS, we have
8x = 3x + 4 – 4
Transposing 3x to LHS, we have
8x – 3x = 0
⇒ 5x = 0
∴ x = 0
Putting the value of x in RHS and LHS we get, (8×0) + 4 = 3 (0 – 1) + 7
⇒ 0 + 4 = 0 – 3 + 7
⇒ 4 = 4
⇒ LHS = RHS
Q7: 
Sol: Using distributive property,

⇒ 
Transposing  x to LHS, we have
x to LHS, we have 
⇒ 
⇒ x/5 = 8
Multiplying both sides by 5, we have
x = 8 × 5 = 40
∴ x = 40
Putting the value of x in RHS and LHS we get,
40 = 4/5 (40 + 10)
⇒ 40 = 4/5 × 50
⇒ 40 = 200/5
⇒ 40 = 40
⇒ LHS = RHS
Q8: 
Sol: Transposing 1 to RHS, we have
⇒ 
Transposing 7x/15 to LHS, we have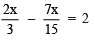
⇒ 
⇒ 3x/15 = 2
Multiplying both sides by 15, we have
3x = 2 × 15 = 30
Dividing both sides by 3, we have
∴ x = 10
Q9: 
Sol: Transposing 5/3 to RHS, we have
Transposing (–y) to LHS, we have 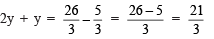
⇒ 3y = 7
Dividing both sides by 3, we have
3y = 3 = 7/3
∴ y = 7/3
Putting the value of y in RHS and LHS we get,
⇒ (2 × 7/3) + 5/3 = 26/3 – 7/3
⇒ 14/3 + 5/3 = 26/3 – 7/3
⇒ (14 + 5)/3 = (26 – 7)/3
⇒ 19/3 = 19/3
⇒ LHS = RHS
Q10: 3m = 5m - 8/5
Sol: Transposing 5m to LHS, we have
3m - 5m = - 8/5
⇒ -2m = -8/5
Dividing both sides by (–2), we have
∴ m = 4/5
Putting the value of m in RHS and LHS we get,
⇒ 3 × (4/5) = (5 × 4/5) – 8/5
⇒ 12/5 = 4 – (8/5)
⇒ 12/5 = (20 – 8)/5
⇒ 12/5 = 12/5
⇒ LHS = RHS.
Exercise: 2.2
Solve the following linear equations:Q1: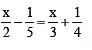
Sol: Transposing  to RHS and x/3 to LHS, we have
to RHS and x/3 to LHS, we have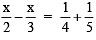
or
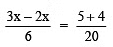
or
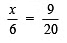
or
 (Multiplying both sides by 6)
(Multiplying both sides by 6)

Check: 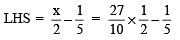

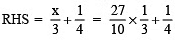

∴ LHS = RHS
Q2: 
Sol: ∵ LCM of 2, 4 and 6 = 12
∴ Multiplying both sides by 12, we have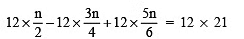
or
6n – 9n + 10n = 252
or
7n = 252
or
n = 252/7 = 36
∴ n = 36
Check: 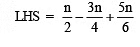
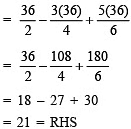
∴ LHS = RHS
Q3: 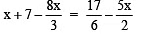
Sol: ∵ LCM of 3, 6 and 2 is 6.
∴ Multiplying both sides by 6, we have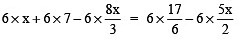
or 6x + 42 – 16x = 17 – 15x
or (6 – 16)x + 42 = 17 – 15x
or –10x + 42 = 17 – 15x
Transposing 42 to RHS and –15x to LHS, we have
–10x + 15x = 17 – 42 or 5x = –25
or
5x = –25
or
x = -25/5 = -5 (Dividing both sides by 5)
∴ x = –5
Check: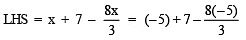

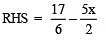
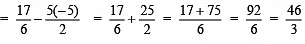
∴ LHS = RHS
Q4: 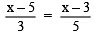
Sol: ∵ LCM of 3 and 5 is 15.
∴ Multiplying both sides by 15, we have
or
5(x – 5) = 3(x – 3)
or
5x – 25 = 3x – 9
Transposing (–25) to RHS and 3x to LHS, we have
5x – 3x = –9 + 25
or
2x = 16
or
x = 16/2 (Dividing both sides by 2)
∴ x = 8
Check:
= 3/3 = 1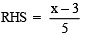
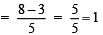
∴ LHS = RHS
Q5: 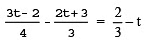
Sol: ∵ LCM of 4 and 3 is 12.
∴ Multiplying both sides by 12, we have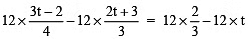
or
3(3t – 2) – 4(2t + 3) = (4 x2) – 12t
or
9t – 6 – 8t – 12 = 8 – 12t
or
(9 – 8)t – (6 + 12) = 8 – 12t
or
t – 18 = 8 – 12t
Transposing –18 to RHS and –12t to LHS, we have
t + 12t = 8 + 18
or
13t = 26
or
t = 26/13
∴ t = 2
Check: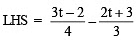
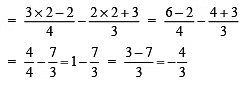
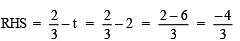
∴ LHS = RHS
Q6:
Sol: Since, LCM of 2 and 3 is 6.
∴ Multiplying both sides by 6, we have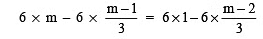
or
6m – 3(m – 1) = 6 – 2(m – 2)
or
6m – 3m + 3 = 6 – 2m + 4
or
(6 – 3)m + 3 = (6 + 4) – 2m
or
3m + 3 = 10 – 2m
Transposing 3 to RHS and –2m to LHS, we have
3m + 2m = 10 – 3
or 5m = 7
or
m = 7/5 (Dividing both sides by 5)
Check: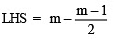
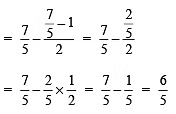
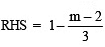
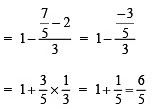
∴ LHS = RHS
Simplify and solve the following linear equations.
Q7: 3(t – 3) = 5(2t + 1)
Sol: 3(t – 3) = 5(2t + 1)
⇒ 3t – 9 = 10t + 5
⇒ 3t – 10t = 5 + 9
⇒ -7t = 14
⇒ t = 14/-7
⇒ t = -2
Q8: 15(y – 4) – 2(y – 9) + 5(y + 6) = 0
Sol: 15(y – 4) –2(y – 9) + 5(y + 6) = 0
⇒ 15y – 60 -2y + 18 + 5y + 30 = 0
⇒ 15y – 2y + 5y = 60 – 18 – 30
⇒ 18y = 12
⇒ y = 12/18
⇒ y = 2/3
Q9: 3 (5z – 7) – 2(9z – 11) = 4(8z – 13) – 17
Sol: 3(5z – 7) – 2(9z – 11) = 4(8z – 13) – 17
⇒ 15z – 21 – 18z + 22 = 32z – 52 – 17
⇒ 15z – 18z – 32z = -52 – 17 + 21 – 22
⇒ -35z = -70
⇒ z = -70/-35
⇒ z = 2
Q10: 0.25(4f – 3) = 0.05(10f – 9)
Sol: 0.25(4f – 3) = 0.05(10f – 9)
⇒ f – 0.75 = 0.5f – 0.45
⇒ f – 0.5f = -0.45 + 0.75
⇒ 0.5f = 0.30
⇒ f = 0.30/0.5
⇒ f = 3/5
⇒ f = 0.6
Old NCERT Questions
Solve the following equations
1.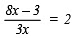
2. 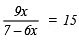
3. 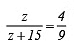
4.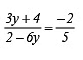
5. 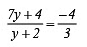
Sol:
1.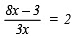
Multiplying both sides by 3x, we have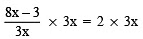
or
8x – 3 = 6x
Transposing (–3) to RHS and 6x to LHS, we have
8x – 6x = 3
or
2x = 3
Dividing both sides by 2, we have
x = 3/2
2.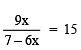
Multiplying both sides by 7 – 6x, we have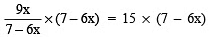
or
9x = 105 – 90x
Transposing (–90x) to LHS, we have
9x + 90x = 105
or
99x = 105
or
x = 105/99 (Dividing both sides by 99)
or
x = 35/33
3. 
By cross multiplication, we have
9z = 4(z + 15) ⇒ 9z = 4z + 60
Transposing 4z to LHS, we have
9z – 4z = 60
5z = 60 ⇒ z = 60/5 = 12
∴ z = 12
4. 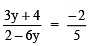
By cross multiplication, we have
5(3y + 4) = –2(2 – 6y)
or
15y + 20 = –4 + 12y
Transposing 20 to RHS and 12y to LHS, we have
15y – 12y = –4 – 20
or
3y = –24
or
y = - 24/3= –8 (Dividing both sides by 3)
or y = –8
5. 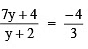
By cross multiplication, we have
3 * [7y + 4] = –4 x [y + 2]
or
21y + 12 = –4y – 8
Transposing 12 to RHS and (–4y) to LHS, we have
21y + 4y = –8 – 12
or
25y = –20
or
y = -20/25 (Dividing both sides by 25)
or
y = -20/25 = -4
∴ y = -4/5
Question 6: The ages of Hari and Harry are in the ratio 5: 7. Four years from now the ratio of their ages will be 3: 4. Find their present ages.
Sol: Let the present age of Hari = 5x years
and the present age of Harry = 7x years
After 4 years, Age of Hari = (5x + 4) years
Age of Harry = (7x + 4) years
According to the condition,
(5x + 4) : (7x + 4) = 3 : 4
or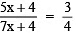
By cross multiplication, we have:
4(5x + 4) = 3(7x + 4)
or
20x + 16 = 21x + 12
Transposing 16 to RHS and 21x to LHS, we have
20x – 21x = 12 – 16
–x = –4
⇒ x = 4
∴ Present age of Hari = 5 * 4 = 20 years
Present age of Harry = 7 * 4 = 28 years
Question 7: The denominator of a rational number is greater than its numerator by 8. If the numerator is increased by 17 and the denominator is decreased by 1, the number obtained is 3/2. Find the rational number.
Sol: Let the numerator = x
∴ Denominator = x + 8
New numerator = (x) + 17
New denominator = (x + 8) – 1 = x + 7
∴ The new number =
According to the condition, we have 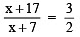
By cross multiplication, we have
2(x + 17) = 3(x + 7) 2x + 3x = 3x + 21
Transposing 34 to RHS and 3x to LHS, we have
2x – 34 = 21 – 34
⇒ –x = –13
∴ x= 13
⇒ Numerator = 13
x + 8 = 13 + 8 = 21
⇒Denominator = 21
∴ The rational number = 13/21
|
79 videos|408 docs|31 tests
|
FAQs on NCERT Solutions for Class 8 Maths - Linear Equations in One Variable (Exercise 2.1)
| 1. What are linear equations in one variable? |  |
| 2. How do you solve linear equations in one variable? |  |
| 3. What is the importance of solving linear equations in one variable? |  |
| 4. Can linear equations in one variable have more than one solution? |  |
| 5. How can linear equations in one variable be applied in real-life situations? |  |

|
Explore Courses for Class 8 exam
|

|


















