NCERT Solutions for Class 6 Maths - Mensuration
Exercise 10.1
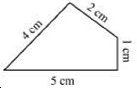
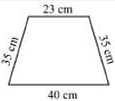
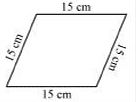
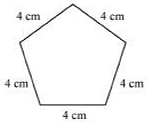
Q1. Find the perimeter of each of the following figures:
 |  |
| (a) | (b) |
 |  |
| (c) | (d) |
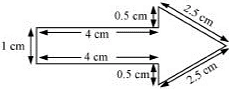 | 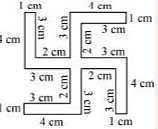 |
| (e) | (f) |
Ans:
(a) Perimeter
= Sum of all the sides
= 4 cm + 2 cm + 1 cm + 5 cm
= 12 cm
(b) Perimeter
= Sum of all the sides
= 23 cm + 35 cm + 40 cm + 35 cm
= 133 cm
(c) Perimeter
= Sum of all the sides
= 15 cm + 15 cm + 15 cm + 15 cm
= 60 cm
(d) Perimeter
= Sum of all the sides
= 4 cm + 4 cm + 4 cm + 4 cm + 4 cm
= 20 cm
(e) Perimeter
= Sum of all the sides
= 1 cm + 4 cm + 0.5 cm + 2.5 cm + 2.5 cm + 0.5 cm + 4 cm
= 15 cm
(f) Perimeter
= Sum of all the sides
= 4 cm + 1 cm + 3 cm + 2 cm + 3 cm + 4 cm + 1 cm + 3 cm + 2 cm + 3 cm + 4 cm + 1 cm + 3 cm + 2 cm + 3 cm + 4 cm + 1 cm + 3 cm + 2 cm + 3 cm
= 52 cm
Q2. The lid of a rectangular box of sides 40 cm by 10 cm is sealed all round with tape. What is the length of the tape required?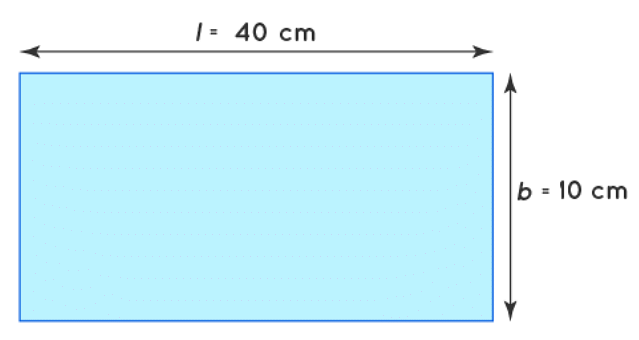
Ans: Total length of tape required = Perimeter of rectangle
= 2 (length + breadth)
= 2 (40 + 10)
= 2 x 50
= 100 cm
= 1 m
Thus, the total length of tape required is 100 cm or 1 m.
Q3. A table-top measures 2 m 25 cm by 1 m 50 cm. What is the perimeter of the table-top?
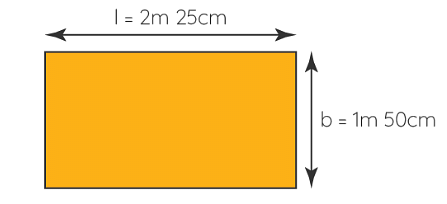
Ans: Length of table top = 2 m 25 cm = 2.25 m
Breadth of table top = 1 m 50 cm = 1.50 m
Perimeter of table top = 2 x (length + breadth)
= 2 x (2.25 + 1.50)
= 2 x 3.75
= 7.50 m
Thus, the perimeter of table top is 7.5 m.
Q4. What is the length of the wooden strip required to frame a photograph of length and breadth 32 cm and 21 cm respectively?
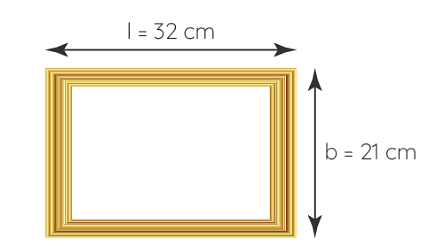
Ans: Length of wooden strip = Perimeter of photograph
Perimeter of photograph = 2 x (length + breadth)
= 2 (32 + 21)
= 2 x 53 cm
= 106 cm
Thus, the length of the wooden strip required is equal to 106 cm.
Q5. A rectangular piece of land measures 0.7 km by 0.5 km. Each side is to be fenced with 4 rows of wires. What is the length of the wire needed?
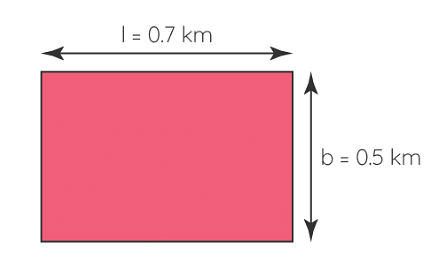
Ans: Since the 4 rows of wires are needed.
Therefore the total length of wires is equal to 4 times the perimeter of rectangle.
Perimeter of field = 2 x (length + breadth)
= 2 x (0.7 + 0.5)
= 2 x 1.2
= 2.4 km
= 2.4 x 1000 m
= 2400 m
Thus, the length of wire = 4 x 2400 = 9600 m = 9.6 km
Q6. Find the perimeter of each of the following shapes:
(a) A triangle of sides 3 cm, 4 cm and 5 cm.
(b) An equilateral triangle of side 9 cm.
(c) An isosceles triangle with equal sides 8 cm each and third side 6 cm
Ans: (a) Perimeter of ΔABC
= AB + BC + CA
= 3 cm + 5 cm + 4 cm
= 12 cm
(b) Perimeter of equilateral ABC
= 3 x side
= 3 x 9 cm
= 27 cm
(c) Perimeter of ΔABC
= AB + BC + CA
= 8 cm + 6 cm + 8 cm
= 22 cm
Q7. Find the perimeter of a triangle with sides measuring 10 cm, 14 cm and 15 cm.
Ans: Perimeter of triangle = Sum of all three sides
= 10 cm + 14 cm + 15 cm = 39 cm
Thus, the perimeter of triangle is 39 cm
Q8. Find the perimeter of a regular hexagon with each side measuring 8 m.
Ans: Perimeter of Hexagon = 6 x length of one side
= 6 x 8 m = 48 m
Thus, the perimeter of hexagon is 48 m.
Q9. Find the side of the square whose perimeter is 20 m.
Ans: Perimeter of square = 4 x side
Thus, the side of square is 5 cm.
Q10. The perimeter of a regular pentagon is 100 cm. How long is its each side?
Ans: Perimeter of regular pentagon = 100 cm
Thus, the side of regular pentagon is 20 cm.
Q11. A piece of string is 30 cm long. What will be the length of each side if the string is used to form:
(a) a square?
(b) an equilateral triangle?
(c) a regular hexagon?
Ans: Length of string = Perimeter of each figure
(a) Perimeter of square = 30 cm
Thus, the length of each side of square is 7.5 cm.
(b) Perimeter of equilateral triangle = 30 cm
Thus, the length of each side of equilateral triangle is 10 cm.
(c) Perimeter of hexagon = 30 cm
Thus, the side of each side of hexagon is 5 cm.
Q12. Two sides of a triangle are 12 cm and 14 cm. The perimeter of the triangle is 36 cm. What is its third side?
Ans: Let the length of third side be x cm.
Length of other two side are 12 cm and 14 cm.
Now, Perimeter of triangle = 36 cm
⇒ 12 +14 + x = 36
⇒ 26 + x= 36
⇒ x = 36- 26
⇒ x = 10 cm
Thus, the length of third side is 10 cm
Q13. Find the cost of fencing a square park of side 250 m at the rate of Rs 20 per metre.
Ans: Side of square = 250 m
Perimeter of square = 4 x side
= 4 x 250
= 1000 m
Since, cost of fencing of per meter = Rs 20
Therefore, the cost of fencing of 1000 meters = 20 x 1000 = Rs20,000
Q14. Find the cost of fencing a rectangular park of length 175 cm and breadth 125 m at the rate of Rs 12 per metre.
Ans: Length of rectangular park = 175 cm
Breadth of rectangular park = 125 m
Perimeter of park = 2 x (length + breadth)
= 2 x (175 + 125)
= 2 x 300 = 600 m
Since, the cost of fencing park per meter = Rs 12
Therefore, the cost of fencing park of 600 m = 12 x 600 = Rs 7,200
Q15. Sweety runs around a square park of side 75 m. Bulbul runs around a rectangular park with length 60 m and breadth 45 m. Who covers less distance?
Ans: Distance covered by Sweety = Perimeter of square park
Perimeter of square = 4 x side
= 4 x 75 = 300 m
Thus, distance covered by Sweety is 300 m.
Now, distance covered by Bulbul = Perimeter of rectangular park
Perimeter of rectangular park = 2 x (length + breadth)
= 2 x (60 + 45)
= 2 x 105 = 210 m
Thus, Bulbul covers the distance of 210 m and Bulbul covers less distance.
Q16. What is the perimeter of each of the following figures? What do you infer from the answers?
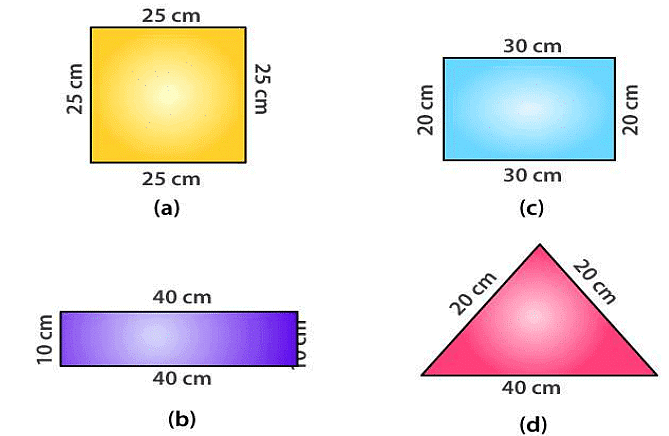
Ans:
(a) Perimeter of square
= 4 x side
= 4 x 25 = 100 cm
(b) Perimeter of rectangle
= 2 x (length + breadth) = 2 x (40 + 10) = 2 x 50 = 100 cm
(c) Perimeter of rectangle
= 2 x (length + breadth)
= 2 x (30 + 20) = 2 x 50 = 100 cm
(d) Perimeter of triangle = Sum of all sides
= 30 cm + 30 cm + 40 cm = 100 cm
Thus, all the figures have same perimeter.
Q17. Avneet buys 9 square paving slabs, each with a side of 1/2 m. He lays them in the form of a square.
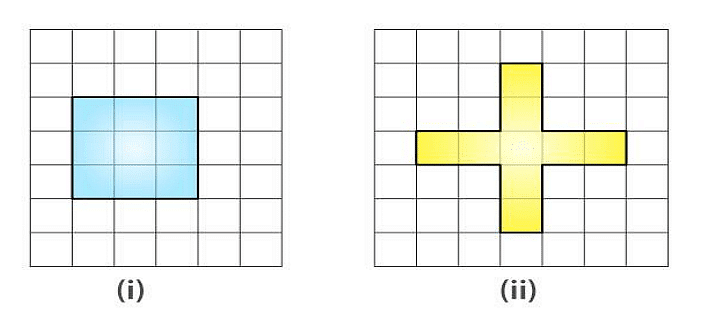
(a) What is the perimeter of his arrangement [Fig (i)]?
Ans: The arrangement so formed in Fig (i) is a square of side equal to 3 × side of the square slab
∴ Perimeter of his arrangement in Fig (i)
= 4 × ( 3 × side of the square slab)
= 4 × ( 3 × 0.5) m
= 4 × 1.5 m
= 6 m
(b) Shari does not like his arrangement. She gets him to lay them out like a cross. What is the perimeter of her arrangement [(Fig (ii)]?
Ans: The cross arrangement so formed in Fig (ii) by 9 square slabs, has perimeter, which consists of 20 length segments each equal to side of a square slab i.e. 0.5 m
∴ Perimeter of her arrangement in Fig (ii)
= 20 × ( side of the square slab)
= 20 × 0.5 m
= 10 m
(c) Which has greater perimeter?
Ans: The Cross arrangement has greater perimeter
(d) Avneet wonders if there is a way of getting an even greater perimeter. Can you find a way of doing this? (The paving slabs must meet along complete edges i.e. they cannot be broken.)
Ans: No, there is no way of getting perimeter greater than 10 m from any other possible arrangement formed by 9 square slabs when placed edge by edge completely.
Exercise 10.2
Q1. Find the areas of the following figures by counting squares:
(a) 
(b) 
(c) 
(d) 
(e) 
(f) 
(g) 
(h) 
(i) 
(j) 
(k) 
(l) 
(m) 
(n) 
Ans:
(a) Number of filled square = 9
∴ Area covered by squares = 9 x 1 = 9 sq. units
(b) Number of filled squares = 5
∴ Area covered by filled squares = 5 x 1 = 5 sq. units
(c) Number of full filled squares = 2
Number of half-filled squares = 4
∴ Area covered by full filled squares = 2 x 1 = 2 sq. units
And Area covered by half-filled squares = 
∴ Total area = 2 + 2 = 4 sq. units
(d) Number of filled squares = 8
∴ Area covered by filled squares = 8 x 1 = 8 sq. units
(e) Number of filled squares = 10
∴ Area covered by filled squares = 10 x 1 = 10 sq. units
(f) Number of full filled squares = 2
Number of half-filled squares = 4
∴ Area covered by full filled squares = 2 x 1 = 2 sq. units
And Area covered by half-filled squares = 
∴ Total area = 2 + 2 = 4 sq. units
(g) Number of full filled squares = 4
Number of half-filled squares = 4
∴ Area covered by full filled squares = 4 x 1 = 4 sq. units
And Area covered by half-filled squares = 
∴ Total area = 4 + 2 = 6 sq. units
(h) Number of filled squares = 5
∴ Area covered by filled squares = 5 x 1 = 5 sq. units
(i) Number of filled squares = 9
∴ Area covered by filled squares = 9 x 1 = 9 sq. units
(j) Number of full filled squares = 2
Number of half-filled squares = 4
∴ Area covered by full filled squares = 2 x 1 = 2 sq. units
And Area covered by half-filled squares = 
∴ Total area = 2 + 2 = 4 sq. units
(k) Number of full filled squares = 4
Number of half-filled squares = 2
∴ Area covered by full filled squares = 4 x 1 = 4 sq. units
And Area covered by half-filled squares 
∴ Total area = 4 + 1 = 5 sq. units
(l) Number of full filled squares = 3
Number of half-filled squares = 10
∴ Area covered by full filled squares = 3 x 1 = 3 sq. units
And Area covered by half-filled squares 
∴ Total area = 3 + 5 = 8 sq. units
(m) Number of full filled squares = 7
Number of half-filled squares = 14
∴ Area covered by full filled squares = 7 x 1 = 7 sq. units
And Area covered by half-filled squares 
∴ Total area = 7 + 7 = 14 sq. units
(n) Number of full filled squares = 10
Number of half-filled squares = 16
∴ Area covered by full filled squares = 10 x 1 = 10 sq. units
And Area covered by half-filled squares 
∴ Total area = 10 + 8 = 18 sq. units
Exercise 10.3
Q1. Find the areas of the rectangles whose sides are:
(a) 3 cm and 4 cm
(b) 12 m and 21 m
(c) 2 km and 3 km
(d) 2 m and 70 cm
Ans:
(a) Area of rectangle = length x breadth
= 3 cm x 4 cm = 12 cm2
(b) Area of rectangle = length x breadth
= 12 m x 21 m = 252 m2
(c) Area of rectangle = length x breadth
= 2 km x 3 km = 6 km2
(d) Area of rectangle = length x breadth
= 2 m x 70 cm
= 2 m x 0.7 m = 1.4 m2
Q2. Find the areas of the squares whose sides are:
(a) 10 cm
(b) 14 cm
(c) 5 m
Ans:
(a) Area of square = side x side = 10 cm x 10 cm = 100 cm2
(b) Area of square = side x side = 14 cm x 14 cm = 196 cm2
(c) Area of square = side x side = 5 m x 5 m = 25 m2
Q3. The length and breadth of three rectangles are as given below:
(a) 9 m and 6 m
(b) 17 m and 3 m
(c) 4 m and 14 m
Which one has the largest area and which one has the smallest?
Ans:
(a) Area of rectangle = length x breadth = 9 m x 6 m = 54 m2
(b) Area of rectangle = length x breadth= 3 m x 17 m = 51 m2
(c) Area of rectangle = length x breadth= 4 m x 14 m = 56 m2
Thus, the rectangle (c) has largest area, and rectangle (b) has smallest area.
Q4. The area of a rectangular garden 50 m long is 300 sq m. Find the width of the garden.
Ans:Length of rectangle = 50 m and Area of rectangle = 300 m2
Since, Area of rectangle = length x breadth
Therefore, 
Thus, the breadth of the garden is 6 m.
Q5. What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of Rs 8 per hundred sq m?
Ans: Length of land = 500 m and Breadth of land = 200 m
Area of land = length x breadth = 500 m x 200 m = 1,00,000 m2
Cost of tilling 100 sq. m of land = 8
∴ Cost of tilling 1,00,000 sq. m of land =  = 8000
= 8000
Q6. A table-top measures 2 m by 1 m 50 cm. What is its area in square metres?
Ans: Length of table = 2 m
Breadth of table = 1 m 50 cm = 1.50 m
Area of table = length x breadth
= 2 m x 1.50 m = 3 m2
Q7. A room is 4 m long and 3 m 50 cm wide. How many square metres of carpet is needed to cover the floor of the room?
Ans: Length of room = 4 m
Breadth of room = 3 m 50 cm = 3.50 m
Area of carpet = length x breadth
= 4 x 3.50 = 14m2
Q8: A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.
Ans: Length of floor = 5 m and breadth of floor = 4 m
Area of floor = length x breadth
= 5 m x 4 m = 20 m2 Now, Side of square carpet = 3 m
Area of square carpet = side x side = 3 x 3 = 9 m2
Area of floor that is not carpeted = 20 m2 – 9 m2 = 11 m2
Q9. Five square flower beds each of sides 1 m are dug on a piece of land 5 m long and 4 m wide. What is the area of the remaining part of the land?
Ans: Side of square bed = 1 m
Area of square bed = side x side = 1 m x 1 m = 1 m2
∴ Area of 5 square beds = 1 x 5 = 5 m2
Now, Length of land = 5 m
Breadth of land = 4 m
∴ Area of land = length x breadth = 5 m x 4 m = 20 m2
Area of remaining part = Area of land – Area of 5 flower beds
= 20 m2 – 5 m2 = 15 m2
Q10. By splitting the following figures into rectangles, find their areas (The measures are given in centimetres).

Ans:
(a)

Area of HKLM = 3 x 3 = 9 cm2
Area of IJGH = 1 x 2 = 2 cm2
Area of FEDG = 3 x 3 = 9 cm2
Area of ABCD = 2 x 4 = 8 cm2
Total area of the figure = 9 + 2 + 9 + 8 = 28 cm2
(b)

Area of ABCD = 3 x 1 = 3 cm2
Area of BDEF = 3 x 1 = 3 cm2
Area of FGHI = 3 x 1 = 3 cm2
Total area of the figure = 3 + 3 + 3 = 9 cm2
Q11. Split the following shapes into rectangles and find their areas. (The measures are given in centimetres)


Ans:
(a)

Area of rectangle ABCD = 2 x 10 = 20 cm2
Area of rectangle DEFG = 10 x 2 = 20 cm2
Total area of the figure = 20 + 20 = 40 cm2
(b)

There are 5 squares.
Each side is 7 cm
Area of 5 squares = 5 × 72
= 245 cm2
(c)

Area of rectangle ABCD = 5 x 1 = 5 cm2
Area of rectangle EFGH = 4 x 1 = 4 cm2
Total area of the figure = 5 + 4 cm2
Q12. How many tiles whose length and breadth are 12 cm and 5 cm respectively will be needed to fit in a rectangular region whose length and breadth are respectively:
(a) 100 cm and 144 cm
(b) 70 cm and 36 cm
Ans:
(a) Area of region = 100 cm x 144 cm = 14400 cm2
Area of one tile = 5 cm x 12 cm = 60 cm2
Thus, 240 tiles are required.
(b) Area of region = 70 cm x 36 cm = 2520 cm2
Area of one tile = 5 cm x 12 cm = 60 cm2
Thus, 42 tiles are required.
|
92 videos|348 docs|54 tests
|
FAQs on NCERT Solutions for Class 6 Maths - Mensuration
| 1. What is mensuration and why is it important? |  |
| 2. What are the different formulas used in mensuration? |  |
| 3. How can one improve their mensuration skills? |  |
| 4. What are some common mistakes to avoid while solving mensuration problems? |  |
| 5. What are some real-life applications of mensuration? |  |

|
Explore Courses for Class 6 exam
|

|


















