NCERT Solutions: Whole Numbers - Notes | Study Mathematics (Maths) Class 6 - Class 6

Whole numbers are a set of numbers including all positive integers and 0. Whole numbers are a part of real numbers that do not include fractions, decimals, or negative numbers.

Set of Whole Numbers

Let's have a look at NCERT Solutions from Exercise 2.1, Exercise 2.2 & Exercise 2.3

Q1. Write the next three natural numbers after 10999.
Ans: 

⇒ 10,999 + 1 = 11,000
⇒ 11,000 + 1 = 11,001
⇒ 11,001 + 1 = 11,002

Q2. Write the three whole numbers occurring just before 10001.
Ans: 

⇒ 10,001 – 1 = 10,000
⇒ 10,000 – 1 = 9,999
⇒ 9,999 – 1 = 9,998

Q3. Which is the smallest whole number?
Ans: ‘0’ (zero) is the smallest whole number.

Q4. How many whole numbers between 32 and 53?
Ans: 53 – 32 – 1 = 20 There are 20 whole numbers between 32 and 53.

Q5. Write the successor of:
(a) 2440701 
(b) 100199
(c) 1099999 
(d) 2345670
Ans: 

A successor is used for the numbers that comes just after any number.

(a) Successor of 2440701 is 2440701 + 1 = 2440702
(b) Successor of 100199 is 100199 + 1 = 100200
(c) Successor of 1099999 is 1099999 + 1 = 1100000
(d) Successor of 2345670 is 2345670 + 1 = 2345671

Q6. Write the predecessor of:
(a) 94 
(b) 10000
(c) 208090 
(d) 7654321
Ans: 

A predecessor is used for the numbers that comes just before any number.

(a) The predecessor of 94 is 94 – 1 = 93
(b) The predecessor of 10000 is 10000 – 1 = 9999
(c) The predecessor of 208090 is 208090 – 1 = 208089
(d) The predecessor of 7654321 is 7654321 – 1 = 7654320

Q7. In each of the following pairs of numbers, state which whole number is on the left of the other number on the number line. Also write them with the appropriate sign (>, <) between them.

(a) 530, 503 (b) 370, 307 (c) 98765, 56789 (d) 9830415, 10023001

Ans:

(a) Since, 530 > 503

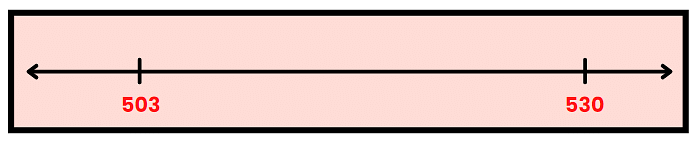
Hence, 503 is on the left side of 530 on the number line

(b) Since, 370 > 307

Hence, 307 is on the left side of 370 on the number line

(c) Since, 98765 > 56789

Hence, 56789 is on the left side of 98765 on the number line

(d) Since, 9830415 < 10023001

Hence, 9830415 is on the left side of 10023001 on the number line

Q8. Which of the following statements are true (T) and which are false (F)?
(a) Zero is the smallest natural number.
(b) 400 is the predecessor of 399.
(c) Zero is the smallest whole number.
(d) 600 is the successor of 599.
(e) All natural numbers are whole numbers.
(f) All whole numbers are natural numbers.
(g) The predecessor of a two-digit number is never a single-digit number.
(h) 1 is the smallest whole number.
(i) The natural number 1 has no predecessor.
(j) The whole number 1 has no predecessor.
(k) The whole number 13 lies between 11 and 12.
(l) The whole number 0 has no predecessor.
(m) The successor of a two-digit number is always a two-digit number.
Ans: 

(a) False

⇒ 0 is not a natural number.
(b) False

⇒ The predecessor of 399 is 398 Since, (399 – 1 = 398).
(c) True

⇒ Zero is the smallest whole number.
(d) True

⇒ Since (599 + 1 = 600).
(e) True

⇒ All natural numbers(1, 2, 3,....) are whole numbers(0, 1, 2, 3,.....).
(f) False

⇒ 0 is a whole number but is not a natural number.
(g) False

⇒ Example: the predecessor of 10 is 9.
(h) False

⇒ 0 is the smallest whole number.
(i) True

⇒ The predecessor of 1 is 0 but is not a natural number.
(j) False

⇒ 0 is the predecessor of 1 and is a whole number.
(k) False

⇒ 13 does not lie between 11 and 12.
(l) True

⇒ The predecessor of 0 is -1 and is not a whole number.
(m) False

⇒ As the successor of 99 is 100.

Q1. Find the sum by suitable rearrangement:
(a) 837 + 208 + 363 
(b) 1962 + 453 + 1538 + 647
Ans: 

(a) 837 + 208 + 363
= (837 + 363) + 208
= 1200 + 208
= 1408
(b) 1962 + 453 + 1538 + 647
= (1962 + 1538) + (453 + 647)
= 3500 + 1100
= 4600

Q2. Find the product by suitable rearrangement:
(a) 2 × 1768 × 50
(b) 4 × 166 × 25
(c) 8 × 291 × 125 
(d) 625 × 279 × 16
(e) 285 × 5 × 60 
(f) 125 × 40 × 8 × 25
Ans: 

(a) 2 x 1768 x 50
= (2 x 50) x 1768
= 100 x 1768
= 176800
(b) 4 x 166 x 25
= (4 x 25) x 166
= 100 x 166
= 16600
(c) 8 x 291 x 125
= (8 x 125) x 291
= 1000 x 291
= 291000
(d) 625 x 279 x 16
= (625 x 16) x 279
= 10000 x 279
= 2790000
(e) 285 x 5 x 60
= 284 x (5 x 60)
= 284 x 300
= 85500
(f) 125 x 40 x 8 x 25
= (125 x 8) x (40 x 25)
= 1000 x 1000
= 1000000

Q3. Find the value of the following:
(a) 297 × 17 + 297 × 3 
(b) 54279 × 92 + 8 × 54279
(c) 81265 × 169 − 81265 × 69 
(d) 3845 × 5 × 782 + 769 × 25 × 218
Ans: 

(a) 297 x 17 + 297 x 3
= 297 x (17 + 3)
= 297 x 20
= 5940
(b) 54279 x 92 + 8 x 542379
= 54279 x (92 + 8)
= 54279 x 100
= 5427900
(c) 81265 x 169 – 81265 x 69
= 81265 x (169 – 69)
= 81265 x 100
= 8126500
(d) 3845 x 5 x 782 + 769 x 25 x 218
= 3845 x 5 x 782 + 769 x 5 x 5 x 218
= 3845 x 5 x 782 + 3845 x 5 x 218
= 3845 x 5 x (782 + 218)
= 3845 x 5 x 1000
= 19225000

Q4. Find the product using suitable properties.
(a) 738 × 103 
(b) 854 × 102
(c) 258 × 1008 
(d) 1005 × 168
Ans:

(a) 738 x 103
= 738 x (100 + 3)
= 738 x 100 + 738 x 3
= 73800 + 2214
= 76014
(b) 854 x 102
= 854 x (100 + 2)
= 854 x 100 + 854 x 2
= 85400 + 1708
= 87108
(c) 258 x 1008
= 258 x (1000 + 8)
= 258 x 1000 + 258 x 8
= 258000 + 2064
= 260064
(d) 1005 x 168
= (1000 + 5) x 168
= 1000 x 168 + 5 x 168
= 168000 + 840
= 168840

Q5. A taxi driver filled his car petrol tank with 40 litres of petrol on Monday. The next day, he filled the tank with 50 litres of petrol. If the petrol costs Rs 44 per litre, how much did he spend in all on petrol?
Ans: Petrol filled on Monday = 40 litres
Petrol filled on next day = 50 litres
Total petrol filled = 90 litres
Now, Cost of 1 litre petrol = Rs. 44
Cost of 90 litres petrol = 44 x 90
= 44 x (100 – 10)
= 44 x 100 – 44 x 10
= 4400 – 440 = Rs. 3960
Therefore, he spent Rs. 3960 on petrol.

Q6. A vendor supplies 32 litres of milk to a hotel in the morning and 68 litres of milk in the evening. If the milk costs Rs 15 per litre, how much money is due to the vendor per day?
Ans: Supply of milk in morning = 32 litres
Supply of milk in evening = 68 litres
Total supply = 32 + 68 = 100 litres
Now Cost of 1 litre milk = Rs.15
Cost of 100 litres milk
= 15 x 100
= Rs. 1500
Therefore, Rs. 1500 is due to the vendor per day.

Q7. Match the following:

Ans:

Q1. Which of the following will not represent zero?

(a) 1 + 0 

(b) 0 × 0

(c) 0/2

(d) (10 - 10)/2

Ans: 

(a) 1 + 0 = 1

⇒ Hence, it does not represent zero

(b) 0 × 0 = 0

⇒ Hence, it represents zero

(c) 0 / 2 = 0

⇒ Hence, it represents zero

(d) (10 – 10) / 2 = 0 / 2 = 0

⇒ Hence, it represents zero

Q2. If the product of two whole numbers is zero, can we say that one or both of them will be zero? Justify through examples.

Ans: Yes, if we multiply any number with zero the resultant product will be zero.

Example: 2 x 0 = 0, 5 x 0 = 0, 9 x 0 = 0

If both numbers are zero, then the result will also be zero.

⇒ 0 x 0 = 0

Q3. If the product of two whole numbers is 1, can we say that one of both of them will be 1? Justify through examples.

Ans: If only one number be 1 then the product cannot be 1.

Examples: 5 x 1 = 5, 4 x 1 = 4, 8 x 1 = 8

If both number are 1, then the product is 1.

⇒ 1 x 1 = 1

Q4. Find using distributive property: 

(a) 728 x 101 

(b) 5437 x 1001 

(c) 824 x 25 

(d) 4275 x 125 

(e) 504 x 35

Ans: 

(a) 728 x 101

= 728 x (100 + 1)

= 728 x 100 + 728 x 1

= 72800 + 728

= 73528

(b) 5437 x 1001

= 5437 x (1000 + 1)

= 5437 x 1000 + 5437 x 1

= 5437000 + 5437

= 5442437

(c) 824 x 25

= 824 x (20 + 5)

= 824 x 20 + 824 x 5

= 16480 + 4120

= 20600

(d) 4275 x 125

= 4275 x (100 + 20 + 5)

= 4275 x 100 + 4275 x 20 + 4275 x 5

= 427500 + 85500 + 21375

= 534375

(e) 504 x 35

= (500 + 4) x 35

= 500 x 35 + 4 x 35

= 17500 + 140

= 17640

Q5. Study the pattern:

1 × 8 + 1 = 9 

12 × 8 + 2 = 98

123 × 8 + 3 = 987

1234 × 8 + 4 = 9876

12345 × 8 + 5 = 98765

Write the next two steps. Can you say how the pattern works?

(Hint: 12345 = 11111 + 1111 + 111 + 11 + 1).

Ans: 123456 × 8 + 6 = 987654

⇒ 1234567 × 8 + 7 = 9876543

Given:

⇒ 123456 = (111111 + 11111 + 1111 + 111 + 11 + 1)

⇒ 123456 × 8 = (111111 + 11111 + 1111 + 111 + 11 + 1) × 8

= 111111 × 8 + 11111 × 8 + 1111 × 8 + 111 × 8 + 11 × 8 + 1 × 8

= 888888 + 88888 + 8888 + 888 + 88 + 8

= 987648

⇒ 123456 × 8 + 6 = 987648 + 6

= 987654

Yes, here the pattern works.

1234567 × 8 + 7 = 9876543

Given:

1234567 = (1111111 + 111111 + 11111 + 1111 + 111 + 11 + 1)

1234567 × 8 = (1111111 + 111111 + 11111 + 1111 + 111 + 11 + 1) × 8

= 1111111 × 8 + 111111 × 8 + 11111 × 8 + 1111 × 8 + 111 × 8 + 11 × 8 + 1 × 8

= 8888888 + 888888 + 88888 + 8888 + 888 + 88 + 8

= 9876536

1234567 × 8 + 7 = 9876536 + 7

= 9876543

Yes, here the pattern works.