NCERT Solutions for Class 10 Maths Chapter 6 - Triangles (Exercise 6.4)
Q.1. Let ΔABC ~ ΔDEF and their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC.
Sol.
Given, ΔABC ~ ΔDEF,
Area of ΔABC = 64 cm2
Area of ΔDEF = 121 cm2
EF = 15.4 cm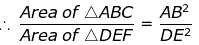
As we know, if two triangles are similar, ratio of their areas are equal to the square of the ratio of their corresponding sides,
= AC2/DF2 = BC2/EF2
∴ 64/121 = BC2/EF2
⇒ (8/11)2 = (BC/15.4)2
⇒ 8/11 = BC/15.4
⇒ BC = 8×15.4/11
⇒ BC = 8 × 1.4
⇒ BC = 11.2 cm
Q.2. Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
Sol.
Given, ABCD is a trapezium with AB || DC. Diagonals AC and BD intersect each other at point O.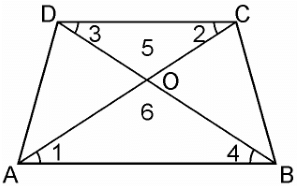
In ΔAOB and ΔCOD, we have
∠1 = ∠2 (Alternate angles)
∠3 = ∠4 (Alternate angles)
∠5 = ∠6 (Vertically opposite angle)
∴ ΔAOB ~ ΔCOD [AAA similarity criterion]
As we know, If two triangles are similar then the ratio of their areas are equal to the square of the ratio of their corresponding sides. Therefore,
Area of (ΔAOB)/Area of (ΔCOD) = AB2/CD2
= (2CD)2/CD2 [∴ AB = 2CD]
∴ Area of (ΔAOB)/Area of (ΔCOD)
= 4CD2/CD2 = 4/1
Hence, the required ratio of the area of ΔAOB and ΔCOD = 4:1
Q.3. In the figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that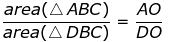
 Sol.
Sol.
Given, ABC and DBC are two triangles on the same base BC. AD intersects BC at O.
We have to prove: Area (ΔABC)/Area (ΔDBC) = AO/DO
Let us draw two perpendiculars AP and DM on line BC.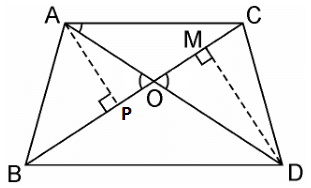 We know that area of a triangle = 1/2 × Base × Height
We know that area of a triangle = 1/2 × Base × Height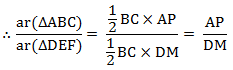
In ΔAPO and ΔDMO,
∠APO = ∠DMO (Each 90°)
∠AOP = ∠DOM (Vertically opposite angles)
∴ ΔAPO ~ ΔDMO (AA similarity criterion)
∴ AP/DM = AO/DO
⇒ Area (ΔABC)/Area (ΔDBC) = AO/DO.
Q.4. If the areas of two similar triangles are equal, prove that they are congruent.
Sol.
Say ΔABC and ΔPQR are two similar triangles and equal in area
Now let us prove ΔABC ≅ ΔPQR.
Since, ΔABC ~ ΔPQR
∴ Area of (ΔABC)/Area of (ΔPQR) = BC2/QR2
⇒ BC2/QR2 =1 [Since, Area(ΔABC) = (ΔPQR)
⇒ BC2/QR2
⇒ BC = QR
Similarly, we can prove that
AB = PQ and AC = PR
Thus, ΔABC ≅ ΔPQR [SSS criterion of congruence]
Q.5. D, E and F are respectively the mid-points of sides AB, BC and CA of ΔABC. Find the ratio of the areas of ΔDEF and ΔABC.
Sol.
Given, D, E and F are respectively the mid-points of sides AB, BC and CA of ΔABC.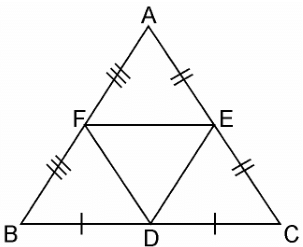
In ΔABC,
F is the mid-point of AB (Already given)
E is the mid-point of AC (Already given)
So, by the mid-point theorem, we have,
FE || BC and FE = 1/2BC
⇒ FE || BC and FE || BD [BD = 1/2BC]
Since, opposite sides of parallelogram are equal and parallel
∴ BDEF is parallelogram.
Similarly, in ΔFBD and ΔDEF, we have
FB = DE (Opposite sides of parallelogram BDEF)
FD = FD (Common sides)
BD = FE (Opposite sides of parallelogram BDEF)
∴ ΔFBD ≅ ΔDEF
Similarly, we can prove that
ΔAFE ≅ ΔDEF
ΔEDC ≅ ΔDEF
As we know, if triangles are congruent, then they are equal in area.
So,
Area(ΔFBD) = Area(ΔDEF) ………(i)
Area(ΔAFE) = Area(ΔDEF) ……….(ii)
and,
Area(ΔEDC) = Area(ΔDEF) …….(iii)
Now,
Area(ΔABC) = Area(ΔFBD) + Area(ΔDEF) + Area(ΔAFE) + Area(ΔEDC) ………(iv)
Area(ΔABC) = Area(ΔDEF) + Area(ΔDEF) + Area(ΔDEF) + Area(ΔDEF)
From equation (i), (ii) and (iii),
⇒ Area(ΔDEF) = (1/4)Area(ΔABC)
⇒ Area(ΔDEF)/Area(ΔABC) = 1/4
Hence, Area(ΔDEF): Area(ΔABC) = 1:4
Q.6. Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Sol.
Given: AM and DN are the medians of triangles ABC and DEF respectively and ΔABC ~ ΔDEF.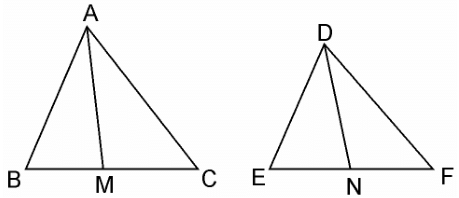
We have to prove: Area(ΔABC)/Area(ΔDEF) = AM2/DN2
Since, ΔABC ~ ΔDEF (Given)
∴ Area(ΔABC)/Area(ΔDEF) = (AB2/DE2) ………(i)
and, AB/DE = BC/EF = CA/FD …………(ii)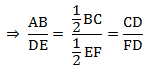
In ΔABM and ΔDEN,
Since ΔABC ~ ΔDEF
∴ ∠B = ∠E
AB/DE = BM/EN [Already Proved in equation (i)]
∴ ΔABC ~ ΔDEF [SAS similarity criterion]
⇒ AB/DE = AM/DN ………….(iii)
∴ ΔABM ~ ΔDEN
As the areas of two similar triangles are proportional to the squares of the corresponding sides.
∴ area(ΔABC)/area(ΔDEF) = AB2/DE2 = AM2/DN2
Hence, proved.
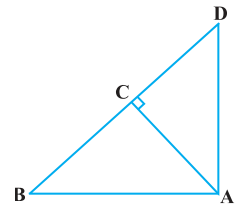
Q.7. Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Sol. 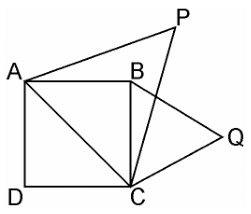
Given, ABCD is a square whose one diagonal is AC. ΔAPC and ΔBQC are two equilateral triangles described on the diagonals AC and side BC of the square ABCD.
Area(ΔBQC) = ½ Area(ΔAPC)
Since, ΔAPC and ΔBQC are both equilateral triangles, as per given,
∴ ΔAPC ~ ΔBQC [AAA similarity criterion]
∴ area(ΔAPC)/area(ΔBQC) = (AC2/BC2) = AC2/BC2
Since, Diagonal = √2 side = √2 BC = AC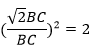
⇒ area(ΔAPC) = 2 × area(ΔBQC)
⇒ area(ΔBQC) = 1/2area(ΔAPC)
Hence, proved.
Q.8. ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(A) 2:1
(B) 1:2
(C) 4:1
(D) 1:4
Sol.
Given, ΔABC and ΔBDE are two equilateral triangle. D is the midpoint of BC.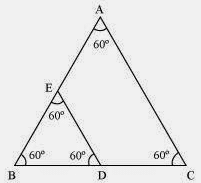 ∴ BD = DC = 1/2BC
∴ BD = DC = 1/2BC
Let each side of triangle is 2a.
As, ΔABC ~ ΔBDE
∴ Area(ΔABC)/Area(ΔBDE) = AB2/BD2 = (2a)2/(a)2 = 4a2/a2 = 4/1 = 4:1
Hence, the correct answer is (C).
Q.9. Sides of two similar triangles are in the ratio 4:9. Areas of these triangles are in the ratio
(A) 2:3
(B) 4:9
(C) 81:16
(D) 16:81
Sol.
Given, Sides of two similar triangles are in the ratio 4 : 9.
Let ABC and DEF are two similar triangles, such that,
ΔABC ~ ΔDEF
And AB/DE = AC/DF = BC/EF = 4/9
As, the ratio of the areas of these triangles will be equal to the square of the ratio of the corresponding sides,
∴ Area(ΔABC)/Area(ΔDEF) = AB2/DE2
∴ Area(ΔABC)/Area(ΔDEF) = (4/9)2 = 16/81 = 16:81
Hence, the correct answer is (D).
|
46 videos|182 docs|187 tests
|
FAQs on NCERT Solutions for Class 10 Maths Chapter 6 - Triangles (Exercise 6.4)
| 1. How do I find the length of the third side of a triangle if I know the lengths of the other two sides? |  |
| 2. What is the Pythagorean theorem and how is it used to solve triangle problems? |  |
| 3. Can two different triangles have the same area? |  |
| 4. What is the sum of the angles in a triangle? |  |
| 5. How can I determine if three given side lengths form a triangle? |  |

















