NCERT Solutions for Class 8 Maths Chapter 5 - Squares and Square Roots (Exercise 5.4)
Exercise 5.4
Q1. Find the square root of each of the following numbers by the Division method.
(i) 2304
(ii) 4489
(iii) 3481
(iv) 529
(v) 3249
(vi) 1369
(vii) 5776
(viii) 7921
(ix) 576
(x) 1024
(xi) 3136
(xii) 900
Ans:
(i)
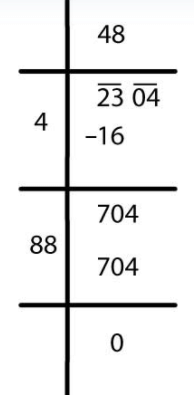
√2304 = 48
(ii)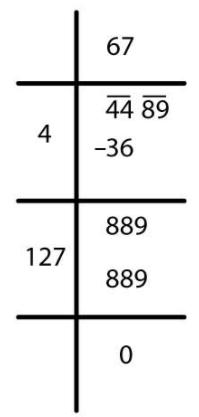
√4489 = 67
(iii)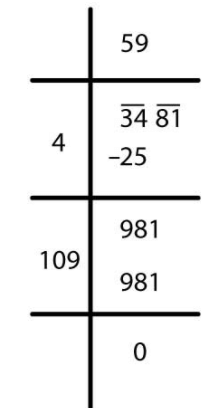
√3481 = 59
(iv)
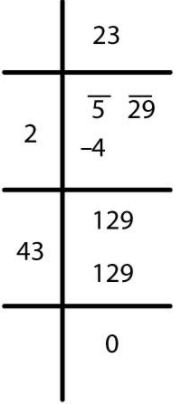
√529 = 23
(v)
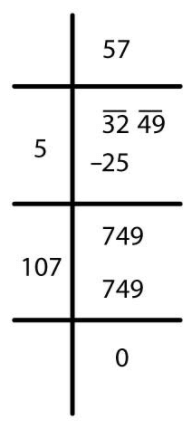
√3249 = 57
(vi)
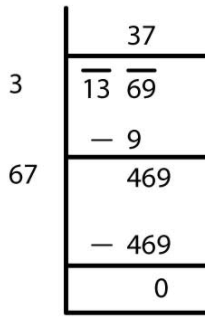
√1369 = 37
(vii)
√5776 = 76
(viii)
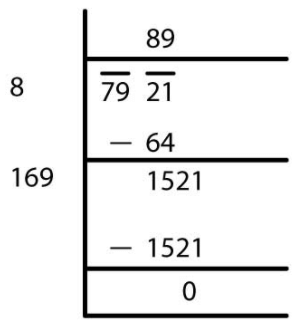
√7291 = 89
(ix)

√576 = 24
(x)

√1024 = 32
(xi)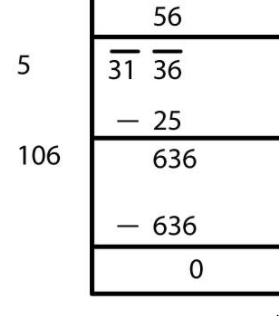
√3136 = 56
(xii)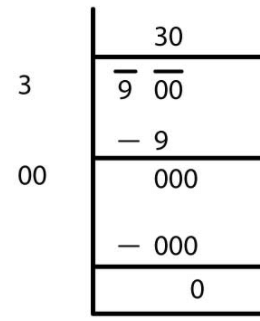
√900 = 30
Q2. Find the number of digits in the square root of each of the following numbers (without any calculation).
(i) 64
(ii) 144
(iii) 4489
(iv) 27225
(v) 390625
Ans: If ‘n’ stands for the number of digits in the given number, then
(i) For 64, n = 2 [even number]
∴ Number of digit is its square root = n/2 = 2/2 = 1
(ii) For 144, n = 3 [odd number]
∴ Number of digits in its square root = n+1/2 = 3+1/2 = 4/2 = 2
(iii) For 4489, n = 4 [even number]
∴ Number of digits in its square root = n/2 = 4/2 = 2
(iv) For 27225, n = 5 [odd number]
∴ Number of digits in its square root = n+1/2 = 5+1/2 = 6/2 = 3
(v) For 390625, n = 6 [even number]
∴ Number of digits in its square root = n/2 =6/2 =3
Q3. Find the square root of the following decimal numbers.
(i) 2.56
(ii) 7.29
(iii) 51.84
(iv) 42.25
(v) 31.36
Ans: (i) √2.56
Here, number of decimal places, are already even.
∴ We mark off the periods and find the square root.
∴ √2.56 = 1.6
(ii) √7.29
Here, number of decimal places are already even.
Therefore, we mark off the periods and find the square root.
∴ √7.29 = 2.7
(iii) √51.84
Here, the decimal places are already even.
∴ We mark off the periods and find the square root.
∴ √51.84 = 7.2
(iv) √42.25
Here, the decimal places are already even.
∴ We mark off periods and find the square root.
∴ √42.25 = 6.5
(v) √31.36
Here, the decimal places are already even.
∴ We mark off the periods and find the square root.
∴ √31.36 = 5.6
Q4. Find the least number which must be subtracted from each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.
(i) 402
(ii) 1989
(iii) 3250
(iv) 825
(v) 4000
Ans:
(i) On proceeding to find the square root of 402, we have since we get a remainder 2
∴ The required least number to be subtracted from 402 is 2.
∴ 402 – 2 = 400, and √400 = 20
(ii) Since, we get a remainder of 53
∴ The least number to be subtracted from the given number = 53
1989 – 53 = 1936, and √1936 = 44
(iii) Since, we get a remainder 1.
∴ The smallest number to be subtracted from the given number = 1
Now, 3250 – 1 = 3249, and 

(iv) Since, we get a remainder 41.
∴ The required smallest number to be subtracted from the given number = 41
Now, 825 – 41 = 784, and 

(v) Since, we get a remainder 31,
∴ The required smallest number to be subtracted from the given number = 31
Now, 4000 – 31 = 3969, and 

Q5. Find the least number which must be added to each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.
(i) 525
(ii) 1750
(iii) 252
(iv) 1825
(v) 6412
Ans:
(i) Since, we get a remainder 41.
i.e. 525 > 222.
and next square number is 23.
∴ The required number to be added = 232 – 525
= 529 – 525 = 4
Now, 525 + 4 = 529, and 

(ii) Since, we get a remainder 69.
i.e. 1750 > (41)2
and next square number is 422.
∴ The required number to be added = 422 – 1750
= 1764 – 1750 = 14
Now, 1750 + 14 = 1764, and 

(iii) Since, we get a remainder 27.
Since, 252 > (15)2 and next square number = 16
∴ The required number to be added = 162 – 252
= 256 – 252 = 4
Now, 252 + 4 = 256, and 

(iv) Since, we get a remainder, 61.
∴ 1825 > (42)2
∵ Next square number = 43
∴ The required number to be added = (43)2 – 1825
= 1849 – 1825 = 24
Now, 1825 + 24 = 1849, and 

(v) Since, we get a remainder 12.
∴ 6412 > (80)2
∵ Next square number = 81
∴ Required number to be added = (81)2 – 6412
= 6561 – 6412 = 149
Now, 6412 + 149 = 6561 and 

Q6. Find the length of the side of a square whose area is 441 m2.
Ans: Let the side of the square = x metre
∴ Area = side * side
= x * x = x2 metre2
Thus, the required side is 21 m.
Q7. In a right triangle ABC, ∠B = 90°.
(a) If AB = 6 cm, BC = 8 cm, find AC.
(b) If AC = 13 cm, BC = 5 cm, find AB.
Ans:

Remember
I. In a right triangle, the longest side is called the hypotenuse.
II. (Hypotenuse)2 = [Sum of the squares of other two sides]
(a) ∵ ∠B = 90°
∴ Hypotenuse = AC
∴ AC2 = AB2 + BC2
= 82 + 62
= 64 + 36 = 100
AC = 10
Thus, AC = 10 cm
(b) Here ∠B = 90°
∴ Hypotenuse = AC
∵ AC2 = AB2 + BC2
or 132 = AB2 + 52
or AB2 = 132 – 52
= 169 – 25 = 144
Now 
or AB = 12
Thus, AB = 12 cm

Q8. A gardener has 1000 plants. He wants to plant these so that the number of rows and the number of columns remain the same. Find the minimum number of plants he needs more for this.
Ans: Since the number of plants in a row and the number of columns are the same.
∴ Their product must be a square number.
∵ Th gardener has 1000 plants.
∴ 1000 is not a perfect square, and (31)2 < 1000
(∵ There is a remainder of 39).
Obviously the next square number = 32
∴ Number of plants required to be added = (32)2 – 1000
= 1024 – 1000 = 24
Q9. There are 500 children in a school. For a P.T. drill they have to stand in such a manner that the number of rows is equal to number of columns. How many children would be left out in this arrangement.
Ans: Since the number of rows and the number of columns are same.
∴ The total number (i.e. their product) must be a square number, we have Since, we get a remainder of 16
∴ 500 > (22)2 or 500 – 16 = (22)2
Thus, the required number of children to be left out = 16
Deleted Questions from NCERT
Finding square root by division method- For larger numbers, we use the division method for finding their square roots. This requires the pre estimation of a number of digits in the square root.
- We know that the smallest 3-digit perfect square number is 100, which is the square of 10 (2-digit number).
- The greatest 3-digit perfect number is 961, which is the square of 31 (2-digit number).
- The greatest 4-digit perfect number is 9801, which is the square of 99 (2-digit number).
- We can say that “if a perfect square is a 3-digit or 4-digit number, then its square root will have 2-digits.”
 Division Method
Division Method
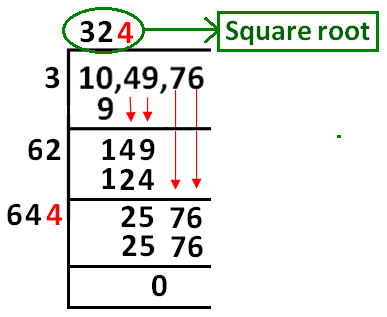
Example: Find the square root of 1369.
Solution.
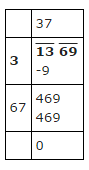
√1369 = 37
Think, Discuss, WriteQ.1. Can we say that if a perfect square is of n-digits, then its square root will have n/2 digits if n is even or (n+1)/2 if n is odd?
Solution. Yes, it is true.
Examples:
(i) 529 (a perfect number), n = 3 (odd number)
∴ Number of digits in square root = n+1/2
= 3+1/2 = 2
Also, square root of 529 = 23 (2-digits).
(ii) 1296 (is perfect square) and n = 4 (even number)
∴ Number of digits of its square root = n/2 = 4/2 =2
Now √1296 = 36 (2-digits).
Q.2. Without calculating square roots, find the number of digits in the square root of the following numbers.
(i) 25600
(ii) 100000000
(iii) 36864
Solution.
(i) 25600
∵ n = 5 [an odd number]
∴ Its square root will have (n+1)/2 digits,
i.e, 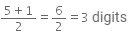
(ii) 100000000
∵ n = 9 → odd number
∴ Number of digits of its square root = n+1/2
= 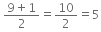
(iii) 36864
∵ n = 5 → odd number
∴ Number of digits in its square root = n+1/2
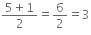
Q.3. Estimate the value of the following to the nearest whole number.
(i) √80
(ii) √1000
(iii) √350
(iv) √500
Solution.
(i) √80
∵ 102 = 100, 92 = 81, 82 = 64
and 80 is between 64 and 81.
i.e. 64 < 80 < 81
or 82 < 80 < 92
or 8 < √80 < 9
Thus, √80 lies between 8 and 9.
(ii) √1000
We know that
302 = 900, 312 = 961, 322 = 1024
∴ 1000 lies between 961 and 1024.
i.e. 916 < 1000 < 1024
or 312 < 1000 < 322
or 31 < √1000 < 32
Thus,√1000 lies between 31 and 32.
(iii) √350
We have 182 = 324, 192 = 361
Since, 350 lies between 324 and 316.
or 324 < 350 < 361
or 182 < 350 < 192
or 18 < √350 < 19
Thus, √350 lies between 18 and 19.
(iv) √500
∵ 222 = 484 and 232 = 529
Since, 500 lies between 484 and 529.
or 484 < 500 < 529
or 222 < 500 < 232
or 22 < √500 < 23
∴ √500 lies between 22 and 23.
|
90 docs|16 tests
|

|
Explore Courses for Class 8 exam
|

|