NCERT Solutions for Class 8 Maths - Symmetry- 2
Exercise 14.3
Question 1:
Name any two figures that have both line symmetry and rotational symmetry.
Answer 1:
Circle and Square.
Question 2:
Draw, wherever possible, a rough sketch of:
(i) a triangle with both line and rotational symmetries of order more than 1.
(ii) a triangle with only line symmetry and no rotational symmetry of order more than 1.
(iii) a quadrilateral with a rotational symmetry of order more than 1 but not a line symmetry.
(iv) a quadrilateral with line symmetry but not a rotational symmetry of order more than 1.
Answer 2:
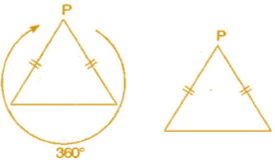
(i) An equilateral triangle has both line and rotational symmetries of order more than 1.
Line symmetry:
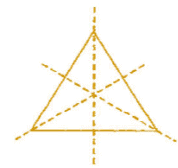
Rotational symmetry:
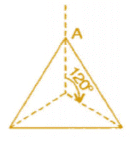
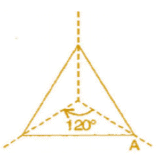
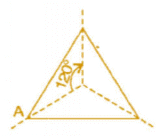
(ii) An isosceles triangle has only one line of symmetry and no rotational symmetry of order more than 1.
Line symmetry:
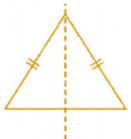
Rotational symmetry:
(iii) A quadrilateral with no line of symmetry is an irregular quadrilateral
Checking rotational symmetry
If it is rotated 90°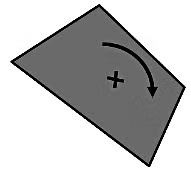
It does not looks same as initial figure
If it is rotated 180°

It does not looks same as initial figure
If it is rotated 360°

It looks same as initial figure
Thus,
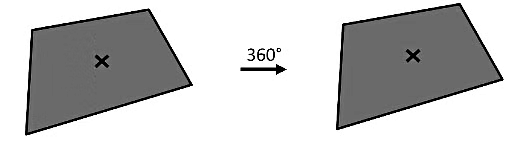
Thus, order of rotational symmetry - 1
Hence,
A quadrilateral with a rotational symmetry of order not a line of symmetry Is not possible
(iv) A trapezium which has equal non-parallel sides, a quadrilateral with line symmetry but not a rotational symmetry of order more than 1.
Line symmetry:
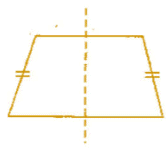
Rotational symmetry:
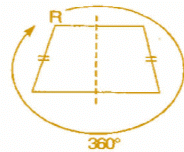
Question 3:
In a figure has two or more lines of symmetry, should it have rotational symmetry of order more than 1?
Answer 3:
Yes, because every line through the centre forms a line of symmetry and it has rotational symmetry around the centre for every angle.
Question 4:
Fill in the blanks:
Shape | Centre of Rotation | Order of Rotation | Angle of Rotation |
Square |
|
| |
Rectangle |
|
| |
Rhombus |
|
| |
Equilateral triangle |
|
| |
Regular hexagon |
|
| |
Circle |
|
| |
| Semi-circle |
Answer 4:
Shape | Centre of Rotation | Order of Rotation | Angle of Rotation |
Square | Intersecting point of diagonals. | 4 | 90° |
Rectangle | Intersecting point of diagonals. | 2 | 180° |
Rhombus | Intersecting point of diagonals. | 2 | 180° |
Equilateral triangle | Intersecting point of medians. | 3 | 120° |
Regular hexagon | Intersecting point of diagonals. | 6 | 60° |
Circle | Centre | infinite | At every point |
Semi-circle | Mid-point of diameter | 1 | 360° |
Question 5:
Name the quadrilateral which has both line and rotational symmetry of order more than 1.
Answer 5:
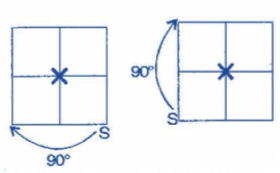
Square has both line and rotational symmetry of order more than 1.
Line symmetry: 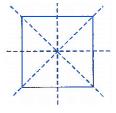
Rotational symmetry:
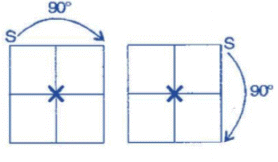
Question 6:
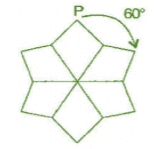
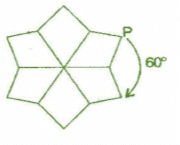
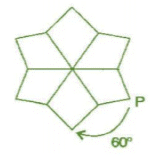
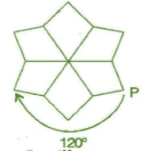
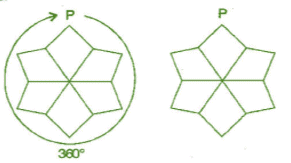
After rotating by 60o about a centre, a figure looks exactly the same as its original position. At what other angles will this happen for the figure?
Answer 6:
Other angles will be 120°, 180°,240°,300°,360°.
For 60° rotation:
It will rotate six times.
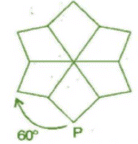
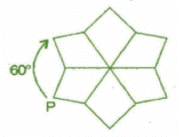
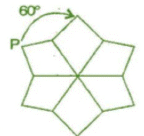
For 120° rotation:
It will rotate three times.
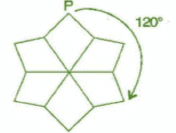
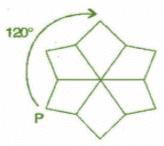
For 180° rotation:
It will rotate two times.

For 360° rotation:
It will rotate one time.
Question 7:
Can we have a rotational symmetry of order more than 1 whose angle of rotation is:
(i) 45o
(ii) 17o ?
Answer 7:
(i) If tiie angle of rotation is 45°, then symmetry of order is possible and would be 8 rotations.
(ii) If the angle of rotational is 17°, then symmetry o f order is not possible because 360° is not complete divided by 17°.
|
276 docs|155 tests
|
FAQs on NCERT Solutions for Class 8 Maths - Symmetry- 2
| 1. What is symmetry? |  |
| 2. How is symmetry useful in daily life? |  |
| 3. What are the different types of symmetry? |  |
| 4. How can symmetry be identified in geometric shapes? |  |
| 5. Can all objects have symmetry? |  |

















