NCERT Solutions for Class 9 Maths Chapter 14 - Chapter 14 (Part -2) - Statistics,
Question 3:
Given below are the seats won by different political parties in the polling outcome of a state assembly elections:
| Political Party | A | B | C | D | E | F |
| Seats Won | 75 | 55 | 37 | 29 | 10 | 37 |
(i) Draw a bar graph to represent the polling results.
(ii) Which political party won the maximum number of seats?
Answer 3:
(i) By taking polling results on x-axis and seats won as y-axis and choosing an appropriate scale (1 unit = 10 seats for y-axis), the required graph of the above information can be constructed as follows.

Here, the rectangle bars are of the same length and have equal spacing in between them.
(ii) Political party ‘A’ won maximum number of seats.
Question 4:
The length of 40 leaves of a plant are measured correct to one millimetre, and the obtained data is represented in the following table
| Length (in mm) | Number of leaves |
| 118 − 126 | 3 |
| 127 − 135 | 5 |
| 136 − 144 | 9 |
| 145 − 153 | 12 |
| 154 − 162 | 5 |
| 163 − 171 | 4 |
| 172 − 180 | 2 |
(i) Draw a histogram to represent the given data.
(ii) Is there any other suitable graphical representation for the same data?
(iii) Is it correct to conclude that the maximum number of leaves are 153 mm long? Why?
Answer 4:
(i) It can be observed that the length of leaves is represented in a discontinuous class interval having a difference of 1 in between them. Therefore,(1/2 =0.5) has to be added to each upper class limit and also have to subtract 0.5 from the lower class limits so as to make the class intervals continuous.
| Length (in mm) | Number of leaves |
| 117.5 − 126.5 | 2 |
| 126.5 − 135.5 | 5 |
| 135.5 − 144.5 | 9 |
| 144.5 − 153.5 | 12 |
| 153.5 − 162.5 | 5 |
| 162.5 − 171.5 | 4 |
| 171.5 − 180.5 | 2 |

Taking the length of leaves on x-axis and the number of leaves on y-axis, the histogram of this information can be drawn as above.
Here, 1 unit on y-axis represents 2 leaves.
(ii) Other suitable graphical representation of this data is frequency polygon.
(iii) No, as maximum number of leaves (i.e., 12) has their length in between 144.5 mm and 153.5 mm. It is not necessary that all have their lengths as 153 mm.
Question 5:
The following table gives the life times of neon lamps:
| Length (in hours) | Number of lamps |
| 300 − 400 | 14 |
| 400 − 500 | 56 |
| 500 − 600 | 60 |
| 600 − 700 | 86 |
| 700 − 800 | 74 |
| 800 − 900 | 62 |
| 900 − 1000 | 48 |
(i) Represent the given information with the help of a histogram.
(ii) How many lamps have a lifetime of more than 700 hours?
Answer 5:
(i) By taking life time (in hours) of neon lamps on x-axis and the number of lamps on y-axis, the histogram of the given information can be drawn as follows.

Here, 1 unit on y-axis represents 10 lamps.
(ii) It can be concluded that the number of neon lamps having their lifetime more than 700 is the sum of the number of neon lamps having their lifetime as 700 − 800, 800 − 900, and 900 − 1000.
Therefore, the number of neon lamps having their lifetime more than 700 hours is 184. (74 + 62 + 48 = 184)
Question 6:
The following table gives the distribution of students of two sections according to the mark obtained by them:
| Section A | Section B | ||
| Marks | Frequency | Marks | Frequency |
| 0 − 10 | 3 | 0 − 10 | 5 |
| 10 − 20 | 9 | 10 − 20 | 19 |
| 20 − 30 | 17 | 20 − 30 | 15 |
| 30 − 40 | 12 | 30 − 40 | 10 |
| 40 − 50 | 9 | 40 − 50 | 1 |
Represent the marks of the students of both the sections on the same graph by two frequency polygons. From the two polygons compare the performance of the two sections.
Answer 6:
We can find the class marks of the given class intervals by using the following formula.

| Section A | Section B | ||||
| Marks | Class marks | Frequency | Marks | Class marks | Frequency |
| 0 − 10 | 5 | 3 | 0 − 10 | 5 | 5 |
| 10 − 20 | 15 | 9 | 10 − 20 | 15 | 19 |
| 20 − 30 | 25 | 17 | 20 − 30 | 25 | 15 |
| 30 − 40 | 35 | 12 | 30 − 40 | 35 | 10 |
| 40 − 50 | 45 | 9 | 40 − 50 | 45 | 1 |
Taking class marks on x-axis and frequency on y-axis and choosing an appropriate scale (1 unit = 3 for y-axis), the frequency polygon can be drawn as follows.

It can be observed that the performance of students of section ‘A’ is better than the students of section ‘B’ in terms of good marks.
Question 7:
The runs scored by two teams A and B on the first 60 balls in a cricket match are given below:
| Number of balls | Team A | Team B |
| 1 − 6 | 2 | 5 |
| 7 − 12 | 1 | 6 |
| 13 − 18 | 8 | 2 |
| 19 − 24 | 9 | 10 |
| 25 − 30 | 4 | 5 |
| 31 − 36 | 5 | 6 |
| 37 − 42 | 6 | 3 |
| 43 − 48 | 10 | 4 |
| 49 − 54 | 6 | 8 |
| 55 − 60 | 2 | 10 |
Represent the data of both the teams on the same graph by frequency polygons.
[Hint: First make the class intervals continuous.]
Answer 7:
It can be observed that the class intervals of the given data are not continuous. There is a gap of 1 in between them. Therefore, (1/2 = 0.5) has to be added to the upper class limits and 0.5 has to be subtracted from the lower class limits.
Also, class mark of each interval can be found by using the following formula.

Continuous data with class mark of each class interval can be represented as follows.
| Number of balls | Class mark | Team A | Team B |
| 0.5 − 6.5 | 3.5 | 2 | 5 |
| 6.5 − 12.5 | 9.5 | 1 | 6 |
| 12.5 − 18.5 | 15.5 | 8 | 2 |
| 18.5 − 24.5 | 21.5 | 9 | 10 |
| 24.5 − 30.5 | 27.5 | 4 | 5 |
| 30.5 − 36.5 | 33.5 | 5 | 6 |
| 36.5 − 42.5 | 39.5 | 6 | 3 |
| 42.5 − 48.5 | 45.5 | 10 | 4 |
| 48.5 − 54.5 | 51.5 | 6 | 8 |
| 54.5 − 60.5 | 57.5 | 2 | 10 |
By taking class marks on x-axis and runs scored on y-axis, a frequency polygon can be constructed as follows.

Question 8:
A random survey of the number of children of various age groups playing in park was found as follows:
| Age (in years) | Number of children |
| 1 − 2 | 5 |
| 2 − 3 | 3 |
| 3 − 5 | 6 |
| 5 − 7 | 12 |
| 7 − 10 | 9 |
| 10 − 15 | 10 |
| 15 − 17 | 4 |
Draw a histogram to represent the data above.
Answer 8:
Here, it can be observed that the data has class intervals of varying width. The proportion of children per 1 year interval can be calculated as follows.
| Age (in years) | Frequency (Number of children) | Width of class | Length of rectangle |
| 1 − 2 | 5 | 1 |  |
| 2 − 3 | 3 | 1 |  |
| 3 − 5 | 6 | 2 |  |
| 5 − 7 | 12 | 2 |  |
| 7 − 10 | 9 | 3 |  |
| 10 − 15 | 10 | 5 |  |
| 15 − 17 | 4 | 2 |  |
Taking the age of children on x-axis and proportion of children per 1 year interval on y-axis, the histogram can be drawn as follows.

Question 9:
100 surnames were randomly picked up from a local telephone directory and a frequency distribution of the number of letters in the English alphabet in the surnames was found as follows:
| Number of letters | Number of surnames |
| 1 − 4 | 6 |
| 4 − 6 | 30 |
| 6 − 8 | 44 |
| 8 − 12 | 16 |
| 12 − 20 | 2 |
(i) Draw a histogram to depict the given information.
(ii) Write the class interval in which the maximum number of surname lie.
Answer 9:
(i) Here, it can be observed that the data has class intervals of varying width. The proportion of the number of surnames per 2 letters interval can be calculated as follows.
| Number of letters | Frequency (Number of surnames) | Width of class | Length of rectangle |
| 1 − 4 | 6 | 3 |  |
| 4 − 6 | 30 | 2 |  |
| 6 − 8 | 44 | 2 |  |
| 8 − 12 | 16 | 4 |  |
| 12 − 20 | 4 | 8 |  |
By taking the number of letters on x-axis and the proportion of the number of surnames per 2 letters interval on y-axis and choosing an appropriate scale (1 unit = 4 students for y axis), the histogram can be constructed as follows.

(ii) The class interval in which the maximum number of surnames lies is 6 − 8 as it has 44 surnames in it i.e., the maximum for this data.
The number of goals scored by the team is
2, 3, 4, 5, 0, 1, 3, 3, 4, 3

= 28/10 = 2.8
= 2.8 goals
Arranging the number of goals in ascending order,
0, 1, 2, 3, 3, 3, 3, 4, 4, 5
The number of observations is 10, which is an even number. Therefore, median score will be the mean of 10/2 i.e., 5th and (10/2 +1) i.e., 6th observation while arranged in ascending or descending order.

= (3+3/2)
= (6/2)
= 3
Mode of data is the observation with the maximum frequency in data.
Therefore, the mode score of data is 3 as it has the maximum frequency as 4 in the data.
Question 2:
In a mathematics test given to 15 students, the following marks (out of 100) are recorded:
41, 39, 48, 52, 46, 62, 54, 40, 96, 52, 98, 40, 42, 52, 60
Find the mean, median and mode of this data.
Answer 2:
The marks of 15 students in mathematics test are
41, 39, 48, 52, 46, 62, 54, 40, 96, 52, 98, 40, 42, 52, 60


= 822/15= 54.8
Arranging the scores obtained by 15 students in an ascending order,
39, 40, 40, 41, 42, 46, 48, 52, 52, 52, 54, 60, 62, 96, 98
As the number of observations is 15 which is odd, therefore, the median of data will be (15+1)/2= 8thobservation whether the data is arranged in an ascending or descending order.
Therefore, median score of data = 52
Mode of data is the observation with the maximum frequency in data. Therefore, mode of this data is 52 having the highest frequency in data as 3.
Question 3:
The following observations have been arranged in ascending order. If the median of the data is 63, find the value of x.
29, 32, 48, 50, x, x + 2, 72, 78, 84, 95
Answer 3:
It can be observed that the total number of observations in the given data is 10 (even number). Therefore, the median of this data will be the mean of 10/2 i.e., 5th and 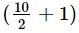 i.e., 6th observation.
i.e., 6th observation.

⇒ 63 = 
⇒ 63 = 
⇒ 63 x+1
⇒ x = 62
Question 4:
Find the mode of 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18.
Answer 4:
Arranging the data in an ascending order,
14, 14, 14, 14, 17, 18, 18, 18, 22, 23, 25, 28
It can be observed that 14 has the highest frequency, i.e. 4, in the given data. Therefore, mode of the given data is 14.
Question 5:
Find the mean salary of 60 workers of a factory from the following table:
| Salary (in Rs) | Number of workers |
| 3000 | 16 |
| 4000 | 12 |
| 5000 | 10 |
| 6000 | 8 |
| 7000 | 6 |
| 8000 | 4 |
| 9000 | 3 |
| 1000 | 2 |
| Total | 1 |
Answer 5:
We know that


| Salary (in Rs) (xi) | Number of workers (fi) | fixi |
| 3000 | 16 | 3000 × 16 = 48000 |
| 4000 | 12 | 4000 × 12 = 48000 |
| 5000 | 10 | 5000 × 10 = 50000 |
| 6000 | 8 | 6000 × 8 = 48000 |
| 7000 | 6 | 7000 × 6 = 42000 |
| 8000 | 4 | 8000 × 4 = 32000 |
| 9000 | 3 | 9000 × 3 = 27000 |
| 10000 | 1 | 10000 × 1 = 10000 |
| Total |  |  |

= 5083.33
Therefore, mean salary of 60 workers is Rs 5083.33.
Question 6:
Give one example of a situation in which
(i) The mean is an appropriate measure of central tendency.
(ii) The mean is not an appropriate measure of central tendency but the median is an appropriate measure of central tendency.
Answer 6:
When any data has a few observations such that these are very far from the other observations in it, it is better to calculate the median than the mean of the data as median gives a better estimate of average in this case.
(i) Consider the following example − the following data represents the heights of the members of a family.
154.9 cm, 162.8 cm, 170.6 cm, 158.8 cm, 163.3 cm, 166.8 cm, 160.2 cm
In this case, it can be observed that the observations in the given data are close to each other. Therefore, mean will be calculated as an appropriate measure of central tendency.
(ii) The following data represents the marks obtained by 12 students in a test.
48, 59, 46, 52, 54, 46, 97, 42, 49, 58, 60, 99
In this case, it can be observed that there are some observations which are very far from other observations. Therefore, here, median will be calculated as an appropriate measure of central tendency.
|
1 videos|228 docs|21 tests
|
FAQs on NCERT Solutions for Class 9 Maths Chapter 14 - Chapter 14 (Part -2) - Statistics,
| 1. What are the measures of central tendency in statistics? |  |
| 2. How is the mean calculated in statistics? |  |
| 3. What is the difference between the mean and median in statistics? |  |
| 4. How is the mode calculated in statistics? |  |
| 5. How can statistics be used in real life? |  |

|
Explore Courses for Class 9 exam
|

|


















