NCERT Solutions for Class 9 - Maths Circles Exercise 9.3
Q1. In Fig, A, B and C are three points on a circle with centre O such that ∠ BOC = 30° and ∠ AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.
Ans: It is given that,
∠AOC = ∠AOB+∠BOC
So, ∠AOC = 60°+30°
∴ ∠AOC = 90°
It is known that an angle which is subtended by an arc at the centre of the circle is double the angle subtended by that arc at any point on the remaining part of the circle.
So,
∠ADC = (½)∠AOC
= (½)× 90° = 45°
Q2. A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Ans:
Let O be the center of the circle, and AB be the chord such that AB=r, where r is the radius of the circle.
Since AB=r, OAB forms an equilateral triangle (because all sides OA,OB, and AB are equal to the radius).In an equilateral triangle, all angles are 60∘. Hence, the angle subtended by the chord AB at the center O is:
∠AOB=60∘
By the property of a circle, the angle subtended by a chord at the circumference is half the angle subtended at the center. Hence, the angle subtended by the chord AB at a point on the minor arc is:
The angle subtended by the chord AB at a point on the major arc is the supplementary angle to the angle subtended on the minor arc (because the two angles together make 180∘). Hence:
Q3. In Fig, ∠ PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠ OPR.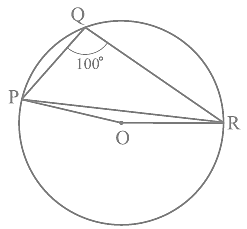
Ans: The angle which is subtended by an arc at the centre of the circle is double the angle subtended by that arc at any point on the remaining part of the circle.
So, the reflex ∠POR = 2×∠PQR
We know the values of angle PQR as 100°
So, ∠POR = 2×100° = 200°
∴ ∠POR = 360°-200° = 160°
Now, in ΔOPR,
OP and OR are the radii of the circle
So, OP = OR
Also, ∠OPR = ∠ORP
Now, we know the sum of the angles in a triangle is equal to 180 degrees
So,
∠POR+∠OPR+∠ORP = 180°
∠OPR+∠OPR = 180°-160°
As ∠OPR = ∠ORP
2∠OPR = 20°
Thus, ∠OPR = 10°
Q4. In Fig, ∠ ABC = 69°, ∠ ACB = 31°, find ∠ BDC.
Ans: We know that angles in the segment of the circle are equal so,
∠BAC = ∠BDC
Now in the in ΔABC, the sum of all the interior angles will be 180°
So, ∠ABC + ∠BAC + ∠ACB = 180°
Now, by putting the values,
∠BAC = 180° - 69° - 31°
So, ∠BAC = 80°
∴ ∠BDC = 80°.
Q5. In Fig, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠ BEC = 130° and ∠ ECD = 20°. Find ∠ BAC.
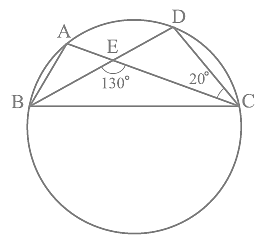
Ans: We know that the angles in the segment of the circle are equal.
So,
∠ BAC = ∠ CDE
Now, by using the exterior angles property of the triangle
In ΔCDE we get,
∠ CEB = ∠ CDE + ∠ DCE
We know that ∠ DCE is equal to 20°
So, ∠ CDE = 110°
∠ BAC and ∠ CDE are equal
∴ ∠ BAC = 110°.
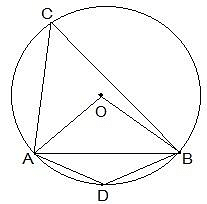
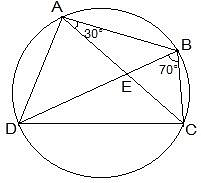
Q6. ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠ DBC = 70°, ∠ BAC is 30°, find ∠ BCD. Further, if AB = BC, find ∠ ECD.
Ans: Consider the following diagram.Consider the chord CD,
We know that angles in the same segment are equal.
So, ∠ CBD = ∠ CAD
∴ ∠ CAD = 70°
Now, ∠ BAD will be equal to the sum of angles BAC and CAD.
So, ∠ BAD = ∠ BAC + ∠ CAD
= 30° + 70°
∴ ∠ BAD = 100°
We know that the opposite angles of a cyclic quadrilateral sums up to 180 degrees.
So,
∠ BCD + ∠ BAD = 180°
It is known that ∠ BAD = 100°
So, ∠ BCD = 80°
Now consider the ΔABC.
Here, it is given that AB = BC
Also, ∠ BCA = ∠ CAB (They are the angles opposite to equal sides of a triangle)
∠ BCA = 30°
also, ∠ BCD = 80°
∠ BCA + ∠ ACD = 80°
Thus, ∠ ACD = 50° and ∠ ECD = 50°.
Q7. If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Ans: Given:
1. The diagonals of the cyclic quadrilateral are diameters of the circle.
2. The quadrilateral is cyclic (its vertices lie on the circle).
Proof:
A diameter of a circle subtends a 90∘ angle on the circumference of the circle (by the property of a semicircle).
Let the cyclic quadrilateral be ABCD, and let the diagonals AC and BD be the diameters of the circle.
Since AC is a diameter:
∠ABC=90∘ and ∠ADC=90∘(Both ∠ABC and ∠ADC are subtended by AC on opposite sides of the circle).
Similarly, since BD is a diameter:
∠BAD = 90∘ and ∠BCD = 90∘ (Both ∠BAD and ∠BCD are subtended by BD).
From the above, all four angles of the quadrilateral ABCD are 90∘. Hence, ABCD is a quadrilateral where:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90∘
Q8. If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Ans: Construction:
Consider a trapezium ABCD with AB ║CD and BC = AD.
Draw AM ⊥ CD and BN ⊥ CD.
In ΔAMD and ΔBNC,
The diagram will look as follows:In ΔAMD and ΔBNC,
AD = BC (Given)
∠AMD = ∠BCN (By construction, each is 90º)
AM = BN (Perpendicular distance between two parallel lines is same)
ΔAMD, ΔBNC (RHS congruence rule)
∠ADC = ∠BCD (CPCT)...(1)
∠BAD and ∠ADC = 180º....(2)
∠BAD and ∠BCD = 180º [Using equation (1)]
This equation shows that the opposite angle are supplementary.
Therefore, ABCD is a cyclic quadrilateral.
Q9. Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig). Prove that ∠ACP = ∠ QCD.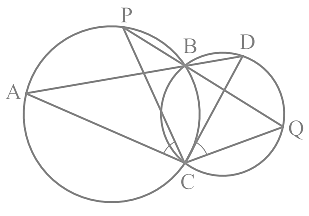
Ans: Construction:
Join the chords AP and DQ.
For chord AP, we know that angles in the same segment are equal.
So, ∠ PBA = ∠ ACP ......(i)
Similarly for chord DQ,
∠ DBQ = ∠ QCD .....(ii)
It is known that ABD and PBQ are two line segments which are intersecting at B.
At B, the vertically opposite angles will be equal.
∴ ∠ PBA = ∠ DBQ ......(iii)
From equation (i), equation (ii) and equation (iii) we get,
∠ ACP = ∠ QCD.
Q10. If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Ans: First draw a triangle ABC and then two circles having diameter as AB and AC respectively.
We will have to now prove that D lies on BC and BDC is a straight line.Proof:
We know that angle in the semi-circle are equal
So, ∠ ADB = ∠ ADC = 90°
Hence, ∠ ADB + ∠ ADC = 180°
∴ ∠ BDC is straight line.
So, it can be said that D lies on the line BC.
Q11. ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Ans: We know that AC is the common hypotenuse and ∠ B = ∠ D = 90°.
Now, it has to be proven that ∠ CAD = ∠ CBDSince, ∠ ABC and ∠ ADC are 90°, it can be said that They lie in the semi-circle.
So, triangles ABC and ADC are in the semi-circle and the points A, B, C and D are concyclic.
Hence, CD is the chord of the circle with center O.
We know that the angles which are in the same segment of the circle are equal.
∴ ∠ CAD = ∠ CBD
Q12. Prove that a cyclic parallelogram is a rectangle.
Ans: It is given that ABCD is a cyclic parallelogram and we will have to prove that ABCD is a rectangle.
Proof:
Let ABCD be a cyclic parallelogram.
∠A + ∠C = 180º (Opposite angles of a cyclic quadrilateral)....(1)
We know that opposite angles of a parallelogram are equal.
∠A = ∠C and ∠B = ∠D
From equation (1),
∠A + ∠C = 180º
∠A + ∠A = 180º
2∠A = 180º
Parallelogram ABCD has one of its interior angles as 90º.
Thus, ABCD is a rectangle.
|
44 videos|412 docs|54 tests
|
FAQs on NCERT Solutions for Class 9 - Maths Circles Exercise 9.3
| 1. What is the general equation of a circle and how can it be derived? |  |
| 2. How do you find the radius of a circle when given its equation? |  |
| 3. What is the significance of the center of a circle in geometry? |  |
| 4. How can you determine if a point lies inside, on, or outside a circle? |  |
| 5. Can you explain how to solve problems involving the tangents of a circle? |  |

|
Explore Courses for Class 9 exam
|

|


 Consider the chord CD,
Consider the chord CD,
 In ΔAMD and ΔBNC,
In ΔAMD and ΔBNC,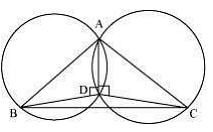 Proof:
Proof: Since, ∠ ABC and ∠ ADC are 90°, it can be said that They lie in the semi-circle.
Since, ∠ ABC and ∠ ADC are 90°, it can be said that They lie in the semi-circle.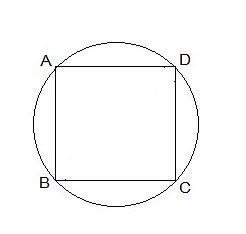 Proof:
Proof:

















