Necessary and Sufficient Conditions for Extrema - CSIR-NET Mathematical Sciences | Mathematics for IIT JAM, GATE, CSIR NET, UGC NET PDF Download
1 The second variation
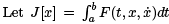 be a nonlinear functional, with x(a) = A and x(b) = B fixed. As usual, we will assume that F is as smooth as necessary.
be a nonlinear functional, with x(a) = A and x(b) = B fixed. As usual, we will assume that F is as smooth as necessary.
The first variation of J is
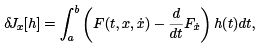
where h(t) is assumed as smooth as necessary and in addition satisfies h(a) = h(b) = 0. We will call such h admissible.
The idea behind finding the first variation is to capture the linear part of the J [x]. Specifically, we have
J[x + εh] = J [x] + εδJx[h] + o(ε),
where o(ε) is a quantity that satisfies
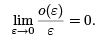
The second variation comes out of the quadratic approximation in ε,
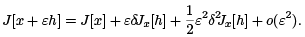
It follows that
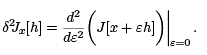
To calculate it, we note that
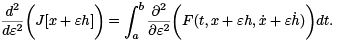
Applying the chain rule to the integrand, we see that
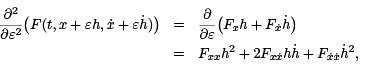
where the various derivatives of F are evaluated at 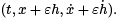 Setting ε = 0 and inserting the result in our earlier expression for the second variation, we obtain
Setting ε = 0 and inserting the result in our earlier expression for the second variation, we obtain
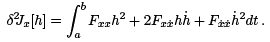
Note that the middle term can be written as 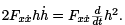 Using this in the equation above, integrating by parts, and employing h(a) = h(b) = 0, we arrive at
Using this in the equation above, integrating by parts, and employing h(a) = h(b) = 0, we arrive at
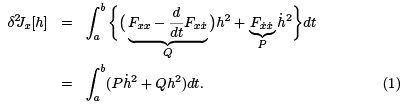
2 Legendre’s trick
Ultimately, we are interested in whether a given extremal for J is a weak (relative) minimum or maximum. In the sequel we will always assume that the function x(t) that we are working with is an extremal, so that x(t) satisfies the Euler-Lagrange equation, 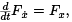 makes the first variation δJx[h] = 0 for all h, and fixes the functions
makes the first variation δJx[h] = 0 for all h, and fixes the functions 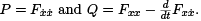
To be definite, we will always assume we are looking for conditions for the extremum to be a weak minimum. The case of a maximum is similar.
Let’s look at the integrand  It is generally true that a function can be bounded, but have a derivative that varies wildly. Our intuition then says that
It is generally true that a function can be bounded, but have a derivative that varies wildly. Our intuition then says that 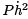 is the dominant term, and this turns out to be true. In looking for a minimum, we recall that it is necessary that δ2Jx [h] ≥ 0 for all h. One can use this to show that, for a minimum, it is also necessary, but not sufficient, that P ≥ 0 on [a, b]. We will make the stronger assumption that P > 0 on [a, b]. We also assume that P and Q are smooth.
is the dominant term, and this turns out to be true. In looking for a minimum, we recall that it is necessary that δ2Jx [h] ≥ 0 for all h. One can use this to show that, for a minimum, it is also necessary, but not sufficient, that P ≥ 0 on [a, b]. We will make the stronger assumption that P > 0 on [a, b]. We also assume that P and Q are smooth.
Legendre had the idea to add a term to δ2J to make it nonnegative. Specifically, he added 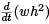 to the integrand in (1). Note that
to the integrand in (1). Note that 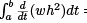
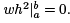 Hence, we have this chain of equations,
Hence, we have this chain of equations,
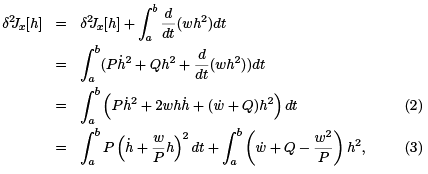
where we completed the square to get the last equation. If we can find w(t) such that

then the second variation becomes
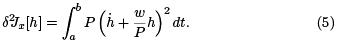
Equation (4) is called a Riccati equation. It can be turned into the second order linear ODE below via the substitution 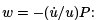
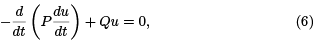
which is called the Jacobi equation for J . Two points t = α and 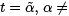
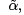 are said to be conjugate points for Jacobi’s equation if there is a solution u to (6) such that
are said to be conjugate points for Jacobi’s equation if there is a solution u to (6) such that 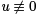 between α and
between α and 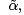 and such that
and such that 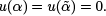
When there are no points conjugate to t = a in the interval [a, b], we can construct a solution to (6) that is strictly positive on [a, b]. Start with the two linearly indepemdent solutions u0 and u1 to (6) that satsify the initial conditions
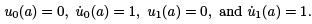
Since there is no point in [a, b] conjugate a, u0 (t) ≠ 0 for any a < t ≤ b. In particular, since u˙ 0 (a) = 1 > 0, u(t) will be strictly positive on (a, b]. Next, because u1(a) = 1, there exists t = c, a < c ≤ b, such that u1(t) ≥ 1/2 on [a, c]. Moreover, the continuity of u0 and u1 on [c, b] implies that minc≤t≤b u0(t) = m0 > 0 and minc≤t≤b u1(t) = m1 ∈ R. It is easy to check that on [a, b],
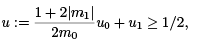
and, of course, u solves (6).
This means that the substitutuion  yields a solution to the Riccati equation (4), and so the second variation has the form given in (5).
yields a solution to the Riccati equation (4), and so the second variation has the form given in (5).
It follows that δ2Jx[h] ≥ 0 for any admissible h. Can the second variation vanish for some h that is nonzero? That is, can we find an admissible h ≡ 0 such that δ2Jx[h] = 0? If it did vanish, we would have to have
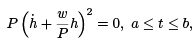
and, since P > 0, this implies that 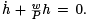 This first order linear equation has the unique solution,
This first order linear equation has the unique solution,
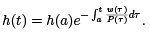
However, since h is admissible, h(a) = h(b) = 0, and so h(t) ≡ 0. We have proved the following result.
Proposition 2.1. If there are no points in [a, b] conjugate to t = a, the the second variation is a positive definite quadratic functional. That is, δ2Jx [h] > 0 for any admissible h not identical ly 0.
3 Conjugate points
There is direct connection between conjugate points and extremals. Let x(t, ε) be a family of extremals for the functional J depending smoothly on a parameter ε. We will assume that x(a, ε) = A, which will be independent of ε. These extremals all satisfy the Euler-Lagrange equation
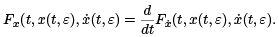
If we differentiate this equation with respect to ε, being careful to correctly apply the chain rule, we obtain
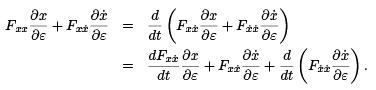
Cancelling and rearranging terms, we obtain
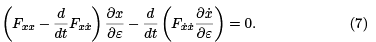
Set ε = 0 and let u(t)  Observe that the functions in the equation above, which is called the variational equation, are just
Observe that the functions in the equation above, which is called the variational equation, are just 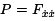 and Q =
and Q = 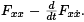
Consequently, (7) is simply the Jacobi equation (6). The difference here is that we always have the initial conditions,
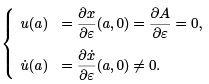
We remark that if u˙ (a) = 0, then u(t) ≡ 0.
What do conjugate points mean in this context? Suppose that 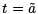 is conjugate to t = a. Then we have
is conjugate to t = a. Then we have
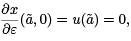
which holds independently of how our smooth family of extremals was constructed. It follows that at 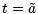 , we have
, we have 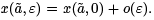 . Thus, the family either crosses again at
. Thus, the family either crosses again at 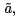 or comes close to it, accumulating to order higher than ε there.
or comes close to it, accumulating to order higher than ε there.
4 Sufficient conditions
A sufficient condition for an extremal to be a relative minimum is that the second variation be strongly positive definite. This means that there is a c > 0, which is independent of h, such that for all admissible h one has
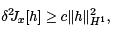
where H1 = H1[a, b] denotes the usual Sobolev space of functions with distributional derivatives in L2 [a, b].
Let us return to equation (2), where we added in terms depending on an arbitrary function w. In the integrand there, we will add and subtract 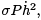 where σ is an arbitary constant. The only requirement for now is that 0 < σ < mint∈[a,b] P (t). The result is
where σ is an arbitary constant. The only requirement for now is that 0 < σ < mint∈[a,b] P (t). The result is
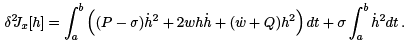
For the first integral in the term on the right above, we repeat the argument that was used to arrive at (5). Everything is the same, except that P is replaced by P − σ. We arrive at this:
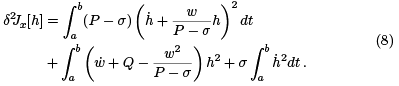
We continue as we did in section 2. In the end, we arrive at the new Jacobi equation,
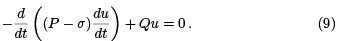
The point is that if for the Jacobi equation (6) there are no points in [a, b] conjugate to a, then, because the solutions are continuous functions of the parameter σ, we may choose σ small enough so that for (9) there will be no points conjugate to a in [a, b]. Once we have fouund σ small enough for this to be true, we fix it. We then solve the corresponding Riccati equation and employ it in (8) to obtain
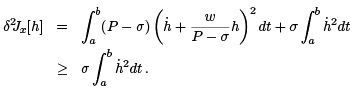
Now, for an admissble h, it is easy to show that 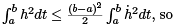 that we have
that we have
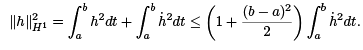
Consequently, we obtain this inequality:
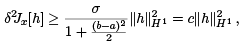
which is what we needed for a relative minimum. We summarize what we found below.
Theorem 4.1. A sufficient condition for an extremal x(t) to be a relative minimum for the functional 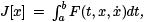 where x(a) = A and x(b) = B , is that P (t)
where x(a) = A and x(b) = B , is that P (t) 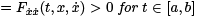 and that the interval [a, b] contain no points conjugate to t = a.
and that the interval [a, b] contain no points conjugate to t = a.
|
556 videos|198 docs
|
FAQs on Necessary and Sufficient Conditions for Extrema - CSIR-NET Mathematical Sciences - Mathematics for IIT JAM, GATE, CSIR NET, UGC NET
| 1. What are necessary conditions for extrema in mathematical optimization? |  |
| 2. What are sufficient conditions for extrema in mathematical optimization? |  |
| 3. How does the first-order derivative test determine extrema? |  |
| 4. What is the second-order derivative test in mathematical optimization? |  |
| 5. How does convexity/concavity affect extrema in mathematical optimization? |  |
|
556 videos|198 docs
|

|
Explore Courses for Mathematics exam
|

|

















