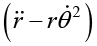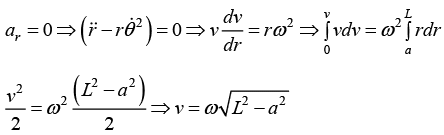Newton's Laws of Motion: Assignment | Mechanics & General Properties of Matter - Physics PDF Download
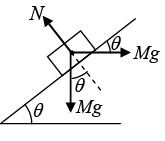
Q.1. Two touching bars 1 and 2 are placed on an inclined plane forming an angle α with the horizontal (Fig). The masses of the bars are equal to m1 and m2, and the coefficients of friction between the inclined plane and these bars are equal to k1 and k2 respectively, with k1 > k2. Find: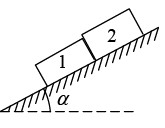 (a) the force of interaction of the bars in the process of motion;
(a) the force of interaction of the bars in the process of motion;
(b) the minimum value of the angle a at which the bars start sliding down.
(a) Pulling force F = m1g sin α + m2g sin α - k1m1g cos α k2m2g cos α
Then acceleration α is:…(i)
F.B.D of m1:
R is the reaction from the incline and N is the force of interaction between the blocks. Since m1 is sliding, frictional force on it is k1m1g cos α
m1g sin α + N - k1m1g cos α = m1α ...(ii)
(b) For minimum value of a acceleration will be zero and friction force will be at maximum value then⇒
Q.2. A particle of mass m during its motion in the plane xy according to the law x = a sin ωt, y = b cos ωt, where a, b and ω are constants.
(a) Find the velocity vector
(b) Find the magnitude and direction of the force acting on the particle
(c) Prove that angular motion of the system is conserve
(a)
whereposition vector of particle.
(c) Hence the force is central then angular momentum of system is conserve.
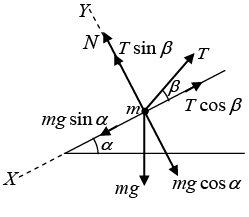
Q.3. A bar of mass m is pulled by means of a thread up an inclined plane forming an angle α with the horizontal (Figure).
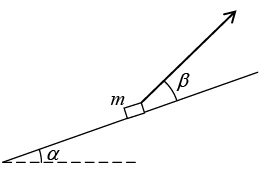 The coefficient of friction is equal to k. Find the angle β which the thread must form with the inclined plane for the tension of the thread to be minimum. What is it equal to?
The coefficient of friction is equal to k. Find the angle β which the thread must form with the inclined plane for the tension of the thread to be minimum. What is it equal to?
When block pull up. Direction of friction will be downward.
F.B.D. of block:
N = mg cos α - T sin β
fr = k (mg cos α - T sin β)
At just sliding:
T cos β = mg sin α + k(mg cos α - T sin β)
For the minimum value of T, cos β + k sin β should be maximum.
Let f (β) = (cos β + k sin β)
Now, for equilibrium point
∂f(β)/∂β = 0 ⇒ sin β + k cos β = 0 ⇒ tan β = k
Hence maximum value of f (b)
Q.4. In planar polar co-ordinates, an object’s position at time t is given as
(r, θ) = (etm, √8t rad)
(a) Find radial velocity tangential velocity and speed of particle at t = 0
(b) Find radial acceleration tangential acceleration and magnitude of acceleration at t = 0
(r, θ) = (etm, √8t rad)
Speed of particle is given by= √9 = 3m/sec
(b) Magnitude of acceleration- 8 x et at t = 0, 1 - 8 x 1 = -7m/sec2
Magnitude of acceleration is
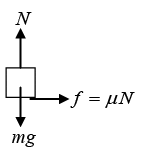
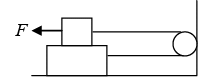
Q.5. The coefficient of static friction between the two blocks of M of 6 kg and m of 2 kg as shown in figure, is 0.2 and table is smooth. Then maximum horizontal force F that can be applied to the block of mass M so that the two blocks move together.
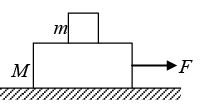
It is given M = 6kg m = 2kg.
For the two blocks to move together there acceleration should be equal. Let the acceleration of ( M + m ) be a . Then
Using Newton’s law for mass m
f = ma = 2F/8 = F/4
Now f ≤ μN∴ F/4 ≤ 0.2 x 2 x 10 ⇒ F/4 ≤ 4 N ⇒ F ≤ 16 N
Q.6. A particle P of mass m is constrained to move on the surface of cylinder under a force 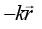 as shown in figure (k is the positive constant). Which of the following statements is/are correct? (Neglect friction.)
as shown in figure (k is the positive constant). Which of the following statements is/are correct? (Neglect friction.)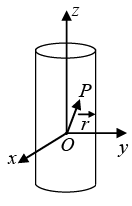 (a) Prove that the force is conservative.
(a) Prove that the force is conservative.
(b) Write the equation of motion along 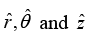
(c) Prove that motion along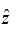 is oscillatory with frequency
is oscillatory with frequency 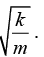
(d) Prove that angular momentum of the particle about O is conserved.
(e) Write down expression of the total energy.
(a)
(b) Fr = -kr, Fz = -kz Fθ = 0 so angular momentum conserve
(c) Fz = -kz ⇒= -kz the motion along z is simple harmonic motion with angular
frequency
(d) Fθ = 0, so angular momentum is conserved
(e) The total energy is given by
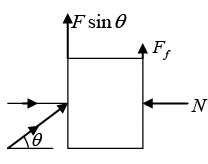
Q.7. A book of mass M is positioned against a vertical wall. The coefficient of friction between the book and the wall is μ. You wish to keep the book from falling by pushing on it with a force F applied at an angle θ with respect to the horizontal (-π/2 < θ < π/2), as shown in figure.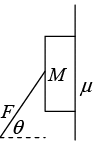 (a) For a given θ, what is the minimum F required.
(a) For a given θ, what is the minimum F required.
(b) For what θ is this minimum F the smallest? What is the corresponding minimum F?
(c) What is the limiting value of θ, below which there does not exist an F that keeps the book up?
(a) The normal force from the wall is F cos θ, so the friction force Ff holding the book up is at most μF cos θ. Gravitational force, which is Mg , and the vertical component of F , which is F sin θ. If the book is to stay at rest, we must have F sin θ + Ff - Mg = 0.
F (sin θ + μ cos θ) ≥ Mg .
Therefore, F must satisfy
assuming that sin θ + μ cos θ is positive. If it is negative then there is no solution for F .
(b) To minimize this lower bound, we must maximize the denominator. Talking the derivative gives cos θ - μ sin θ = 0 ⇒ tan θ = 1/μ. Plugging this value of θ back intoEquation, gives
This is the smallest possible F that keeps the book up, and the angle must be θ = tan-1 (1-μ) for it work. We see that if μ is very small, then to minimize your F , you should push essentially vertically with a force m mg . But if μ is very large, you should push essentially horizontally with a force mg/μ.
(c) There is no possible F that satisfies the condition (if the right-hand side is infinite if the coefficient of F is zero or negative). This occurs when
tan θ = - μ
If θ is more negative than this, then it is impossible to keep the book up, no matter how hard you push.
Q.8. A projectile is fired from the origin O at an angle of 45º from the horizontal as shown in figure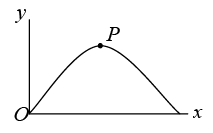 (a) Find the maximum height and range of projectile
(a) Find the maximum height and range of projectile
(b) At the highest point P of its trajectory find the radial and transverse components of its acceleration in terms of the gravitational acceleration g.
(a) Maximum hmax
where θ = π/4
(b)
From the figure αr = g cos (90 - α) = - g sin α = -g/√5
αθ = - g cos α = -2g/√5
Q.9. A block of mass M rests on a fixed plane inclined at an angle θ. You apply a horizontal force of Mg on the block, as shown in figure. Assume that the friction force between the block and the plane is large enough to keep the block at rest.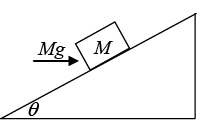 (a) What are the normal and friction forces (call them N and Ff) that the plane exerts on the block?
(a) What are the normal and friction forces (call them N and Ff) that the plane exerts on the block?
(b) If the coefficient of static friction is μ, for what range of angles θ will the block in fact remain at rest?
(a) The free body diagram of the block is shown below: The normal force on the block can be calculated using Newton’s second law in the direction perpendicular to the incline.
N - Mg cos θ - Mg sin θ = 0
⇒ N = Mg (sin θ + cos θ)
Maximum value of static frictional force
fs = μMg(sin θ + cos θ)
(b) The coefficient m tells us that |Ff| ≤ μN. Using Eq this inequality becomes
Mg |sin θ - cos θ| ≤ μMg(cos θ + sin θ) ....(1)
The absolute value here signifies that we must consider two cases:
If tan θ ≥ 1, then Eq. (1) becomes
sin θ cos θ ≤ μ(cos θ + sinθ) ⇒ tan θ ≤ 1 + μ/1 - μ.
Q.10. A bead moves along the spoke of a wheel at constant speed u meters per second. The wheel rotates with uniform angular velocity  = ω radians per second about an axis fixed in space. At t = 0, the spoke is along the x-axis and the bead is at the origin.
= ω radians per second about an axis fixed in space. At t = 0, the spoke is along the x-axis and the bead is at the origin.
(a) Find the velocity at time t in polar coordinates
(b) Find the velocity at time t in Cartesian coordinates
(c) Find the acceleration at time t in polar coordinates
(a)
Hence
To specify the velocity completely, we need to know the direction ofThis is obtained from r = (r,θ) = (ut, ωt).
(b) In Cartesian coordinates, we have vx = vr cosθ - vθ cos θ - vθ sin θ and vy = vr + cos θ + vθ cos θ
Since vr = u, vθ = rω = utω, θ = ωt, we obtain
v = (u cos ωt - utω sinωt)+ (u sin ωt - utω cos ωt)
Note how much simpler the result is in plane polar coordinates.
(c) The acceleration is α =
Q.11. Find the acceleration w of body 2 in the arrangement shown in figure, if its mass is η times as great as the mass of 1 and the angle that the inclined plane forms with the horizontal is equal to α. The masses of the pulley and threads, as well as the friction, are assumed to be negligible.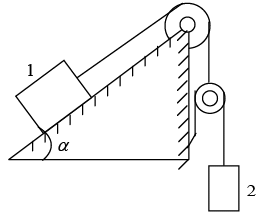
Let acceleration of mass 1 is α1 and acceleration of mass 2 is α2. If mass 1 moves x distance then mass 2 moves 2x distance then 2α1 = α2.
Let α2 = α then α1 = α/2
Force on mass 1:
Using Newton’s second law to the pulley gives T1 = 2T2
Let T1 = T then T2 = T/2
Motion of body (1): T - mg sin α = m(α/2) ...(i)
The force on pulley and mass 2:
Motion of body (2): ηmg - T/2 = ηma ⇒ 2η mg - T = 2η mα ...(ii)
from (i) and (ii):
Q.12. A mass hangs from a massless string of length of l. Conditions have been set up so that the mass swings around in a horizontal circle, with the string making a constant angle β with the vertical (see figure). What is the angular frequency, w, of this motion?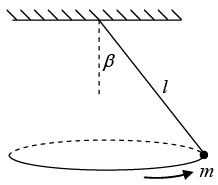
The mass travels in a circle, so the horizontal radial force must be Fr =
≡ mrω2 (with r = ℓ sin β), directed radially inward. The forces on the mass are the tension in the string, T , and gravity, mg (see figure). There is no acceleration in the vertical direction, so F = mα in the vertical and radial directions give, respectively,
T cos β - mg = 0,
T sin β = m(ℓ sin β)ω2.Solving for ω gives
If β ≈ 90º, then ω ⇢ ∞, which makes sense. And if β ≈ 0, then ω ≈which happens to equal the frequency of a plane pendulum of length ℓ.
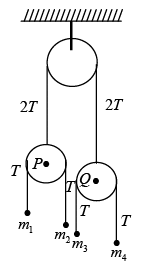
Q.13. Find the acceleration of the blocks as shown in figure.
If m1 = 1kg , m2 = 2kg , m3 = 0.5, m4 = 4kg , take g = 10 m/s2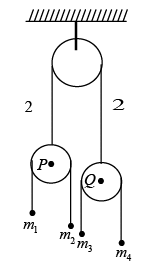
Let a1, a2, a3 and a4 be the downward accelerations of
m1, m2, m3 and m4 respectively.
From Newton’s second law the on masses:1g - T = 1α1 ....(i)
2 g - T= 2α2 .... (ii)
0.5g - T = 0.5α3 ...(iii)
4g - T = 4α4 ...(iv)
From equation of constrain
a1 + a2 + a3 + a4 = 0
Where a1 + a2 + a3 + a4 are downward acceleration of respective masses.
Solving these five equations, we get:down
down.
Q.14. A mass, which is free to move on a horizontal frictionless surface, is attached to one end of a massless string that wraps partially around a frictionless vertical pole of radius a (see the top view in figure).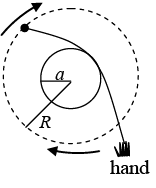
You hold on to the other end of the string. At t = 0, the mass has speed v0 in the tangential direction along the dotted circle of radius R shown. Your task is to pull on the string so that the mass keeps moving along the dotted circle. You are required to do this in such a way that the string remains in contact with the pole at all times. (You will have to move your hand around the pole, of course). What is the speed of the mass as a function time?
Let F be the string. At the mass, the angle between the string and the radius of the dotted circle is θ = sin-1 (α/R). In terms of θ,
the radial and tangential F = mα equations are
For circular motion
For circular motionDividing these two equations gives tan θ = dv/dt R/v2. Separating variables and integrating gives
The speed v becomes infinite when
This means that you can keep the mass moving in the desired circle only up to time T . After that, it is impossible, for all practical purpose, long before v becomes infinite). The total distance
d = ∫vdt, is infinite because this integral diverges(barely, like a log) as t approaches T.
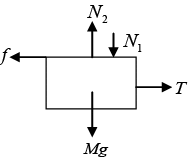
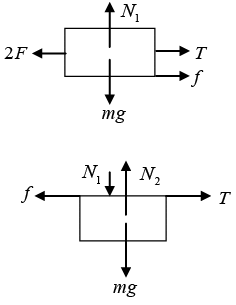
Q.15. The friction coefficient between the two block shown in figure is μ but the floor is smooth.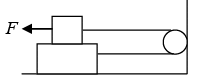 (a) What maximum horizontal force F can be applied without disturbing the equilibrium of the system?
(a) What maximum horizontal force F can be applied without disturbing the equilibrium of the system?
(b) Suppose the horizontal force applied is double that found in part (a). Find the acceleration of the two masses.
F. B. D at Block m
F - T - f = 0
F = T + fT = f For limiting case f = μmg
F = 2f
F = 2 μmg
(b) 2F - f - T = mα
T - f = Mα
T - μmg = MαT = Mα + μmg
2F - μmg - Ma - μmg = mα
Q.16. Consider a particle that feels an angular force only, of the form  Show that
Show that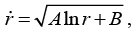 where A and B are constant of integration, determined by the initial condition. (There's nothing all that physical about this force. It simply makes the F = mα equations solvable).
where A and B are constant of integration, determined by the initial condition. (There's nothing all that physical about this force. It simply makes the F = mα equations solvable).
With the given force, equation becomes
The second of these equations gives. Therefore,
where D = eC is a constant of integration, determined by the initial conditions. Substituting this value ofinto the first of equations and then multiplying through by
and integrating, gives
Therefore,
where A ≡ 2D2 and B ≡ 2E.
Q.17. Two blocks A and B of equal mass m are connected through a massless string as shown in figure. Friction is absent everywhere. Now the system is released from the rest,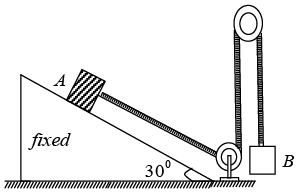 (i) Find the tension in string
(i) Find the tension in string
(ii) Find acceleration of A
T + mg sin θ = ma ; N = mg cos θ; mg - T = ma
3 equations can be solved for T, N and α
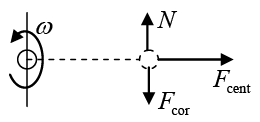
Q.18. A bead slides without friction on a rigid wire rotating at constant angular speed ω. Assume there is not any gravitational field. Find the force exerted by the wire on the bead.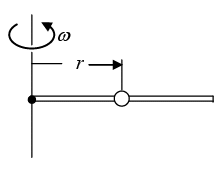
In a coordinate system rotating with the wire the motion is purely radial. The sketch shows the force diagram in the rotating system.
Fcent is the centrifugal force and Fcor is the coriolis force.
Since the wire frictionless, the contact force N is normal to the wire.
(We neglect gravity).
In the rotating system the equations of motion areFcent =
N - Fcor = 0
Using Fcent = mω2r, the first equation gives
which has the solution
r = Aeωt + Be-ωt
where A and B are constants depending on the initial conditions.
The tangential equation of motion, which expresses the fact that there is no tangential acceleration in the rotating system gives
N = Fcor == 2mω2 (Aeωt - Be-ωt
To complete the problem, we must be given the initial conditions which specify A and B.
Q.19. In the figure, the blocks A, B and C have masses of 3 kg and 4 kg and 8 kg respectively. The coefficient of friction between any two surfaces is 0.25. A is at rest by a massless rigid rod fixed to the wall, B and C are connected by a light flexible cord around a fixed frictionless pulley. Find the force necessary to drag C along the horizontal surface to the left at a constant speed. Assume that the arrangement is shown in the figure. i.e., B on C and A on B, is maintained throughout.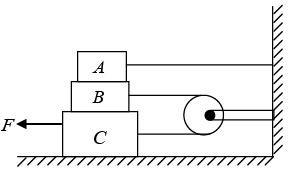
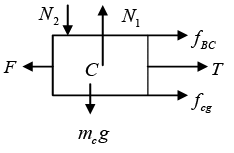
For Block C
N1 Normal force on block C due to ground.
N2 Normal force on block C due to block B.
Fcg is frictional force on block C due to interaction between the ground and block C.
fBC is frictional force on block C due to interaction between surface of block B and C.
N2 + mcg - N1 = 0 (i)
F - fBC - T - fcg = 0 (ii)
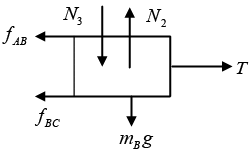
For Block B
fBC is frictional force on Block B due to interaction between the surface of blocks B and C.
fAB is frictional force on Block B due to interaction between surface of Block A and B.
N3 is normal force on Block B due to Block A.
- N3 + N2 - mBg = 0 (iii)
fAB + fBC - T = 0 (iv)
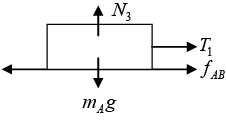
N3 = mAg
f AB = μmAg
N2 = N3 + mBg ⇒ N2 = mAg + mBg from (iii)
fBC = μN2 = μ(mAg + mBg
N1 = N2 + Mcg ⇒ N1 = (mA + mB + mC) g from (i)
fcg = μN1 = μ(mA + mB + mc) g
T = fAB + fBC = μ(2mA + mB)g
F = T + fcg + fBC = μ(2mA + mB) g + μ(mA + mB + mC) g + μ(mA + mB)g
F = μ(4mA + 3mB + 2mC) g = 0.25(4.3 + 3.4 + 2.8) (9.8) = 98 N.
Q.20. A table with smooth horizontal surface is turning at an angular speed ω about its axis. A groove is made on the surface along a radius and a particle is gently placed inside the groove at a distance a from, the centre. Find the speed of the particle with respect to the table as its distance from the centre becomes L.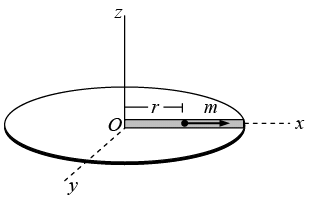
The radial part of acceleration at distance r is given by αr =
Hence there is not any external force in radial direction so
|
61 videos|23 docs|25 tests
|
FAQs on Newton's Laws of Motion: Assignment - Mechanics & General Properties of Matter - Physics
| 1. What are Newton's Laws of Motion? |  |
| 2. What is the significance of Newton's Laws of Motion? |  |
| 3. How can Newton's Laws of Motion be applied in everyday life? |  |
| 4. What are some common misconceptions about Newton's Laws of Motion? |  |
| 5. Can Newton's Laws of Motion be used to explain phenomena beyond classical mechanics? |  |
|
61 videos|23 docs|25 tests
|

|
Explore Courses for Physics exam
|

|

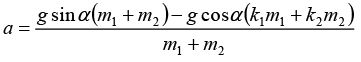 …(i)
…(i)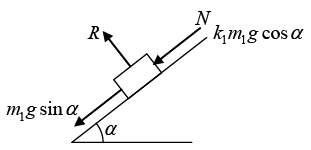
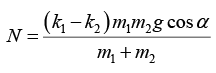
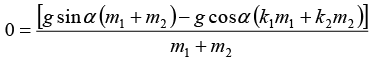 ⇒
⇒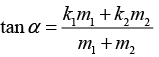
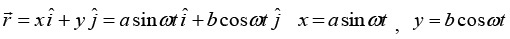
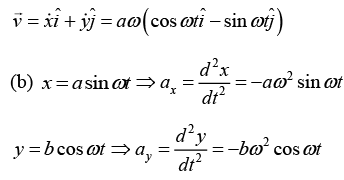

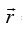 position vector of particle.
position vector of particle.
 F.B.D. of block:
F.B.D. of block:
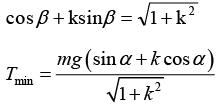
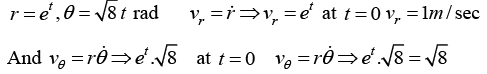
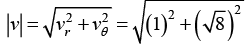 = √9 = 3m/sec
= √9 = 3m/sec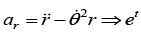 - 8 x et at t = 0, 1 - 8 x 1 = -7m/sec2
- 8 x et at t = 0, 1 - 8 x 1 = -7m/sec2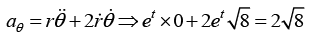
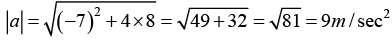
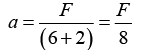
 ∴ F/4 ≤ 0.2 x 2 x 10 ⇒ F/4 ≤ 4 N ⇒ F ≤ 16 N
∴ F/4 ≤ 0.2 x 2 x 10 ⇒ F/4 ≤ 4 N ⇒ F ≤ 16 N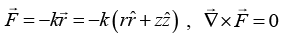
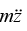 = -kz the motion along z is simple harmonic motion with angular
= -kz the motion along z is simple harmonic motion with angular 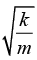
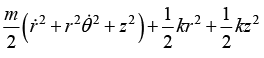
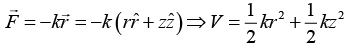
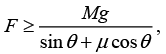
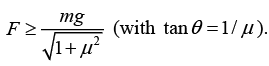
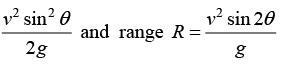 where θ = π/4
where θ = π/4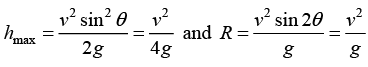
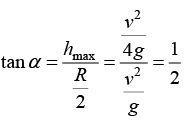
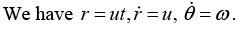
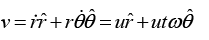
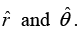 This is obtained from r = (r,θ) = (ut, ωt).
This is obtained from r = (r,θ) = (ut, ωt).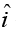 + (u sin ωt - utω cos ωt)
+ (u sin ωt - utω cos ωt)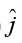
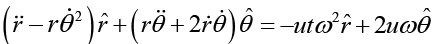
 Let α2 = α then α1 = α/2
Let α2 = α then α1 = α/2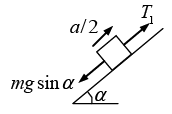 Force on mass 1:
Force on mass 1: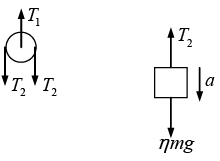
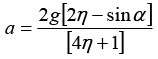
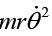 ≡ mrω2 (with r = ℓ sin β), directed radially inward. The forces on the mass are the tension in the string, T , and gravity, mg (see figure). There is no acceleration in the vertical direction, so F = mα in the vertical and radial directions give, respectively,
≡ mrω2 (with r = ℓ sin β), directed radially inward. The forces on the mass are the tension in the string, T , and gravity, mg (see figure). There is no acceleration in the vertical direction, so F = mα in the vertical and radial directions give, respectively,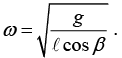
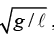 which happens to equal the frequency of a plane pendulum of length ℓ.
which happens to equal the frequency of a plane pendulum of length ℓ.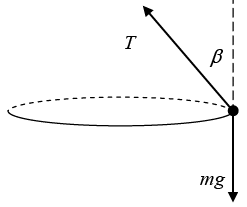
 1g - T = 1α1 ....(i)
1g - T = 1α1 ....(i)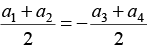
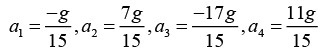
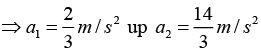 down
down 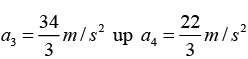 down.
down.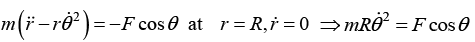
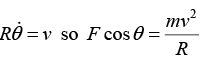
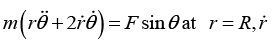
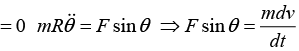
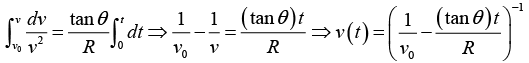
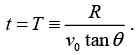

 T = Mα + μmg
T = Mα + μmg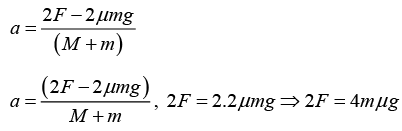
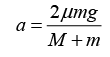
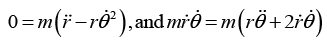
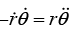 . Therefore,
. Therefore,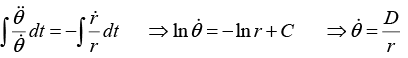
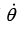 into the first of equations and then multiplying through by
into the first of equations and then multiplying through by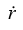 and integrating, gives
and integrating, gives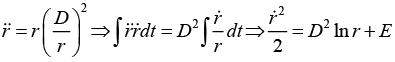
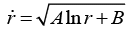
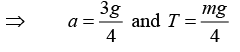
 Fcent =
Fcent =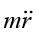
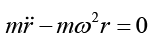
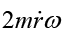 = 2mω2 (Aeωt - Be-ωt
= 2mω2 (Aeωt - Be-ωt