Newton's Universal Law of Gravitation and Gravitational Force | Science Class 9 PDF Download
Introduction
Imagine you have a pen, and when you drop it, it falls to the ground. That pull bringing it down is gravity. It's like a hidden force that makes things fall on Earth. But here's the fun part – gravity isn't just on Earth; it's everywhere, even in space! It's what keeps us on the ground, makes things fall when dropped, and even holds the Moon in the sky. Gravity is like a magical connection that pulls everything together.
Gravitation
- The paths followed by the planets around the sun and by the satellites around the planets are known as orbits.
- According to Newton's first law of motion, these planets and satellites can move in circular orbits only if some force is acting on them. The mystery of the motion of all these heavenly bodies (i.e. planets and satellites) in nearly circular orbits was solved by Isaac Newton when he observed an apple fall from a tree towards the earth.
 Issac Newton sitting under the Apple tree
Issac Newton sitting under the Apple tree - Therefore, he proposed that all particles or objects in the universe attract each other in the same manner as the earth attracted the apple.
"The force of attraction between any two particles in the universe is called gravitation or gravitation force".

Universal Law of Gravitation
Newton's universal law of gravitation states that "Every particle in the universe attracts every other particle with of force which is directly proportional to the product of two masses and inversely proportional to the square of the distance between them ".
- The direction of the force is along the line joining the two masses.
- If m1 and m2 are the masses of two bodies separated by a distance d and F is the force of attraction between them, then we get:
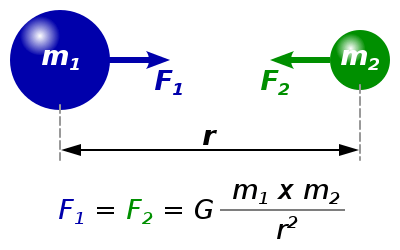
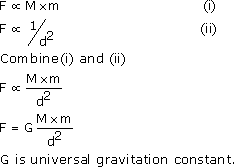
- F =
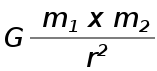 where G is a constant of proportionality known as the constant of universal gravitation and is equal to:
where G is a constant of proportionality known as the constant of universal gravitation and is equal to:
Fd2 = Gm1m2
G = Fd2 / m1m2 - If m1 = m2 = 1kg and d = 1m, then
- The universal gravitational constant is the force of attraction (in Newton) between two bodies of mass 1 kg each lying 1-metre distance apart.
- Unit of gravitational constant:
G = Fd2 / m1m2
In SI unit, G = Nm2 / (kg x kg) = Nm2 kg-2
In the CGS unit, G = dyn cm2 g-2. - The value of G = 6.7 ✖ 10 -11Nm2kg-2
Characteristics of Gravitational Force
- The gravitational force between two bodies or objects does not need any contact between them. It means the gravitational force is action at a distance.
- The gravitational force between two bodies varies inversely proportional to the square of the distance between them. Hence, gravitational force is an inverse square force.
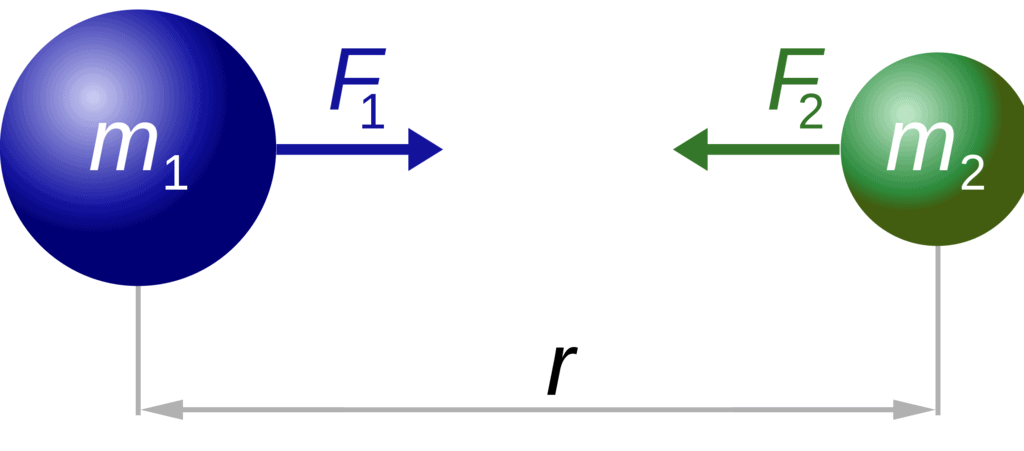
- The gravitational forces between two bodies or objects form an action-reaction pair. If object A attracts object B with a force F1 and object B attracts object A with a force F2, then F1 = F2.
Do You Know?
- The value of G = 6.67 × 10-11 N m2 kg-2 or 6.67 × 10-8 dyn cm2 g-2.
- The value of G is same throughout the universe and hence G is known as universal gravitational constant.
- Value of G was determined in laboratory by Sir Henry Cavendish.
- Since the value of G is very small, so the gravitational force is a very weak force.
- The gravitational force between a body on the earth is called gravity.
Importance of the Universal Law of Gravitation
The Universal law of gravitation given by Newton has explained successfully several phenomena such as:
- The gravitational force of attraction of the Earth is responsible for binding all terrestrial objects on the Earth.
- The gravitational force of the Earth is responsible for holding the atmosphere around the Earth.
- The gravitational force of the Earth is also responsible for the rainfall and snowfall on the Earth.
- The flow of water in rivers is also due to gravitational force of the Earth on water.
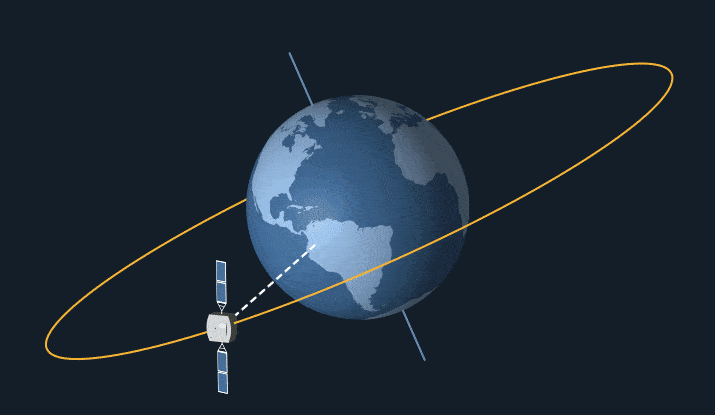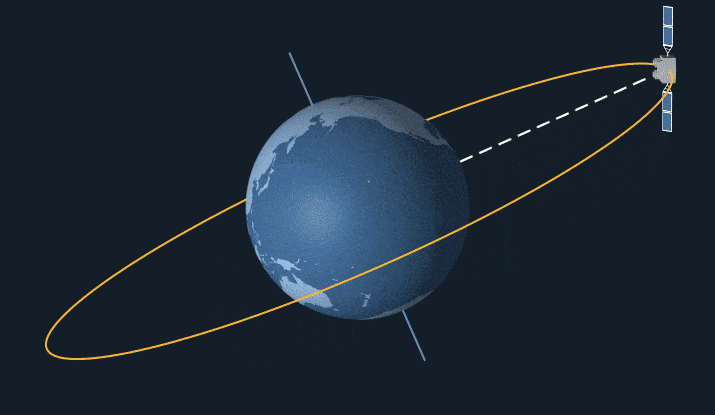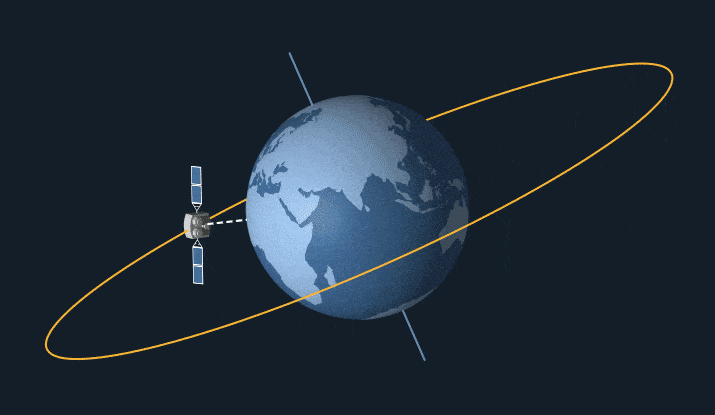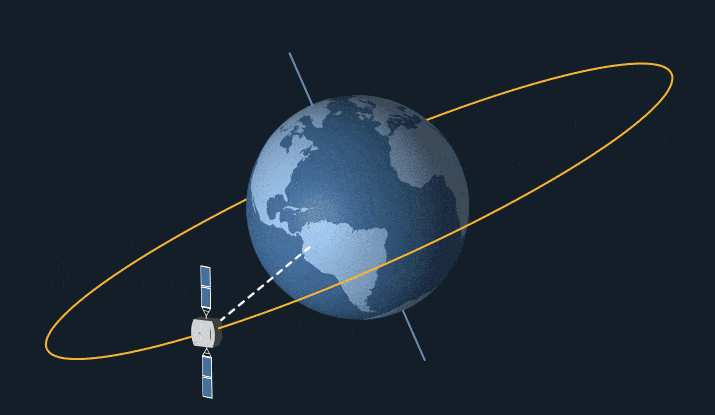 A Satellite Revolving Around the Earth
A Satellite Revolving Around the Earth - The moon revolves around the Earth on account of the gravitational pull of the Earth on the Moon. Even all artificial satellites revolve around the Earth on account of the gravitational pull of the Earth on the satellites.
- The predictions about solar and lunar eclipses made on the basis of this law always come out to be true. The gravitational force plays an important role in nature.
- All the planets revolve around the sun due to the gravitational force between the sun and the planets. The force required by a planet to move around the sun in a circular path (known as centripetal force) is provided by the gravitational force of attraction between the planet and the sun. Thus, gravitational force is responsible for the existence of the solar system.
- Tides in oceans are formed due to the gravitational force between the moon and the water in oceans.
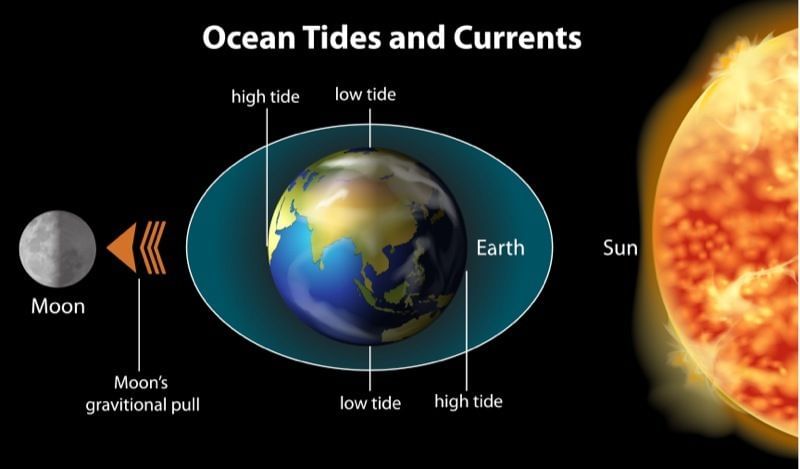 Tides in the Ocean are formed due to Gravitational Force
Tides in the Ocean are formed due to Gravitational Force - The gravitational force between a planet and its satellite (i.e., moon) decides whether a planet has a moon or not.
Interesting Fact:
Since the gravitational force of the planets like Mercury and Venus is very small, therefore, these planets do not have any satellite or moon.
Now you must be thinking that Pluto also has small mass then why it has Moons?
This is because Mercury and Venus are closer to the Sun, which has a stronger gravitational pull that has likely engulfed any potential moons for Mercury and Venus.
- We stay on the earth due to the gravitational force between the earth and us.
Gravitational Force Between Light Objects and Heavy Objects
The formula applied for calculating gravitational force between light objects and heavy objects is the same, i.e.,  The formula for the force between Objects
The formula for the force between Objects
Let us take three cases:
(i) When two bodies of mass 1 kg each are 1 meter apart.
Sol.
m1= m2 = 1 kg, r = 1 m
Taking G = 6·67 × 10-11 Nm2/kg2, we obtain the gravitational force of attraction,
which is extremely small. Hence, we conclude that though every pair of two objects exert gravitational pull on each other, yet they cannot move towards each other because this gravitational pull is too weak.
(ii) When a body of mass 1 kg is held on the surface of Earth.
Sol.
Here, m1 = 1 kg
m2 = mass of Earth = 6 × 1024 kg
r = distance of body from centre of Earth = radius of Earth = 6400 km = 6.4 × 103km = 6·4 × 106 m
The gravitational force of attraction between the body and Earth,
It means that the Earth exerts a gravitational force of 9·8 N on a body of mass one kg. This force is much larger compared to the force when both bodies are lighter. That is why when a body is dropped from a height, it falls to the Earth.
(iii) When both bodies are heavy.
Sol.
Let us calculate the gravitational force of attraction between Earth and the Moon.
Mass of Earth, m1 = 6 × 1024 kg
Mass of Moon, m2 = 7.4 × 1022 kg
Distance between Earth and Moon, r = 3.84 × 105 km = 3.84 × 108 m
Gravitational constant, G = 6·67 × 10-11 Nm2/kg2
The gravitational force between Earth and the Moon,
which is really large. It is this large gravitational force exerted by the Earth on the Moon, that makes the Moon revolve around the Earth.
Solved Examples
Q. Find the gravitational force of attraction between two spheres each of mass 1000 kg. The distance between the centers of the spheres is 0.5 m.
Solution: Mass = m1 = m2 = 1000 kg
Distance between the centers = d = 0.5 m
Gravitational constant = G = 6.673 × 10-11 Nm2kg-2
Gravitational force = F = ?
F = Gm1m2/d2
F = 6.673 × (10)-11 × 1000 × 1000/(0.5)2
= 6.673 * (10)-11 * (10)6 /0.25
= 6.673 * (10)-5 /0.25
= 26.692 * (10)-5
= 2.67 × 10-4 N
Q. The gravitational force between two identical lead spheres kept at 1 m apart is 0.006673 N. Find their masses.
Solution: Gravitational force = F = 0.006673 N
Gravitational constant = G = 6.673 × 10-11 Nm2kg-2
Distance between the masses = d = 1m
Mass = m1 = m2 =?
F = Gm1m2/d2
F = m2/d2 (Let m1 = m2 = m)
m2 = F*d2/G
m2 = 0.006673 * (1)-3 / 6.673*(10)-11
Taking square root on both side
m = 104 = 10000 kg each
Therefore, mass of each lead sphere is 10000 kg.
|
84 videos|478 docs|60 tests
|
FAQs on Newton's Universal Law of Gravitation and Gravitational Force - Science Class 9
| 1. What is centripetal force? |  |
| 2. What is the Universal Law of Gravitation? |  |
| 3. What are the characteristics of gravitational force? |  |
| 4. Why is the Universal Law of Gravitation important? |  |
| 5. How does Newton's Universal Law of Gravitation explain the gravitational force between light objects and heavy objects? |  |

















