Notes: Arithmetic Sequence | Mathematics for Grade 10 PDF Download
Introduction
The arithmetic sequence is the sequence where the common difference remains constant between any two successive terms. Let us recall what is a sequence. A sequence is a collection of numbers that follow a pattern. For example, the sequence 1, 6, 11, 16, … is an arithmetic sequence because there is a pattern where each number is obtained by adding 5 to its previous term. We have two arithmetic sequence formulas.
- The formula for finding nth term of an arithmetic sequence
- The formula to find the sum of first n terms of an arithmetic sequence
If we want to find any term in the arithmetic sequence then we can use the arithmetic sequence formula. Let us learn the definition of an arithmetic sequence and arithmetic sequence formulas along with derivations and a lot more examples for a better understanding.
What is an Arithmetic Sequence?
An arithmetic sequence is defined in two ways. It is a "sequence where the differences between every two successive terms are the same" (or) In an arithmetic sequence, "every term is obtained by adding a fixed number (positive or negative or zero) to its previous term". The following is an arithmetic sequence as every term is obtained by adding a fixed number 4 to its previous term.
Arithmetic Sequence Definition & Example
In arithmetic sequence, every term is obtained by adding a fixed number to its previous term.
Example: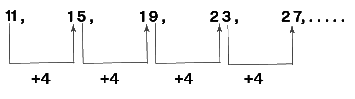 Arithmetic Sequence Example
Arithmetic Sequence Example
Consider the sequence 3, 6, 9, 12, 15, .... is an arithmetic sequence because every term is obtained by adding a constant number (3) to its previous term.
Here,
- The first term, a = 3
- The common difference, d = 6 - 3 = 9 - 6 = 12 - 9 = 15 - 12 = ... = 3
Thus, an arithmetic sequence can be written as a, a + d, a + 2d, a + 3d, .... Let us verify this pattern for the above example.
a, a + d, a + 2d, a + 3d, a + 4d, ... = 3, 3 + 3, 3 + 2(3), 3 + 3(3), 3 + 4(3),... = 3, 6, 9, 12,15,....
A few more examples of an arithmetic sequence are:
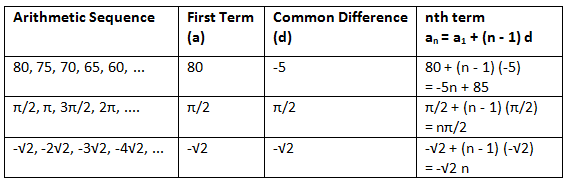
- 5, 8, 11, 14, ...
- 80, 75, 70, 65, 60, ...
- π/2, π, 3π/2, 2π, ....
- -√2, -2√2, -3√2, -4√2, ...
Arithmetic Sequence Formula
The first term of an arithmetic sequence is a, its common difference is d, n is the number of terms. The general form of the AP is a, a+d, a+2d, a+3d,......up to n terms. We have different formulas associated with an arithmetic sequence used to calculate the nth term, the sum of n terms of an AP, or the common difference of a given arithmetic sequence.
Arithmetic Sequence Formulas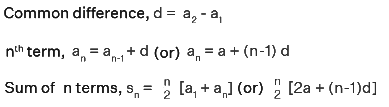
The arithmetic sequence formula is given as,
- Nth Term: an = a + (n-1)d
- Sn = (n/2) [2a + (n - 1)d]
- d = an - an-1
Nth Term of Arithmetic Sequence
The nth term of an arithmetic sequence a1, a2, a3, ... is given by an = a1 + (n - 1) d. This is also known as the general term of the arithmetic sequence. This directly follows from the understanding that the arithmetic sequence a1, a2, a3, ... = a1, a1 + d, a1 + 2d, a1 + 3d,... The following table shows some arithmetic sequences along with the first term, the common difference, and the nth term.
Arithmetic Sequence Recursive Formula
The above formula for finding the nth term of an arithmetic sequence is used to find any term of the sequence when the values of 'a1' and 'd' are known. There is another formula to find the nth term which is called the "recursive formula of an arithmetic sequence" and is used to find a term (an) of the sequence when its previous term (an-1) and 'd' are known. It says
an = an-1 + d
This formula just follows the definition of the arithmetic sequence.
Example: Find a21 of an arithmetic sequence if a19 = -72 and d = 7.
By using the recursive formula,
a20 = a19 + d = -72 + 7 = -65
a21 = a20 + d = -65 + 7 = -58
Therefore, a21 = -58.
Arithmetic Series
The sum of the arithmetic sequence formula is used to find the sum of its first n terms. Note that the sum of terms of an arithmetic sequence is known as arithmetic series. Consider an arithmetic series in which the first term is a1 (or 'a') and the common difference is d. The sum of its first n terms is denoted by Sn. Then
- When the nth term is NOT known: Sn = n/2 [2a1 + (n-1) d]
- When the nth term is known: Sn = n/2 [a1 + an]
Example: Ms. Natalie earns $200,000 per annum and her salary increases by $25,000 per annum. Then how much does she earn at the end of the first 5 years?
The amount earned by Ms. Natalie for the first year is, a = 2,00,000. The increment per annum is, d = 25,000. We have to calculate her earnings in the first 5 years. Hence n = 5. Substituting these values in the sum sum of arithmetic sequence formula,
Sn = n/2 [2a1 + (n-1) d]
⇒ Sn = 5/2(2(200000) + (5 - 1)(25000))
= 5/2 (400000 +100000)
= 5/2 (500000)
= 1250000
She earns $1,250,000 in 5 years. We can use this formula to be more helpful for larger values of 'n'.
Sum of Arithmetic Sequence
Let us take an arithmetic sequence that has its first term to be a1 and the common difference to be d.
Then the sum of the first 'n' terms of the sequence is given by
Sn = a1 + (a1 + d) + (a1 + 2d) + … + an ... (1)
Let us write the same sum from right to left (i.e., from the nth term to the first term).
Sn = an + (an – d) + (an – 2d) + … + a1 ... (2)
Adding (1) and (2), all terms with 'd' get canceled.
2Sn = (a1 + an) + (a1 + an) + (a1 + an) + … + (a1 + an)
2Sn = n (a1 + an)
Sn = [n(a1 + an)]/2
By substituting an = a1 + (n – 1)d into the last formula, we have
Sn = n/2 [a1 + a1 + (n – 1)d] (or)
Sn = n/2 [2a1 + (n – 1)d]
Thus, we have derived both formulas for the sum of the arithmetic sequence.
Difference Between Arithmetic Sequence and Geometric Sequence
Here are the differences between arithmetic and geometric sequence: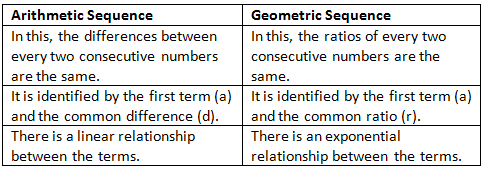
Important Notes on Arithmetic Sequence:
- In arithmetic sequences, the difference between every two successive numbers is the same.
- The common difference of an arithmetic sequence a1, a2, a3, ... is, d = a2 - a1 = a3 - a2 = ...
- The nth term of an arithmetic sequence is an = a1 + (n−1)d.
- The sum of the first n terms of an arithmetic sequence is Sn = n/2[2a1 + (n − 1)d].
- The common difference between arithmetic sequences can be either positive or negative or zero.
|
137 videos|84 docs|44 tests
|




















