Notes: Enlargement | Graphs for MAT PDF Download
| Table of contents |

|
| Introduction |

|
| Fractional Enlargements and Finding the Centre of Enlargement |

|
| Negative Enlargements - Higher |

|
| Combining Transformations - Higher |

|
Introduction
- Enlarging a shape changes its size.

- All the lengths of the sides of the triangle X'Y'Z' are twice the lengths of the sides of the original triangle XYZ. The triangle XYZ has been enlarged by a scale factor of 2.
- Enlargement is an example of a transformation. A transformation is a way of changing the size or position of a shape.
- To enlarge a shape, a centre of enlargement is required. When a shape is enlarged from a centre of enlargement, the distances from the centre to each point are multiplied by the scale factor.
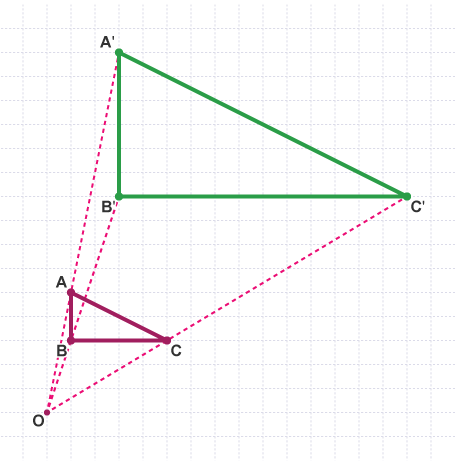
- The lengths in triangle A'B'C' are three times as long as the lengths of the side of triangle ABC. The distance from O to triangle A'B'C' is three times the distance from O to ABC.

- The triangle ABC has been enlarged by a scale factor of 3 about the centre of enlargement O.
Two pieces of information are needed to enlarge a shape:
- the scale factor
- the centre of enlargement
Scale factors
Scale factors can increase or decrease the size of a shape.
Example:
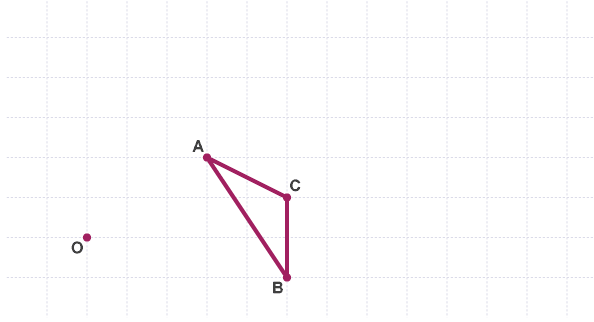
Enlarge the triangle ABC by a scale factor of 2 about the centre of enlargement O
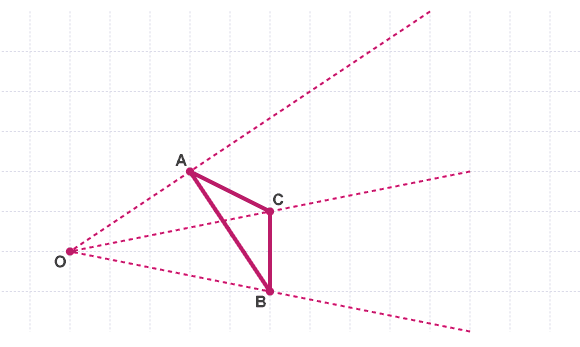
First, draw ray lines from O to each corner of the triangle and extend them
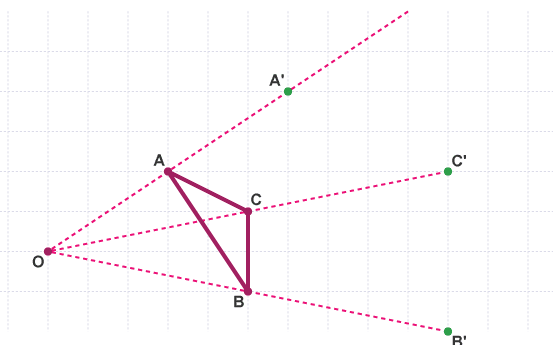
Next, measure the distance from O to each corner of ABC. Multiply this distance by two and plot the points A', B', and C'
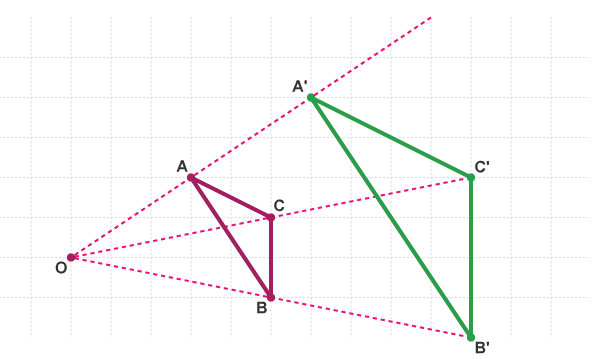
Finally, join up the points A' B' C'
Alternatively, the distances OA, OB and OC can be shown as vectors. OA = 
so under a scale factor of 2 OA' = 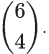
The centre of enlargement may be outside a shape or it may be inside a shape, on an edge or at a vertex.
The image may overlap the shape or one may be inside the other.
Solved Example
Example 1: Enlarge the triangle PQR by a scale factor of 3 about the centre of enlargement O.

First draw ray lines from O to each vertex of the triangle and extend them.
Next measure the distance from O to each vertex of PQR. Multiply this distance by 3 and plot the points P' Q' and R'.
Finally join up the points P' Q' R'.
Example 2: What scale factor has been used to enlarge the shape OXYZ to OX'Y'Z'?
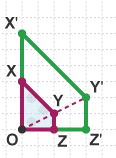
Each side in the shape OX'Y'Z' is twice as long as the side in the shape OXYZ.
OXYZ has been enlarged by a scale factor of 2 about the centre of enlargement O.
Fractional Enlargements and Finding the Centre of Enlargement
Fractional enlargements
When a shape is enlarged by a scale factor between 0 and 1, the image is smaller than the original shape. The triangle ABC is enlarged by a scale factor of 1/3. All the sides of triangle A'B'C' are one third as long as the sides of the original triangle ABC.
The triangle ABC is enlarged by a scale factor of 1/3. All the sides of triangle A'B'C' are one third as long as the sides of the original triangle ABC.
Example:
Enlarge the triangle ABC by a scale factor of 1/2 about the centre of enlargement O.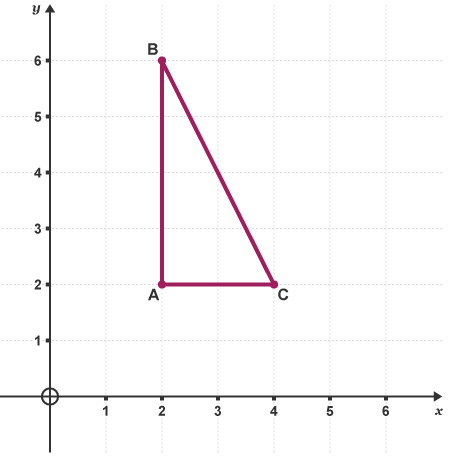 First, draw ray lines from O to each corner of the triangle.
First, draw ray lines from O to each corner of the triangle.
Next, measure the distance from O to each corner of ABC. Divide the distance by two and plot the points A' B' and C'. Alternatively these distances can be shown as vectors. OA = 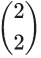
so under a scale factor of 1/2 , OA' = 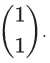
Finally, join up the points A' B' C'.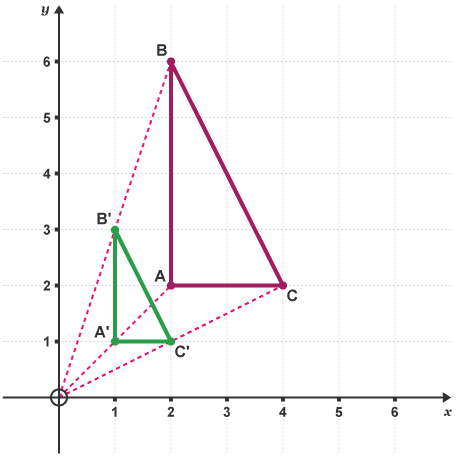
Finding the centre of enlargement
To find the centre of enlargement, draw ray lines from the corners of the image through the corners of the original shape.
Example:
Describe the transformation of the triangle RST.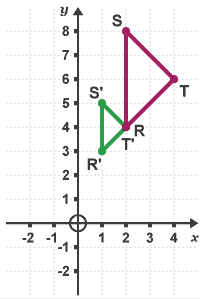
Draw ray lines from the corners of triangle RST through the corners of R'S'T' until they cross. This is the centre of enlargement
Negative Enlargements - Higher
An enlargement with a negative scale factor produces an image on the other side of the centre of enlargement. The image appears upside down.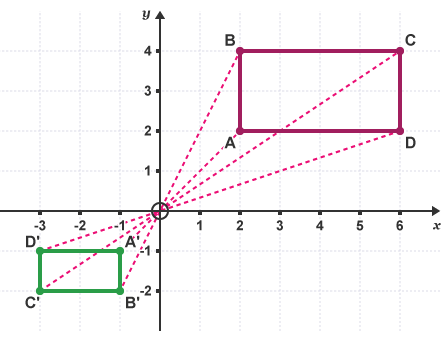
The rectangle ABCD has been enlarged by a scale factor of 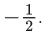
The lengths in rectangle A'B'C'D' are 1/2 times as long as rectangle ABCD. The distance from O to A'B'C'D' is half the distance from O to ABCD.
Example: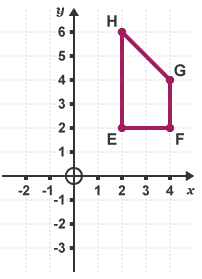
Enlarge the quadrilateral EFGH by a scale factor of -½ about the centre of enlargement O
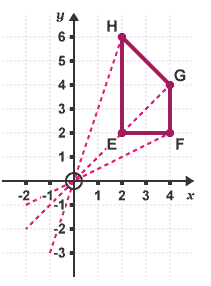
First, draw ray lines from each corner of the quadrilateral to O and extend them
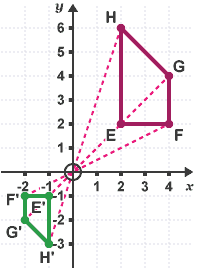
Next, measure the distance from O to each corner of EFGH. Divide the distance by two and plot the points E' F' G' and H' on the other side of the centre of enlargement. Finally, join up the points E' F' G' and H'
Note: An enlargement by a scale factor of -1 is the same as a rotation of 180°.
Combining Transformations - Higher
Sometimes a shape is transformed using more than one step, for example a reflection followed by a rotation.
The combination of transformations can usually be described as a single transformation.
Example: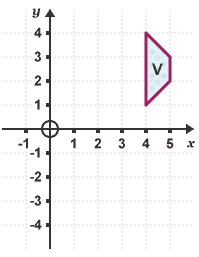
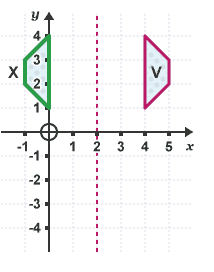
Draw the mirror line x = 2. Reflect the shape V in this line and label it X
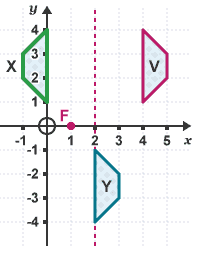
Rotate the shape X 180° about the point (1,0). Label this image Y
To describe the transformation from V to Y as a single transformation, it is a translation by the vectors 
Solved Example
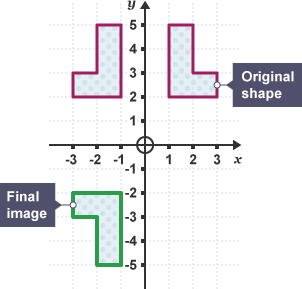
Example: Describe a single transformation that is equivalent to a reflection in the y-axis followed by a reflection in the x-axis.
Drawing a diagram will help.
The single transformation is a rotation 180° about the origin.
|
4 videos|5 docs
|

|
Explore Courses for MAT exam
|

|
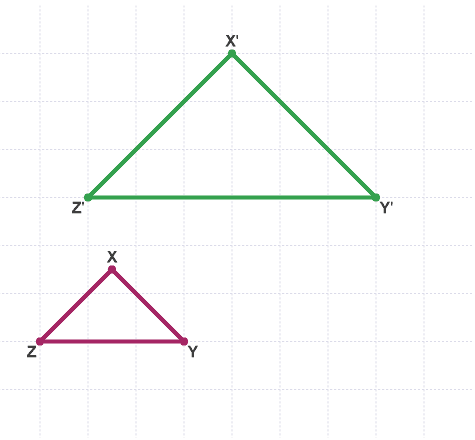

 The single transformation is a rotation 180° about the origin.
The single transformation is a rotation 180° about the origin.















