Notes: Geometric Sequence | Mathematics for Grade 10 PDF Download
Introduction
A geometric sequence is a special type of sequence. It is a sequence in which every term (except the first term) is multiplied by a constant number to get its next term. i.e., To get the next term in the geometric sequence, we have to multiply with a fixed term (known as the common ratio), and to find the preceding term in the sequence, we just have to divide the term by the same common ratio. Here is an example of a geometric sequence is 3, 6, 12, 24, 48, ...... with a common ratio of 2. The common ratio of a geometric sequence can be either negative or positive but it cannot be 0. Here, we learn the following geometric sequence formulas:
- The nth term of a geometric sequence
- The recursive formula of a geometric sequence
- The sum of a finite geometric sequence
- The sum of an infinite geometric sequence
The geometric sequences can be finite or infinite. Here we shall learn more about each of the above-mentioned geometric sequence formulas along with their proofs and examples.
What is a Geometric Sequence?
A geometric sequence is a special type of sequence where the ratio of every two successive terms is a constant. This ratio is known as a common ratio of the geometric sequence. In other words, in a geometric sequence, every term is multiplied by a constant which results in its next term. So a geometric sequence is in form a, ar, ar2... where 'a' is the first term and 'r' is the common ratio of the sequence. The common ratio can be either a positive or a negative number.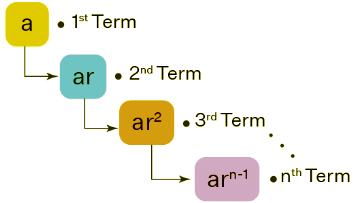
Geometric Sequence Examples
- 1/4, 1/8, .... is a geometric sequence where a = 1/4 and r = 1/2
- -4, 2, -1, 1/2, -1/4, ... is a geometric sequence where a = -4 and r = -1/2
- π, 2π, 4π, 8π,.... is a geometric sequence where a = π and r = 2
- √2, -√2, √2, -√2, ... is a geometric sequence where a = √2 and r = -1
There are two types of geometric sequences based on the number of terms in them. They are
- Finite geometric sequences
- Infinite geometric sequences
Finite geometric sequence
A finite geometric sequence is a geometric sequence that contains a finite number of terms. i.e., its last term is defined. For example 2, 6, 18, 54, ....13122 is a finite geometric sequence where the last term is 13122.
Infinite geometric sequence
An infinite geometric sequence is a geometric sequence that contains an infinite number of terms. i.e., its last term is not defined. For example, 2, −4, 8, −16, ... is an infinite sequence where the last term is not defined.
Geometric Sequence Formulas
Here is the list of all geometric sequence formulas. For any geometric sequence a, ar, ar2, ar3, ...
- nth term, an = arn - 1 (or) an = r an - 1
- Sum of the first n terms, Sn = a(rn - 1) / (r - 1) when r ≠ 1 and Sn = na when r = 1.
- Sum of infinite terms, S∞ = a / (1 - r) when |r| < 1 and S∞ diverges when |r| ≥ 1.
For a geometric sequence a, ar, ar2 , .....
- nth term,
an = arn-1 - Sum of n terms,
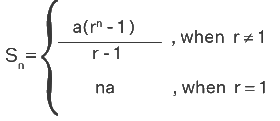
- Sum of infinite terms,
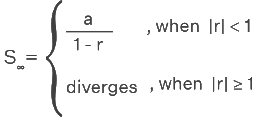
Let us study each and every formula one by one here.
nth Term of Geometric Sequence Formula
We have already seen that a geometric sequence is of the form a, ar, ar2, ar3, ...., where 'a' is the first term and 'r' is the common ratio. Here,
- The 1st term, a1 = a = a r1-1
- The 2nd term, a2 = a r = a r2-1
- The 3rd term, a3 = a r2 = a r3-1
So in general, the nth term of a geometric sequence is,
- an = arn-1
Here,
- a = first term of the geometric sequence
- r = common ratio of the geometric sequence
- an = nth term
There is another formula used to find the nth term of a geometric sequence given its previous term and the common ratio which is called the recursive formula of the geometric sequence.
Recursive Formula of Geometric Sequence
We know that in a geometric sequence, a term (an) is obtained by multiplying its previous term (an - 1) by the common ratio (r). So by the recursive formula of a geometric sequence, the nth term of a geometric sequence is,
- an = r an - 1
Here,
- an = nth term
- an - 1 = (n - 1)th term
- r = common ratio
Example: Find a15 of a geometric sequence if a13 = -8 and r = 1/3.
By the recursive formula of geometric sequence,
a14 = r a13 = (1/3) (-8) = -8/3
Applying the same formula again,
a15 = r a14 = (1/3) (-8/3) = -8/9.
Therefore, a15 = -8/9.
Sum of Finite Geometric Sequence Formula
The sum of a finite geometric sequence formula is used to find the sum of the first n terms of a geometric sequence. Consider a geometric sequence with n terms whose first term is 'a' and common ratio is 'r'. i.e., a, ar, ar2, ar3, ... , arn-1. Then its sum is denoted by Sn and is given by the formula:
- Sn = a(rn - 1) / (r - 1) when r ≠ 1 and Sn = na when r = 1.
Let us derive the formula now.
Sum of Finite Geometric Sequence Proof
We have Sn = a + ar + ar2 + ar3 + ... + arn-1... (1)
Multiply both sides by r,
rSn = ar + ar2 + ar3 + ... + arn... (2)
Subtracting (1) from (2),
rSn - Sn = arn - a
Sn (r - 1) = a (rn - 1)
Sn = a(rn - 1) / (r - 1)
Since (r - 1) is in its denominator, it is defined only when r ≠ 1. If r = 1, the sequence looks like a, a, a, ... and the sum of the first n terms, in this case, = a + a + a + ... (n times) = na.
Thus, we have derived the formula of the sum of a finite geometric sequence.
Sum of Infinite Geometric Sequence Formula
The sum of an infinite geometric sequence formula gives the sum of all its terms and this formula is applicable only when the absolute value of the common ratio of the geometric sequence is less than 1 (because if the common ratio is greater than or equal to 1, the sum diverges to infinity).
i.e., An infinite geometric sequence- converges (to finite sum) only when |r| < 1
- diverges (to infinity) when |r| ≥ 1
Consider an infinite geometric sequence a, ar, ar2, ar3, ... The sum of its infinite terms is denoted by S∞. Then
- S∞ = a / (1 - r), when |r| < 1 and S∞ diverges when |r| ≥ 1.
Let us derive the formula now.
Sum of Infinite Geometric Sequence Proof
We have S∞ = a + ar + ar2 + ar3+ ... ...(1)
Multiplying both sides by r,
rS∞ = ar + ar2 + ar3+ ... ... (2)
Subtracting (2) from (1),
S∞ - rS∞ = a
S∞ (1 - r) = a
S∞ = a / (1 - r)
Hence we have derived the formula of the sum of an infinite geometric sequence.
Geometric Sequence vs Arithmetic Sequence
Here are a few differences between geometric sequence and arithmetic sequence shown in the table below: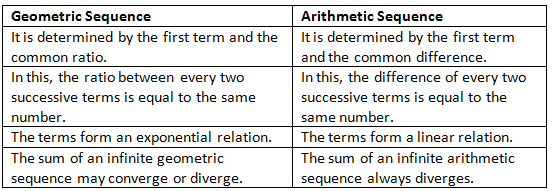
Important Notes on Geometric Sequence:
- In a geometric sequence, every term is obtained by multiplying its previous term by a constant (r, which is called the common ratio).
- If r > 1, then the terms are in ascending order.
- When r = 1, and the first term of a geometric sequence is 'a' then its sum is a · n.
- When r ≥ 1, the infinite geometric sequence diverges.
|
137 videos|83 docs|44 tests
|















