Notes: Knowing our numbers | Mathematics & Pedagogy Paper 2 for CTET & TET Exams - CTET & State TET PDF Download
| Table of contents |

|
| The Place Value |

|
| Large Numbers |

|
| Ascending Order and Descending Order |

|
| Estimation |

|
| ROMAN NUMERALS |

|
| Rules of the Roman Numeral System |

|
| Solved Examples |

|
| BODMAS Rule |

|
Numbers are a fundamental part of mathematics and our everyday lives. They help us count, measure, and understand quantities. You'll explore different types of numbers and learn how to work with them in various mathematical operations.
 Example of Place Value
Example of Place Value
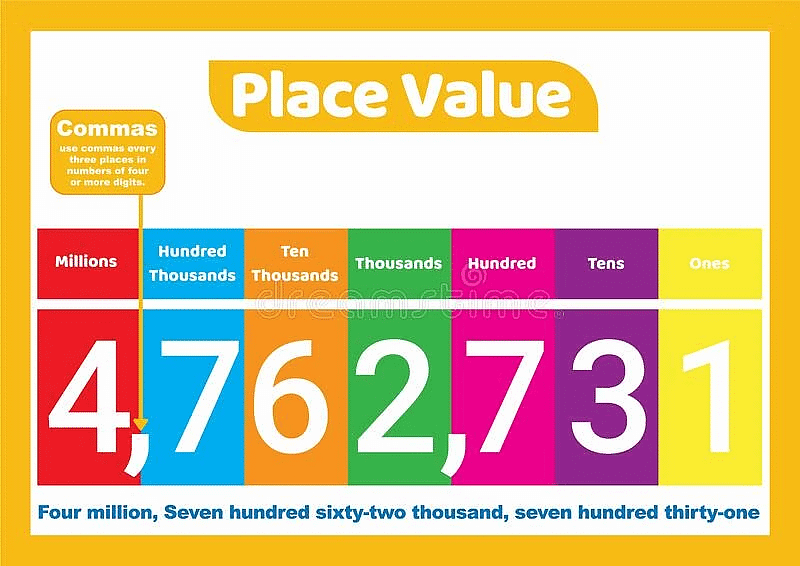
The Place Value
We have done the concept of place value in earlier classes and might remember the expansion of a two-digit number. Let us hit the refresh button and revisit the general forms of numbers.
Example: Two-digit number 67.
Now when we start from the right i.e from 7 to 6, the place of seven is known as Ones and that for 6 is known as Tens.
Hence if it’s a three-digit number, the places will be ones, tens and hundreds from right to left. Similarly, for a 4 digit number, it’ll be ones, tens, hundreds and thousands. For a five-digit number, the leftmost place will be called ten thousand. Let’s understand this concept.
Suppose we have a 3 digit number: 345. We can label the places as follows.
Place | Hundreds | Tens | Ones |
Digit | 3 | 4 | 5 |
The value of hundreds place is 100. Similarly, for tens and ones, it is 10 and 1 respectively. As you might remember,
| Place value = Place × Digit |
Using the above knowledge, the number 345 can be expanded as:
=3×100 + 4×10 + 5×1 = 345.
Similarly, a 5 digit number 54672 is expanded as
= 5×10000 + 4×1000 + 6×100 + 7×10 + 2×1
Large Numbers
Till now we have been studying numbers up to 5 digits. Let us expand our scope to large numbers, starting off with the following knowledge:
1. The Indian System of Numeration: (i.e. General Form of Numbers)
Places (left to right in order): Ten crores – Crore – Ten lakhs – Lakhs – Ten thousands – Thousands – Hundreds – Tens – Ones
2. The International System of Numeration:
Places (left to right in order): Hundred million – Ten million – Million – Hundred thousand – Ten thousand – Thousand – Hundred – Tens – Ones
Thus we can expand our understanding of the general form of numbers with 9 digits and more.
Example: The expansion of 265478100 is given as.
265478100 = 2×100000000 + 6×10000000 + 5×1000000 + 4×100000 + 7×10000 + 8×1000 + 1×100 + 0×10 + 0×1.
Further, its number name is given as:
- Twenty-six crore fifty-four lakh seventy-eight thousand one hundred (Indian System)
- Two hundred sixty-five million four hundred seventy-eight thousand one hundred (International system)
Using Commas
Commas are generally used to ease the process of reading and writing large numbers. For the Indian system of numeration, commas are used to mark thousands, lakhs and crores. On the contrary, for the International system of numeration, commas are used to mark thousands and millions.
Example: 72705062 can be written as 7,27,05,062 in the Indian system whereas it is written as 72,705,062 in the international system.
Comparing Numbers
With all the information about the general form of numbers, we can easily compare them. When we compare two numbers we start comparing the digits of each number from left. The two scenarios that arise are- they can have an unequal or equal number of digits.
In the first case i.e. for comparing numbers with an unequal number of digits, obviously, the number with more digits is greater.
Example: Among 12, 123, 1234 and 12345 the greatest number is 12345 since it is a 5 digit number.
For comparison of two numbers having an equal number of digits, we compare the digits at the places starting from left.
Example: If we need to compare 4567 and 4578, we start by looking at the digits of both numbers at the leftmost place(here thousand).
As both are the same, we move on to the hundred places. Here also the digit 5 is the same in both. Further, we move on to the tens place. Here we can see that the digit(6) at tens place of 4567 is less than the digit(7) at tens place of 4578. Hence, we conclude that 4578 is greater than 4567.
Ascending Order and Descending Order
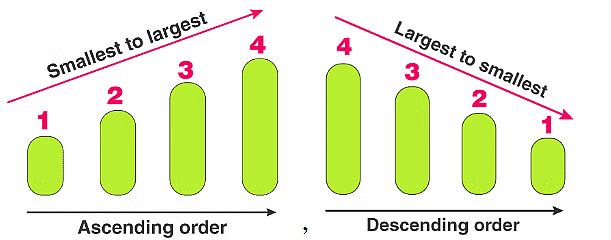
As now know how to compare numbers, we can easily arrange a given set of numbers. We can either arrange the numbers in increasing order (known as Ascending order) or in decreasing order (known as Descending order).
Example: 12, 18, 45, 39, 20, 1, 5
(i) Ascending order: 1, 5, 12, 18, 20, 39, 45
(ii) Descending order: 45, 39, 20, 18, 12, 5, 1
Note: Observe that ascending and descending orders are reverse of each other.
Solved Example
Ques: Arrange the following in ascending order:
847, 9754, 8320, 571
Ans: The numbers in ascending order are as follows:
571, 847, 8320, 9754
Estimation
Often in real-life situations, knowing the exact number of things is not as important. An estimate is far more practical and easier to calculate. For example, the Prime Minister of India does not need to know the exact number of students pursuing higher education in India. He only requires an estimate so he can form policies accordingly.
To find an estimate is easier, cheaper and less time-consuming than an actual count in many cases. If the situation does not warrant an exact count, estimation is a way to go. Let us learn a few methods related to estimation.
1. Rounding off to nearest Tens
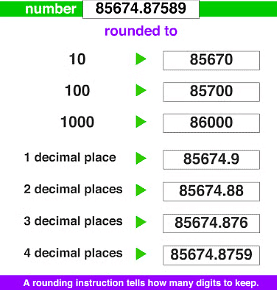
Let us take an example of three numbers 14, 15 and 16. We are to round off these numbers to the nearest tens place. Now imagine these numbers on a number scale. Is 14 closer to 10 or to 20. It is closer to 10, so we can round off 14 as 10. Similarly, 16 is closer to 20, and hence we can round off 16 as 20. 15 is equidistant from both 10 and 20. It is the general practice to round up, which means 15 will be rounded off to 20 as well.
In conclusion, the numbers ending in 1, 2, 3, and 4 are rounded down, while those ending in 5, 6, 7, 8 and 9 are rounded up to the nearest tens place.
Example: 47 will be rounded off to 50, but 83 will be rounded off to 80.
2. Rounding off to Hundreds
The same principle applies here. We see if the number is closer to the lower hundred or the higher one on the number line. We will better understand with examples.
Rounding off the numbers 416 and 485. Here 416 is definitely closer to 400, so we round it off to 400. And 485 will be rounded off to the next hundred, which is 500. One point to be noted, 450 while right in between 400 and 500 is generally rounded up to 500.
Example: Round off 43 to the nearest hundred. Here 43 is closer to 0 than to 100, and so we will round it off as 0.
3. Rounding off to Thousands
All numbers from 0 to 499 being closer to 0 on the number line will be rounded off as 0. Numbers from 500 to 999 will be rounded off as 1000. And the same principle will apply to all the larger numbers as well. The numbers closer to the lower thousand will be rounded down, and from 500 onwards will be rounded up.Example: Round off the following numbers
(i) 1234 → 1000
(ii) 7399 → 7000
(iii) 9845 → 10000
(iv) 3500 → 4000
Estimating Sums and Differences
Sometimes we don’t just estimate numbers, we all estimate certain mathematical productions. It makes calculating easier while giving us an estimation of the answer we require.
Example: You and your friends went on a donation drive. You each collected 435, 664, 410 and 239 rupees. So if you wanted to add up the amounts, an estimation of the sum would be efficient.
We will begin by rounding off the numbers to the nearest tens and then adding up the estimated numbers
(i) Estimated Sum: 440 + 660 + 410 + 240 = 1750
(ii) Actual Sum: 435 + 664+ 410 + 239 = 1748
As you can see from the calculations above the sums are very close to each other. The estimation of the sums was easier to calculate and time-saving as well. Let us now see some examples of estimation of differences and products.
Estimate: 5733 – 458
(i) If we round off to thousands, the answer will be:
5733 rounds off to 6000
458 rounds off to 0
This does not seem to be an accurate answer at all.
(ii) Now we round off to hundreds, the answer will be:
5733 rounds off to 5700
458 rounds off to 500
The difference is 5200, and this seems like an accurate and reasonable estimation.
Estimating Product of Numbers
- Round off each factor to its greatest place, then multiply the rounded off factors.
- Estimating the product of 199 and 31:
199 is rounded off to 200
31 is rounded off to 30
Estimated Product = 200 × 30 = 6000
Actual Result = 199 × 31 = 6169
Solved Example
Ques 1: Round-off 4353 to nearest 100.1. 4360
2. 4200
3. 4300
4. 4400
Ans: The correct answer is “D”.
4353 is closer to 4400 than 4300 on the number line.
Ques 2: (7268−2427) estimated to the nearest hundred is
1. 4800
2. 4900
3. 4841
4. 5000
Ans: The correct option is “A”.
We have (7268−2427) = 4841. Rounding off 4841 to the nearest hundred we get 4800.
ROMAN NUMERALS
Some basic Roman numerals are
 Few Roman numerals
Few Roman numerals
1→ I 10→X C→100
2→ II 20→XX D→500
3→ III 30→XXX M→1000
4→ IV 40→XL
5→ V 50→L
6→VI 60→LX
7→VII 70→LXX
8→VIII 80→LXXX
9→IX 90→XC
Rules of the Roman Numeral System
Roman numbers follow certain rules, which helps determine how the number is written. It will also help us in reading or recognizing roman numbers. Let us take a look.
- If a symbol is repeated, its value is added as many times as it occurs.
Example: II = 2, XX = 20 etc. - The symbols V, L and D are never repeated.
- A symbol is not repeated more than three times.
- If a smaller symbol is written to the right of a symbol with a greater value, then its value gets added to the value of the greater symbol.
Example: VI = 5+1 = 6, XI = 11 and so on. - If a smaller symbol is written on the left of a symbol with a greater value, then its value is subtracted from the value of the greater symbol.
Example: IV = 5-1 = 4, IX = 9 etc. - The symbols V, L and D are never written to the left of a symbol of greater value i.e. V, L and D are never subtracted. The symbol I can be subtracted from V and X only. The symbol X can be subtracted from L, M and C only.
- A symbol cannot be subtracted more than once from a particular symbol of greater value. In other words, we cannot repeat a symbol on the left side of a symbol. Eg, 98 is written as XCVIII and not as IIC.
Solved Examples
Ques 1: Convert the following numerals to the Roman numerals:
a. 69
b. 98
c. 109
d. 786
e. 1298
f. 2018
Ans: a. 69 = 60 + 9 = (50+10) + 9 = LX + IX = LXIX
b. 98 = 90+8 = (100-10) + 8 = XC + VIII = XCVIII
c. 109 = 100 + 9 = C + IX = CIX
d. 786 = 700 + 86 = (500 + 200) + ( 80 + 6) = DCC + LXXXVI = DCCLXXXVI
e. 1298 = (1000 + 200) + (90 + 8) = MCC + [(100-10) + 8)] = MCC + XCVIII = MCCXCVIII
f. 2018 = 2000 + 18 = MM + XVII= MMXVIII
Ques 2: Convert 1984 to Roman Numerals
Ans: We can write 1984 as 1000+900+80+4
Then 1000 = M
900 = CM
80 = LXXX
4 = IV
Hence, 1984 in Roman Letters is MCMLXXXIV
BODMAS Rule
Use of Brackets
First, we must understand the use of brackets in mathematics. It is a very important part of forming and solving equations. Let us take an example. You went to the store to buy chocolates. You went a little overboard and bought ten chocolates. Two of them cost Rs. 10/- each, seven of them were Rs 5/- each and one was for Rs 30/-. Now how will you represent this mathematically?
Well the equation will go something like this
2 × 10 + 5 × 7 + 1 × 30 = 85
However doesn’t the above equation seem very confusing? And if someone was asked to solve it he would be prone to errors and miscalculations. So let us conjure a better way of forming this equation using brackets.
(2 × 10) + (5 × 7) + (1 × 30) = 85
Doesn’t this make much more sense? It is an organized and systematic representation of the scenario. And the person solving the equation will have a better understanding as well. So you can see how the use of brackets is quite essential in mathematics.
BODMAS

Now moving on to the BODMAS rule. In the above equation, we saw that we were performing two operations, namely addition and multiplication. But imagine that in an equation you had to perform more such operations. It would be confusing. And which operation will you perform first? Take for example the following equation.
23 × 7 + 78 ÷ 2 = ?
So how do you solve such a problem? This is where the BODMAS rule comes in. It gives us an order in which to perform the mathematical operations in a given problem or equation.
It is actually an acronym and goes as follows
- B: Brackets
- O: Of
- D: Division
- M: Multiplication
- A: Addition
- S: Subtraction
This is the order in which you perform the operations to arrive at the correct answer. You first solve the operations within the bracket. This is called “opening the bracket’. Then you move on to division, after which you perform multiplication if the equation requires it from left to right. And finally, you add the numbers and lastly perform the subtraction.
The best way to understand the BODMAS rule is through examples. So let us see a few problems and solve them using BODMAS.
Solved Examples
Ques 1: Solve and find the value of x using the BODMAS rule.
42 ÷ 2 + x × 3 − 22 = 8
a. 2
b. 5
c. 4
d. 3
Sol: 42÷2+x×3−22 = 8
⇒ 21 + 3 × x = 8 +22 = 30 (Using BODMAS rule)
⇒ 3 × x =30 − 21 = 9
⇒ x = 9/3 = 3
Ques 2: Simplify 3+3 of 3÷3 of 3×3.
Sol: Applying the BODMAS rule,
3+3 of 3÷3 of 3×3
= 3+(3 of 3)÷3 of 3×3
= 3+9÷3 of 3×3
= 3+3 of 3×3
= 3+(3 of 3)×3
= 3+9×3
= 3+(9×3)
= 3+27 = 30
Ques 3: In the given equation find which of the following interchange of signs/numbers would make the equation correct 9 + 7 × 1= 5 − 3
a. + with –
b. + with ×
c. × with –
d. None of the above
Sol: The correct option is “C”.
We substitute × on the place of − and − on the place of × then the equation becomes correct
9 + 7 − 1 = 5 × 3
16 − 1 = 15
15 = 15
That is true.
|
75 videos|228 docs|70 tests
|
FAQs on Notes: Knowing our numbers - Mathematics & Pedagogy Paper 2 for CTET & TET Exams - CTET & State TET
| 1. What are the different components covered in the article "Knowing our numbers"? |  |
| 2. How can I understand the concept of place value better? |  |
| 3. What is the significance of Roman numerals in mathematics? |  |
| 4. Can you explain the BODMAS rule mentioned in the article? |  |
| 5. How can I improve my understanding of large numbers and their place value? |  |
|
75 videos|228 docs|70 tests
|

|
Explore Courses for CTET & State TET exam
|

|












