Notes: Linear Inequalities | Mathematics for ACT PDF Download
Linear Inequalities
In mathematics, inequality occurs when a non-equal comparison is made between two mathematical expressions or two numbers. In general, inequalities can be either numerical inequality or algebraic inequality or a combination of both. Linear inequalities are inequalities that involve at least one linear algebraic expression, that is, a polynomial of degree 1 is compared with another algebraic expression of degree less than or equal to 1. There are several ways to represent various kinds of linear inequalities.
What Are Linear Inequalities?
Linear inequalities are defined as expressions in which two linear expressions are compared using the inequality symbols. The five symbols that are used to represent the linear inequalities are listed below:
We need to note that if, p < q, then p is some number that is strictly less than q. If p ≤ q, then it means that p is some number that is either strictly less than q or is exactly equal to q. Likewise, the same applies to the remaining two inequalities > (greater than) and ≥ (greater than or equal to).
Now, Let's say we have a linear inequality, 3x - 4 < 20. In this case LHS < RHS. We can see that the expression on the left-hand side, that is, 3x - 4 is in fact lesser than the number on the right-hand side, which is 20. We can represent this inequality pictorially on a weighing scale as: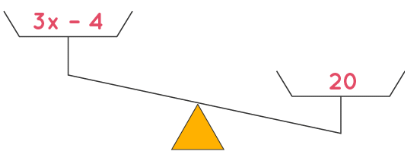
Rules of Linear Inequalities
The 4 types of operations that are done on linear inequalities are addition, subtraction, multiplication, and division. Linear inequalities with the same solution are called equivalent inequality. There are rules for both equality and inequality. All the rules mentioned below are also true for inequalities involving lesser than or equal to (≤), and greater than or equal to (≥). Before learning how to solve linear inequalities, let's look at some of the important rules of inequality for all these operations.
Addition Rule of Linear Inequalities:
As per the addition rule of linear inequalities, adding the same number to each side of the inequality produces an equivalent inequality, that is the inequality symbol does not change.
If x > y, then x + a > y + a and if x < y, then x + a < y + a.
Subtraction Rule of Linear Inequalities:
As per the subtraction rule of linear inequalities, subtracting the same number from each side of the inequality produces an equivalent inequality, that is the inequality symbol does not change.
If x > y, then x − a > y − a and if x < y, then x − a < y − a.
Multiplication Rule of Linear Inequalities:
As per the multiplication rule of linear inequalities, multiplication on both sides of an inequality with a positive number always produces an equivalent inequality, that is the inequality symbol does not change.
If x > y and a > 0, then x × a > y × a and if x < y and a > 0, then x × a < y × a, Here, × is used as the multiplication symbol.
On the other hand, multiplication on both sides of the inequality with a negative number does not produce an equivalent inequality unless we also reverse the direction of the inequality symbol.
If x > y and a < 0, then x × a < y × a and if x < y and a < 0, then x × a > y × a.
Division Rule of Linear Inequalities:
As per the division rule of linear inequalities, division of both sides of an inequality with a positive number produces an equivalent inequality, that is the inequality symbol does not change.
If x > y and a > 0, then (x/a) > (y/a) and if x < y and a > 0, then (x/a) < (y/a).
On the other hand, the division of both sides of an inequality with a negative number produces an equivalent inequality if the inequality symbol is reversed.
If x > y and a < 0, then (x/a) < (y/a) and if x < y and a < 0, then (x/a) > (y/a)
Solving System of Linear Inequalities
Solving linear inequalities in multi-step one variable is the same as solving multi-step linear equations; begin by isolating the variable from the constants. As per the rules of inequalities, while we are solving multi-step linear inequalities, it is important for us to not forget to reverse the inequality sign when multiplying or dividing with negative numbers.
- Step 1: Simplify the inequality on both sides - on LHS as well as RHS as per the rules of inequality.
- Step 2: When the value is obtained, if the inequality is a strict inequality, the solution for x is less than or greater than the value obtained as defined in the question. And, if the inequality is not a strict inequality, then the solution for x is less than or equal to or greater than or equal to the value obtained as defined in the question.
Now, let's try solving linear inequalities with an example, to understand the concept.
2x + 3 > 7
To solve this linear inequality, we would follow the below-given steps:
2x > 7 - 3 ⇒ 2x > 4 ⇒ x > 2
The solution to this inequality will be the set of all values of x for which this inequality x > 2 is satisfied, that is, all real numbers strictly greater than 2.
Solving Linear Inequalities with Variable on Both Sides
Let us try solving linear inequalities with one variable by applying the concept we learned. Consider the following example.
3x - 15 > 2x + 11
We proceed as follows:
-15 - 11 > 2x - 3x ⇒ - 26 > - x ⇒ x > 26
Solving System of Linear Inequalities by Graphing
The system of two-variable linear inequalities is of the form ax + by > c or ax + by ≤ c. The signs of inequalities can change as per the set of inequalities given. To solve a system of two-variable linear inequalities, we must have at least two inequalities. Now, to solve a system of linear inequalities in two variables, let us consider an example.
2y - x > 1 and y - 2x < -1
First, we will plot the given inequalities on the graph. To do that, follow the given steps:
- Replace the inequality sign with equal to =, that is, we have 2y - x = 1 and y - 2x = -1. Since the linear inequality is strict, we draw dotted lines on the graph.
- Check if the origin (0, 0) satisfies the given linear inequalities. If it does, then shade the region on one side of the line which includes the origin. If the origin does not satisfy the linear inequality, shade the region on one side side of the line which does not include the origin.
For 2y - x > 1, substitute (0, 0) we have: 2 × 0 - 0 > 1 ⇒ 0 > 1 which is not true. Hence, shade the side of the line 2y - x = 1 which does not include origin. Simillarly, for y - 2x < -1, substituting (0, 0), we have: 0 - 2 × 0 < -1 ⇒ 0 < -1 which is not true. Hence, hade the side of the line y - 2x = -1 which does not include origin. - The common shaded will be the feasible region that forms the solution of the system of linear inequalities. If there is no common shaded region, then the solution does not exist. The violet-colored region in the graph given below shows the solution of the given system of linear inequalities.
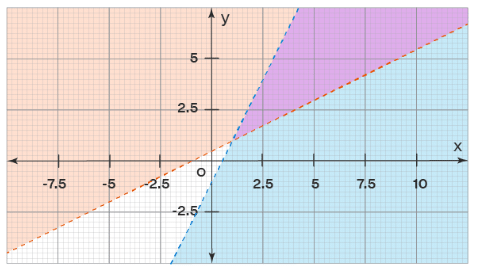
Graphing Linear Inequalities
Linear inequalities with one variable are plotted on a number line, as the output gives the solution of one variable. Hence, graphing linear inequalities in one variable is done using a number line only. On the contrary, linear inequalities with two variables are plotted on a two-dimensional x and y axis graph, as the output gives the solution of two variables. Hence, graphing of two-variable linear inequalities is done using a graph.
Graphing Linear Inequalities - One Variable
Let's consider the below example.
4x > -3x + 21
The solution in this case is simple.
4x + 3x > 21 ⇒ 7x > 21 ⇒ x > 3
This can be plotted on a number line as: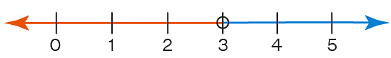
Any point lying on the blue part of the number line will satisfy this inequality. Note that in this case, we have drawn a hollow dot at point 3. This is to indicate that 3 is not a part of the solution set (this is because the given inequality has a strict inequality). As per the solution obtained, the blue part of the number line satisfies the inequality. Let's take another example of linear inequalities:
3x + 1 ≤ 7
We proceed as follows:
3x ≤ 7 - 1 ⇒ 3x ≤ 6 ⇒ x ≤ 2
We want to represent this solution set on a number line. Thus, we highlight that part of the number line lying to the left of 2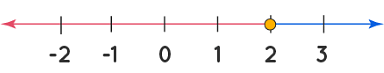 We see that any number lying on the red part of the number line will satisfy this inequality and so it is a part of the solution set for this inequality. Note that we have drawn a solid dot exactly at point 2. This is to indicate that 2 is also a part of the solution set.
We see that any number lying on the red part of the number line will satisfy this inequality and so it is a part of the solution set for this inequality. Note that we have drawn a solid dot exactly at point 2. This is to indicate that 2 is also a part of the solution set.
Important Notes on Linear Inequalities
Here is a list of a few points that should be remembered while studying linear inequalities:
- In the case of linear inequalities, some other relationship like less than or greater than exists between LHS and RHS.
- A linear inequality is called so due to the highest power(exponents) of the variable being 1.
- "Less than" and "greater than" are strict inequalities while "less than or equal to" and "greater than or equal to" are not strict linear inequalities.
- For every linear inequality which uses strict linear inequality, the value obtained for x is shown by a hollow dot. It shows that the value obtained is excluded.
- For every linear inequality which is not strict inequality, the value obtained for x is shown by a solid dot. It shows that the value obtained is included.
|
144 videos|100 docs|61 tests
|
FAQs on Notes: Linear Inequalities - Mathematics for ACT
| 1. What are linear inequalities? |  |
| 2. How are linear inequalities solved? |  |
| 3. What is the graphical representation of linear inequalities? |  |
| 4. How are linear inequalities used in real-life situations? |  |
| 5. Can linear inequalities have multiple solutions? |  |

|
Explore Courses for ACT exam
|

|

















