Notes: Maths Fun | GK Olympiad for Class 5 PDF Download
| Table of contents |

|
| Introduction |

|
| Place Value |

|
| Operations on numbers |

|
| Factors and Multiples |

|
| Money |

|
| Geometry |

|
Introduction

- Numbers play a crucial role in our daily lives.
- They are essential for various mathematical operations and help us understand concepts like time and money.
- Numbers can be represented in different forms such as fractions, decimals, bar graphs, and pie charts.
- Additionally, measurements of length, weight, and capacity are all expressed using numbers.
Number Sense
- Number sense refers to the ability to understand numbers, their sizes, and how to perform operations with two or more numbers.
- It involves various concepts such as ranking, comparisons, and grouping.
Place Value
- A place value chart is a useful tool for comprehending the system of numeration. It organizes numbers into different groups called periods.
- In the place value chart, commas are used to separate these periods for clarity.
Indian System of Numeration
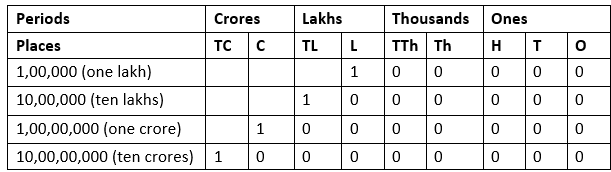
- The Indian system of numeration comprises four periods: Ones, Thousands, Lakhs, and Crores.
- Each period contains two place values, except for the Ones period, which has three place values.
- In this system, commas are placed after three digits from the right and then after every two digits towards the left to separate periods in a number.
International System of Numeration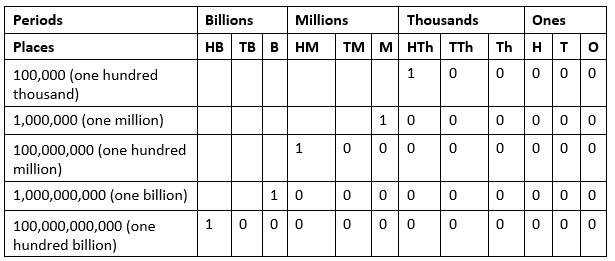
- The International system of numeration also consists of four periods: Ones, Thousands, Millions, and Billions.
- Each period in this system contains three place values.
- Commas are used after every three digits from the right to separate each period in a number.
Place, Place Value, and Face Value
- Each digit in a number occupies a specific position, known as its Place. The value of each digit depends on its place, which is called its Place Value.
- The Face Value of a digit is simply the value of the digit itself, regardless of its position. For instance, in the number 256482:
- Face Value of 6: 6
- Place Value of 6: 6 × 1000 = 6000
Expanded Form of a Number
- The expanded form of a number is the sum of the place values of its digits.
- For example, the expanded form of 2640923 is:2000000 + 600000 + 40000 + 0 + 900 + 20 + 3
Ordering Numbers
- Ascending Order: When numbers are arranged from the smallest to the biggest, they are in ascending (increasing) order.
- Descending Order: When numbers are arranged from the biggest to the smallest, they are in descending (decreasing) order.
- For example, given the numbers:39257344, 35082901, 35077172, 358172901, 358137344:
- Ascending Order: 35077172 < 35082901 < 39257344 < 358137344 < 358172901
- Descending Order: 358172901 < 358137344 < 39257344 < 35082901 < 35077172
Successor and Predecessor
- The Successor of a number is the number that comes right after it.
- The Predecessor of a number is the number that comes right before it.
- For example:
- Successor of 9999: 10000
- Predecessor of 9999: 9998
Roman Numerals
Roman numerals are a way of writing numbers using letters from the Roman alphabet. There are seven main symbols used in this system: I, V, X, L, C, D, and M.
Unlike the Hindu-Arabic numeral system we commonly use, Roman numerals do not have a place value system. Each symbol represents a specific value, and numbers are formed by combining these symbols according to certain rules.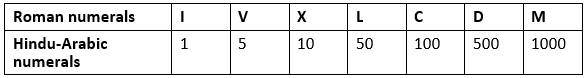
DID YOU KNOW?
There is no Roman number for ‘zero’ (0).
How Roman Numerals Work
Roman numerals are created by following specific rules. Let's explore these rules to understand how Roman numerals are formed:
Rule 1: Repeating Letters
- When a Roman numeral letter is repeated, its value is added together as many times as it is repeated.
- For example, the numeral XXX means 10 + 10 + 10, which equals 30.
Rule 2: Adding Smaller Value to Bigger Value
- When a letter of smaller value is written to the right of a letter with a bigger value, the smaller value is added to the bigger value.
- For example, in the numeral LX, 50 + 10 equals 60.
Rule 3: Subtracting Smaller Value from Bigger Value
- When a letter of smaller value is written to the left of a letter with a bigger value, the smaller value is subtracted from the bigger value.
- For example, in the numeral XC, 100 - 10 equals 90.
Rule 4: Smaller Value Between Two Bigger Values
- If a letter of smaller value is placed between two letters of bigger value, it is always subtracted from the letter on its right.
- For example, in the numeral XIV, it is calculated as 10 (5 - 1), which equals 10 4, resulting in 14.
Operations on numbers
Addition:
- Ordering Property: Changing the order of the numbers being added does not change the sum.
- Grouping Property: Changing the grouping of three or more numbers being added does not change the sum.
- Addition with 0: When 0 is added to any number, the result is the same number.
- Addition with 1: Adding 1 to any number gives the next whole number (successor) of that number.
Subtraction:
- Ordering Property: Changing the order of the numbers in subtraction changes the result.
- Subtraction by itself: Subtracting a number from itself always gives 0.
- Subtraction by 0: Subtracting 0 from a number gives the same number.
- Subtraction by 1: Subtracting 1 from a number gives the previous whole number (predecessor) of that number.
Multiplication:
- Ordering Property: Changing the order of the numbers being multiplied does not change the product.
- Grouping Property: Changing the grouping of three or more numbers being multiplied does not change the product.
- Multiplication by 0: Multiplying any number by 0 gives 0.
- Multiplication by 1: Multiplying any number by 1 gives the same number.
- Multiplication with numbers ending with 0: When multiplying by a number ending with 0, add one or more zeros to the end of the product.
- Distribution Property: When multiplying, if one number can be split into smaller numbers, especially with a multiple of 10, this property can be used.
Division:
- Ordering Property: Changing the order of the numbers in division changes the result.
- Division by itself: Dividing a number by itself gives 1.
- Division of 0: Dividing 0 by any number gives 0.
- Division by 1: Dividing a number by 1 gives the same number.
- Division by 10, 100, 1000: When dividing by 10, 100, or 1000, remove the last one, two, or three digits from the number to get the quotient.
Simplification:
To simplify problems with more than one operation, follow these steps:
- Solve the expressions inside the brackets first.
- Next, solve the 'of' operations.
- Then, tackle the division operations.
- After that, handle the multiplication operations.
- Next, perform the addition operations.
- Finally, carry out the subtraction operations.
These steps can be remembered with the acronym BODMAS, which stands for:
- B – Brackets (solve expressions in brackets first)
- O – Of (solve 'of' operations next)
- D – Division (handle division operations)
- M – Multiplication (carry out multiplication operations)
- A – Addition (perform addition operations)
- S – Subtraction (finally, perform subtraction operations)
Factors and Multiples
Factors are the numbers that are multiplied together to get a product. The product itself is called a multiple.
Properties of Factors:
- 1 is the smallest factor of every number.
- Every number, except zero, is the greatest factor of itself.
- A factor of a number is always less than or equal to that number.
- Every number, except 1, has at least two factors: 1 and the number itself.
- The factors of any number are limited (finite).
Properties of Multiples:
- Every number is a multiple of itself.
- Every number is a multiple of 1.
- Every multiple of a number is greater than or equal to the number itself.
- The first (or smallest) multiple of any number is the number itself.
- The multiples of any number are infinite.
- There is no greatest multiple of any number.
Divisibility Tests
- A number is divisible by 2 if its last digit is 0, 2, 4, 6, or 8.
- A number is divisible by 3 if the sum of its digits is divisible by 3.
- A number is divisible by 4 if the number formed by its last two digits is divisible by 4 or ends with '00'.
- A number is divisible by 5 if its last digit is 0 or 5.
- A number is divisible by 6 if it is divisible by both 2 and 3.
- A number is divisible by 7 if subtracting twice the last digit from the rest of the number gives a result that is either 0 or divisible by 7.
- A number is divisible by 8 if the number formed by its last three digits is divisible by 8 or ends with '000'.
- A number is divisible by 9 if the sum of its digits is divisible by 9.
- A number is divisible by 10 if its last digit is 0.
- A number is divisible by 11 if the difference between the sum of the digits in odd positions and the sum of the digits in even positions is either 0 or a multiple of 11.
- A number is divisible by 12 if it is divisible by both 2 and 6.
Even and Odd Numbers
- Even Numbers: Numbers that are divisible by 2.
- Odd Numbers: Numbers that are not divisible by 2.
Highest Common Factor and Lowest Common Multiple:
- The highest common factor (HCF) of two or more numbers is the largest factor that divides all of them exactly.
- The lowest common multiple (LCM) of two or more numbers is the smallest multiple that can be divided by all of them exactly.
Properties of HCF:
- The HCF is the greatest common factor of the numbers.
- The HCF cannot be greater than the numbers themselves.
- If one number is a factor of another, the smaller number is the HCF.
- The HCF of co-prime numbers is always 1.
Properties of LCM:
- The LCM is the smallest common multiple of the numbers.
- The LCM cannot be less than the numbers themselves.
- If one number is a multiple of another, the greater number is the LCM.
- The LCM of co-prime numbers is their product.
Relationship between HCF and LCM:
- The product of the HCF and LCM of two numbers is equal to the product of the numbers themselves:
- (HCF of a and b) × (LCM of a and b) = a × b
Fractions
- Fraction is used to represent a part of a whole.
- The fraction of shaded portion is 5/8and the fraction of the unshaded portion is 3/8.

Types of Fractions:
- Like Fractions: Fractions that have the same denominator. Example: 1⁄8, 3⁄8, 7⁄8
- Unlike Fractions: Fractions that have different denominators. Example: 1⁄4, 3⁄7, 7⁄15
- Proper Fractions: Fractions where the numerator is smaller than the denominator. Example: 1⁄8, 4⁄5, 11⁄17
- Improper Fractions: Fractions where the numerator is larger than the denominator. Example: 9⁄8, 11⁄5, 19⁄3
- Mixed Fractions: Fractions that include a whole number and a fraction. Example: 4 1⁄8, 9 3⁄11, 1 3⁄4
- Equivalent Fractions: Fractions that have the same value. Example: 1⁄2, 2⁄4, 3⁄6, 5⁄10
- Decimal Fractions: Fractions with denominators like 10, 100, or 1000. Example: 3⁄10, 5⁄100, 69⁄100
Comparing and Ordering Fractions:
- Like Fractions: In like fractions, the one with the larger numerator is greater.
- Unlike Fractions:
- Case 1: When fractions have the same numerator, the fraction with the larger denominator is smaller.
- Case 2: To compare unlike fractions, convert them into equivalent fractions by finding the least common denominator (LCM).
Decimals
Place Values of Decimals:
- Hundreds (100)
- Tens (10)
- Ones (1)
- Tenths (1/10 = 0.1)
- Hundredths (1/100 = 0.01)
- Thousandths (1/1000 = 0.001)
Types of Decimal Numbers:
Decimal numbers can be classified into three types based on their structure:
- Equivalent Decimals: These are decimal numbers that represent the same value even though they may have a different number of digits after the decimal point. For example, 0.5, 0.50, and 0.500 all represent the same value.
- Like Decimals: These decimal numbers have the same number of digits after the decimal point. For instance, 0.75 and 0.25 are like decimals because they both have two digits after the decimal.
- Unlike Decimals: Unlike decimals have a different number of digits after the decimal point. For example, 0.5 and 0.75 are unlike decimals because 0.5 has one digit after the decimal, while 0.75 has two.
Understanding Percent
- A percent is a way of expressing a number as a fraction of 100.
- The word "percent" comes from the Latin phrase "per centum," which means "by the hundred."
- In simpler terms, when we say a number is a certain percent, we mean it is that many parts out of 100.
- The symbol used for percent is "%."
- For example, 25% means 25 out of 100.
Percentage in Money and Measures:
- 1 paisa: 1 paisa is equal to 1% of a rupee. Since there are 100 paisas in a rupee, 1 paisa represents 1 out of 100 parts of a rupee.
- 1 centimeter (cm): 1 cm is equal to 1% of a meter. There are 100 centimeters in a meter, so 1 cm represents 1 out of 100 parts of a meter.
- 1 gram (g): 1 g is equal to 0.1% of a kilogram (kg). Since there are 1000 grams in a kilogram, 1 gram represents 1 out of 1000 parts, and 0.1% of a kg is equivalent to 1 g.
- 1 milliliter (ml): 1 ml is equal to 0.1% of a liter (l). There are 1000 milliliters in a liter, so 1 ml represents 1 out of 1000 parts, and 0.1% of a liter is equivalent to 1 ml.
- 1 meter (m): 1 m is equal to 0.1% of a kilometer (km). There are 1000 meters in a kilometer, so 1 m represents 1 out of 1000 parts, and 0.1% of a km is equivalent to 1 m.
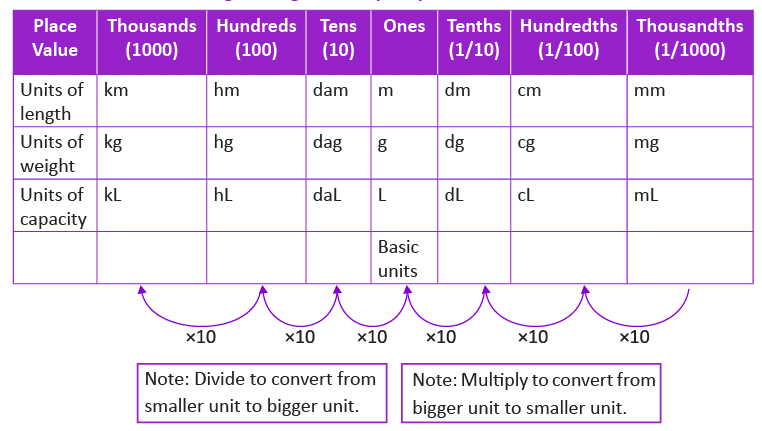
Length, weight and capacity
Money
Currency in India:
- Different countries around the world use different types of money called currencies.
- In India, the currency is called the Rupee, and it is used in the form of notes and coins.
Currency Notes in India:
- Currency notes are the paper money that people use for transactions.
- In India, the Reserve Bank of India (RBI) is responsible for issuing and regulating these currency notes.
- Currency notes come in different denominations, such as ₹10, ₹20, ₹50, ₹100, ₹200, ₹500, and ₹2,000.
- Each note has unique features, including images of important landmarks, famous personalities, and security measures to prevent counterfeiting.
- These notes are widely accepted for all kinds of transactions, from buying groceries to paying for services..

Coins in Circulation:
Profit and Loss
- Cost Price (CP): The price at which a shopkeeper buys an item.
- Selling Price (SP): The price at which the shopkeeper sells an item.
- When SP > CP, Profit = SP – CP and Profit Percentage = (Profit / CP) × 100
- When SP < CP, Loss = CP – SP and Loss Percentage = (Loss / CP) × 100
Time
- 1 year = 365 days
- 1 year = 12 months
- 1 week = 7 days
- 1 day = 24 hours
- 1 hour = 60 minutes
- 1 minute = 60 seconds
Conversion of units of time:
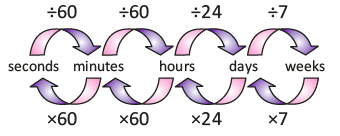
- a.m. (ante meridian): Used for times after midnight up to noon.
- p.m. (post meridian): Used for times after noon up to midnight.
Geometry
- Plane: A flat surface extending in all directions.
- Point: Represents a location with no dimensions.
- Line: A straight path with no endpoints, symbolized as ‘—’.
- Ray: A part of a line that extends indefinitely in one direction.
- Line Segment: A measurable part of a line with two endpoints.
- Collinear Points: Points lying on the same line.
- Non-collinear points: Three or more points not lying on the same line are called non-collinear points.
- Intersecting Lines: Two lines that meet at a common point.
- Parallel Lines: Lines that never meet.
- Perpendicular Lines: Lines that meet at right angles.
- Concurrent lines: Three or more lines meeting each other at the same point are called concurrent lines. This common point is called ‘the point of concurrence’.
- Coplanar lines: Lines that lie in the same plane are called coplanar lines.
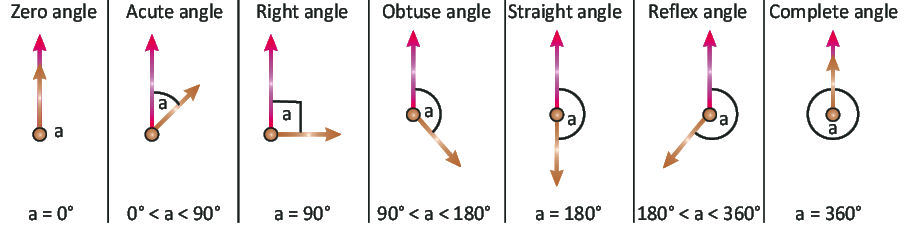
Angles
- Zero Angle: 0°
- Acute Angle: Less than 90°
- Right Angle: Exactly 90°
- Obtuse Angle: Greater than 90° but less than 180°
- Straight Angle: Exactly 180°
- Complete Angle: Exactly 360°
- Reflex Angle: Greater than 180° but less than 360°
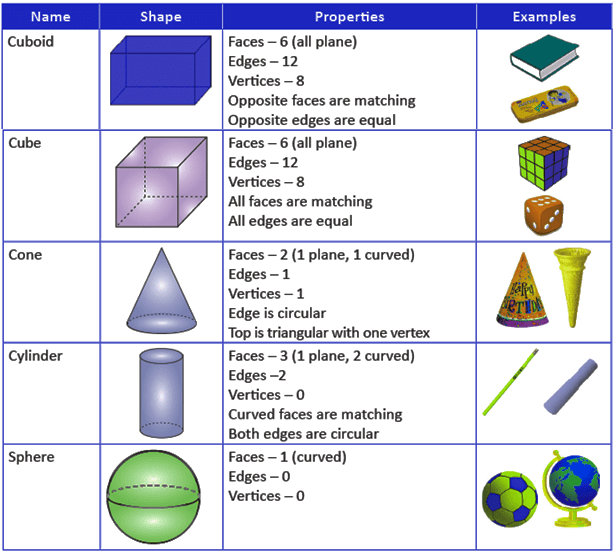
Shapes and Their Properties

Symmetry
- When a shape is divided into two equal parts, they look like mirror images. This is called symmetry.

- Symmetry exists in 3D shapes too, and some shapes have more than one line of symmetry.
Reflectional Symmetry:
- Reflectional symmetry is when a figure can be divided into two identical parts by a line. This line is called the line of symmetry.
- One part of the figure is a mirror image of the other part, just like how you see your reflection in a mirror.
- The two parts on either side of the line of symmetry look exactly the same, but one is a reflection of the other.

Perimeter and Area
- Area: The surface covered by a shape (e.g., in square cm, square m).
- Perimeter: The total length of the boundary of a shape.
- Square: Area = Side × Side, Perimeter = 4 × Side
- Rectangle: Area = Length × Breadth, Perimeter = 2 × (Length + Breadth)
- Triangle: Perimeter = Side1 + Side2 + Side3
Data Handling
- Bar Graph: A graphical representation of data using bars.
- Circle Graph (Pie Chart): Represents data in sectors of a circle.
- Tally Chart: Represents frequencies using tally marks.

- Line Graph: Represents changes over time using lines.

Fun Trivia
- Think of a number. Double it. Add 6. Half it. Subtract the number you started with. Your answer will be 3.
- Sunflower seeds follow the Fibonacci sequence in nature.
|
8 videos|19 docs|27 tests
|
FAQs on Notes: Maths Fun - GK Olympiad for Class 5
| 1. What are even and odd numbers? |  |
| 2. How do you find the Highest Common Factor (HCF) and Lowest Common Multiple (LCM) of two numbers? |  |
| 3. What are fractions and how do you add or subtract them? |  |
| 4. What is the difference between decimals and fractions? |  |
| 5. How do you calculate profit and loss in a business transaction? |  |














