Notes: Measurement | Mathematics & Pedagogy Paper 1 for CTET & TET Exams - CTET & State TET PDF Download
| Table of contents |

|
| Units of Measurement |

|
| Measurement of Length |

|
| Measurement of Mass(Weight) |

|
| Measurement of Capacity |

|
| Estimate in Measures |

|
| Finding Fractions of Quantities |

|
Measurement is a crucial concept in mathematics that involves quantifying attributes of objects and events. It is an essential topic for the Central Teacher Eligibility Test (CTET) and state-level Teacher Eligibility Tests (TETs) as it lays the foundation for understanding units, conversions, and real-world applications.

Types of Measurement
Length: The distance between two points. Units include meters (m), centimeters (cm), and kilometers (km).
Mass: The amount of matter in an object. Units include grams (g) and kilograms (kg).
Capacity: The amount a container can hold. Units include milliliters (ml) and liters (l).
Time: The duration between events. Units include seconds (s), minutes (min), hours (h), days, weeks, months, and years.
Area: The amount of space inside a shape. Units include square meters (m²) and square centimeters (cm²).
Volume: The amount of space an object occupies. Units include cubic meters (m³) and cubic centimeters (cm³).
Units of Measurement
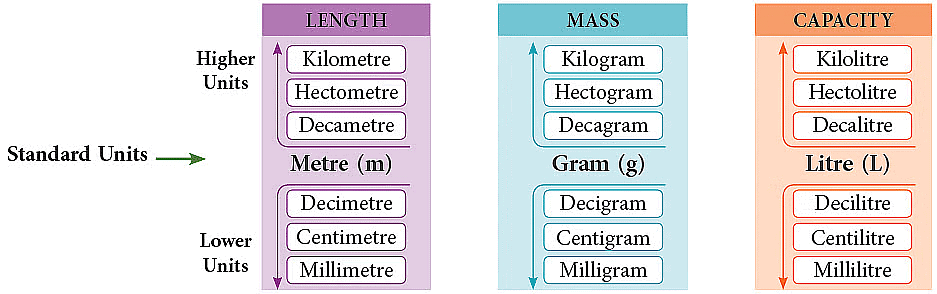
- The metric system is a way of measuring things using numbers that are multiples of 10.
- It has standard units for length (meter), mass (gram), and capacity (liter).
- A visual representation of the standard units of length, mass and capacity has been shown :

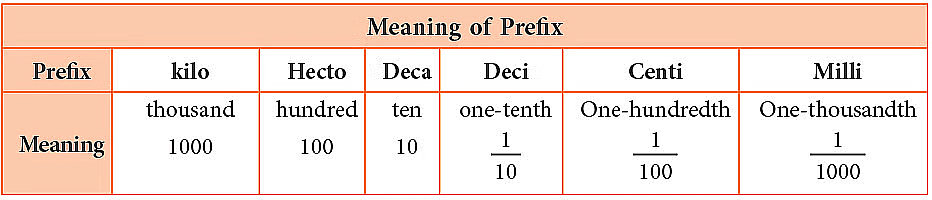
- Sometimes these units are too small or too big for what we need to measure.
- To fix this, we use prefixes with the standard units to make bigger or smaller units as shown in the figure below:

- For example, "kilo" means 1000, so a kilometer is 1000 meters.
- And "milli" means 1/1000, so a milliliter is 1/1000 of a liter, which is really tiny.
- This helps us measure things like long distances, small amounts of liquid, or big weights more easily.
Measurement of Length
- Different units are used to measure length, like kilometers, meters, centimeters, and millimeters.
- Kilometers are for really long distances, like between cities.
- Meters are the standard unit for measuring things like the length of a room or the height of a person.

- Centimeters are used for shorter lengths, like the width of a book.
- Millimeters are even smaller, for really tiny measurements, like the thickness of a coin.
The chart given below shows the units of length in the metric system with metre as the reference unit. This shows that the metric system is like the decimal system.
This shows that the metric system is like the decimal system.
Relation between different units of length
This chart will help you convert bigger units into smaller units and smaller units into bigger units.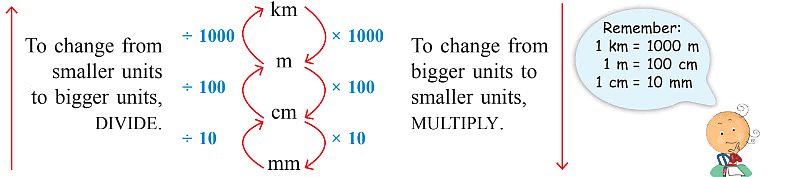
The following diagram shows how to carry out these conversions.
Rule:
- Moving from left to right, you multiply by 10 at each step. Move one step right, multiply by 10, move two steps right, multiply by 10 × 10 = 100 and so on.
- Moving from right to left, you divide by 10 at each step. Move one step left, divide by 10, move two steps left, divide by 100 and so on.
Solved Examples
Example 1: Convert the following bigger units to smaller units.
- 3 km = (3 × 1000) m = 3000 m
- 8 hm = (8 × 100) m = 800 m
- 5 m = (5 × 100) cm = 500 cm
- 1.03 m = (1.03 × 1000) mm = 1030 mm
Example 2: Convert the following smaller units to bigger units.
- 8400 m = (8400 ÷ 1000) km = 8.4 km
- 370 m = (370 ÷ 100) hm = 3.7 hm
- 2000 mm = (2000 ÷ 1000) m = 2 m
- 73 cm = (73 ÷ 100) m = 0.73 m
Example 3: Convert as directed.
(a) 60 mm to cm
(b) 720 dam to km
(c) 85 hm to km
(d) 7340 dm to hm
(e) 12000 cm to dam
Sol: (a) 60 mm = (60 ÷ 10) cm = 6 cm
cm is one step to the left of mm, so divide by 10.
(b) 720 dam = (720 ÷ 100) km = 7.2 km
km is two steps to the left of dam, so divide by 100.
(c) 85 hm = (85 ÷ 10) km = 8.5 km
km is one step to the left of hm, so divide by 10.
(d) 7340 dm = (7340 ÷ 1000) hm = 7.340 hm
hm is three steps to the left of dm, so divide by 1000.
(e) 12000 cm = (12000 ÷ 1000) dam = 12 dam
dam is three steps to the left of cm, so divide by 1000.
Using decimals to express length
- Decimals help us express lengths using smaller units.
- For example, if Rini's dad travels 7 kilometers and 500 meters, we can write it as 7500 meters.

- Using decimals, we can also write it as 7.500 kilometers.
- So, 7 kilometers and 500 meters is the same as 7.500 kilometers when we use decimals.
Solved Examples
Example 1: There was 2.1 cm rainfall on Monday.How much is that in mm?
Sol: 2.1 × 10 = 21 mm
The rainfall on Monday was 21 mm.
Example 2: My mother is 153 cm tall. How much will that be in m?
Sol: 153 ÷ 100 = 100
153 = 1.53 m
My mother is 1.53 m tall.
Example 3: The wheel of a bicycle covers a distance of 2 m in 1 revolution. How much distance would it cover in 600 revolutions? Write your answer in km.
Sol: Distance covered in 600 revolutions = 2 × 600 = 1200 m
1200 m ÷ 1000m = 1200/1000 = 1.2 km
The wheel would cover 1.2 km in 600 revolutions.
Measurement of Mass(Weight)
- The amount of matter in an object is its mass.
- We use different units to measure weight, like kilograms, grams, and milligrams.
- Kilograms are for heavy things, like people or bags of flour.
- Grams are the standard unit for measuring weight, used for lighter things like apples or pencils.
- Milligrams are for very light things, like tiny grains of salt or medicine doses.
The chart given below shows the units of mass in the metric system with gram as the reference unit.
Relation between different units of Mass

This chart will help you convert bigger units into smaller units and smaller units into bigger units.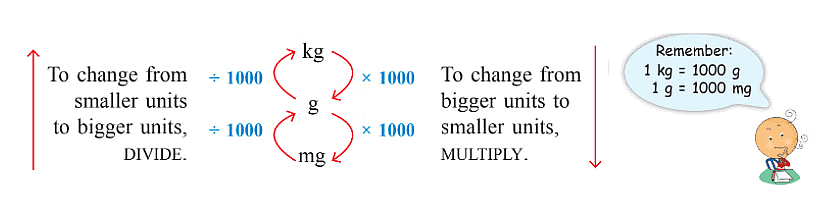
Using Decimals to Express Mass (Weight)
- Decimals help us show weight using bigger units.
- For example, if Rini's mom buys tomatoes weighing 1 kilogram and 750 grams, we can write it as 1750 grams.

- Using decimals, we can also write it as 1.750 kilograms.
- So, 1 kilogram and 750 grams is the same as 1.750 kilograms when we use decimals
Solved Examples
Example 1: Conversion of various units to grams and vice versa.
(i) 24 kg = (24 × 1000) g = 24000 g
(ii) 1.217 g = (1.217 × 1000) mg = 1217 mg
(iii) 3200 mg = (3200 ÷ 1000) g = 3.2 g
(iv) 315 cg = (315 ÷ 100) g = 3.15 g
Example 2: Conversion between Units
(i) 14 mg = (14 ÷ 10) cg = 1.4 cg (ii) 300 dg = (300 ÷ 100) dag = 3 dag
(ii) 300 dg = (300 ÷ 100) dag = 3 dag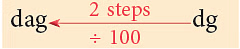
(iii) 2417 cg = (2417 ÷ 1000) dag = 2.417 dag
(iv) 38 kg = (38 × 100) dag = 3800 dag
(v) 23.7 dg = (23.7 × 10) cg = 237 cg
(vi) 4 hg = (4 × 1000) dg = 4000 dg
Example 3: A basket of apples weighs 2.5 kg. How much is that in g?
Sol: 2.5 × 1000 = 2500 g
The basket of apples weighs 2500 g.
Measurement of Capacity
- We use different units to measure how much liquid something can hold, like liters and milliliters.
- Liters are the standard unit for measuring liquid, like how much water is in a jug.

- Milliliters are smaller than liters and are used for measuring small amounts of liquid, like medicine in a syringe.
The chart given below shows the units of capacity in the metric system with litre as the reference unit.
Relation between different units of Capacity

This chart will help you convert bigger units into smaller units and smaller units into bigger units.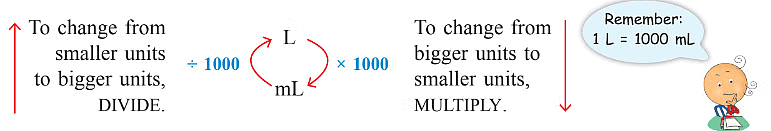
Using Decimals to express Capacity
- Decimals help us show how much liquid something can hold using bigger units.
- For example, if Rini's brother made 1 liter and 200 milliliters of lemonade, we can write it as 1200 milliliters.
- Using decimals, we can also write it as 1.200 liters.
- So, 1 liter and 200 milliliters is the same as 1.200 liters when we use decimals.
Solved Examples
Example 1: Conversion of various units to litres and litres to various units
(i) 2.3 kL = (2.3 × 1000) L = 2300 L
(ii) 1.8 cL = (1.8 ÷ 100) L = 0.018 L
(iii) 64 hL = (64 × 100) L = 6400 L
(iv) 600 L = (600 ÷ 100) hL = 6 hL
(v) 7315 mL = (7315 ÷ 1000) L = 7.315 L
(vi) 11.9 L = (11.9 × 1000) mL = 11900 mL
Example 2: Conversions between Units.
(i) 25 hL = (25 × 10) daL = 250 daL
(ii) 13.8 dL = (13.8 × 100) mL = 1380 mL
(iii) 500 daL = (500 ÷ 100) kL = 5 kL
(iv) 3.117 hL = (3.117 × 1000) dL = 3117 dL
The Four Basic Operations on Metric Measures
Addition and Subtraction
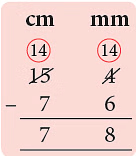
Example 1: Ritu drew a line segment of length 15 cm 4 mm. Then, she erased a portion of it. The remaining line segment measured 7 cm 6 mm. What is the length in mm of the erased line segment?
Sol: Length of the line segment in the beginning = 15 cm 4 mm
Length of line segment left after erasing = 7 cm 6 mm
Length of line segment erased = 15 cm 4 mm – 7 cm 6 mm
= 7 cm 8 m m
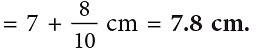
Example 2: Add:
(a) 3 cm 4 mm and 9 cm 8 mm
(b) 14 dm 4 cm and 23 dm 7 cm
(c) 53 kg 305 g and 7 kg 828 g
(d) 8 L 718 mL and 7 L 732 mL
Sol: (a)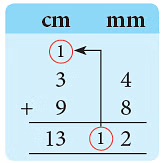 12 mm= 10 mm + 2 mm= 1 cm + 2 mm
12 mm= 10 mm + 2 mm= 1 cm + 2 mm
= 13 cm 2 mm = 13.2 cm.
(b) 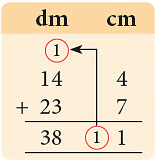 11 cm= 10 cm + 1 cm= 1 dm + 1 cm
11 cm= 10 cm + 1 cm= 1 dm + 1 cm
= 38 dm 1 cm = 38.1 dm.
(c)  1133 g= 1000 g + 133 g= 1 kg + 133 g
1133 g= 1000 g + 133 g= 1 kg + 133 g
= 61 kg 133 g = 61.133 kg.
(d)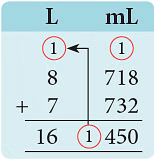 1450 mL= 1000 mL + 450 mL= 1 L + 450 mL
1450 mL= 1000 mL + 450 mL= 1 L + 450 mL
= 16 L 450 mL = 16.450 L.
Example 3: Subtract:
(a) 10 m 36 cm – 5 m 83 cm
(b) 28 cm 4 mm – 13 cm 8 mm
(c) 40 kg 353 g – 17 kg 500 g
(d) 8 kL 150 L – 4 kL 850 L
Sol: (a)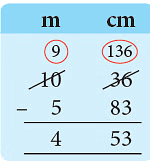 36 cm < 83 cmBorrow 1 m = 100 cm100 cm + 36 cm
36 cm < 83 cmBorrow 1 m = 100 cm100 cm + 36 cm
= 136 cm
= 4.53 m.
(b)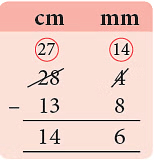 4 mm < 8 mm
4 mm < 8 mm
Borrow 1 cm = 10 mm
10 mm + 4 mm
= 14 mm
= 14.6 cm.
(c)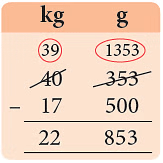 353 g < 500 gBorrow 1 kg = 1000 g1000 g + 353 g
353 g < 500 gBorrow 1 kg = 1000 g1000 g + 353 g
= 1353 g
= 22.853 kg.
(d)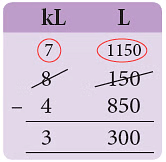 150 L < 850 LBorrow 1 kL = 1000 L1000 L + 150 L
150 L < 850 LBorrow 1 kL = 1000 L1000 L + 150 L
= 1150 L
= 3.300 kL.
Multiplication
Arrange numbers in columns unitwise and then multiply as you would multiply whole numbers.
Example 4: Find, in centimetres, the height of a pile of 25 books, if each book is 3 cm, 5 mm thick.
Sol: Thickness of 1 book = 3 cm 5 mm = 3.5 cm
Height of 25 books = 3.5 cm × 25
= 87.5 cm
Thus, height of the pile of 25 books
= 87.5 cm.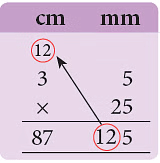
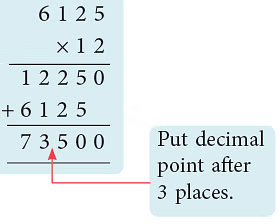
Example 5: A carton full of fruits weighs 6 kg 125 g. What is the weight of 12 such cartons in kg?Sol: Weight of one carton = 6 kg 125 g
= 6.125 kg
∴ Weight of 12 cartons = (6.125 × 12) kg
= 73.500 kg
= 73 kg 500 g.
Division
In division also arrange the numbers in columns unitwise and then divide like whole numbers.
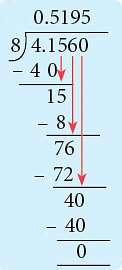
Example 6: Reena prepared 4 L 156 mL of orange juice. Distribute it equally among 8 children. How many mL of orange juice each child gets?
Sol: Juice Reena prepared = 4 L 156 mL = 4.156 L
When distributed among 8 children,
juice each child gets = (4.156 ÷ 8) L
= 0.51 95 L
= 519 .5 mL.
Example 7: How many 150 mL glasses can I fill with 5 bottles of soft drinks each holding 1.2 litres?
Sol: Total soft drink in 5 bottles = 1.2 L × 5 = 6.0 = 6 L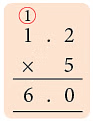 ∵ 1 L = 1000 mLTotal soft drink = 6 L = 6 × 1000 = 6000 mLNumber of 150 mL of glasses that can be filled = 6000 mL ÷ 150 mL = 40
∵ 1 L = 1000 mLTotal soft drink = 6 L = 6 × 1000 = 6000 mLNumber of 150 mL of glasses that can be filled = 6000 mL ÷ 150 mL = 40
Thus, with 6 L of soft drink, I can fill 40 glasses of 150 mL.
Estimate in Measures
You cannot always be exact in measures. In our day-to-day life, we estimate the measures. To be able to estimate measures correctly, you should have a fair idea of how to relate commonplace things with the commonly used units of measures.
Length
- For long lengths or distances, we use kilometres (km) as unit.
 Length of India = 3214 km Breadth of India = 2933 km
Length of India = 3214 km Breadth of India = 2933 km - For medium lengths, we use metres (m).
 The length of your dining table.
The length of your dining table. - For short lengths, we use centimetres (cm).
 Length of a small ruler = 15 cm.
Length of a small ruler = 15 cm. - For very short lengths, we use millimetres (mm).
 The tip of your pencil = 2 mm.
The tip of your pencil = 2 mm.
Mass
- For very large masses, we use tonne (t) and quintal (q).
 Truck = 4 tonne, Sack of rice = 1 quintal.
Truck = 4 tonne, Sack of rice = 1 quintal. - For medium masses, we use kilograms (kg).
 The weight of your school bag = 5 kg.
The weight of your school bag = 5 kg. - For small masses, we use grams (g).
 An orange is about 100 g.
An orange is about 100 g. - For very small masses, we use milligrams (mg).
 A teaspoon of salt = 5 mg.
A teaspoon of salt = 5 mg.
Capacity
- For large capacities, we use kilolitre.
 Capacity of a swimming pool = 600 kL.
Capacity of a swimming pool = 600 kL. - For medium capacities, we use litres.
 A bathing bucket = 20 L.
A bathing bucket = 20 L. - For small capacities, we use millilitres.
 A bottle of medicine = 200 mL.
A bottle of medicine = 200 mL.
Finding Fractions of Quantities
Example 8: A basket contains 3 kg 705 g of mangoes. 23 of the mangoes are eaten by Mr Bhasin. Lata, his daughter, gets 25 of the remaining mangoes. What is her share in grams?
Sol: Total weight of mangoes = 3 kg 705 g
Mangoes eaten by Mr Bhasin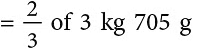
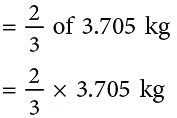
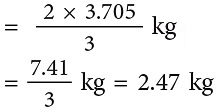
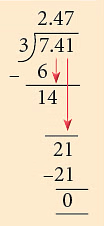 Mangoes left = 3.705 kg – 2.47 kg= 1.235 kgMangoes eaten by Lata
Mangoes left = 3.705 kg – 2.47 kg= 1.235 kgMangoes eaten by Lata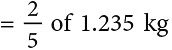
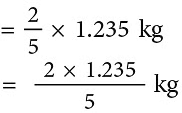
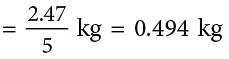 = (0.494 × 1000) g= 494 g
= (0.494 × 1000) g= 494 g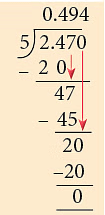 So, Lata ate 494 g of the mangoes.
So, Lata ate 494 g of the mangoes.
Example 9: Anshul had 45 kg of wafers. He packed all the wafers equally into 5 small packets. How many grams of wafers were there in each packet?
Sol: Total wafers with Anshul = 4 / 5 kg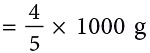 = 800 g800 g wafers are filled in 5 small packets.
= 800 g800 g wafers are filled in 5 small packets.
∴ Wafers in one packet = 800 ÷ 5
= 800 / 5 = 160 g
So, each packet contains 160 g of wafers.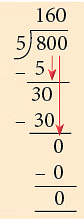
Example 15: Madhuri drew a line segment of length 20 cm 5 mm. She accidentally erased 2 / 5 of it. What is the length of the remaining line segment in cm?
Sol: Length of the line segment drawn = 20 cm 5 mm = 20.5 cm
Length of the erased line segment = 2 / 5 of 20.5 cm
= (2 × 4.1) cm
= 8.2 cm
Length of the remaining line segment = 20.5 cm – 8.2 cm
= 12.3 cm.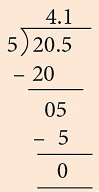
|
41 videos|151 docs|72 tests
|
FAQs on Notes: Measurement - Mathematics & Pedagogy Paper 1 for CTET & TET Exams - CTET & State TET
| 1. What are the common units of measurement for length? |  |
| 2. How is mass or weight typically measured? |  |
| 3. What units are used to measure capacity or volume? |  |
| 4. How can you estimate measurements in different units? |  |
| 5. How can fractions be used to find parts of a quantity in measurement? |  |
|
41 videos|151 docs|72 tests
|

|
Explore Courses for CTET & State TET exam
|

|