Notes: Numbers | Mathematics & Pedagogy Paper 1 for CTET & TET Exams - CTET & State TET PDF Download
Understanding numbers is fundamental to mathematical proficiency, especially for those preparing for the Central Teacher Eligibility Test (CTET) and state-level Teacher Eligibility Tests (TETs). These exams frequently test candidates' numerical abilities, with questions on various aspects of numbers. Here are some key topics:
Numeration System
The numeration system is the method used to represent numbers. The most commonly used system is the decimal system, which is a base-10 system. It uses ten digits, from 0 to 9, to represent all numbers. Each digit's place value is a power of 10, which makes it easy to understand and use.
 dxsc
dxsc
Counting 3 Digit Numbers
Three-digit numbers in terms of hundreds can be written as:
- 10 tens = 100 or 1 hundred
- 20 tens = 200 or 2 hundreds
- 30 tens = 300 or 3 hundreds
- 40 tens = 400 or 4 hundreds
- 50 tens = 500 or 5 hundreds
- 60 tens = 600 or 6 hundreds
- 70 tens = 700 or 7 hundreds
- 80 tens = 800 or 8 hundreds
- 90 tens = 900 or 9 hundreds
- 100 tens = 1000 or 10 hundreds = 1 thousand
Do you know?
- 1000 is the smallest 4-digit number.
- 999 is the largest 3-digit number.
- 100 is the smallest 3-digit number.
- 99 is the largest 2-digit number.
Place Value of a Number
The place value of a digit depends on the position of the digit in the place value chart:

- The place value of 4 is 4 hundred or 400.
- The place value of 6 is 6 tens or 60.
- The place value of 9 is 9 ones or 9.
Face Value of a Number
In a numeral, the face value of a digit is the actual value of the digit, at whatever places it may be.
Thus, in the numeral 569,
- the face value of 5 is 5;
- the face value of 6 is 6;
- the face value of 9 is 9.
Expanded Form of Numbers
To express a number as a sum of place values of its digits is called expanded form.
In the numeral 29,


Comparison of Three-Digit Numbers
To compare 3-digit numbers, first we compare the digits at the hundreds place and then tens place and at last the ones place.
Let us compare the numbers 528 and 536.
Which one is lesser?

Here digits at hundreds places in both the numbers are same. So, we compare tens place digits of both numbers.
Since 2 < 3
So, 528 < 536.
We say that 528 is less than 536.
Let us now compare 782 and 789. Which one is greater?

Digits at hundreds and tens places in both the numbers are same. So, we compare digits at ones place.
Since 9 > 2
So, 789 > 782.
We say that 789 is greater than 782.
Note: A one-digit number < a two-digit number < a three-digit number.
Ascending and Descending Order
Ascending order: Ascending is increasing (i.e., small → big).
Example: Arrange these numbers in ascending order (i.e., smallest to greatest).
498, 567, 834, 715
In the above numbers, the smallest number is 498 and the greatest number is 834.
Ascending order is: 498, 567, 715, 834
or
498 < 567 < 715 < 834
Descending order: Descending is decreasing (i.e., big → small).
Example: Arrange these numbers in descending order (i.e., biggest → smallest).
826, 736, 582, 914
In the above numbers, the largest number is 914 and the smallest number is 582.
Descending order is: 914, 826, 736, 582
or
914 > 826 > 736 > 582
Even and Odd Numbers
Even numbers
Let us take a collection of 6 apples. Group these apples into pairs (i.e., set of 2 apples each).
Group these apples into pairs (i.e., set of 2 apples each).
Is there any apple left? No.
So, 6 can be fully grouped into pairs. Such numbers which can be fully grouped into pairs are called even numbers.
Note: Even numbers have 0, 2, 4, 6 or 8 at ones place.
Odd numbers
Let us take a collection of 7 oranges. Group these oranges into pairs (i.e., set of 2 oranges each).
Group these oranges into pairs (i.e., set of 2 oranges each). Is there any orange left? Yes, one.So, 7 cannot be fully grouped into pairs.Such numbers which cannot be fully grouped into pairs are called odd numbers.
Is there any orange left? Yes, one.So, 7 cannot be fully grouped into pairs.Such numbers which cannot be fully grouped into pairs are called odd numbers.
Note: Odd numbers have 1, 3, 5, 7 or 9 at ones place.
Numerals are like special symbols we use to write numbers, like 1, 2, 3. When we write numbers using words instead of symbols, it's called numeration. A number system is just a way of organizing these symbols or words to represent numbers.

What is Numeration?
Numeration is the process of using symbols, like numerals, to represent numbers. When we express a number using words, it's called numeration. Numeration systems are structured methods for counting and determining the total quantity in a collection.
Numerical systems serve three main purposes: identification, ordering, and counting. For example, in a race, these systems help determine the positions of participants, such as first, second, or third place, by identifying their order in the series
 Numeration with Abacus
Numeration with Abacus
At the time of Independence, India had 23,444 post offices all over the country. Today, we have more than 1,55,618 post offices. Can you read the above numbers?
Number System defines a set of values used to represent a quantity. A number is used in counting and measuring quantities. There are two types of number systems:
- International Number System
- Indian Number System
How to Read and Write 5-Digit Numbers?
We know that 9,999 is the largest 4-digit number. If we add 1 to it, we get 10,000, which is the smallest 5-digit number.
- This also leads to a new place called the ten thousands place. 10,000 is read as ten thousand.
Look at the following books:
- There are 10 books with 1,000 pages in each book.
- We say that there are 10 thousand = 1 ten thousand = 10,000 pages in all.
- Thus, 10 thousands = 1 ten thousand = 10,000.
- The following abacus will help you to understand the above:

Instructions to Follow
1. Count by Ten thousands
2. Forming 5-Digit Numbers
- If we add 1 to the smallest 5-digit number, 10,000, we get
10,000 + 1 = 10,001 (which is read as ten thousand one). - If we add 1 to 10,001, we get 10,001 + 1 = 10,002 (which is read as ten thousand two)
- 99,998 + 1 = 99,999 (which is read as ninety-nine thousand nine hundred ninety-nine).
- 99,999 is the greatest 5-digit number.
- If we add 1 to this number, we get 99,999 + 1 = 1,00,000 which is read as 100 thousands or 1 lakh.
This number has 6 digits. - 1,00,000 is the smallest 6-digit number.
Edurev Tips:
- Ones Period: Ones, Tens, Hundreds
- Thousands Period: Thousands, Ten Thousands
3. Writing 5-Digit Numbers
- We split up a large number into groups or periods starting from the right to make it easy to read and write.
- For a 5-digit number, the first three places from the right make the ones period and the next two make the thousands period. We separate the periods using commas or leave a short space.
- Thus, the number 18730 can be written as 18,730 or 18 730.
4. Reading 5-Digit Numbers
- While reading a number, all the digits in the same period are read together and the name of the period (except the ones) is read with the digits.
- Let us read the number 36,207.
- We arrange the digits of given number in the place value chart, as shown below.
 We have, 36,207 = Thirty-six thousand two hundred seven.Similarly, 50,327 = Fifty thousand three hundred twenty-seven.
We have, 36,207 = Thirty-six thousand two hundred seven.Similarly, 50,327 = Fifty thousand three hundred twenty-seven. - We can represent the above numbers on the abacus, as shown below:

How to Read and Write 6-Digit Numbers?
To write the smallest 6-digit number, 1 lakh or 100000 using commas, we proceed as under:
- Starting from the right, we put a comma after three digits and then another comma after the fifth digit.
 We represent the smallest 6-digit number 1,00,000, in the Indian place value chart, as shown below:
We represent the smallest 6-digit number 1,00,000, in the Indian place value chart, as shown below: 1 is in the lakhs place. So, 1,00,000 is read as 1 lakh.
1 is in the lakhs place. So, 1,00,000 is read as 1 lakh.
Instructions to Follow
1. Counting in Lakhs
2. Forming 6-Digit Numbers
- 6-digit numbers beyond 1,00,000 can be formed as follows.
1,00,000 + 1 = 1,00,001 (One lakh one);
1,00,001 + 1 = 1,00,002 (One lakh two);
1,11,110 + 1 = 1,11,111 (One lakh eleven thousand one hundred eleven),…,
9,99,998 + 1 = 9,99,999 (Nine lakh ninety-nine thousand nine hundred ninety-nine);
9,99,999 is the greatest 6-digit number. - In a 6-digit number, the first three places from the right make the ones period, the next two make the thousands period and the next, that is, the sixth place, makes the lakhs period.
- We may put a comma between different periods or leave space between them. Thus, ‘four lakh’ may be written as 4,00,000 or 4 00 000.
3. Representing 6-Digit Numbers on Abacus
- We can represent 6-digit numbers on the abacus, as follows.

- The abacuses shown above represent the numbers 1,00,001 and 3,48,726 and 7,03,189, respectively.
- They are read as one lakh one; three lakh forty-eight thousand seven hundred twenty-six and seven lakh three thousand one hundred eighty-nine, respectively.
What is Face Value and Place Value?
- The face value of a digit is the actual value of the digit itself, irrespective of its position in a number.
- The place value of a digit in a given number is its value due to its place or position in the number.
- Consider the numbers 81,246 and 1,34,279.
- Here, the place values of 4 are 4 tens (= 40) and 4 thousands (4,000), respectively.
The face value of 4 is 4 in both the numbers.
 Difference between Face value and Place value
Difference between Face value and Place value
Edurev Tips:
- Place value = Face value × value of the place
- The place value and face value of 0 is always 0.
Example 1: Write the face value and place value of each digit in 1 72 827.
Sol:
How to Write in Expanded Notation?
The number 23,344 in the expanded notation is written as:
23,344 = 2 ten thousands + 3 thousands + 3 hundreds + 4 tens + 4 ones
= 20,000 + 3,000 + 300 + 40 + 4
Let us consider the number 4,78,362 in the expanded notation.
4,78,362 = 4 lakhs + 7 ten thousands + 8 thousands + 3 hundreds + 6 tens + 2 ones
= 4,00,000 + 70,000 + 8,000 + 300 + 60 + 2
Edurev Tips: In expanded notation, a number is written as the sum of the place values of its digits.
How to Compare and Ordering Numbers?
Case 1: Comparing Numbers with Different Number of Digits
Rule: A number containing greater number of digits is larger than a number containing lesser number of digits.
54,207 > 8,964
(5 digits) (4 digits)
Example 1: Which is the greatest: 3,815 or 567 or 36,812?
Sol:
If you write these numbers on the number line, the number 567 will come first, then 3,815 and then 36,812, from the left to right. Since 567 is to the left of 3,815, therefore, 567 < 3,815 or 3,815 > 567.Also, since 3,815 is to the left of 36,812, therefore, 3,815 < 36,812 or 36,812 > 3,815.Therefore, 36,812 is the greatest.
Case 2: Comparing Numbers with Same Numbers of Digits
Rule: To compare numbers with equal number of digits, start by comparing the digits from the leftmost place till you find two different digits. Compare these digits to decide the greater and smaller of the given numbers.
Example: Which is greater: 32,719 or 45,989?
Sol:
Both are 5-digit numbers but the number 32,719 has 3 ten thousands, while the number 45,989 has 4 ten thousands.
Since 4 ten thousands is greater than 3 ten thousands, therefore, 45,989 > 32,719.
Example: Which is greater: 7,32,612 or 7,32,545?
Sol:
Both the numbers are 6-digit numbers and both have 7 lakh 32 thousands. But the number 7,32,612 has 6 hundreds, while the number 7,32,545 has 5 hundreds.
Therefore, 7,32,612 > 7,32,545.
How to Write in Ascending and Descending Orders?
- Numbers, when arranged from the smallest to the greatest, are said to be in ascending order.
- Numbers, when arranged from the greatest to the smallest, are said to be in descending order.

Example: Arrange the following numbers in ascending order.
12,675 6,532 62,392 18,125 29,358
Sol:
The smallest number is 6,532. The next number greater than 6,532 is 12,675. The next number greater than 12,675 is 18,125. The other numbers greater than 18,125 in order are 29,358 and 62,392.
∴ 6,532 < 12,675 < 18,125 < 29,358 < 62,392.
Hence, the above numbers when arranged in ascending order are:
6,532 12,675 18,125 29,358 62,392.
What is Successor and Predecessor?
- The successor of a whole number is the number obtained by adding 1 to it. So, the successor of 0 is 1, the successor of 1 is 2, and so on.
- The predecessor of a whole number is one less than the given number. So, the predecessor of 1 is 0, the predecessor of 2 is 1, and so on.
Look at some examples of successor and predecessor of a number:
How to Form Numbers using the Given Digits?
1. Smallest Number
To write the smallest number using the given digits, arrange the digits in ascending order.
- If 0 is one of the digits, it takes the second place after the smallest digit.
- If two of the given digits are equal, then write them one after the other.
2. Greatest Number
To write the greatest number using the given digits, arrange the digits in descending order.
- If two of the given digits are equal, write them one after the other.
Edurev Tips: Zero occupies the second highest position in forming the smallest number.
Example: Use 6, 2, 1, 8 to build the greatest and the smallest 4-digit numbers.
Sol:
Greatest number: Arranging the digits in descending order, we get 8,621.
Smallest number: Arranging the digits in ascending order, we get 1,268.
Example: Use 1, 5, 0, 8, 3 to build the greatest and the smallest 5-digit numbers.
Sol:
Greatest number: 85,310, Smallest number: 10,358
How to Round off the Numbers?
In our daily life, we hear statements like the following:
- Sarita said that she weighs about 40 kg. She weighs 41 kg.
- Mr Dubey paid ₹ 675 for a coat. To his friend, he said, “The coat cost me nearly ₹ 700.”
- About 25,000 people watched the IPL match. 24,750 people watched the match.
In all the statements given above, the given number is being replaced by another number that is “close to” or is an approximation of it. This is called rounding off the given number to a chosen place value. In the first statement, the given number is rounded off to the nearest ten and in the second and third statements, the given number is rounded off to the nearest hundred.
1. Rounding off the Numbers to the Nearest Ten
To round off a number to the nearest ten, we round it off to the multiple of ten nearest to it.
In general, for rounding off a number to the nearest ten, look at the digit in the ones place. If it is 1, 2, 3 or 4, then round down the number to the lesser ten. If the digit is 5, 6, 7, 8 or 9, then round up the number to the greater ten.
Example:
- 57 is rounded off to 60. Ones digit is 7, so round up to the greater ten.
- 512 is rounded off to 510. Ones digit is 2, so round down to the lesser ten.
- 1,965 is rounded off to 1,970.
- 12,785 is rounded off to 12,790.
2. Rounding off the Numbers to the Nearest Hundred
To round off a number to the nearest hundred, we round it off to the multiple of hundred nearest to it.
In general, for rounding off a number to the nearest hundred, look at the digit at the tens place. If it is 1, 2, 3 or 4, round down to the lesser hundred. If the digit is 5, 6, 7, 8 or 9, round up to the greater hundred.
Examples:
- 729 is rounded off to 700. Tens digit is 2, so round down.
- 1,550 is rounded off to 1,600. Tens digit is 5, so round up.
- 24,874 is rounded off to 24,900. Tens digit is 7, so round up.
- 84,214 is rounded off to 84,200.
3. Rounding off the Numbers to the Nearest Thousand
To round off a number to the nearest thousand, we round it off to the multiple of thousand nearest to it.
In general, for rounding off a number to the nearest thousand, look at the digit at the hundreds place. If it is 1, 2, 3 or 4, round down to the lesser thousand. If the digit is 5, 6, 7, 8 or 9, round up to the greater thousand.
Example:
- 8,958 is rounded off to 9,000. Hundreds digit is 9, so round up.
- 16,349 is rounded off to 16,000. Hundreds digit is 3, so round down.
- 29,500 is rounded off to 30,000.
International Numeral System
In the international numeral system, the sequence of place values for digits progresses as follows: Ones, Tens, Hundreds, Thousands, Ten Thousands, Hundred Thousands, Millions, Ten Millions, and so forth.
In the number 12,345,678 the place values of each digit are:
- 8 – Ones
- 7 – Tens
- 6 – Hundreds
- 5 – Thousands
- 4 – Ten Thousand
- 3 – Hundred Thousands
- 2 – Millions
- 1 – Ten Million
The relations between them are:
- 1 hundred = 10 tens
- 1 thousand = 10 hundreds = 100 tens
- 1 million = 1000 thousand
- 1 billion = 1000 millions

Comparison Between Indian and International Numeral System
Comparing the two numeral systems we observe that:
- 100 thousand = 1 lakh
- 1 million = 10 lakhs
- 10 millions = 1 crore
- 100 millions= 10 crores

Comma Placement:
- Commas are used in large numbers to facilitate readability and writing. In both the Indian and international numeral systems, commas are positioned differently.
- In the Indian numeral system, the initial comma is inserted after the hundreds place, followed by additional commas every two digits. For example, 1,23,45,67,890.
- In the international numeral system, the initial comma is positioned after the hundreds place, and subsequent commas are added after every three digits. For instance, 1,234,567,890.
All about One Crore!
In order to understand what One Crore is, we need to understand what One Lakh is:
- One Lakh is the number 100000.
The number 100000 is one hundred thousand or 1 lakh.
It is a 6-digit number including 5 zeros.
Number 100000 is the smallest 6 digit number.
Have a look at the smallest 6,4,3,2 & 1 digit numbers below.

We learnt about One Lakh! Come on! Let’s learn about 100 Lakh or One Crore now!
- The number 10000000 is read as (100 lakh) or 1 crore.
- Yeaaaa! 100 Lakh is One Crore!
- Similarly, 50000000 is read as ‘five crores’.
- 80000000 is read as ‘eight crores’.
Wooohoooo! You and Ria have mastered the concepts of Crore now!
- One Crore is the number 10000000 or 100 Lakh and 1 lakh is the number 100000 or One Hundred Thousand.
Do you know?
The moon is approximately 384400 km away from the Earth. It is a huge number as well!
In the image Earth and Moon look very near but it in reality it isn't so.
Greatest Digit Numbers
- Have a look on Greatest 5 digit number.

Tell us!
Which is the greatest 8 digit number and how can we get the smallest 9 digit number from it?
- 99999999 is the greatest 8-digit number and is read as ‘nine crore ninety-nine lakh ninety-nine thousand nine hundred ninety-nine.
- If we add 1 to this number, we get the smallest 9-digit number.

- 100000000 is read as ‘ten crore’.
- Similarly, 200000000 is read as ‘twenty crore’.
- 400000000 is read as ‘forty crore’.
Tell us again!
Which is the greatest 8 digit number and how can we get the smallest 9 digit number from it?
- 999999999 is the greatest 9-digit number and is read as ‘ninety-nine crore ninety-nine lakh ninety-nine thousand nine hundred ninety-nine’.
- If you add 1 to this number, you will get the smallest 10-digit number. 1000000000 is read as ‘hundred crore’ or ‘one arab’.

What are Place Values?
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number.
- When we represent the number in general form, the position of each digit will be expanded.
- Those positions start from a unit place or we also call it one’s position.
- The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
- Let us understand with the help of an example, say 7231468, and see below figure for the place value of each digit.
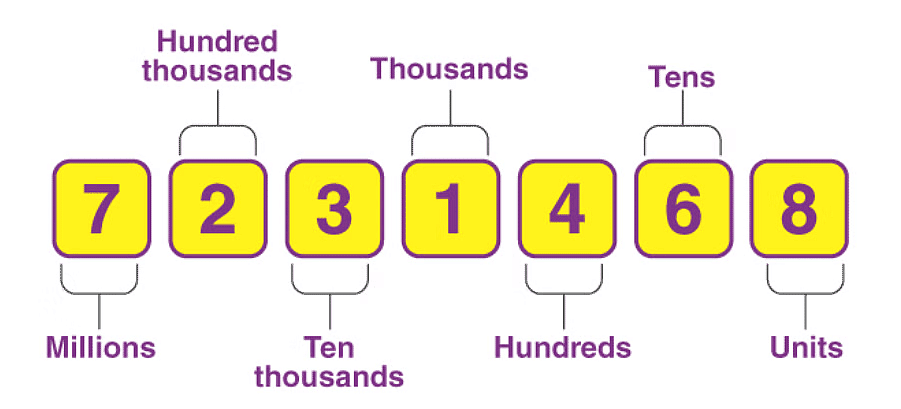 Place Value of number 7231468
Place Value of number 7231468
- Look at the place value chart below for the first nine digits in the Indian system of numeration.
 Place Value Chart Indian system of Numeration
Place Value Chart Indian system of Numeration
- The first period consisting of three digits is called units or ones period, the next period consisting of two digits is called thousands period.
- Next period also consisting of two digits is called lakhs period and the next period which also consists of two digits is called crores period.
How to Read Large Numbers?
- To read a large number, divide the number into periods starting from the right.
- For separating periods, we put a comma after three digits starting from the right and then we put a comma after every two digits.
- The modern convention is to leave space to separate different periods instead of putting a comma between them. Thus, the numbers 75,80,72,608 would be written as 75 80 72 608.

While reading a numeral, all the digits in the same period are read together and the name of the period (except the ones) is read together.
Thus, the above number is read as ‘seventy-five crore eighty lakh seventy-two thousand six hundred eight’.
Edurev Tips:
We should not write the word ‘and’ here as per the common practice.
We do not use the words indicating the periods in plural form. Thus, we write seventy-five crore and not seventy-five crores.
The population of Japan in the year 2018 was about 12,71,85,332.
- A place value chart can help to explain what the number means.

- The different ways in which 12,71,85,332 can be written are:

What are Roman Numerals?
- Romans developed a different system of numeration about 2000 years ago, known as Roman numerals.
- The ancient Romans explained that when a number reaches 10 it is not easy to count on one’s fingers. Therefore, there was a need to create a proper number system that could be used for trade and communications.
- Roman numerals are denoted using a different combination of symbols that include the English alphabet.
- There are seven basic Roman numerals.
- These numerals and their corresponding Hindu-Arabic numerals are given below.
 Seven Basic Roman Numerals
Seven Basic Roman Numerals
How to Write Hindu Arabic Numbers in Roman Numerals?
We can convert any Roman Numeral into a Hindu-Arabic number, also Hindu-Arabic number can be written in the form of a Roman Numeral.
 Roman Numerals Chart
Roman Numerals Chart
Note: In the Roman number system there is no symbol for zero.
Roman Letters
- The Roman letters are English alphabets but keep in mind that not all of the alphabets are Roman alphabets.
- There are 23 Roman alphabets out of 26 English alphabets, in which J, U, and W are not considered Roman alphabets. Hence, the Roman alphabets are:
- A, B, C, D, E, F, G, H, I, K, L, M, N, O, P, Q, R, S, T, V, X, Y, and Z. These Roman letters are also called Roman symbols.
- For example, the year 2022 is written as MMXXII.
Large Roman Numerals
With the help of the chart given below, you can write large numbers in Roman numerals.
 Large numbers in Roman numerals
Large numbers in Roman numerals Chart of Roman Numerals from 1 to 10,000
 Charts of Roman Numerals from 1 to 10,000
Charts of Roman Numerals from 1 to 10,000
Roman Number 1 to 100
Following is the list of Roman numerals from 1 to 100.

Steps to write Roman Numerals
Rule Number 1
When a letter is used more than once, we add its value each time to get the number.
Examples:
II = 1 + 1 = 2
XXX = 10 + 10 + 10 = 30
CCC = 100 + 100 + 100 = 300
MM = 1000 + 1000 = 2000
MMM = 1000 + 1000 + 1000 = 3000
Tips:
- The same symbol cannot be repeated more than 3 times together.
- The symbols V, L, and D are never repeated.
 Check out the correct way of writing 45 in Roman Numerals!
Check out the correct way of writing 45 in Roman Numerals!
Rule Number 2
When a symbol of a smaller value is written to the right of a symbol of a larger value, add the two values.
Examples:
VII = 5 + 1 + 1 = 7
XII = 10 + 1 + 1 = 12
XXVII = 10 + 10 + 5 + 1 + 1 = 27
LVII = 50 + 5 + 1 + 1= 57
LXVI = 50 + 10 + 5 + 1 = 66
CVII = 100 + 5 + 1 + 1 = 107
CLXV = 100 + 50 + 10 + 5 = 165
DC = 500 + 100 = 600
MDCXVIII = 1000 + 500 + 100 + 10 + 5 + 1 + 1 + 1 = 1618
 Roman Numerals
Roman Numerals
Rule Number 3
When a symbol of a smaller value is written to the left of a symbol of a larger value, the smaller value is subtracted from the larger value.
Examples:
IV = 5 – 1 = 4
IX = 10 – 1 = 9
XL = 50 – 10 = 40
XC = 100 – 10 = 90
CD = 500 – 100 = 400
CM = 1000 – 100 = 900
Tips:
- V, L, and D are never subtracted.
- I can be subtracted from V and X only once.
- X can be subtracted from L and C only once.
- C can be subtracted from D and M only once.
- Thus, I or V is never written to the left of L or C. L is never written to the left of C.
Example 1: Write the following in Roman numerals.
(a) 45
45 = 40 + 5 = XL + V = XLV
(b) 99
99 = 90 + 9 = XC + IX = XCIX
(c) 92
92 = 90 + 2 = XC + II = XCII
(d) 78
78 = 50 + 20 + 5 + 3 = L + XX + V + III = LXXVIII
(e) 181
181 = 100 + 80 + 1 = C + LXXX + I = CLXXXI
Example 2: Write the following in Hindu-Arabic numerals.
(a) LXV
LXV = L + X + V = 50 + 10 + 5 = 65
(b) LIII
LIII = L + III = 50 + 3 = 53
(c) CDXCIX
CDXCIX = CD + XC + IX = 400 + 90 + 9 = 499
Rule Number 4
A symbol cannot be repeated more than three times. Example:
Rule Number 5
1000 can be represented by a line on the letter, which is called a bar.
Example:

Question for Notes: NumbersTry yourself: Which Roman numeral represents the number 50?
View Solution
Rule Number 6
Also, the letter used in mixed form can be determined as an integer.
Example:

Roman Numerals to Hindu Arabic Numbers
Rule for addition:
Step 1: First we convert the given Roman numerals into Hindu-Arabic numbers.
Step 2: Then we add the Hindu-Arabic numbers.
Step 3: Now again we convert the Hindu-Arabic number (number from Step 2) into Roman Numerals.
Example: Add LV and XV.
Solution:
Here,
(i) LV = L +V = 50 + 5 = 55
(ii) XV = X + V = 10 + 5 = 15
Now, LV + XV will be 55 + 15 = 70
Now, 70 = 50 + 10 + 10 = L + X + X = LXX
Finally, we get, LV + XV = LXX.
Rule for subtraction:
Step 1: First we convert the given Roman numerals into Hindu-Arabic numbers.
Step 2: Then we subtract the Hindu-Arabic numbers.
Step 3: Now again we convert the Hindu-Arabic number (number from Step 2) into Roman Numerals.
Example: Subtract XXVII from LXXXVIII.
Solution:
Here, XXVII = X + X + V + I + I = 10 + 10 + 5 + 1 + 1 = 27
LXXXVIII = L + X + X + X + V + I + I + I = 50 + 10 + 10 + 10 + 5 + 1 + 1+ 1 = 88
Now, LXXXVIII – XXVII will be 88 – 27 = 61
61 = 50 + 10 + 1
= L + X + I = LXI
|
41 videos|151 docs|72 tests
|
FAQs on Notes: Numbers - Mathematics & Pedagogy Paper 1 for CTET & TET Exams - CTET & State TET
| 1. What are the key differences between place value and face value of a number? |  |
| 2. How do you write the expanded form of a number? |  |
| 3. How can I identify even and odd numbers? |  |
| 4. What is the method to read and write 5-digit and 6-digit numbers? |  |
| 5. What is numeration, and why is it important in mathematics? |  |
|
41 videos|151 docs|72 tests
|

|
Explore Courses for CTET & State TET exam
|

|


 We have, 36,207 = Thirty-six thousand two hundred seven.Similarly, 50,327 = Fifty thousand three hundred twenty-seven.
We have, 36,207 = Thirty-six thousand two hundred seven.Similarly, 50,327 = Fifty thousand three hundred twenty-seven.
 We represent the smallest 6-digit number 1,00,000, in the Indian place value chart, as shown below:
We represent the smallest 6-digit number 1,00,000, in the Indian place value chart, as shown below: 1 is in the lakhs place. So, 1,00,000 is read as 1 lakh.
1 is in the lakhs place. So, 1,00,000 is read as 1 lakh.

 If you write these numbers on the number line, the number 567 will come first, then 3,815 and then 36,812, from the left to right. Since 567 is to the left of 3,815, therefore, 567 < 3,815 or 3,815 > 567.Also, since 3,815 is to the left of 36,812, therefore, 3,815 < 36,812 or 36,812 > 3,815.Therefore, 36,812 is the greatest.
If you write these numbers on the number line, the number 567 will come first, then 3,815 and then 36,812, from the left to right. Since 567 is to the left of 3,815, therefore, 567 < 3,815 or 3,815 > 567.Also, since 3,815 is to the left of 36,812, therefore, 3,815 < 36,812 or 36,812 > 3,815.Therefore, 36,812 is the greatest. Since 4 ten thousands is greater than 3 ten thousands, therefore, 45,989 > 32,719.
Since 4 ten thousands is greater than 3 ten thousands, therefore, 45,989 > 32,719. Therefore, 7,32,612 > 7,32,545.
Therefore, 7,32,612 > 7,32,545.





















