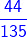Olympiad Notes: Fractions | Maths Olympiad Class 6 PDF Download
Introduction
- A fraction represents a portion of a whole entity.
- The "whole" can be either an individual object or a collection of objects.
- Each part of the whole must be of equal size in order for the fraction to be accurate.
- Fractions enable the representation of parts or segments in relation to the whole.
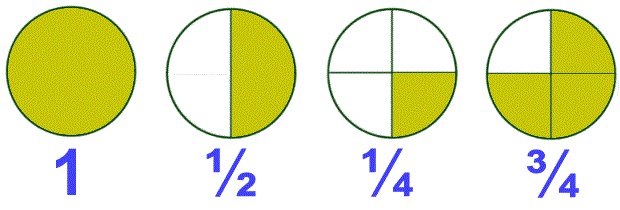
The first one is the whole i.e. a complete circle.
In the second circle, if we divide the circle into two equal parts then the shaded portion is the half i.e. ½ of the circle.
In the third circle, if we divide the circle into four equal parts and shade only one part then the shaded part is the one fourth i.e. ¼ of the whole circle.
In the fourth circle, if we divide the circle into four equal parts and shade three parts then the shaded part is the three fourth i.e. ¾ of the whole circle.
Numerator and Denominator
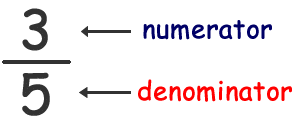
- The upper part of the fraction is called Numerator. It tells the number of parts we have.
- The lower part of the fraction is called Denominator. It tells the total parts in a whole.
- For example, the given example reads as "three-fifths".
Representation of fraction on Number line
Example:
Sol:
- Draw a number line.
- We know that ½ is less than 1 and greater than 0, so we have to divide the gap between two equal parts and then mark the middle point as ½.
- As the denominator is the whole and the numerator is the part, so we have to divide the gap between 0 and 1 in the number of parts as the denominator is given.
Example: For 1/3, divide into 3 equal parts.
For ¼, divide into 4 equal parts and so on.
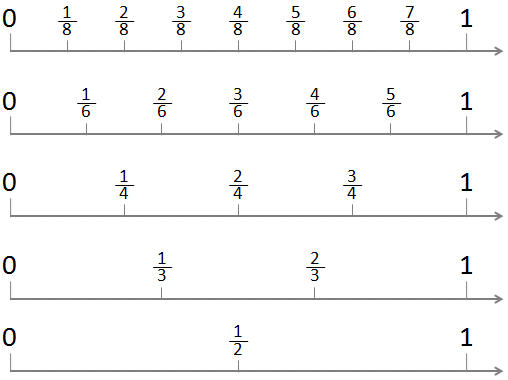
Proper Fractions
- A fraction with a smaller numerator than denominator is termed a proper fraction.
- When graphed on a number line, a proper fraction consistently falls between 0 and 1.
- Proper fractions denote values less than the whole unit.
Examples: 
Improper fractions and Mixed fractions
Improper Fraction
When the numerator is greater than the denominator then it is called Improper fraction.
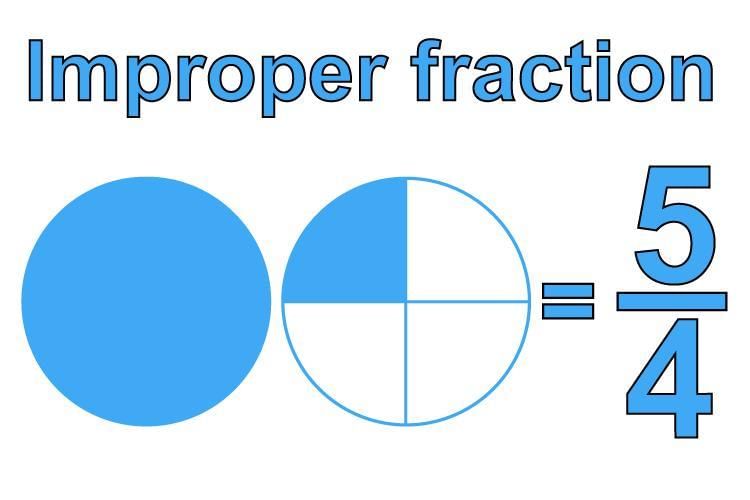
The above fraction is made by adding one whole part and one-fourth part.
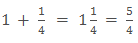
Mixed Fractions
- A combination of a whole and a part is said to be a mixed fraction.
- Examples of Mixed Fractions:
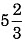 ,
,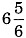
Conversion of improper fraction into mixed fraction
- Converting an improper fraction into a mixed fraction involves dividing the numerator by the denominator.
- The quotient becomes the whole number part of the mixed fraction.
- The remainder, if any, becomes the numerator of the fractional part.
- The denominator remains the same as in the original improper fraction.
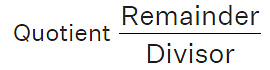
Example: Improper fraction to Mixed Fraction
Improper fraction to Mixed Fraction
Convert Mixed fraction into Improper fraction
A mixed fraction is in the form of 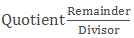
We can convert it in the form of an improper fraction by
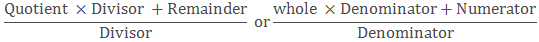
Example: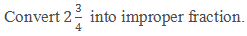
Sol: 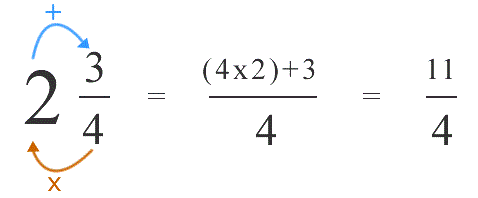
Equivalent Fractions
Equivalent fractions are those fractions which represent the same part of a whole.
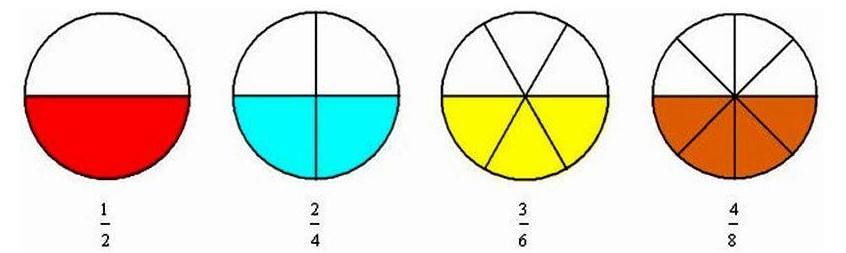
All the above images are different but equivalent fractions as they represent the same i.e. half part of a whole circle.
- The general form for Equivalent fraction can be written as:
If is any fraction and
is any fraction and  be its equivalent fraction then,
be its equivalent fraction then, =
=  such that ps = rq where p, q, r, and s are whole numbers such that q and s are non-zero non zero whole numbers.
such that ps = rq where p, q, r, and s are whole numbers such that q and s are non-zero non zero whole numbers.
Finding equivalent fractions
1. Multiplying the same number
If we multiply the numerator and denominator of any fraction with the same number then we will get the equivalent fraction. There could be more than one equivalent fractions of one fraction.
Example: Find three equivalent fraction of ½.
Sol: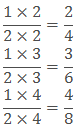
2. Dividing the Same number
If we divide the numerator and denominator of any fraction with the same number then we will get the equivalent fraction.
Example: Find the equivalent fraction of 18/27 with denominator 9.
Sol: To get the denominator 9 we need to divide it by 3.
So, to find the equivalent fraction we need to divide the fraction by 3.
Hence, the equivalent fraction with denominator 9 is 6/9.
The Simplest Form of a Fraction
If the numerator and denominator do not have any other common factor than 1, then it is said to be the simplest or lowest form of that fraction.Example:
To find the equivalent fraction which is the simplest form we have to find the HCF of numerator and denominator and then divide them both by that HCF.
Example: Reduce the fraction 18/27 in the simplest form.
Sol: HCF of 18 and 27 is 9.
Hence,
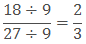
2/3 is the lowest form of 18/27.
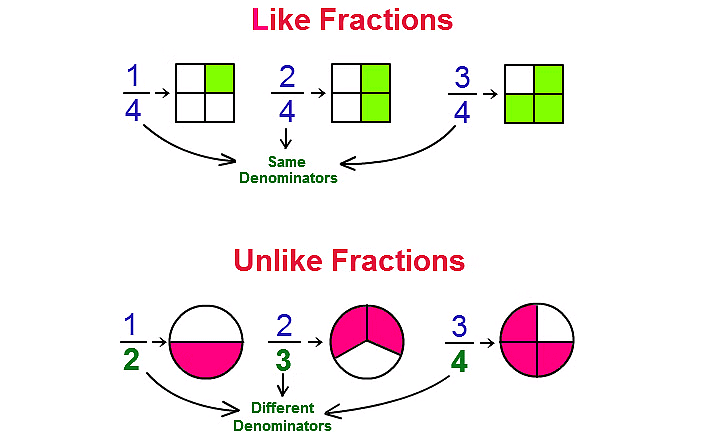
Like Fractions and Unlike Fractions
Like Fractions
- Fractions which have same denominators are known as Like fractions.
- Example:
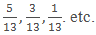
Unlike Fractions
- Fractions which have different denominators are known as unlike fractions.
- Example:
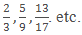
Comparing fractions
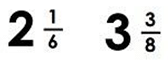
If we have to compare the above two fractions then it is easy as the first one is less than 3 and the second one is greater than 3. So we can clearly say that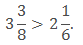
But sometimes it is not easy to compare it so easily. So we need some accurate procedure.
Comparing Like fractions
- Like fractions are the fractions with the same denominator.
- Comparing these fractions involves determining which has the greater numerator.
- The fraction with the larger numerator is greater in value.
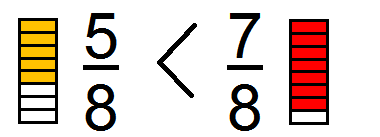
- In the above example, both are divided into 8 equal parts, so the fraction with seven shaded part is greater than the 5 shaded parts.
Comparing Unlike fractions
The fractions with different denominators are unlike fractions.
1. Unlike fraction with the Same Numerator
- If we have to compare the fractions with different denominator but same numerator, we have to compare with the denominator only.
- In that case, the fraction with the small denominator is greater than the other.
Example:
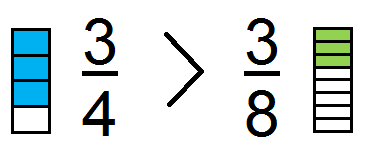
Here the numerator is same i.e.3 so we will compare with the denominator.
The fraction with small denominator i.e. ¾ is greater than the fraction with the large denominator i.e. 3/8.
Unlike fraction with Different Numerators
- If the numerator and denominator both are different, then we have to make the denominator same by finding the equivalent fraction of both the fractions.
- After finding equivalent fraction, compare the fractions as like fractions.
- To find the equivalent fraction of both the fractions with the same denominator, we have to take the LCM of the denominator.
Example: Compare 6/7 and 3/5.
Sol: The product of 7 and 5 is 35.
So we will find the equivalent fraction of both the fractions with the denominator 35.
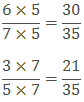
Now we can compare them as like fractions.
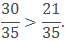
Addition and Subtraction of Fractions
Addition and subtraction of fractions involve combining or taking away portions of quantities represented by the fractions.Adding and Subtraction of Like Fractions
When we add or subtract like fractions, we add or subtract their numerators and the denominator remains the same.1. Steps to Add like fractions
- Add the numerators.
- Leave the common denominator same. (Don’t add the denominator).
- Write the answer as
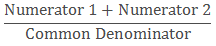
Example: 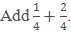
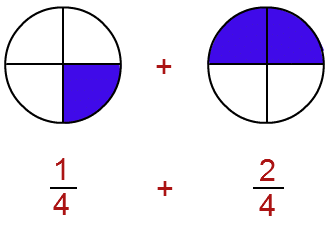
Sol:
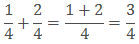
2. Steps to Subtract Like fractions
- Subtract the small numerator from the bigger one.
- Leave the common denominator same.
- Write the answer as

Example: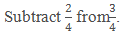
Sol: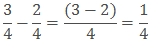

Addition and Subtraction of two Unlike Fractions
When we add or subtract unlike fractions we follow the following steps:
1)  +
+ 
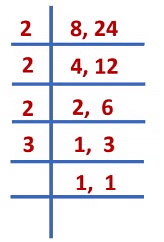
The given fractions are unlike fractions, so we first find LCM of their denominators.LCM of 8 and 24 = 2 × 2 × 2 × 3 = 24
Now, we convert the fractions into like fractions.
(Changing the denominator of fractions to 24)
=
and
+
= =
2)  −
− 
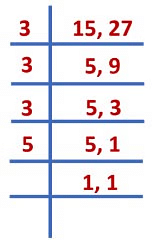
As the given fractions are unlike fractions, we find the LCM of their denominator.LCM of 15 and 27 = 3 × 3 × 3 × 5 = 135
Next, we convert the fractions into like fractions
(Fractions with the same denominator)
=
and
=
-
=
=
Addition and Subtraction of Mixed Fractions
Note: Before applying any operations such as addition, subtraction, multiplication, etc., change the given mixed fractions to improper fractions.
After converting the mixed fractions to improper fractions, one can proceed with the calculations, which are as follows:
Adding Mixed Fractions
When it comes to adding Mixed or Improper fractions, we can have either the same denominators for both the fractions to be added or the denominators can differ too.
Adding the Improper fraction with Same or Different denominators.
 Adding improper fraction with same or different denominators
Adding improper fraction with same or different denominators
Subtracting Mixed Fractions
Subtracting the improper fraction with Same or Different Denominators.

|
31 videos|122 docs|60 tests
|
FAQs on Olympiad Notes: Fractions - Maths Olympiad Class 6
| 1. How do you represent fractions on a number line? |  |
| 2. What is the difference between proper fractions, improper fractions, and mixed fractions? |  |
| 3. How do you find equivalent fractions? |  |
| 4. How can you simplify a fraction to its simplest form? |  |
| 5. How do you compare fractions with different denominators? |  |