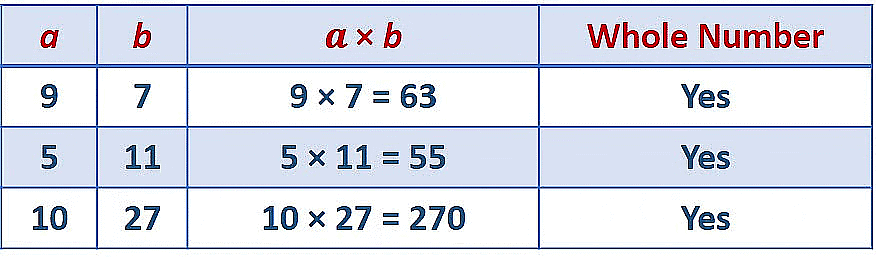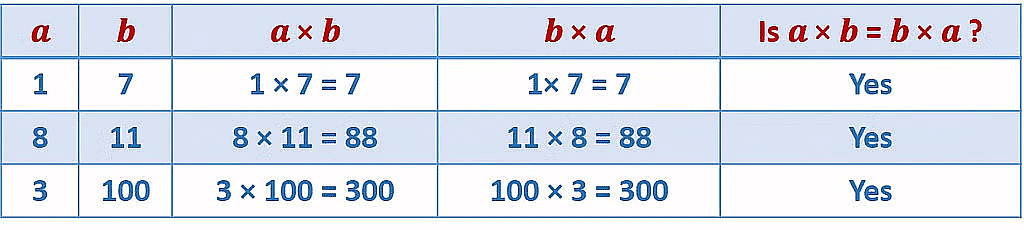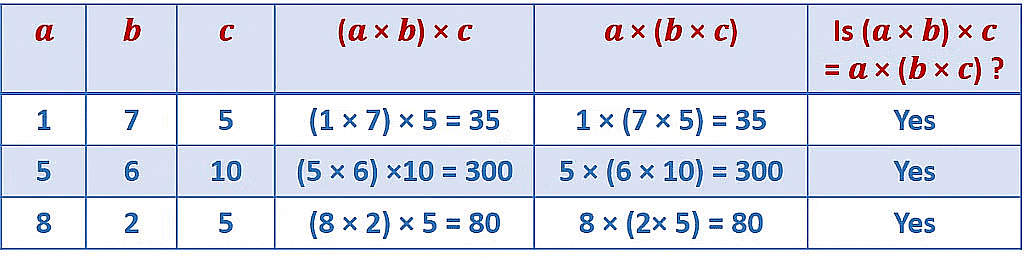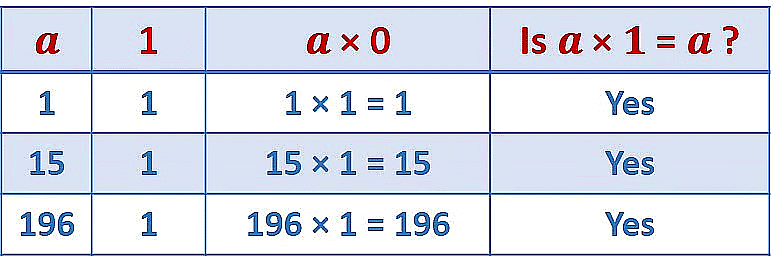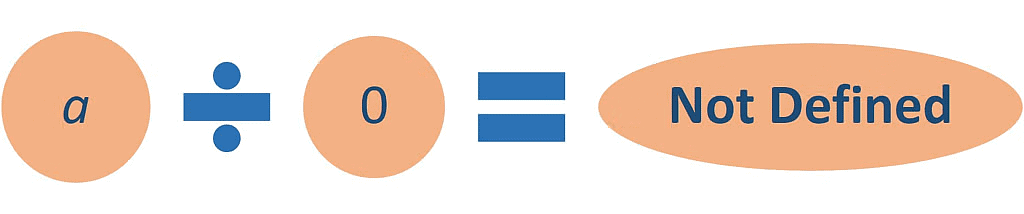Olympiad Notes: Whole Numbers | Maths Olympiad Class 6 PDF Download
| Table of contents |

|
| Introduction |

|
| Whole numbers on a number line |

|
| Operations on a number line |

|
| Predecessor and Successor |

|
| Properties of subtraction |

|
Introduction
- Numbers play an important role in our life.
- We use numbers in our day to day life to count things.
- While counting we use numbers to represent any quantity, to measure any distance or length.
3 apples and 3 pepper Discount City distance Length of the table
- The counting numbers starting from 1, 2, 3, 4, 5, ……… are termed as natural numbers.
- The set of counting numbers and zero are known as whole numbers.
- Whole numbers are 0, 1, 2, 3, 4, 5, 6, 7,…….. and so on.

Example: Write the next three natural numbers after 10999.
Solution: 10999 + 1 = 11000
11000 + 1= 11001
11001 + 2 = 11002.
Thus, 11000, 11001, 11002 are the next three natural numbers after 10999.
Whole numbers on a number line
Number Line
A pictorial representations of numbers evenly marked on a straight line is known as a number line.
- To mark whole numbers on a number line draw a horizontal line and mark a point on it as 0.
- Extend this line towards right direction.
- Starting from 0, mark points 1, 2, 3, 4, 5, 6, 7, 8, 9….on a line at equal distance towards right side.

- There is no whole number on the left of zero. Therefore zero is the smallest whole number.
Comparison using Number Line
The number line also helps us to compare two whole numbers. i.e., to decide which of the two given whole numbers is greater or smaller.
- A whole number is greater than all the whole numbers which lie to the left of it on the number line.
- A whole number is less than all the whole numbers which lie to the right of it on the number line
Example: We can say that 5 is less than 9 and write 5 < 9.
We can also say that 5 is greater than 4 and write 5 > 4.
Example: Identify which whole number comes first on the number line in each pair and write the appropriate sign (> or <) between them:
(a) 507 and 503
(b) 338 and 342
Sol: (a) 503 is on the left side of 507 on the number line. So, 507 > 503.
 (b) 338 is on the left side of 342 on the number line. So, 342 > 338.
(b) 338 is on the left side of 342 on the number line. So, 342 > 338.
Operations on a number line
Addition
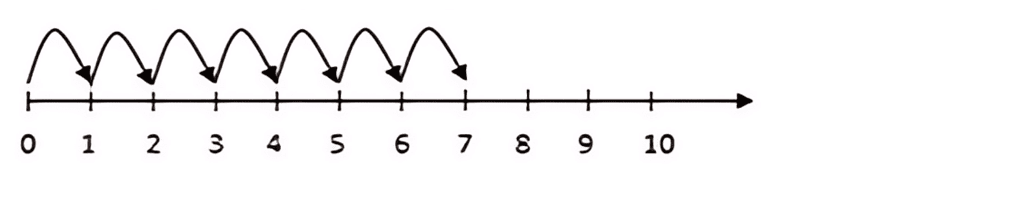
For eg: Add 2 and 5. i.e 2 + 5.
- Start from 0, 2 jumps towards right. You reach at 2.
- Start from 2, 5 jumps towards right. You reach at 7.
- Therefore, 2 + 5 = 7.

Subtraction
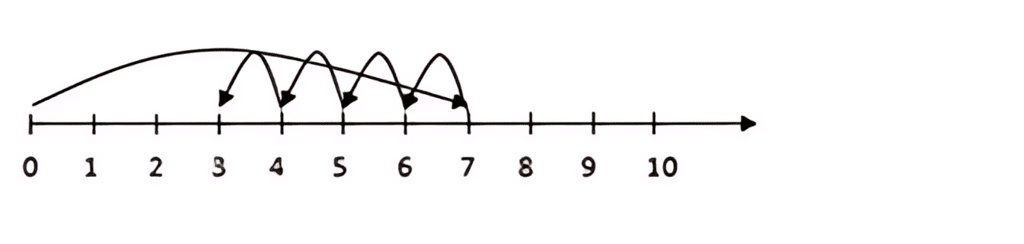
For eg: Subtract 4 from 7. i.e 7 - 4.
- Start from 0, jump directly to 7.
- Start from 7, 4 jumps towards left. You reach at 3.

Multiplication
For eg: Multiply 3 and 2 i.e. 3 x 2
- Multiplication means repeated addition. Thereofore 3 x 2 means 3 added twice.
- Start from 0. Make 2 jumps (each jump of 3 units).You reach at 6.

Division
For eg: 6 ÷ 3 = 2.
- Start from 6 and subtract 3 for a number of times till 0 is reached.
- The number of times 3 is subtracted gives the quotient.

Ques: Using the number line, determine the following products:
(a) 3 x 3
(b) 4 x 2
Sol: (a)
- Start from 0. Make 1 jump of 3 steps towards right. You reach at 3.
- Start from 3. Make 1 jump of 3 steps towards right. You reach at 6.
- Start from 6. Make 1 jump of 3 steps towards right. You reach at 9.

Therefore, 3 x 3 = 9
(b)
- Start from 0. Make 1 jump of 4 steps towards right. You reach at 4.
- Start from 4. Make 1 jump of 4 steps towards right. You reach at 8.

Therefore, 4 x 2 = 8.
Predecessor and Successor
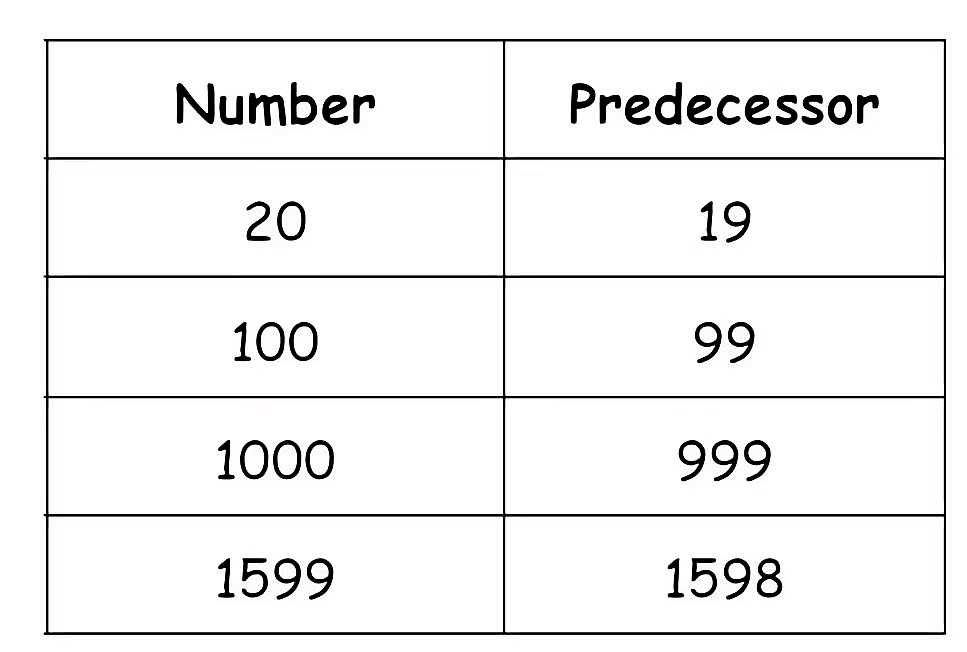
Predecessor
- The number which comes right before a given number is called its predecessor.
- The predecessor of a whole number found by subtracting 1 from it.
Number - 1 = Predecessor
Successor
- The number which comes right after a given number is called its successor.
- The successor of a whole number found by adding 1 to it.
Number + 1 = Successor.

Properties of addition
Closure property
- For any two whole numbers a and b, their sum a + b is always a whole number.
- For eg: 12 + 45 = 57. Here, 12, 45 and 57 all are whole numbers.

Commutative property
- For any two whole numbers a and b, a +b = b + a.
- We can add any two whole numbers in any order.
For eg: 12 + 45 = 45 + 12
Associative property
- For any three whole numbers a, b and c, (a + b) + c = a + (b + c).
- This means the sum is regardless of how grouping is done.
For eg: 31 + (24 + 38) = (31 + 24) + 38
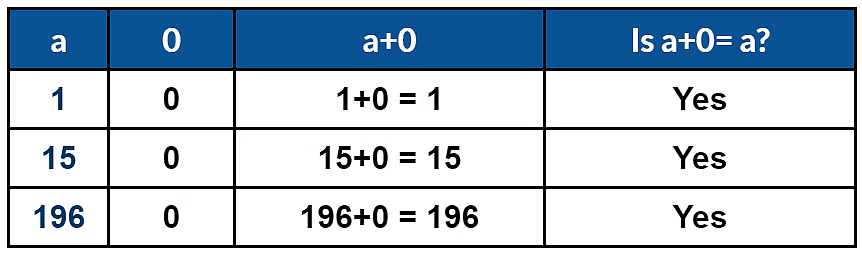
Additive identity property
- For every whole number a, a + 0 = a.
- Therefore ‘0’ is called the Additive identity.
E.g. 19 + 0 = 19
Example: Find the sum of 435, 216 and 165
Sol: 435 + 216 + 165
Now, 5 + 5 = 10. So, we add 435 + 165 first.
= (435 + 165) + 216
= 600 + 216 = 816
Example: Find the sum by suitable arrangement:
(a) 837 + 208 + 363
(b) 1962 + 453 + 1538 + 647
Sol: (a) 837 + 208 + 363
Now, 7 + 3 = 10.
So, we add 837 + 363 first.
= (837 + 363) + 208
= 1200 + 208 = 1408
(b) 1962 + 453 + 1538 + 647
Now, 2 + 8 = 10 .So, we make one group of (1962 + 1538)
3 + 7 = 10. Next we make another group of (453 + 647)
= (1962 + 1538) + (453 + 647)
=3500 + 1100 = 4600
Properties of subtraction
Closure property
- For any two whole numbers, a and b, if a > b then a – b is a whole number.
- If a < b then a – b is never a whole number.
- Closure property is not always applicable to subtraction.
E.g. 150 – 100 = 50, is a whole number but 100 – 150 = -50 is not a whole number.
Commutative property
- For any two whole numbers a and b, a – b ≠ b – a .
- Hence subtraction of whole number is not commutative.
E.g 16 – 7 = 9 but 7 – 16 ≠ 9
Associative property
- For any three whole numbers a, b and c, (a – b) – c ≠ a – (b – c).
- Hence subtraction of whole numbers is not associative.
E.g. 25 – (10 – 4) = 25 – 6 = 19
Also, (25 – 10) – 4 = 15 – 4 = 11. This means that 25 – (10 – 4) ≠ (25 – 10) – 4
(iv) If 𝒂 is any whole number other than zero, then 𝒂 – 𝟎 = 𝒂 but 𝟎 − 𝒂 is not defined.
For eg:
(i) 18 – 5 = 13 but 5 – 18 is not defined in whole numbers.
(ii) 30 – 12 = 18 but 12 – 30 is not defined in whole numbers
(v) If 𝒂, 𝒃 and 𝒄 are whole numbers such that 𝒂 – 𝒃 = 𝒄, then 𝒃 + 𝒄 = 𝒂
For eg:
(i) If 25 – 16 = 9 then 25 = 9 + 16,
(ii) If 46 – 8 = 38 then 46 = 38 + 8
Example: Solve the following:
(i) 367 – 99
= 367 + (– 100 + 1)
= 367 – 100 + 1
= (367 + 1) – 100
= 368 – 100
= 268
(ii) 5689 – 99
= 5689 + (- 100 +1)
= 5689 – 100 + 1
= (5689 + 1) – 100
= 5690 – 100
= 5590
Properties of multiplication
Closure property
- For any two whole numbers a and b,their product a x b is always a whole number.
- E.g. 12 x 7 = 84. Here, 12, 7 and 84 all are whole numbers.

Commutative property
- For any two whole numbers a and b, a x b = b x a.
- Order of multiplication is not important.
E.g 11 x 6 = 66 and 6 x 11 = 66 Therefore, 11 x 6 = 6 x 11.
Associative property
- For any three whole numbers a, b and c, (a x b) x c = a x (b x c).
- This means the product is regardless of how grouping is done.
E.g 8 x (4 x 5) = 8 x 20 = 160; (8 x 4) x 5 = 32 x 5 = 160 Therefore, 8 x (4 x 5) = (8 x 4) x 5
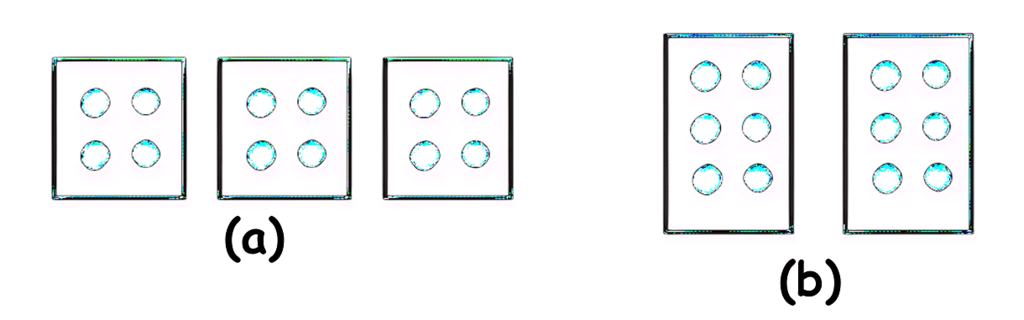
- We can explain the associative property with the help of following example
- Count the number of dots in figure (a) and figure (b)

- In figure (a), there are 2 rows and 2 columns which means 2 x 2 dots in each box. So the total number of dots are (2 x 2) x 3 = 12
- In figure (b), there are 3 rows and 2 columns which means 3 x 2 dots in each box. So the total number of dots are 2 x (3 x 2) = 12
- This explain the associative property of multiplication.
Multiplicative identity
- For any whole number a, a x 1 = a.
- Since any number multiplied by 1 doesn’t change its identity
- Hence 1 is called as multiplicative identity of a whole number.
E.g. 21 x 1 = 21
Multiplication by zero
- For any whole number a, a x 0 = 0,
- E.g 25 x 0 = 0

Distributive property of multiplication over Addition
- This property is used when we have to multiply a number by the sum.
- If 𝒂, 𝒃&𝒄 are any three whole numbers, then 𝒂 × (𝒃 + 𝒄) = 𝒂 × 𝒃 + 𝒂 × 𝒄.
Example: Find the product by suitable rearrangement:
(i) 4 × 1768 × 25
(ii) 2 × 166 × 50
(iii) 285 × 4 × 75
(iv) 625 × 279 × 16
Sol:
(i) 4 × 1768 × 25= (4 × 25) × 1768 (by commutative property)
= 100 × 1768 = 176800
(ii) 2 × 166 × 50= (2 × 50) × 166 (by commutative property)
= 100 × 166 = 16600
(iii) 285 × 4 × 75= 285 × (4 × 75) (by commutative property)
= 285 × 300 = 85500
(iv) 625 × 279 × 16= (625 × 16) × 279 (by commutative property)
= 10000 × 279 = 2790000
Properties of division
Closure property
- For any two whole numbers a and b, a ÷ b is not always a whole number.
- Hence closure property is not applicable to division.
For eg: 68 and 5 are whole numbers but 68 ÷ 5 is not a whole number.
Commutative property
- For any two whole numbers a and b, a ÷ b ≠ b ÷ a.
- This means division of whole number is not commutative.
For eg: 16 ÷ 4 ≠ 4 ÷ 16
Associative property
- For any 3 whole numbers a, b and c,(a ÷ b) ÷ c ≠ a ÷ (b ÷ c)
- For eg: consider (80 ÷ 10) ÷ 2 = 8 ÷ 2 = 4 80 ÷ (10 ÷2) = 80 ÷ 5 = 16 (80 ÷ 10) ÷ 2 ≠80 ÷ (10 ÷2)
- Hence division does not follow associative property.

Division by 1
- For any whole number a, a ÷ 1 = a.
- This means any whole number divided by 1 gives the quotient as the number itself.
For eg: 14 ÷ 1 = 14;
26 ÷ 1 = 26
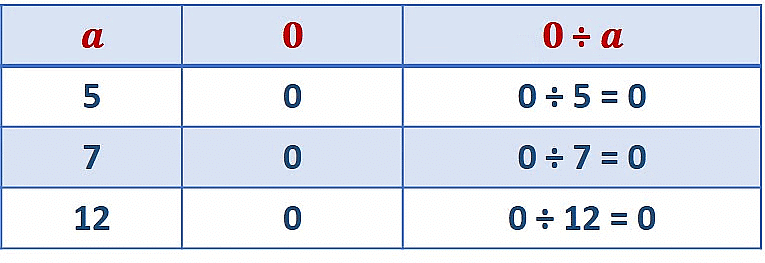
Division of 0 by any whole number
- For any whole number, a ≠ 0, 0 ÷ a = 0,
- This shows zero divided by any whole number (other than zero) gives the quotient as zero.
For eg: (i) 0 ÷ 1 = 0;
(ii) 0 ÷ 25 = 0;
Division by 0
- To divide any number, say 7 by 0, we first have to find out a whole number which when multiplied by 0 gives us 7. This is not possible.
- Therefore, division by 0 is not defined.

Example: Solve the following
(i) 636 ÷ 1
(ii) 0 ÷ 253
(iii) 246 – (121 ÷ 121)
(iv) (45÷ 5) – (9÷ 3)
Sol: (i) 636 ÷ 1 = 636 (∵ a ÷1 = a )
(ii) 0 ÷ 253 = 0 (∵ 0 ÷ a = 0)
(iii) 246 – (121 ÷ 121)
= 246 – (1)
= 246 – 1
= 245
(iv) (45÷ 5) – (9 ÷ 3)
= 9 – 3 = 6
|
8 videos|98 docs|60 tests
|
FAQs on Olympiad Notes: Whole Numbers - Maths Olympiad Class 6
| 1. What are whole numbers and how are they represented on a number line? |  |
| 2. What are the basic operations that can be performed on a number line using whole numbers? |  |
| 3. How do you find the predecessor and successor of a whole number on a number line? |  |
| 4. What are the properties of subtraction when working with whole numbers on a number line? |  |
| 5. How can whole numbers be applied in Olympiad exams and what are some key concepts to remember? |  |

|
Explore Courses for Class 6 exam
|

|