Overview: Circle | Quantitative Aptitude for SSC CGL PDF Download
| Table of contents |

|
| Sector |

|
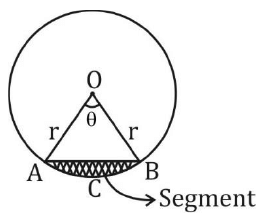
| Segment |

|
| Important Properties Of Circle |

|
| Solved Examples |

|
Sector
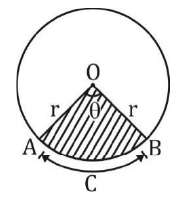

Segment
→ Area of segment = area of sector OACB – area of ∆OAB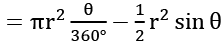
→ Perimeter = length of arc ACB + Chord length AB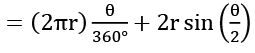
Q1. Find the area of a segment of a circle with a central angle of 120 degrees and a radius of 8 cm.
Sol. Area of segment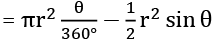
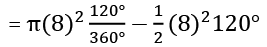
= 83.047
Q2. Find the area of a sector with an arc length of 30 cm and a radius of 10 cm.
Sol. Length of arc = 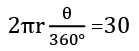
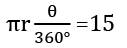
Area of sector OAB =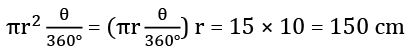
Q3. In a circle of radius 21 cm and arc subtends an angle of 72 at centre. The length of arc is?
Sol. Length of arc = 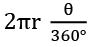
Important Properties Of Circle
Perpendicular from the centre of a circle to a chord bisects the chord.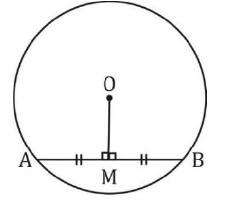
AM = MB
Q1. AB = 8 cm and CD = 6 cm are two parallel chords on the same side of the center of the circle.The distance between them is 1 cm. Find the length of the radius?
Sol.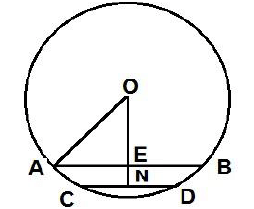 Let ON = x , AO = r
Let ON = x , AO = r
In triangle AOE
r2 = 16 + (x-1)2
In triangle OCN
r2 = 9 +x2
16 + (x-1)2 = 9 +x2
x=4
r2 = 9 +16, r = 5 cm
Chords corresponding to equal arcs are equal. If
If 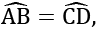 then chord , AB = CD
then chord , AB = CD
Equal Chords of Circle Subtends equal angles at the centre.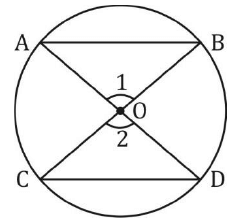 If AB = CD
If AB = CD
then ∠1 = ∠2
Equal chords of a circle are equidistance from the centre.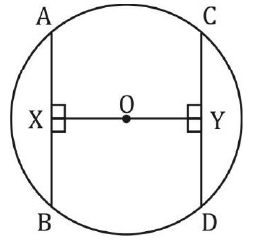
If AB = CD, Then OX = OY
The angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle. x = 2y
x = 2y
Q1. The length of chord of a circle is equal to the radius of the circle .The angle which this chord subtends in the major segment of the circle is equal to?
Sol. 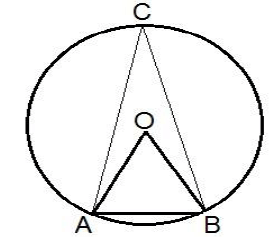 OA = OB = r
OA = OB = r
AB is equal to radius
Therefore triangle OAB is an equilateral triangle
Angle OAB = 60°
Angle ACB, angle which chord subtends at major angle = 
Angle in same segment of a circle are equal.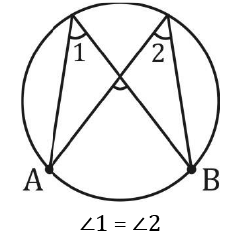 Angle in a semicircle is always a right angle.
Angle in a semicircle is always a right angle.

Q1. AC is the diameter of a circumcircle of triangle ABC. Chord ED is parallel to the diameter AC. If Angle CBE = 50°, then the measure of angle DEC is?
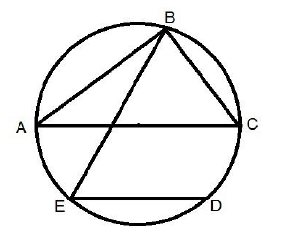
Angle CBE = 50°
Angle ABC = 90° (Angle in a semicircle is always a right angle)
Angle ABE = 90° - 50° = 40°
Angle ABE = Angle ACE = 40°
Angle ACE = Angle CED = 40° (Alternate Angles)
If, ABCD is a cyclic quadrilateral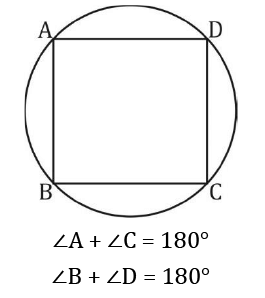 ABCD is a cyclic quadrilateral
ABCD is a cyclic quadrilateral  A tangent at any point of circle is Perpendicular to the radius through the point of contact
A tangent at any point of circle is Perpendicular to the radius through the point of contact OP⊥AB
OP⊥AB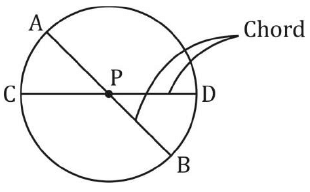 PA × PB = PC × PD
PA × PB = PC × PD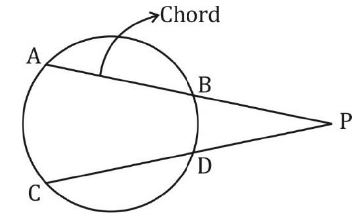
PA × PB = PC × PD
Q1. Chords AB and CD of a circle intersects externally at P. If AB = 6 cm, CD = 3 cm and PD = 5 cm, then the length of PB is?
Sol.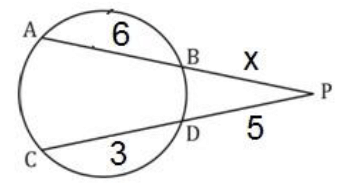 PA × PB = PC × PD
PA × PB = PC × PD
x(6+x)= 5 × 8
x2 + 6x – 40 = 0
x = 4 , -10
PB = 4 PT² = PA × PB
PT² = PA × PB
∠1 = ∠2
AB = CD = Direct Common tangent
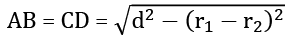
AB = CD Transverse Common Tangents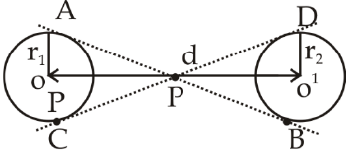
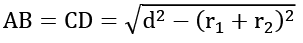
Q1. If the radii of two circles be 6 cm and 3 cm and the length of transverse common tangent be 8 cm, then the distance between the two centers is?
Sol. Length of transverse Common Tangent = 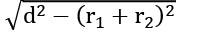

Solved Examples
Q1. In the given figure, O is the centre of the circle and ∠AOB = 75°, then ∠AEB will be?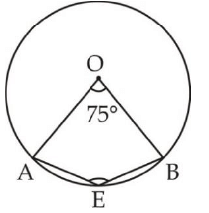 (a) 142.5
(a) 142.5
(b) 162.5
(c) 132.5
(d) 122.5
Sol.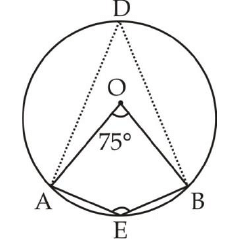 ∠AOB = 75°
∠AOB = 75°
∠ADB =  [Center angle of a circle is twice the angle of the major arc]
[Center angle of a circle is twice the angle of the major arc]
AEBD is a cyclic quadrilateral then,
∠E + ∠D = 180°
∠E + 37.5° = 180°
∠ E = 142.5°
Q2. In a circle, center angle is 120°. Find the ratio of a major angle and minor angle?
(a) 2:7
(b) 2:1
(c) 2:9
(d) 2:3
Sol. 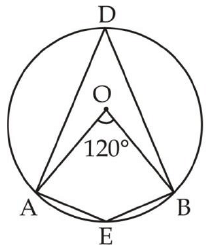
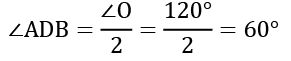
[Center angle of a circle is twice the angle of the major arc]
AEBD is a cyclic quadrilateral then,
∠AEB + ∠ADB = 180°
∠AEB + 180° - 60°
∠AEB = 120°
Required ratio = major angle : minor angle = 120° : 60° = 2 : 1
Q3. A, B & C are three points on a circle such that a tangent touches the circle at A and intersects the extended part of chord BC at D. Find the central angle made by chord BC, if angle CAD = 39°, angle CDA = 41°?
(a) 122
(b) 123
(c) 132
(d) 142
Sol. 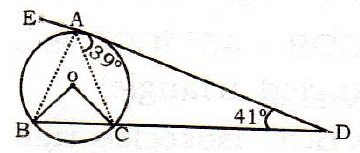 ∠ACB = ∠CAD + ∠CDA [Sum of two interior angle is equal to opposite of exterior angle]
∠ACB = ∠CAD + ∠CDA [Sum of two interior angle is equal to opposite of exterior angle]
∠ACB = 39° + 41° = 80°
∠BAE = ∠BCA = 80°
[Alternate segment]
∠EAB + ∠BAC + ∠CAD = 180°
[Linear angle]
80° + ∠BAC + ∠CAD = 180°
∠BAC = 61°
∴ ∠BOC = 2 × ∠BAC
[Center angle is twice the angle subtended by the major arc]
= 2 × 61° = 122°
Q4. Find the length of the common tangent of two externally touch circle with radius 16 cm and & 9 cm respectively?
(a) 12 cm
(b) 24 cm
(c) 13cm
(d) 28 cm
Sol.  Length of common tangent = (Distance between two circle)²–(Radius1 – Radius2)² AB² = CD² - (16 – 9)²
Length of common tangent = (Distance between two circle)²–(Radius1 – Radius2)² AB² = CD² - (16 – 9)²
AB² = (16+9)² - (7)²
AB² = 625 – 49
AB² = 576
AB = 24 cm
Q5. ABC is an isosceles triangle a circle is such that it passes through vertex C and AB acts as a tangent at D for the same circle. AC and BC intersects the circle at E and F respectively AC = BC = 4 cm and AB = 6 cm. Also, D is the mid-point of AB. What is the ratio of EC : (AE + AD)?
(a) 9:7
(b) 3:4
(c) 4:3
(d) 1:3
Sol.
Here, AC and BC are the secants of the circle and AB is tangent at D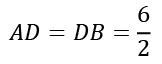
∴ AE × AC = AD²
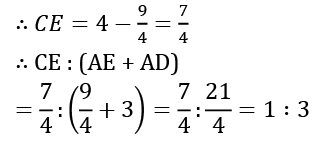
|
314 videos|170 docs|185 tests
|
FAQs on Overview: Circle - Quantitative Aptitude for SSC CGL
| 1. What are the important properties of a circle? |  |
| 2. How is the sector of a circle defined? |  |
| 3. What is the difference between a segment and a sector of a circle? |  |
| 4. How can you calculate the area of a sector of a circle? |  |
| 5. How do you find the length of an arc in a circle? |  |
|
314 videos|170 docs|185 tests
|

|
Explore Courses for SSC CGL exam
|

|

















