Overview: Mathematical Operations | 3 Months Preparation for CAT PDF Download
What are Arithmetic Operations?
Arithmetic operations are techniques for computation that have been used from the dawn to produce precise results for measurements, labeling, and other uses. The word “arithmos,” which merely means “numbers,” is how it got its start in Greek. The fundamental area of mathematics known as arithmetic focuses on the study of numbers and the characteristics of basic mathematical operations including addition, subtraction, multiplication, and division. According to the statement, the four basic operations in arithmetic are addition, subtraction, multiplication, and division.
Fundamental Arithmetical Operations
The four fundamental arithmetic operations are described below:
Addition: A fundamental mathematical operation is addition, which involves finding the sum of two or more numbers or, to put it more simply, adding things. It is represented by the ‘+’ symbol.
- Addition Rules: The operator can be used with decimals, fractions, real numbers, and complex numbers.
Example: If we added 0 to 7, we would still get 7, as the outcome.
0 +7 = 7
If the addition of the opposing value is included in the inverse element. An identity element that is zero is produced when inverse elements are added.
Example: Adding 4 and its opposite – 4
4 + (-4) = 0
Subtraction: The mathematics operation of subtraction demonstrates the difference between two numbers. It is indicated by the minus sign (“-“)
- Subtraction Rules: The difference is positive when the minuend exceeds the subtrahend. It is the opposite of addition.
- Example: 8 -2 = 6
Conversely, if the subtrahend is higher than the minimend, the difference between the two will be negative.
Example: 2 – 8 = -6
Multiplication: The terms multiplicand and multiplier refer to the two values that make up the multiplication operation. It combines two multiplicand and multiplier values to get a single value. It is indicated by the multiply sign ×
- Multiplication Rules: The a.b and a×b form is used to represent the product of two values, denoted a and b.
For example: 8 × 4 = 32
Division: The act of splitting anything into equal pieces or groups is known as division. One of the four fundamental mathematical operations, it yields an equitable result of equal distribution. It is indicated by the multiply sign ÷
- Division Rules: The two values involved are referred to as dividends by the divisor, and if the quotient is larger than 1, the result will be a positive number if the dividend is greater than the divisor.
6 ÷ 2 = 3
Order of Arithmetic Operations
Order of operations refers to the method used to simplify mathematical equations. The order of operations refers to the steps we take to solve a problem, such as adding, subtracting, multiplying, and dividing.
Two terminologies that are used to remember the order of operations are
BODMAS: When a mathematical equation has multiple operations, BODMAS is used. The BODMAS approach has a set of guidelines that must be followed in order. This provides a suitable framework to generate an original response for each mathematical expression.
BODMAS stands for:
- Brackets
- Orders
- Division
- Multiplication
- Addition
- Subtraction
Example: 2 × 20 ÷ 2 + (3 + 4) × 32 − 6 + 15
Step 1: Deal with the brackets to obtain:
2 × 20 ÷ 2 + 7 × 32 – 6 + 15
Step 2: Deal with the Orders to obtain:
2 × 20 ÷ 2 +7 × 9 – 6 +15
Step 3: Since division and multiplication are equivalent operations, combine them from left to right to obtain:
20 + 63 – 6 + 15
Step 4: Deal with them together from left to right to get: Deal with addition and subtraction separately to get: 92
PEMDAS
The PEMDAS rule states that we should solve the operation that occurs first from the left side of the expression when we get to the step of division and multiplication. For both addition and subtraction, the same approach applies: we solve the operation that appears first on the left side.
PEMDAS stands for:
- Parentheses
- Exponents,
- Multiplication,
- Division
- Addition
- Subtraction
Example:
(4 × 3 ÷ 6 + 1) × 32
First, in the given expression, multiply 4 by 3.
(12 ÷ 6 + 1) × 32
Now, inside the bracket, we must divide 12 by 6, giving us,
(2 + 1) × 32
After adding 2 and 1, remove the parentheses.
3 × 32
Simplify the exponent
32 = 3 × 9
3 by 9 multiplied will yield the answer.
3 × 9 = 27
Arithmetic Operations with Whole Numbers
We can simply perform the four fundamental arithmetic operations when working with whole integers. A range of numbers known as whole numbers ranges from 0 to infinity.
On whole numbers, we use basic mathematical operations including addition, subtraction, multiplication, and division.
Addition: The final sum always increases when two or more whole numbers are added.
For example:
If the digits 6, 5, and 8 are added,
6+5+8 = 19
As we can see 19 is greater than the three addends.
Subtraction: When dealing with whole numbers, we always take the lesser of two numbers from the bigger to obtain a difference that is less than the minuend.
For example:
11 – 5 = 6
5 – 11 = -6
Multiplication: When two whole numbers are given, their absolute values are multiplied (or divided), and either a positive or negative sign is written depending on which sign is present.
Example:
3×8=24
−3×−8=−24
Division: When two whole numbers are divided, their absolute values are written with either a positive or negative sign depending on which sign is present.
Example:
27 ÷ (−3) = −9
Arithmetic Operations with Rational Numbers
Rational numbers can be used in arithmetic operations in the same way as whole numbers. The main difference is that rational numbers are represented by the p/q format.
Addition of Rational Numbers: When two rational numbers have the same denominator, addition is achieved by multiplying the numerator terms together while maintaining the same denominator.
Example: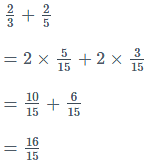
Subtraction of Rational Numbers: Subtracting is adding the additive inverse.
Examples: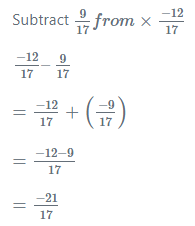
Multiplication of Rational Numbers: The process is the same whether multiplying a proper or improper rational fraction. The procedure entails multiplying and dividing the numerators of both by the sum of their respective denominators.
Example: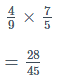
Division of Rational Numbers: The concept of fractional reciprocals is also applied to the division of rational numbers. A given rational number must be multiplied by the reciprocal of the second rational number in order to be divided by another rational number. In other words, division is just multiplication by the divisor’s multiplicative inverse.
For example: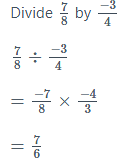
Basic Arithmetic Properties for Real Number
The basic properties of arithmetic are:
Commutative Property
If rearranging the operands has no effect on the outcome, the operation is commutative. Or we may say that adding numbers can be done in any order, and the outcome will remain the same.
This property only applies to addition and multiplication, not division and subtraction.
a + b = b + a
a.b = b. a
For example:
The outcomes will be the same if we add 5 in 2 or 2 in 5.
5+2 = 7 2+5 =7
Associative Property
The order in which the operations are carried out is irrelevant in an expression containing two or more occurrences of only addition or only multiplication as long as the sequence of the operands is kept constant. The term “associative property” refers to this.
a+(b+c)=(a+b)+c
(a.b).c=a.(a.b)
For example:
(6+5)+6=6+(5+6)
17 = 17
As we can see, it gives the same results even when their order is changed.
Distributive Property
Addition and multiplication are combined in the distributive property. If a number multiplies a total enclosed in parenthesis, we can remove the parenthesis by multiplying each term with the same number.
a.(b+c)=a.b+a.c
This characteristic allows us to identify the unknowns and is typically used when an unknown is a component of addition.
Example: Solve this 8×(5+6)
=8×5+8×6
= 40 +48
= 88
Solved Examples of Arithmetic Operations
Example 1: if the sum of the two digits x and a + 5 equals 39. Determine the value of x
Sol: =x+(x+5)=39
= 2x + 5 = 39
Now, Subtracting 5 on both sides,
= 2x + 5 -5 = 39 -5
= 2x = 34
x = 34/2 = 17
The value of x is 17
Example 2: Solve this : 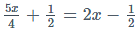
Sol: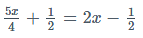
Multiply 4 in both sides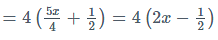
= 5x +2 = 8x -2
= -3x +2 = -2
Now, Subtracting 2 on both sides,
= -3x +2 -2 =-2-2
x = -4/-3
As a result value of x is 4/3
|
284 videos|394 docs|249 tests
|
FAQs on Overview: Mathematical Operations - 3 Months Preparation for CAT
| 1. What is the purpose of the Mathematical Operations CAT exam? |  |
| 2. What topics are covered in the Mathematical Operations CAT exam? |  |
| 3. How long is the Mathematical Operations CAT exam? |  |
| 4. Are calculators allowed in the Mathematical Operations CAT exam? |  |
| 5. How can I prepare for the Mathematical Operations CAT exam? |  |

|
Explore Courses for CAT exam
|

|
















