Overview: Polygons | Quantitative Aptitude for SSC CGL PDF Download
| Table of contents |

|
| What is a Polygon? |

|
| Types of Polygons |

|
| Classification of Polygons |

|
| Polygon Formula |

|
| Sum of Angles in a Polygon |

|
| Solved Examples of Polygons |

|
The polygon is a shape on a flat surface created by straight lines coming together to enclose an area. An example of a polygon is a triangle, which consists of three sides. Polygons are flat shapes in two dimensions. This article explores the concept of polygons in mathematics, focusing on types such as triangles—equilateral, isosceles, scalene, and right-angledtriangles—and quadrilaterals like parallelograms, rectangles, squares, rhombuses, and trapeziums. It discusses formulas for calculating area, perimeter, the total of exterior angles, and the sum of interior angles, accompanied by solved examples and detailed illustration.
What is a Polygon?
It's a flat shape with many sides. Each type has a name based on its number of sides. For instance, a triangle (3-gon) has three sides, and a quadrilateral (4-gon) has four sides. There are many other types based on the number of sides.
Polygon Definition
- Polygons: Two-dimensional shapes with sides and angles at their corners.
- Not All 2D Shapes are Polygons: While polygons have sides and angles, not all 2D shapes do.
- Definition of Sides/Edges: Line segments that form the boundaries of a polygon.
- Vertices/Corners: The points where two sides of a polygon meet, creating angles.
- Non-Polygon Example: Circles, despite being 2D, are not polygons due to their lack of sides and angles.
Types of Polygons
Well acknowledged with the definition, let us take a step forward with the various types and learn about them.
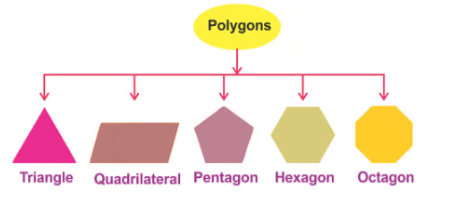
Triangles (3 Sided Polygon)
One of the basic properties of a triangle is that the total sum of the internal angle of a triangle is equal to 180 degrees and depending on the sides, angles and vertices they are classified as follows:
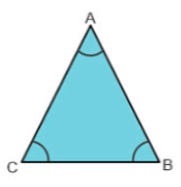
Equilateral TriangleA triangle with all the sides equal is called an equilateral triangle. Consider, ∆ABC; for the triangle to be an equilateral triangle the condition of the sides is; AB = BC = CA, and each angle should be equal to 60 degrees that is ∠A = ∠B = ∠C = 60°.
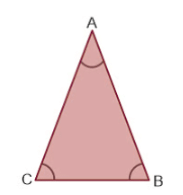
Isosceles Triangle
A triangle is termed an isosceles triangle whose two sides are equal. Consider a ∆ABC is an isosceles triangle then AB = AC in addition to this angles opposite to equal sides are equal i.e. in the figure shown below ∠B = ∠C.
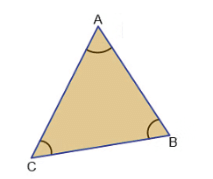
Scalene Triangle
A triangle whose all three sides are different or unequal in length is called a scalene triangle.
Right Angle Triangle
A triangle whose one angle is 90° is called a right-angled triangle. Here, ∆ABC is a right-angled triangle because ∠C = 90°.
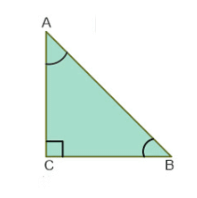
- Triangles can be classified based on their angles into acute-angled triangles (with angles less than 90°) and obtuse-angled triangles (with an angle greater than 90°).
- This classification will be covered in detail in a separate article on triangles.
Quadrilateral (4 Sided Polygon)
Any four non-collinear points form a quadrilateral; the quadrilateral has multiple names depending on the shape. Some of the important ones are discussed below:
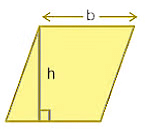
Parallelogram
In a parallelogram figure, opposite sides are parallel and identical with diagonals bisecting each other. Also, the summation of two adjacent angles is 180 degrees.
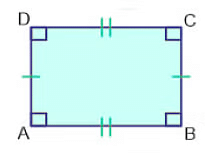
Rectangle
In a rectangle, opposite sides are parallel and equivalent with diagonals bisecting each other. Also, all the angles in a rectangle are equal and the summation of the adjacent angles is equal to 180 degrees.
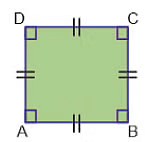
Square
In a square all the four sides are equal and the opposite side is parallel to one another with diagonals bisecting each other. Along with this, all the angles are of the same measure i.e. 90 degrees.
Rhombus
In a rhombus all the four sides are equal and the opposite side is parallel to one another with diagonals bisecting one another. The measures of the angles are different but the opposite angles are equal.
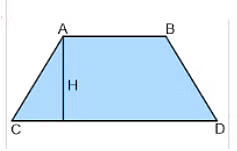
Trapezium
In a trapezium, all sides are of different lengths in such a way that one pair of opposite sides is parallel. There is nothing certain about the angles, or diagonals of a trapezium.
Other Polygons
Some other significant examples of polygons are as follows:- Pentagon: A shape with five straight lines and angles of 108 degrees.
- Hexagon: A figure with six sides and angles measuring 120 degrees.
- Heptagon: A polygon having seven sides.
- Octagon: A polygon with eight sides.
- Nonagon: A nine-sided shape.
- Decagon: A polygon featuring ten sides.
- Hendecagon: An eleven-sided figure.
- Dodecagon: A shape with twelve sides
Classification of Polygons
Now that we know the definition along with the types and their details, let us now learn the classification for the same.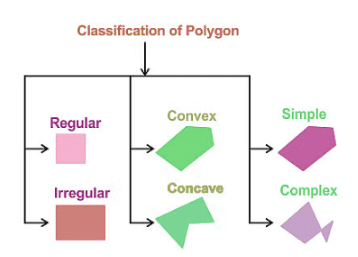
Regular and Irregular
- Regular Polygon: A regular polygon has all sides and interior angles that are equal, like a rhombus, square, or equilateral triangle.
- Irregular Polygon: An irregular polygon has unequal sides and angles, such as a rectangle, a scalene triangle, or a kite.
Concave or Convex
- A shape with all its inside angles less than 180 degrees is known as a convex polygon. On the other hand, if any inside angle is more than 180 degrees, it is termed a concave polygon.
Simple or Complex
- A simple type of polygon contains only one boundary, where the lines or sides do not cross over themselves.
- In contrast, in a complex type of polygon, the sides intersect each other
Polygon Formula
Area and Perimeter of Polygons
The perimeter can be understood as the total distance surrounded by the border of any two-dimensional shape. The perimeter of some regularly used polygons are listed below:
- The perimeter of a triangle is simply the entire length of the outer boundary of the triangle that is equal to; Total sum of all Sides.
- The perimeter of the parallelogram = 2 × (sum of lengths of adjacent sides).
- Perimeter of the square = 4a (a=side length).
- The perimeter of a rhombus =4x (x=side length)
- Perimeter of a rectangle = 2 x (L + B)
The area is the total room occupied by them. The area of the polygon formula depends upon the number of sides and the classification as well. The area formula for some commonly used shapes are:
- Area of triangle =1/2 × Base × Height.
- Area of the parallelogram = (base x height).
- Area of the square= a2.
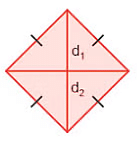
- The area of a rhombus =12×d1×d2. Here d1 and d2 are the length of two diagonals of the rhombus.
- Area of a rectangle = Length × Breadth.
Sum of Angles in a Polygon
In the previous heading, we learnt about the various area and perimeter-related formulas, continuing the same let us learn about the summation of angles. The angles are classified into interior angles and exterior angles for different types of polygons.
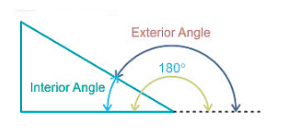
Sum of Interior Angles of a Polygon
The interior angles as the name suggests are the angles formed between the adjacent sides inside the polygon. These angles are equal in the case of a regular polygon.
- The sum of all the interior angles of n side regular polygon = (n − 2) × 180°= (n − 2)π radians Where ‘n’ denotes the sides of a polygon.
- For a regular polygon each internal angle= (n−2)×180°/n
Sum of Exterior Angles of a Polygon
An exterior angle as per the name is the angle between any side of a given shape and a line stretched(clockwise or anticlockwise) from the next side.
- For an ‘n’ side regular polygon the sum of all external angle= 360°
- Hence, each exterior angle=360°/n
- For a regular polygon external angle + Internal angle = 180°
Solved Examples of Polygons
Example 1: A quadrilateral with four sides the sum of all the interior angles is?
 View Answer
View Answer 
= (4 – 2) × 180°
= 2 × 180°
= 360°
 View Answer
View Answer 
Assume the exterior and interior angle of a polygon as 2x and 3x.
2x + 3x = 180°
5x = 180°
x = 36°
Exterior angle = 72°
number of sides = 360°/exterior angle
= 360°/72°
= 5
A polygon shape with 5 sides is the pentagon.
 View Answer
View Answer 
Given that:
180(n – 2) = 540
n – 2 = 3
n = 5
The number of sides= 5.
 View Answer
View Answer 
As per the formula, each exterior angle=360°/n
Here n=number sides.
60°=360°/n
n=360°/60°
n=6
The polygon is a Hexagon.
|
315 videos|290 docs|185 tests
|















